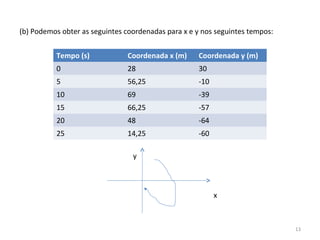
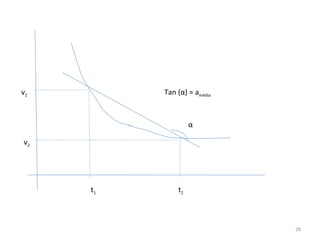
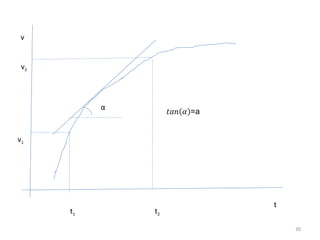
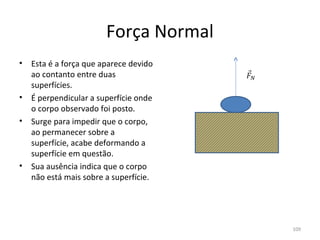
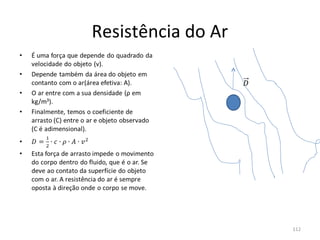
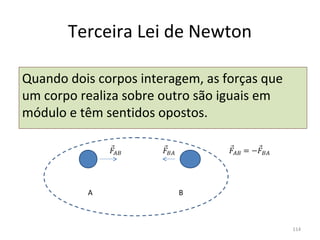
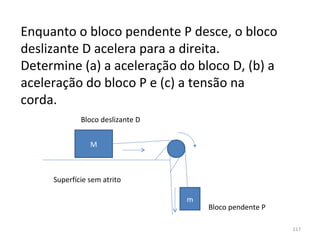
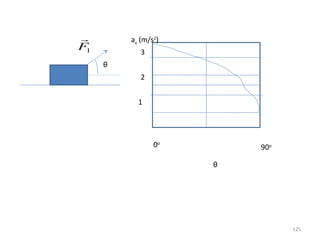
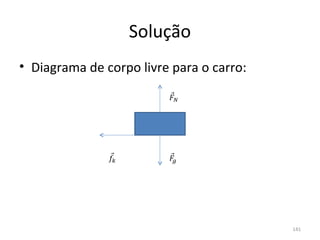
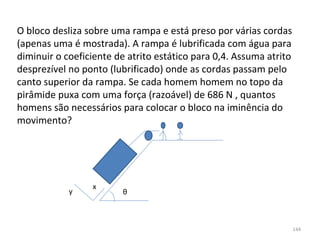
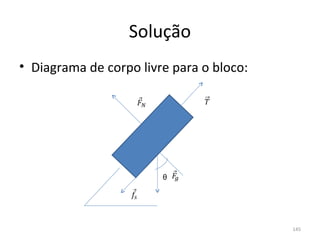
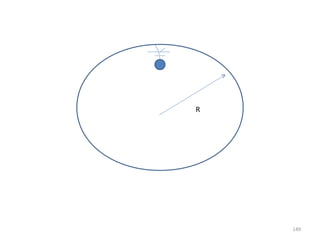
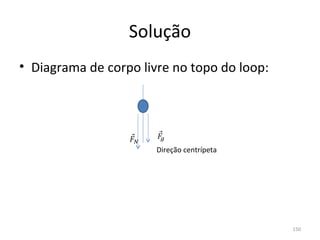
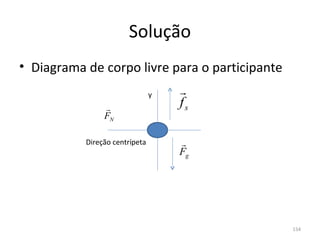
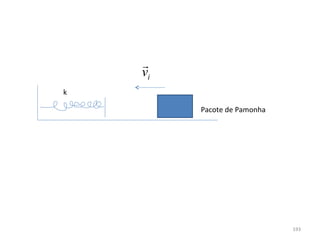
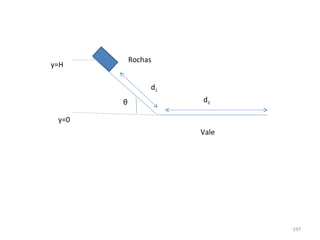
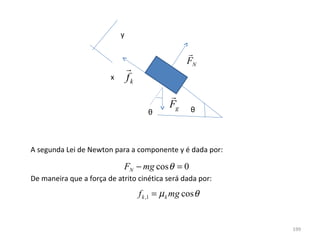
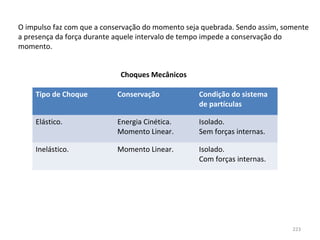
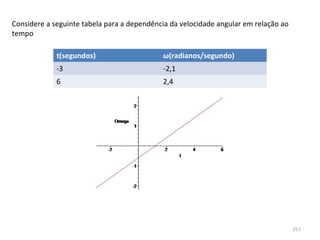
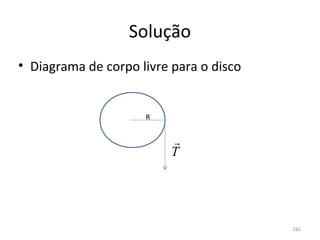
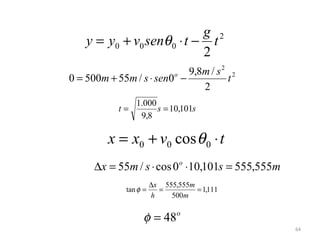O gráfico mostra que a velocidade da partícula varia linearmente com a posição x. Isso significa que a aceleração é constante. Para encontrar o valor da aceleração, basta calcular a inclinação da reta, que é dada pela variação de velocidade dividida pela variação de posição. Neste caso, a variação de velocidade é de 6 m/s e a variação de posição é de 4 m. Logo, a aceleração é de 6/4 = 1,5 m/s2. Conclusão: a aceleração é constante

1. Universidade Federal Rural de Pernambuco
Unidade Acadêmica de Serra Talhada
Curso: Agronomia
Disciplina: Física do Ambiente Agrícola
Professor: Mário Oliveira
Data: 15 /08/2011
1

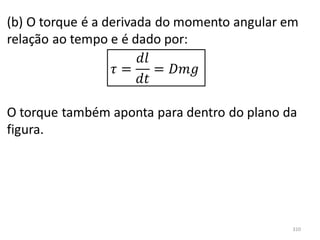
2. Notas
1 
• Aprovação Qualificada: .. − 3 
1 V . A. + 2 V . A  a a a
V . A. ≥ 7,0
2     
  
 2 / 5+3 / 5 2 / 5+ 3 / 5  
2
[(1 V .A. + 2 V .A.) − 3 V .A.] ≥ 3,0
1
• Aprovação Simples: se , pode-se fazer a final:
a a a
2 2
[ a a
]
 (1 V . A. + 2 V . A.) − 3 V . A. + V . A.Final  ≥ 5,0
1 1 a 

• A primeira e a segunda verificação serão divididas em duas partes.
A primeira parte com 4,0 pontos e a segunda parte com 6,0 pontos.
• Primeira V.A. : 09/05/2011 e 12/05/2011
• Segunda V.A.: 16/06/2011 e 20/06/2011
• Terceira V.A.: 07/07/2011
• V.A. Final: 18/07/2011
• Aulas extras: 24/03/2011 (Sala 01 Bloco 03 08:00-10:00), 14/04/2011 (Sala 01 Bloco 03 08:00-
10:00), 19/05/2011 (Sala 02 Bloco 03 08:00-10:00), 26/05/2011 (Sala 01 Bloco 03 08:00-
10:00), 02/06/2011(Sala 01 Bloco 03 08:00-10:00)
2

3. Faltas
• 25% é o limite máximo.
• O número máximo de faltas é 19.
Listas de Exercícios
https://sites.google.com/site/ensinodefisicanauast/home/listas-de-exercicios
Gabaritos
https://sites.google.com/site/ensinodefisicanauast/home/gabaritos
3

4. Bibliografia
• Fundamentos de Física I,II, IV Halliday e
Resnick. Editora L.T.C., 2009, 8a ed..
• Física I, Sears e Zemansky, Addison Wesley,
2006, 10a ed.
• Física, Volume 1, Paul A. Tipler, Gene Mosca,
Editora L.T.C., 2006, 5a ed.
4

5. Física do Ambiente Agrícola
Turma: SA3
Código da Disciplina: FISC5002
5

6. Movimento Retilíneo
Unidade I
6

7. Movimento
• Quando um objeto ocupa lugares diferentes em
tempos diferentes, dizemos que ele está em
movimento.
• O movimento mais simples é aquele que
acontece sobre uma linha reta. Para simplificar
ainda mais, vamos considerar o objeto como um
ponto: ponto material (ponto dotado de massa).
• O movimento retilíneo (sobre uma linha reta) é o
que vamos tratar no início.
7

8. Posição e Deslocamento
• Posição é uma coordenada do referencial do observador,
representada por um vetor que aponta da origem (onde está
o observador) até o objeto que estamos estudando
(partícula).
• É a trilha deixada pela partícula quando se move de uma
posição para outra.
∆x = x2 − x1 Deslocamento 1-D
  
∆r = r2 − r1 Deslocamento 2-D ou 3-D
• Sua unidade no S.I. é o metro.
8

9. Exemplo 4-1
9

10. Solução
10

11. Exemplo 4-2
11

12. Solução
12

13. (b) Podemos obter as seguintes coordenadas para x e y nos seguintes tempos:
Tempo (s) Coordenada x (m) Coordenada y (m)
0 28 30
5 56,25 -10
10 69 -39
15 66,25 -57
20 48 -64
25 14,25 -60
y
x
13

14. Velocidade Média
• Velocidade média é a medida da rapidez de
uma partícula em um intervalo de tempo. É
obtida através da inclinação da secante que
une dois pontos no gráfico da posição em
função do tempo. Unidade do S.I.: m/s.
∆x x futuro − x passado
vmédia = =
∆t t futuro − t passado
Velocidade média 1-D
  
 ∆r r futuro − rpassado
vmédia = =
∆t t futuro − t passado
Velocidade média 2-D ou 3-D 14

15. A velocidade média faz parte da secante à trajetória da partícula.
x
x2
tan ( α ) = vmédia
α
x1
t1 t2 t
15

16. Velocidade Escalar Média
• A velocidade escalar média mede a rapidez,
mas sem considerar o sentido ou a direção do
deslocamento.
• É definida com a razão entre a distância
percorrida pelo intervalo de tempo gasto no
percurso:
Distância percorrida
smédia =
∆t
16

17. Exemplo 2-1
• Você dirige uma picape ao longo de uma estrada retilínea por 8,4 km a 70
km/h, quando ela para por falta de gasolina. Nos próximos 30 minutos,
você caminha ao longo da estrada na direção de um posto de gasolina.
• (a) Qual o deslocamento desde do início da viagem até a chegada ao
posto de gasolina?
• (b) Qual é o intervalo de tempo desde do início da viagem até a chegada
ao posto de gasolina?
• (c) Qual é a velocidade média do começo da viagem até a chegada ao
posto de gasolina? Encontre-a numericamente e graficamente.
• (d) Suponha que para pegar a gasolina, pagar e voltar até o carro; você
gaste 45 minutos. Qual é a velocidade escalar média desde do começo da
viagem até a volta até o carro
17

18. Solução
18

19. 10,4
8,4
19

20. Velocidade instantânea
• Quando desejamos analisar a rapidez em um
instante de tempo, usamos a velocidade instantânea.
Ela é dada pela derivada da posição em relação ao
tempo ou pela inclinação da tangente no gráfico da
posição em função do tempo. Unidade do S.I.: m/s.
dx ∆x
v= = lim
dt ∆t →0 ∆t
Velocidade instantânea 1-D
 
 dr ∆r dx ˆ dy ˆ
v= = lim = i+ j
dt ∆t →0 ∆t dt dt
Velocidade instantânea 2-D
20

21. x
x2
α
Tan(α)=v
x1
t2
t1 t
A velocidade instantânea faz parte da tangente à trajetória da partícula.
21

22. Velocidade Escalar
• A velocidade escalar instantânea é o módulo
da velocidade instantânea:

s= v
22

23. Exemplo 2-3
• A posição de uma partícula se movendo em
um eixo x é dada por:
• x=7,8+9,2t-2,1t3
• Com x em metros e t em segundos. Qual é a
velocidade em t= 3,5 s? A velocidade é
constante ou está variando continuamente?
23

24. Solução
24

25. Exemplo 4-3
• Para o coelho do Exemplo 4-2, encontre a
velocidade no tempo t=15 s.
25

26. Solução
26

27. Aceleração
• A aceleração média mede o avanço ou recuo da
velocidade em um intervalo de tempo. É dada
pela inclinação da secante em um gráfico de
velocidade contra tempo. Unidade do S.I.: m/s2
∆v v2 − v1
a= =
∆t t 2 − t1
Aceleração média 1-D
  
 ∆v v2 − v1 ∆v x ˆ ∆v y ˆ
a= = = i+ j
∆t t 2 − t1 ∆t ∆t
Aceleração média 2-D
27

28. v1 Tan (α) = amédia
α
v2
t1 t2
28

29. Aceleração Instantânea
• A aceleração instantânea é a medida do
avanço ou do recuo da velocidade em certo
instante de tempo. Unidade do S.I.: m/s2
dv ∆v
a= = lim
dt ∆t →0 ∆t
Aceleração instantânea 1-D
 
 dv ∆v dv x ˆ dv y ˆ
a= = lim = i+ j
dt ∆t →0 ∆t dt dt
Aceleração instantânea 2-D
29

30. v
v2
α
v1
t
t1 t2
30

31. Exemplo 2-4
31

32. Solução
32

33. Exemplo 4-4
• Para o coelho do Exemplo 4-2 e 4-3, encontre
a aceleração do coelho para t=15s.
33

34. Solução
Θ=145o
34

35. Aceleração Constante
Velocidade inicial.
Posição inicial.
Velocidade inicial.
35

36. Equação de Torricelli
Velocidade inicial
Posição inicial
36

37. Exemplo 2-5
• A cabeça de um pica-pau está se movendo
para frente com uma velocidade de 7,49 m/s
até o bico encontrar o tronco da árvore. O
bico para depois de penetrar o tronco em 1,87
mm. Assuma que a aceleração é constante,
encontre o módulo da aceleração em
unidades de g.
37

38. Solução
38

39. Exemplo 2-6
• A Figura abaixo mostra o gráfico da velocidade
v da partícula contra a posição, quando a
partícula se move ao longo do eixo x com
aceleração constante. Qual é a velocidade da
partícula em x=0?
v (m/s)
20
8 70 x(m)
39

40. Solução
50
40

41. 41

42. Exemplo 4-5
42

43. Solução
43

44. Queda livre
• Queda livre é quando a partícula, que está sendo estudada, se
move somente pela influência da gravidade da Terra.
• Supondo o ar rarefeito, podemos considerar o movimento
nas proximidades da superfície da Terra com uma queda livre.
• Próximo ao nível do mar e para regiões planas (planícies e
planaltos), podemos dizer que a gravidade da Terra impõe
que os objetos se movam com aceleração constante para
baixo e de módulo constante igual a g=9,8 m/s2.
44

45. 45

46. Exemplo 2-7
• Em 26 de setembro de 1993, Dave Munday foi para o lado canadense das
Cataratas do Niágara equipado com uma bola de aço com um furo de ar
para entrada de ar e caiu 48m na direção da água (e das rochas). Assuma
que a velocidade inicial foi zero, e despreze a resistência do ar.
• (a) Quanto durou a queda de Munday até atingir a superfície da água?
• (b) Munday conseguia contar três segundos até a queda, mas não podia
ver o quanto ele tinha caído a cada segundo. Determine a sua posição no
final de cada segundo.
• (c) Qual era a velocidade de Munday quando ele atingiu a superfície da
água?
• (d) Qual era a velocidade de Munday no final de cada segundo? Ele podia
perceber o aumento da velocidade?
46

47. Solução
47

48. Tempo(segundo) Posição(metro)
0s 48m
1s 43,1m
2s 28,4m
3s 3,9m
48

49. 49

50. Tempo Velocidade
(segundo) (m/s)
0 0
1 -9,8
2 -19,6
3 -29,4
proporcionais e é difícil distinguir um do outro.
50

51. Exemplo 2-8
• Na figura abaixo, um jogador joga uma bola
de beisebol para cima com um velocidade de
12 m/s ao longo do eixo y.
y
• (a) Quanto tempo a bola leva para chegar na
sua altura máxima?
51

52. (b) Qual é a altura máxima da bola em
relação ao seu ponto de partida?
(c) Quanto tempo a bola leva para
atingir a altura de 5m em relação ao
seu ponto de partida?
52

53. Solução
• (a) A altura máxima ocorrerá quando a
velocidade da bola for nula, pois ela deve
parar de subir. Substituindo essa condição na
equação para a velocidade em função do
tempo:
v = v0 − gt 0 = 12m / s − 9,8m / s t
2 t=
12
9,8
s = 1,224 s
• (b) Podemos obter a altura máxima usando a
equação da posição em função do tempo:
53

54. g 2
y = y0 + v0t − t
2
9,8m / s 2
y = 0 + 12m / s1,224 s − (1,224s ) 2 = 7,348m
2
(c) A equação da posição em função do tempo
pode fornecer o tempo necessário para que a bola
atinja 5m de altura:
g 2 5m = 0 + 12m / st − 9,8m / s 2 t 2
y = y0 + v0t − t 2
2
54

55. 2
 t   t 
− 4,9
 seg.  + 12 seg .  − 5 = 0
  
   
− 12 ± 144 − 4 ⋅ ( − 4,9 ) ⋅ ( − 5)  12 6,782 
t= seg. =    seg .
2 ⋅ (−4,9)  9,8 9,8 
t = 0,532 seg ou t = 1,916 seg
55

56. Movimento em Duas e Três
Dimensões
Unidade II
56

57. Movimento de Projéteis
• Quando lançamos objetos e os deixamos somente
sobre a influência da gravidade da Terra, temos um
movimento balístico. A partícula estudada é tida
como um projétil.
• Considere a componente horizontal da posição como
x e a componente vertical como y.
• O ângulo da velocidade inicial com o eixo x é o
ângulo de lançamento do projétil.
57

58. y
O movimento horizontal é independente do movimento vertical.
O movimento horizontal tem velocidade constante, enquanto o
Movimento vertical possui aceleração constante.
θ0
x
58

59. 59

60. Equação de Torricelli:
v y = v0, y − 2 ⋅ g ⋅ ( y − y0 )
2 2
Eliminando o tempo através do uso da equação para a componente horizontal da
posição, podemos obter a equação que determina a forma geométrica da trajetória:
2
g  x − x0 
y = y0 + tan (θ 0 )( x − x0 ) −  v cos(θ ) 

(*
2 0 0  )
Percebemos que sem a presença da gravidade da Terra (g=0), o projétil seguiria
uma linha reta. Entretanto, a trajetória é parabólica. A parábola possui
concavidade para baixo e cresce sua concavidade com o aumento da velocidade
inicial e da aceleração da gravidade.
60

61. Exemplo 4-6
• Na Figura abaixo, um avião de resgate voa à
198 km/h (=55 m/s) e uma altura constante de
500 m dirigindo-se a um ponto diretamente
sobre a vítima, onde uma balsa deve ser
lançada.
h
61

62. (a)Qual deve ser o ângulo da linha de
visada do piloto até a vítima, onde a
balsa deve chegar?
(b)Quando a cápsula atinge a água,
qual deve ser sua velocidade em
termos de vetores unitários e na
notação módulo e ângulo ?
62

63. Solução
• (a) O ângulo da linha de visada é oposto ao
deslocamento horizontal do avião e adjacente
à altura do avião, sua tangente é dada pela
razão do deslocamento horizontal pela altura
do avião. O deslocamento horizontal pode ser
calculado através do uso da equação da
componente vertical da posição (para
encontrar o tempo) e da componente
horizontal (para encontrar o deslocamento):
63

64. g 2
y = y0 + v0 senθ 0 ⋅ t − t
2
9,8m / s 2 2
0 = 500m + 55m / s ⋅ sen0o − t
2
1.000
t= s = 10,101s
9,8
x = x0 + v0 cos θ 0 ⋅ t
∆x = 55m / s ⋅ cos 0o ⋅10,101s = 555,555m
∆x 555,555m
tan φ = = = 1,111
h 500m
φ = 48o
64

65. (b) A equação para a velocidade em função do tempo
possui duas componentes. A componente horizontal é
constante e a componente vertical varia linearmente
com o tempo:
v x = v0 ⋅ cos θ 0 = 55m / s ⋅ cos 0o = 55m / s
v y = v0 senθ 0 − g ⋅ t
v y = 55m / s ⋅ sen0o − 9,8m / s 2 ⋅10,101s = −98,990m / s

v = ( 55m / s ) i + ( − 98,990m / s ) ˆ
ˆ j
v=113,243m / s e θ =− ,943o
60
65

66. Exemplo 4-7
66

67. (b) Qual é o alcance máximo
das balas de canhão ?
67

68. Solução
• (a) Podemos obter o alcance das balas de
canhão com o uso combinado das equações
para a componente horizontal em função do
tempo e da componente vertical em função
do tempo. A componente vertical em função
do tempo permite obter o tempo de voo da
bala de canhão:
68

69. 69

70. 70

71. Movimento Circular Uniforme
• Quando uma partícula possui um trajetória em forma de
círculo dizemos que seu movimento é circular.
• Se o movimento é realizado percorrendo deslocamentos
angulares proporcionais aos tempos gastos para realizá-los,
temos um movimento circular uniforme.
• O movimento circular é periódico, devido à forma do fechada
do círculo.
• O movimento circular sendo não-reto possui aceleração.
Apesar disso o M.C.U. (movimento circular uniforme) possui
velocidade de módulo constante (e direção, sentido variáveis)
71

72. y 
v
R 
r
θ
x
Partícula se movendo em movimento circular uniforme.
72

73. Para um observador no centro do círculo, temos para um movimento circular
uniforme com raio R e período T:
i)Componente x da posição:
x = ⋅

R cos
2 t 

π
 T 
ii) Componente y da posição:
 2πt 
y = R ⋅ sen 
 T 
Esse resultado vem da decomposição do vetor posição em coordenadas
cartesianas e da proporção existente entre o ângulo percorrido e o tempo
gasto para atingir esse ângulo.
73

74. Para obter a velocidade, basta efetuar a derivada da posição em relação ao tempo.
Componente x da velocidade:
2πR  2πt 
vx = − ⋅ sen 
T  T 
Componente y da velocidade:
2πR  2πt 
vy = ⋅ cos 
T  T 
Fazendo o produto escalar com o vetor posição, observamos que o mesmo é nulo.
Portanto, o vetor posição e a velocidade são perpendiculares. Um resultado esperado,
pois a velocidade faz parte da tangente ao círculo. O módulo da velocidade é dado por:
2πR
v= ,
T
Comprimento do círculo dividido pelo período.
74

75. A aceleração pode ser obtida como derivada da velocidade em relação ao tempo:
Componente x da aceleração:
v2  2πt 
a x = − ⋅ cos 
R  T 
Componente y da aceleração:
v2  2πt 
a y = − ⋅ sen 
R  T 
A aceleração é centrípeta (aponta para o centro do círculo):
 2
 v r
a=−
R R
O módulo é dado por:
v2
a=
R
75

76. A frequência do movimento circular uniforme é dada por (unidade do S.I. é o
hertz):
1
f =
T
A velocidade angular do movimento circular uniforme é dada por (unidade do
S.I. é rad/s) :
v
ω = 2πf =
R
76

77. Exemplo 4-10
• Pilotos de caça sempre se preocuparam em
fazer uma volta muito fechada. Quando o
piloto sofre os efeitos da aceleração
centrípeta, com a cabeça ao longo do centro
de curvatura, a pressão sanguínea no cérebro
decresce, levando à perda das funções
cerebrais. Há vários sinais de aviso. Quando a
aceleração centrípeta é 2g ou 3g, o piloto se
sente pesado.
77

78. 78

79. Solução
• Como a velocidade muda de sentido durante
o loop, temos que o loop corresponde a um
semicírculo. Sendo assim, o tempo do loop
corresponde a um meio período e o período
do M.C.U. é portanto T=48s. Com o período
podemos obter o raio da trajetória, mas antes
devemos calcular a velocidade escalar:
79

80. 80

81. Movimento Relativo
• As medidas feitas por um observador são, em
princípio, diferentes das realizadas por outro
observador.
• Considere a relatividade de Galileu, onde
temos observadores que se separam um do
outro através de uma velocidade constante.
• Temos o observador A (Alex) em repouso sobre o solo e o referencial
B(Bárbara) em movimento com velocidade constante, em linha reta
horizontal, em relação à Alex (ou ao solo).
81

82. Dois Referenciais de Galileu
Alex Bárbara
Objeto
xOA xOB
VBA
82

83. Transformações de Galileu
 xOB = xOA − vBA ⋅ tOA

tOB = tOA
Dicionário das posições e tempos
vOB = vOA − vBA
Dicionário de velocidades
83

84. Invariantes
• Tempo (tempo absoluto).
• Aceleração.
• Força.
• Qualquer lei física, e em especial,as fórmulas
que representam a lei física.
Um referencial de Galileu é
conhecido como referencial inercial,
pois deixa as leis de Newton
invariantes.
84

85. Exemplo 4-11
85

86. 86

87. Solução
87

88. 88

89. Relatividade 2-D
Objeto
 
rOA rOB

vBA Bárbara
Alex
89

90. Transformações de Galileu
  
rOB = rOA − vBA ⋅ tOA

tOB = tOA
Dicionário das posições e tempos.
  
vOB = vOA − vBA
Dicionário de velocidades.
Um referencial que não obedece à relatividade de
Galileu é conhecido como referencial não-inercial.
(Por exemplo, um observador girando em torno de
um eixo fixo no espaço).
90

91. Exemplo 4-12
91

92. N
20o
L
92

93. Solução
93

94. 94

95. Força e Movimento
Unidade III
95

96. Primeira Lei de Newton
96

97. • A primeira Lei de Newton supõe que o observador é inercial (obedece à
relatividade de Galileu), e portanto, admite que um observador que se move
com velocidade constante em relação à ele é equivalente a esse observador
em questão.
• Um observador inercial sempre garante que na ausência de forças temos que a
partícula observada se move em linha reta com velocidade constante (M.R.U.)
ou permanece em repouso.
• Dessa forma, na ausência de forças a partícula está em equilíbrio. Este
equilíbrio pode ser estático, se tivermos repouso (ausência de movimento); ou
dinâmico, se tivermos um movimento retilíneo uniforme.
• Um corpo em M.R.U. ou repouso está inerte do ponto de vista da dinâmica.
• Quanto mais massa (quantidade de matéria) um corpo tiver, maior será a sua
inércia (tendência a permanecer em equilíbrio).
• As outras leis de Newton também exigem que o observador seja inercial.
• Força é a causa unidimensional do movimento (puxar, empurrar, etc.)
• Força resultante é a soma vetorial de todas as forças.
• O efeito combinado de um conjunto de forças é dado pela força resultante.
97

98. Segunda Lei de Newton
A força resultante que age sobre um corpo é
dada pelo produto da massa do corpo por sua
aceleração.
Unidade de Força no S.I.: Newton (N).
Unidade de massa no S.I.: quilograma (kg)
98

99. • Devemos fazer um diagrama de corpo livre isolando as forças que atuam sobre o
corpo observado.
• Em seguida, devemos somar as forças que atuam sobre o corpo; obtendo a força
resultante.
• Resta obter massa ou aceleração do corpo, em questão, dependendo das medidas
feitas ou dos dados fornecidos.
• A segunda lei de Newton propõe que o fator entre força (causa do movimento) e
aceleração (efeito do movimento) é a massa. Por isso a massa é conhecida como a
inércia do corpo (em coordenadas cartesianas).
• Quanto maior a massa, menor será a aceleração adquirida pelo corpo.
• Quanto maior a força, maior será a aceleração adquirida pelo corpo.
99

100. Exemplo 5-3
100

101. (A) (B) (C)
101

102. Solução
102

103. 103

104. Exemplo 5-2
• Na vista superior da Figura, uma lata de
biscoitos de 2kg é acelerada a 3m/s2 na

orientação definida por , em uma superfície
a
horizontal sem atrito. A aceleração é causada
por três forças horizontais, das quais apenas
 
F2
duas são mostradas; , de módulo 10N e ,
F1

de módulo 20N. Qual é a terceira força, ,
F3
em termos dos vetores unitários e na notação
módulo-ângulo?
104

105. y

F2 
a
50o
30o x

F1
105

106. Solução
• A segunda lei de Newton para o problema diz
que a soma das três forças é igual ao produto
da massa pela aceleração. Esta equação
vetorial corresponde a duas equações
escalares:
 F1, x + F2, x + F3, x = ma x − F1 cos 300 + 0 + F3, x = ma cos 50o

 
− F1sen30 + F2 + F3, y = masen50
0 o
 F1, y + F2, y + F3, y = ma y 


m
− 10 N cos 30o + F3, x = 2kg ⋅ 3 2 ⋅ cos 50 o  F3, x = 12,5 N

s 
m
− 10 Nsen30o + 20 N + F3, y = 2kg ⋅ 3 2 ⋅ sen50o  F3, y = −10,4 N
 s
106

107. Em coordenadas cartesianas, a terceira
força vale:

F3 = (12,5 N ) i + ( − 10,4 N ) ˆ
ˆ j
Para obter a força em coordenadas polares,
devemos calcular o módulo da força e o ângulo
que ela faz com o eixo x:
F3 = F32x + F32y
, , F3 = 16 N
F3, y
tan θ = θ = −40 o
F3, x
107

108. Força Gravitacional
Terra
108

109. Força Normal
• Esta é a força que aparece devido
ao contanto entre duas
superfícies.
• É perpendicular a superfície onde
o corpo observado foi posto.
• Surge para impedir que o corpo,
ao permanecer sobre a
superfície, acabe deformando a
superfície em questão.
• Sua ausência indica que o corpo
não está mais sobre a superfície.
109

110. Força Elástica
A força elástica é sempre
oposta ao deslocamento, de
maneira a garantir o retorno
da mola à sua posição de
equilíbrio.
110

111. Tensão (Tração)
• Quando prendemos
uma corda a um objeto,
a corda realiza uma
força conhecida como
tensão da corda;
fazendo o objeto se
mover.
• Essa força aponta do
objeto para a corda.
111

112. Resistência do Ar
112

113. 113

114. Terceira Lei de Newton
Quando dois corpos interagem, as forças que
um corpo realiza sobre outro são iguais em
módulo e têm sentidos opostos.
A B
114

115. A terceira lei de Newton nos diz como um sistema mecânico se forma.
O sistema se forma aos pares como um corpo agindo (ação) e outro
reagindo (reação), com forças opostas.
Existem duas versões da terceira lei:
Fraca: o par de forças (ação e reação) são opostos, mas não estão na
linha que une os corpos.
Forte: o par de força (ação e reação) são opostos e estão na linha que
une os corpos.
A terceira lei de Newton é uma expressão da conservação do momento.
Um dos princípios mais queridos da Física.
115

116. Exemplo 5-4
• A Figura mostra um bloco D (o bloco
deslizante) de massa M=3,3 kg. O bloco está
livre para se mover ao longo de uma
superfície horizontal sem atrito e está ligado,
por uma corda que passa por uma polia sem
atrito, a um segundo bloco P (o bloco
pendente), de massa m=2,1 kg. As massas da
corda e da polia podem ser desprezadas em
comparação com a massa dos blocos.
116

117. Enquanto o bloco pendente P desce, o bloco
deslizante D acelera para a direita.
Determine (a) a aceleração do bloco D, (b) a
aceleração do bloco P e (c) a tensão na
corda.
Bloco deslizante D
M
Superfície sem atrito
m
Bloco pendente P
117

118. Solução
• Diagrama de corpo livre para o bloco D:

FN 
T

Fg
• Diagrama de corpo livre para o bloco P:

FN

Fg 118

119. A segunda lei de Newton para o bloco D é dada por (esquecendo o movimento na
direção vertical):
T = Ma (I )
A segunda lei de Newton para o bloco P é dada por:
T − mg = m( − a ) (II )
Subtraindo a equação (II) da equação (I), podemos obter o módulo da aceleração dos
dois blocos (eles têm o mesmo módulo de aceleração, pois estão unidos por uma corda
e perfazem o mesmo deslocamento em um dado intervalo de tempo):
m m
a= g = 3,8 2
M +m s
Substituindo na equação (I) obtemos a tensão na corda:
Mm
T= g
M +m 119

120. Exemplo 5-5
• Na Figura, uma corda puxa para cima uma
caixa de biscoitos ao longo de um plano
inclinado sem atrito cujo ângulo é θ = 30o
A massa da caixa é m=5kg, e o módulo da força
exercida pela corda é T=25N. Qual é a
componente a da aceleração da caixa ao
longo do plano inclinado?
120

121. Corda
θ
121

122. Solução
• Diagrama de corpo livre para o bloco:

FN

T
y

x 90º-θ Fg
122

123. O movimento se dá ao longo do eixo x (paralelo ao plano inclinado) a componente da
força gravitacional é negativa e tem módulo dado pelo produto do peso pelo seno da
inclinação do plano inclinado. Portanto a segunda lei de Newton para este caso é:
T − mgsenθ = ma T
a= − gsenθ
m
Se a tensão da corda estivesse ausente, a inclinação do plano iria reduzir a
aceleração do bloco (comparando com uma queda livre) com um fator dado pelo
seno da inclinação do plano inclinado. O valor da aceleração é dado por:
m
a = 0,1 2
s
Portanto o bloco acelera para cima com uma aceleração de módulo baixo. Na
ausência da corda cairia com uma aceleração menor em módulo que a aceleração
da gravidade.
123

124. Exemplo 5-7
• A Figura mostra um arranjo no qual duas forças são

aplicadas a um bloco de 4kg em um piso sem atrito,
F1
mas apenas a força está indicada. Essa força tem
módulo fixo, mas o ângulo θ entre ela e o semi-eixo x

positivo pode variar. A força é horizontal e seu
F2
módulo é constante. A Figura mostra a aceleração
horizontal ax do bloco em função de θ no intervalo
. Qual é o valor de ax para θ=180º ?
0 ≤ θ ≤ 90
o
124

125.  ax (m/s2)
F1 3
θ
2
1
0o 90o
θ
125

126. Solução
• A segunda lei de Newton para o bloco pode ser aplicada
apenas para a direção onde ocorre o movimento (eixo x):
F1 cos θ + F2 = ma
• Podemos usar o primeiro ponto do gráfico para obter:
F1 + F2 = 12 N (I )
• O segundo ponto do gráfico fornece uma segunda equação:
F2 = 2 N ( II )
• Substituindo a segunda equação na primeira equação,
obtemos:
F1 = 10 N
126

127. Portanto a aceleração para um ângulo de 180º será:
F1 F2
a x = cos180 +
0
m m
A aceleração para esse ângulo vale:
m
a x = −2 2
s
127

128. Exemplo 5-9
128

129. A
B
129

130. Solução
• Diagrama de corpo livre para o bloco A:
130

131. • Diagrama de corpo livre para o bloco B:
131

132. 132

133. 133

134. Exemplo 6-5
134

135. Solução
135

136. 136

137. Atrito
• Atrito é a resistência que uma superfície impõe a um corpo se movendo sobre
ela.
• O atrito é tangencial à superfície envolvida.
• O atrito é uma força oposta a força (resultante) que atua sobre um corpo, fazendo
com que ele se mova (ou tenha tendência a se mover) sobre uma superfície.
• O atrito passa por três etapas. Primeiro, o atrito equilibra a força resultante que
age sobre corpo sobre a superfície. Segundo, o atrito atinge um valor máximo, na
iminência do movimento, de módulo proporcional à força normal que age sobre o
corpo. Terceiro, quando o corpo se move o atrito reduz seu valor, mas ainda é
proporcional à força normal que a superfície impõe sobre o corpo.
• Juntos, atrito e força normal, representam as forças que uma superfície realiza
sobre um corpo em contato com ela. A força normal empurra o corpo para fora da
superfície e o atrito impede o movimento do corpo sobre a superfície.
137

138. Propriedades do Atrito
138

139. Exemplo 6-1
Se a roda de um carro estiver travada (impedida de
girar) durante uma frenagem de emergência, o carro
desliza pela pista. Pedaços queimados de pneus e
pequenos trechos derretidos da pista formam as
marcas de derrapagem. O recorde de marcas de
derrapagem que ocorreu em uma via pública
aconteceu em 1960 em um Jaguar na rodovia M1 na
Inglaterra – as marcas tinha 290m de comprimento!
139

140. v=0
290m
140

141. Solução
• Diagrama de corpo livre para o carro:
141

142. 142

143. Exemplo 6-3
143

144. O bloco desliza sobre uma rampa e está preso por várias cordas
(apenas uma é mostrada). A rampa é lubrificada com água para
diminuir o coeficiente de atrito estático para 0,4. Assuma atrito
desprezível no ponto (lubrificado) onde as cordas passam pelo
canto superior da rampa. Se cada homem homem no topo da
pirâmide puxa com uma força (razoável) de 686 N , quantos
homens são necessários para colocar o bloco na iminência do
movimento?
x
y θ
144

145. Solução
• Diagrama de corpo livre para o bloco:
θ
145

146. 146

147. Força Centrípeta
147

148. Exemplo 6-7
• Em um apresentação circense de 1901, Allo
“Dare Devil” Diavolo apresentou o desafio de
fazer uma bicicleta atravessar um loop
(Figura). Assumindo que o loop é um círculo
de raio R=2,7m, qual é a menor velocidade
que Diavolo deve ter no topo do loop para
permanecer em contato com a pista?
148

149. R
149

150. Solução
• Diagrama de corpo livre no topo do loop:
Direção centrípeta
150

151. 151

152. Exemplo 6-8
• Até mesmo os aficionados por montanha-
russa se amedrontam quando pensam no
Rotor, que é essencialmente um grande
cilindro oco que está rodando em torno do
seu eixo central. Antes de uma volta começar,
o participante entra por uma porta lateral e se
apoia em uma parede coberta com uma lona.
A porta é fechada e quando o cilindro começa
a girar, o participante e a parede giram juntos.
152

153. 153

154. Solução
• Diagrama de corpo livre para o participante
y 
 fs
FN
Direção centrípeta 
Fg
154

155. (a) A segunda lei de Newton possui duas componentes: a centrípeta e a vertical
 f s − Fg = 0

 v2
 FN = m R

A força de atrito estática é sempre menor que o produto do coeficiente de atrito
estático pelo módulo da força normal:
R R f s Rg Rg
v = FN ≥
2
= , v≥
m m µs µs µs
Portanto a velocidade mínima será dada por:
Rg 2,1m9,8m / s 2
vmin = = = 7,17m / s
µs 0,4
155

156. (b) O módulo da força centrípeta é dado pela componente centrípeta da segunda lei de
Newton:
v2
FN = m = 49kg
( 7,17m / s ) = 1.200 N2
R 2,1m
156

157. Energia Cinética e Trabalho
Unidade IV
157

158. 6.4 Energia Cinética
158

159. Exemplo 7-1
• Em 1896 em Waco, Texas, William Crush estacionou
duas locomotivas em lados opostos de um ferrovia
de 6,4km de comprimento, e as permitiu colidir na
velocidade máxima na frente de 30.000
espectadores. Assumindo que cada locomotiva
pesava 1,2x106N e que a aceleração foi constante e
igual à 0,26 m/s2, qual era a energia cinética total das
duas locomotivas imediatamente antes da colisão?
159

160. Solução
• Podemos usar a Equação de Toriccelli para
obter a velocidade das duas locomotivas no
instante da colisão:
v 2 = v0 + 2a∆x = 0 2 + 2 ⋅ 0,26m / s 2 ⋅ 3,2 ×103 m, v = 40,8m / s
2
• A massa de cada locomotiva é dada por:
P 1,2 ⋅106 N
m= = = 1,22 × 105 kg
g 9,8m / s 2
• A energia cinética total das duas locomotivas
é dada por: = 2 1 mv  = 1,22 ×10 kg ( 40,8m / s ) = 2 ×10 J
K 
2

2 5 2 8
 
160

161. Trabalho de uma força constante e de
uma força variável
W = Fd cos θ W = Fx ⋅ ∆x + Fy ⋅ ∆y
161

162. Trabalho (conceito)
• O trabalho é a quantidade de energia
necessária para fazer a partícula romper com
seu estado de equilíbrio.
• Somente as componentes da força paralelas
ao deslocamento contribuem para o trabalho.
• Energia é a capacidade de um sistema físico
de mudar ao longo do tempo.
162

163. 163

164. Exemplo 7-2
• Dois espiões industriais estão deslizando um cofre de massa 225kg,
inicialmente estacionário, de um deslocamento de módulo 8,5m ao longo
da horizontal, indo na direção do caminhão deles. O empurrão do espião
001 faz um ângulo de 30o com a horizontal e aponta para baixo e tem
módulo 12N; o empurrão do espião 002 tem módulo 10N e faz um ângulo
de 40o com a horizontal e aponta para cima. O módulo e a direção das
forças não mudam quando o cofre é deslocado horizontalmente, e o
atrito entre o cofre e o piso é desprezível.
• (a) Qual o trabalho total feito pelos dois espiões durante o deslocamento
do cofre?
• (b) Durante o deslocamento, qual é o trabalho da força gravitacional
sobre o cofre e qual o trabalho da força normal do piso sobre o cofre?
• (c) O cofre está inicialmente em repouso, qual é a velocidade final do
cofre após do deslocamento?
164

165. Solução
• (a) O trabalho realizado pelo espião 001 é
dado por:
 
W1 = F1 • d = F1d cos θ = 12 N 8,5m cos 300 = 88,33 J
• O trabalho realizado pelo espião 002 é dado
 
por: W = F • d = 10 N 8,5m cos 40 = 65,11J
2 2
o
• O trabalho total é a soma do trabalho dos dois
espiões:
W = W1 + W2 = 153,4 J
165

166. (b) O trabalho da força gravitacional é dado por:
Wg = Fg d cos 900 = 0
O trabalho da força normal é dado por:
(
W = FN d cos − 90 0 = 0 )
Ambos trabalhos são nulos, pois as forças gravitacional e normal são perpendiculares
ao deslocamento!
(c) O trabalho total é portanto dado pela soma do trabalho dos dois espiões e é igual a
variação da energia cinética (teorema do trabalho e energia cinética):
1 2 1 2 2W
W = ∆K = mv f − m0 , v 2 =
f
2 2 m
A velocidade final é dada por: 2W 2(153,4 J )
vf = = = 1,17m / s
m 225kg
166

167. Trabalho realizado pela força
gravitacional
• Como a força gravitacional aponta na direção
vertical e é constante, temos:
W = m⋅ g ⋅( y
g inicial−y )
final
• A massa da partícula é m, o módulo da
aceleração da gravidade é g e y é a altura do
objeto.
167

168. Exemplo 7-6
• Um elevador de massa m=500kg está descendo com
vi = 4m / s
velocidade ,quando o cabo de sustentação começa a

 g
deslizar fazendo com que o elevador caia com aceleração
a=
5
• (a) Durante a queda de 12m, qual é o trabalho da força
gravitacional sobre o elevador?
• (b) Durante a queda de 12m, qual é o trabalho sobre o
elevador realizado pela tensão no cabo de sustentação?
• (c) Qual é o trabalho resultante sobre o elevador durante a
queda?
• (d)Qual é a energia cinética do elevador no fim da queda de
12m?
168

169. Solução
• (a) O trabalho da força gravitacional é dado
por:W = − m ⋅ g ⋅ ∆ y = − 500kg ⋅ 9,8m / s ⋅ ( − 12m) = 5,88 × 10 J
g
2 4
• (b) Para obter o trabalho da tensão no cabo,
considere a segunda lei de Newton:
 g 4
T − Fg = m ⋅ a, T − mg = m − , T = m ⋅ g
 5 5
• O trabalho da tensão na corda será dado por:
4 4
WT = Td cos 180 0 = − mgd = − 500kg ⋅ 9,8m / s 2 ⋅12m = −4,7 × 10 4 J
5 5
169

170. (c) O trabalho total é a soma dos trabalhos da força gravitacional e da tensão no cabo:
W = WT + Wg = 1,18 ×10 4 J
(d) A energia cinética final pode ser obtida através do teorema do trabalho e energia
cinética, utilizando o trabalho total e a velocidade inicial:
W = ∆K = K f − K i
1 2 1
mvi + W = 500kg ( 4m / s ) + 1,18 ×10 4 J = 1,58 × 10 4 J
2
Kf =
2 2
170

171. Trabalho da força elástica
• A força elástica é diretamente oposta ao
sentido do deslocamento da mola, portanto é
uma força variável. Seu trabalho é dado por:
1 2 1 2
We = ⋅ k ⋅ xinicial − ⋅ k ⋅ x final
2 2
• A constante de mola é k e x é o deslocamento
da mola.
171

172. Exemplo 7-8
• Na Figura, um pote de cominho de massa
m=0,4kg desliza sobre uma superfície
horizontal sem atrito com uma velocidade
v=0,5m/s. Então atinge uma mola de
constante elástica k=750N/m e a comprime.
Quando o pote é parado momentaneamente
pela mola, de que distância d a mola é
comprimida?
172

173. k 
v
m
Sem atrito
173

174. Solução
• O trabalho da força elástica é dado por:
1 2 1 2 1 2 1 1
kxi − kx f = k 0 − k ( − d ) = − kd 2
2
W=
2 2 2 2 2
• A variação da energia cinética é dada por:
1 2 1 2 1 2 1 2 1
∆K = mv f − mvi = m0 − mv = − mv 2
2 2 2 2 2
• O teorema do trabalho e energia cinética diz
que: 1 1 m 0,4kg
kd 2 = mv 2 , d = v= 0,5m / s = 1,2 ×10 − 2 m = 1,2cm
2 2 k 750 N / m
174

175. Potência
• A potência média de uma força, atuando durante um
intervalo de tempo Δt, é dada pelo razão do trabalho
realizado pela força pelo intervalo de tempo:
W
Pmédia =
∆t
• A potência instantânea é dada pela derivada do trabalho
realizado pela força em relação ao tempo:
dW
P =
dt
• A unidade de potência no S.I. é o Watt (W).
175

176. Podemos relacionar a potência média com a força média atuando sobre a partícula e a
velocidade média:
 
Pmédia = Fmédia • vmédia = Fmédia vmédia
Também podemos relacionar a potência instantânea diretamente com a força aplicada
sobre a partícula, e a sua velocidade instantânea:
 
P = F • v = Fv cos θ
Durante o movimento de uma máquina mecânica (por exemplo, um carro), somente a
energia dissipada para o ambiente não é utilizada pela máquina. Podemos definir o
rendimento da máquina, η, como a razão entre a potência utilizada, Pu , e a potência
total fornecida à máquina, que é soma da potência utilizada com a potência dissipada,
Pt = Pu + Pd . Sendo assim,
Pu
η=
Pt
176

177. Exemplo 7-11
• Duas forças constantes agindo sobre uma caixa
quando a caixa se desloca para a direita sobre um
piso sem atrito. A primeira força é horizontal e
aponta no sentido oposto ao da velocidade, com
módulo 12N; a segunda força faz um ângulo de 60o
com o piso e tem módulo 4N. A velocidade da caixa
em certo instante é 3 m/s. Qual é a potência devida à
cada força naquele instante e qual a potência
resultante? O trabalho total está variando naquele
instante?
177

178. Solução
• A potência da primeira força é dada por:
 
P = F1 • v = F1v cos 180 o = 2 N ⋅ 3m / s ⋅ −1 = −6W
1
• A potência da segunda força é dada por:
 
P2 = F2 • v = F2 v cos 600 = 4 N ⋅ 3m / s ⋅ 0,5 = 6W
• A potência resultante é dada pela soma das duas
potências: P=0
• Como a potência é a derivada do trabalho em
relação ao tempo, temos que o trabalho não está
variando naquele instante.
178

179. Energia Potencial e Conservação
de Energia
Unidade IV
179

180. Energia Potencial
180

181. •O valor numérico da energia potencial depende de um
valor de referência escolhido pelo observador. Geralmente
o valor da energia potencial na origem (onde está o
observador), ou no infinito (muito distante do observador).
•Este valor de referência é, geralmente, o número zero.
•A energia potencial, assim, se torna uma função da posição
atribuindo valores em energia para a possibilidade da
partícula passar por a posição observada.
•O trabalho é realizado através da extração da energia
potencial do sistema; transformando potencial em energia
cinética, fazendo a partícula sair de uma posição para outra.
181

182. A força aplicada sobre a partícula pode ser obtida a partir da energia potencial:
dU
F =−
dx
Um mínimo na energia potencial corresponde a um ponto de equilíbrio estável
(onde a força sobre a partícula é nula, sem causas para se mover naquele ponto).
U
Um máximo na energia potencial corresponde a um ponto de equilíbrio instável
x
(onde a força sobre a partícula é nula, sem causas para se mover naquele ponto).
U
x
182

183. Exemplo 8-2
• Uma preguiça repousa sobre um galho colocado a 5m acima
do solo.
• (a) Qual é a energia potencial gravitacional U do sistema
Terra-preguiça se o ponto de referência y=0 é escolhido como
sendo (1) o solo, (2) um balcão três metros acima do solo, (3)
no galho, (4) 1 m acima do galho? Considere a energia
potencial gravitacional como sendo nula em y=0.
• (b) A preguiça desce até o chão. Em cada situação qual á a
variação da energia potencial gravitacional do sistema Terra-
preguiça durante a descida?
183

184. Solução
• (a) (1) Tomando o solo como ponto de
referência, temos para a energia potencial
gravitacional: U = mgy = 2kg ⋅ 9,8m / s 2 ⋅ 5m = 98 J
• (2) Considerando o balcão como ponto de
referência, a altura da preguiça vale 2m,
portanto: U = mgy = 2kg ⋅ 9,8m / s 2 ⋅ 2m = 39,2 J
• (3) Tomando o galho como ponto de
referência, a altura da preguiça vale 0,
portanto: U = mgy = 2kg ⋅ 9,8m / s ⋅ 0 = 0 J
2
184

185. (4) Escolhendo o ponto de referência como estando a um 1m acima do galho, a altura da
preguiça vale -1m, portanto:
U = mgy = 2kg ⋅ 9,8m / s 2 ⋅ ( − 1m ) = −19,6 J
(b) Para todos os pontos de referência observa-se que a variação na altura da preguiça foi
-5m, portanto a variação na energia potencial será a mesma nas quatro situações:
∆U = mg∆y = 2kg ⋅ 9,8m / s 2 ⋅ ( − 5m ) = −98 J
185

186. Força conservativa e força dissipativa
• Força conservativa é aquela em que o
trabalho em uma trajetória fechada é nulo.
Com isso o trabalho da força conservativa
independe do caminho. Exemplo: força
gravitacional e força elástica.
• Força dissipativa é aquela em que o trabalho
em uma trajetória fechada é diferente de
zero. Exemplo: força de atrito.
186

187. Energia Mecânica
• A energia mecânica é a soma da energia cinética com
a energia potencial:
Emecânica = K + U
• Para partículas submetidas à uma força conservativa,
temos um dos princípios mais queridos da Física: a
conservação da energia (mecânica)! A energia
mecânica não muda com o passar do tempo.
Einicial = E final
187

188. •No caso de forças dissipativas, a energia mecânica não é
conservada. Neste caso, ela se transforma em outras formas de
energia: calor, som, etc. Sendo assim, a energia mecânica
acaba diminuindo, enquanto a energia do ambiente (onde a
partícula se encontra) acaba aumentando; através da injeção
de energia devida ao trabalho das forças dissipativas.
• O trabalho das forças dissipativas é igual a variação da energia
mecânica do sistema:
Wdissipativas = ∆Emecânica
•Apesar da energia mecânica não ser conservada, a energia do
sistema : ambiente mais partícula é conservada. Sendo assim,
podemos garantir que a energia (total) ainda é conservada.
188

189. Exemplo 8-3
• Uma criança de massa m desce até o solo
através de um toboágua à uma altura de 8,5m
acima do solo. Assumindo que o toboágua é
uma superfície sem atrito devido à água
contida nele, obtenha a velocidade da criança
quando ela chega ao solo.
189

190. Solução
• Como não existe atrito no toboágua, a energia
mecânica é conservada durante o
deslocamento da criança. No alto do toboágua
a sua energia mecânica é devida à energia
potencial:
Etopo = mgh
• Quando chega no solo, a energia mecânica da
criança é devida somente a energia cinética:
1 2
Esolo = mv
2
190

191. Como a energia mecânica se conserva, temos a seguinte equação:
Etopo = Esolo
1 2
mgh = mv
2
v = 2 gh = 2 ⋅ 9,8m / s 2 ⋅ 8,5m = 13m / s
191

192. Exemplo 8-7
• Na Figura, um pacote de pamonha desliza sobre um
piso com velocidade . Ele atinge, então, uma
i v = 4m / s
mola; comprimindo-a até parar momentaneamente.
O caminho até a mola, inicialmente relaxada, é sem
atrito, mas a partir do instante em que o pacote
começa a comprimir a mola, uma força de atrito de
módulo 15N atua sobre o pacote. Se k=10.000 N/m,
de que distância d a mola é comprimida pelo pacote?
192

193. 
vi
k
Pacote de Pamonha
193

194. Solução
• Como existe atrito durante a compressão da mola,
não podemos assumir que a energia mecânica se
conserva. Neste caso o trabalho da força de atrito
será igual a variação na energia mecânica. A energia
mecânica inicial era devida à energia cinética do
pacote: 1 2
Ei = mvi
2
• A energia mecânica final é devida à energia potencial
elástica da mola: 1
k(− d )
2
Ef =
2
194

195. O trabalho da força de atrito será dado por:
W = fk ⋅ ( − d ) = − fk ⋅ d
Este trabalho será igual a variação na energia mecânica:
W = ∆E = E f − Ei
A equação anterior pode ser escrita na seguinte forma:
1 2 1
kd + f k d − mvi2 = 0
2 2
Cuja solução será:
− fk + f k2 + kmvi2
d=
k
A solução negativa foi esquecida pois seria uma solução inválida, pois apontaria uma
distensão da mola e não uma compressão. Substituindo os valores:
− 15 N + (15 N ) 2 + (10.000 N / m) ⋅ 2kg ⋅ ( 4m / s )
2
d= = 0,055m = 5,5cm
10.000 N / m
195

196. Exemplo 8-8
• A figura mostra uma encosta montanhosa e
um vale aonde um deslizamento acontece. As
rochas tem uma massa total m, caem de uma
altura y=H, movem-se de uma distância d1 ao
longo de uma encosta de inclinação θ=450 , e
depois movem de uma distância d2 ao longo
d
de um vale plano. Qual é a razão , se o
2
H
coeficiente de atrito cinético tem um valor
razoável de 0,6?
196

197. Rochas
y=H
d1
θ d2
y=0
Vale
197

198. Solução
• A energia mecânica no início deslizamento é
devida apenas a energia potencial
gravitacional das rochas:
Ei = mgH
• A energia mecânica final é nula:
Ef = 0
• Para obter a força de atrito na encosta
considere o diagrama de corpo livre:
198

199. y

FN

x fk

Fg θ
θ
A segunda Lei de Newton para a componente y é dada por:
FN − mg cos θ = 0
De maneira que a força de atrito cinética será dada por:
f k ,1 = µ k mg cos θ
199

200. Para obter a força de atrito cinético no vale, vamos utilizar o seguinte diagrama de corpo
livre:

FN
y
x 
fk

Fg
A segunda Lei de Newton para a componente y é dada por:
FN − mg = 0
Portanto a força de atrito cinético no vale será:
f k , 2 = µ k mg
O trabalho da força de atrito será dado por:
W = ( − f k ,1 ) d1 + ( − f k , 2 ) d 2 = − µ k mgd1 cos θ − µ k mgd 2
200

201. A distância d1 pode ser obtida em termos da altura da encosta, H, através do uso da
trigonometria:
H H
senθ = , d1 =
d1 senθ
De maneira que o trabalho da força de atrito é dado por:
 H 
W = − µ k mg  + d2 
 tan θ 
O trabalho da força de atrito é igual a variação na energia mecânica:
 H 
W = ∆E , − µ k mg  + d 2  = −mgH
 tan θ 
Resolvendo a equação anterior para d2/H, nós obtemos:
d2 1 1 1 1
= − = − = 0,67
H µ k tan θ 0,6 tan 45 0
201

202. Centro de Massa e Momento
Linear
Unidade V
202

203. Centro de Massa
• O centro de massa é a partícula equivalente que
substitui todas as partículas de um sistema,
possuindo a massa total do sistema de partículas.
• O centro de massa é a média ponderada das
posições das partículas, com a massa de cada
partícula sendo o peso associado à cada posição da
partícula:
n n n
∑m x i i ∑m y i i ∑m z i i
xCM = i =1
n
, yCM = i =1
n
, zCM = i =1
n
∑m
i =1
i ∑m
i =1
i ∑m
i =1
i
203

204. Exemplo 9-1
• Três partículas de massa m1=1,2kg, m2=2,5kg e
m3=3,4kg formam um triângulo equilátero de
lado a=140 cm. Qual é o centro de massa do
sistema? m
3
y
a
a
m1
m2
a
x
204

205. Solução
• As posições das partículas são dadas por:
Partícula Componente x da Componente y da
posição posição
1 0 0
2 a=140cm 0
3 a/2=70cm 3
a = 120cm
2
• Componente x do centro de massa:
m1 x1 + m2 x2 + m3 x3 1,2kg ⋅ 0 + 2,5kg ⋅140cm + 3,4kg ⋅ 70cm
xCM = = = 83cm
m1 + m2 + m3 1,2kg + 2,5kg + 3,4kg
205

206. Componente y do centro de massa:
m1 y1 + m2 y2 + m3 y 3 1,2kg ⋅ 0 + 2,5kg ⋅ 0 + 3,4kg ⋅120cm
yCM = = = 58cm
m1 + m2 + m3 1,2kg + 2,5kg + 3,4kg
206

207. Para o caso de um corpo contínuo, devemos trocar a soma por um integral e as
massas pela densidade (“derivada” da massa em relação ao comprimento, área e
volume do corpo).
Unidimensional:
xCM =
∫ xλdl , yCM =
∫ yλdl , zCM =
∫ zλdl
M M M
Bidimensional:
xCM =
∫ xσdA , yCM =
∫ yσdA , zCM =
∫ zσdA
M M M
Tridimensional:
xCM =
∫ xρdV , yCM =
∫ yρdV , zCM =
∫ zρdV
M M M
207

208. Exemplo 9-2
• A Figura mostra um disco de densidade
superficial de massa uniforme de raio 2R em
que um buraco de raio R foi feito em uma
linha de montagem. Utilizando o sistema de
coordenadas xy mostrado, encontre a posição
do centro de massa do disco.
208

209. y
x
209

210. Solução
• Primeiro devemos encontrar o centro de
massa de um disco homogêneo. Como a
densidade superficial de massa é constante,
apenas devemos buscar o centróide (centro
geométrico) do disco:
R 2π R 2π
∫ ∫ r cosθrdθdr ∫ ∫ rsenθrdθdr
xCM = 0 0
= 0, yCM = 0 0
=0
πR 2
πR 2
• Portanto o centróide se localiza no centro do
disco!
210

211. O centro de massa da placa poderá ser obtido através do centro de massa do disco
completo, para isso considere o disco sendo composta pelo disco com o buraco, S, e o
buraco, B, D=S+B. Sendo o disco composto por essas duas partículas, nós obtemos a
seguinte equação:
xD =
( 2
)
π ( 2 R ) − R 2 xS + πR 2 ⋅ (− R)
=0
π ( 2R)
2
yD =
( 2
)
π ( 2 R ) − R 2 y S + πR 2 ⋅ (0)
=0
π ( 2R )
2
Resolvendo as duas equações, nós encontramos a posição do disco com o buraco:
 R
 xs =
 3
 ys = 0

211

212. A força que atua sobre a partícula equivalente, o centro de massa é a força
resultante que atua no sistema de partículas (ou corpo contínuo). A massa do centro
de massa é a massa total do sistema de partículas, M; sua aceleração é a derivada
segunda da posição do centro de massa em relação ao tempo.
A segunda lei de Newton para o centro de massa é dada por:
Fres , x = M ⋅ aCM , x , Fres , y = M ⋅ aCM , y , Fres , z = M ⋅ aCM , z ,
onde
n
M = ∑ mi ,
i =1
d 2 xCM d 2 yCM d 2 zCM
aCM , x = , aCM , y = , aCM , z =
dt 2 dt 2 dt 2
212

213. Exemplo 9-3
• As três partículas na Figura estão inicialmente
em repouso. Cada uma experimenta forças
devidas às partículas fora do sistema. As
direções estão indicadas, e os módulos são F1
= 6N, F2=12N e F3=14N. Qual a aceleração do
centro de massa do sistema, e em que direção
ele se move?
213

214. y
θ=45o
4kg 8kg
x
4kg
214

215. Solução
215

216. 216

217. Momento linear
• O momento é relacionado com a capacidade
de um ente físico mudar de um lugar para
outro (no espaço).
• Para uma partícula pontual (ponto dotado de
massa), o momento linear (em um sistema
coordenadas cartesiano, referencial de
Galileu) é dado por:
 
p = m⋅v
217

218. Momento linear do C.M.
• Para um sistema de partículas, o momento do sistema de
partículas é o momento do centro de massa (momento da
partícula equivalente)
• O momento do centro de massa é a soma dos momentos de
cada partícula:
 n  
 drCM
PCM = ∑ mi ⋅ vi , PCM = M ⋅
i =1 dt
• Para o caso contínuo, o momento do centro de massa
(momento do corpo) é dado em termos da densidade de
massa:  
P = ∫ ρv dV
218

219. Impulso
• O impulso, J, de uma força mede o quanto a
força (efetivamente) contribuiu para produzir
movimento sobre a partícula em um intervalo
de tempo:
  
J = ∫ F ⋅ dt = Fmédia ⋅ ∆t
• Através da segunda lei de Newton, podemos
obter o teorema do impulso momento-linear:
      
J res = ∆p = p f − pi , J res = PCM , f − PCM ,i
219

220. Exemplo 9-5
• Colisão contra o muro de carros de corrida. A Figura é uma
vista superior da trajetória de um carro de corrida quando
entra em rota de colisão com um muro de proteção.
Imediatamente antes da colisão, ele está trafegando com
uma velocidade vi=70m/s ao longo de uma linha reta fazendo
um ângulo de 30º com o muro. Imediatamente depois da
colisão a velocidade era vf=50m/s e fazia um ângulo de 10º
com o muro. A massa do piloto é m=80kg.
• (a) Qual é o impulso sobre o piloto devido à colisão?
• (b) A colisão dura 14ms. Qual é o módulo da força média que
age sobre o piloto durante a colisão?
220

221. Solução
221

222. 222

223. O impulso faz com que a conservação do momento seja quebrada. Sendo assim, somente
a presença da força durante aquele intervalo de tempo impede a conservação do
momento.
Choques Mecânicos
Tipo de Choque Conservação Condição do sistema
de partículas
Elástico. Energia Cinética. Isolado.
Momento Linear. Sem forças internas.
Inelástico. Momento Linear. Isolado.
Com forças internas.
223

224. Conservação do momento linear
• Se as forças externas que atuam sobre um
sistema possuem uma resultante nula, o
momento linear é conservado.
 
Pinicial = Pfinal
• Isto se deve à forma geral da segunda lei de
Newton (que admite a mudança da massa
com o decorrer do tempo):
 
 dp  dP
Fres = , Fres = CM
dt dt
224

225. Exemplo 9-6
• Explosão unidimensional. Uma urna de
votação de massa m=6kg desliza com
velocidade v=4 m/s em um piso sem atrito no
sentido positivo de um eixo x. A urna explode
em dois pedaços. Um pedaço, de massa
m1=2kg, se move no sentido positivo do eixo x
com velocidade v1=8 m/s. Qual é a velocidade
do segundo pedaço, de massa m2?
225

226. Solução
226

227. 227

228. Exemplo 9-8
228

229. y
A C
80o
B
x
50o
229

230. Solução
230

231. 231

232. Exemplo 9-9
• O pêndulo balístico era usado para medir a velocidade de
projéteis antes que os dispositivos eletrônicos fossem
inventados. A versão mostrada na Figura era composta por
um grande bloco de madeira de massa M=5,4kg, pendurado
por duas cordas compridas. Uma bala de massa m=9,5g é
disparada contra o bloco e sua velocidade se anula
rapidamente. O sistema bloco-bala oscila para cima, com o
centro de massa subindo a uma distância h=6,3 cm antes de o
pêndulo parar momentaneamente no final da trajetória em
arco de circunferência. Qual é a velocidade da bala antes da
colisão?
232

233. M
m
h
233

234. Solução
• Como a velocidade da bala se anula
rapidamente, forças internas agem dentro do
sistema. Entretanto, as forças externas
durante o impacto são nulas (a força
gravitacional e a tensão na corda se anulam).
Dessa forma, o momento linear é conservado
e a energia cinética não é conservada, ou seja,
a colisão é inelástica.
234

235. 235

236. 236

237. Exemplo 9-11
• Duas esferas metálicas, inicialmente
suspensas por cordas verticais, apenas se
tocam, como mostra a Figura. A esfera 1, de
massa m1=30g, é puxada para a esquerda até a
altura h1=8cm e liberada a partir do repouso.
Na parte mais baixa da trajetória ela sofre
uma colisão elástica com a esfera 2, cuja
massa é m2=75g. Qual é a velocidade v1f da
esfera 1 imediatamente após a colisão?
237

238. h1
1
2
m1
m2
238

239. Solução
239

240. 240

241. 241

242. Rotação
Unidade VI
242

243. Cinemática da rotação
• Uma rotação é um movimento que efetua
arcos de círculo em torno de um eixo (fixo) no
espaço. Para estudar uma rotação devemos
utilizar as coordenadas cilíndricas (raio, ângulo
e coordenada cartesiana ao longo do eixo). Se
durante a trajetória, a partícula mantém seu
raio fixo e o plano de rotação também,
podemos determinar a posição da partícula
através de um ângulo (unidade do S.I. é
radiano).
243

244. y
r
θ
Eixo de rotação
x
Coordenadas cartesianas: (x,y,z)
z Coordenadas cilíndricas: (r,θ,z)
244

245. Deslocamento angular
• Quando a partícula muda de um ângulo para
outro, ela deixa um pequeno rastro em forma
de arco de círculo; o deslocamento angular:
∆θ = θ 2 − θ1
Unidade do S.I.: radiano (rad)
245

246. Velocidade Angular
• A velocidade angular média é a razão entre o
deslocamento angular realizado e o intervalo
de tempo gasta para efetuá-lo:
∆θ
ω=
∆t
• A velocidade angular instantânea é a derivada
do ângulo em relação ao tempo:
dθ
ω=
dt
246

247. Aceleração Angular
247

248. Exemplo 10-1
248

249. Solução
• (a) Para fazer o gráfico considere a seguinte
tabela para a posição angular
t(segundos) Θ(radianos)
-3 3,05
0 -1
5,4 3,05
249

250. 250

251. Considere a seguinte tabela para a dependência da velocidade angular em relação ao
tempo
t(segundos) ω(radianos/segundo)
-3 -2,1
6 2,4
251

252. (d) O movimento se inicia no segundo quadrante
com sentido do movimento dado pelo sentido
horário. Segue indo para o quarto quadrante e a
partir de 1,2 segundos o sentido do movimento
muda para o sentido anti-horário atingindo o
primeiro quadrante em 2,8 segundos e depois
retornando para o segundo quadrante
completando uma volta.
252

253. Movimento Circular Uniformemente
Variado (M.C.U.V.)
253

254. Exemplo 10-3
254

255. Solução
255

256. 256

257. Decomposição em coordenadas
polares
257

258. 258

259. 259

260. Exemplo 10-5
260

261. (a) Que ângulo θP o arco deve subtender para que a seja 4g no ponto P?
(b) Qual é o módulo a da aceleração experimentada pelo passageiro no ponto P e depois
de passar pelo ponto P?
P
θP
Ponto de embarque
261

262. Solução
262

263. 263

264. Momento de Inércia
• Assim como modificamos a causa para uma rotação, devemos
modificar a inércia para a rotação.
• A inércia da rotação é dada pela distribuição das massas em
torno do eixo de rotação (momento de segunda ordem):
• Partícula pontual:
I = m⋅r2
• Sistema de partículas:
n
I = ∑ mi ⋅ ri 2
i =1
• Corpo contínuo:
I = ∫ r 2 λdl , I = ∫ r 2σdA, I = ∫ r 2 ρdV
264

265. Teorema dos Eixos Paralelos
265

266. Exemplo 10-6
• A Figura mostra um corpo rígido formado por duas
partículas de massa m ligadas por uma barra de
comprimento L e massa desprezível.
• (a) Qual é o momento de inércia ICM em relação a um
eixo passando pelo centro de massa e perpendicular
à barra?
• (b) Qual é o momento de inércia I do corpo em
relação a um eixo passando pela extremidade
esquerda da barra e paralelo ao primeiro eixo?
266

267. m m
CM
L/2
L/2
267

268. Solução
268

269. Exemplo 10-7
• Considere uma barra fina, uniforme, de massa M e
comprimento L, sobre um eixo x cuja origem está no
centro da barra.
• (a) Qual é o momento de inércia em relação a um
eixo perpendicular à barra passando pelo seu
centro?
• (b) Qual é o momento de inércia I da barra em
relação a um novo eixo perpendicular à barra
passando pela extremidade esquerda?
269

270. Solução
270

271. 271

272. Energia Cinética da Rotação
• Uma partícula, sistema de partículas ou corpo
contínuo girando em torno de um eixo fixo no
espaço possui energia cinética dada por:
1 2
K = Iω
2
• I é o momento de inércia e ω é a velocidade
angular.
272

273. Torque
• Diante de uma rotação, temos que modificar a causa do
movimento de uma força (linear, cartesiana) para o torque :
  
τ = r×F
• O torque, definido pelo produto vetorial, aponta na direção
do eixo de rotação.
• Somente forças perpendiculares à direção radial são capazes
de modificar uma rotação.
• As coordenadas cilíndricas (r,θ e z), possuem uma coordenada
reta. Em razão disso, o torque (causa de uma rotação) é um
vetor; como a causa de uma translação (força).
273

274. Eixo de rotação. ˆ
i ˆ
j ˆ
k

τ = x y z

τ Fx Fy Fz

r

F
τ = r ⋅ F ⋅ sen(θ ) = r⊥ ⋅ F = r ⋅ F⊥
θ é o ângulo entre o vetor posição e a força.
r⊥
é o braço de alavanca.
F⊥
é a componente tangencial da força.
274

275. Segunda Lei de Newton para Rotações
• Com as modificações na inércia e na massa,
podemos obter a segunda lei de Newton para
rotações:
τ = I ⋅α
• Como se vê basta modificar a causa (torque),
efeito (aceleração angular) e inércia
(momento de inércia).
275

276. Exemplo 11-3
276

277. z
θ y
x
277

278. Solução
278

279. O torque associado à terceira força é dado por:
ˆ
i ˆ
j kˆ

τ 3 = 2,6m 0 1,5m = ( 3 N ⋅ m ) i + ( − 5,2 N ⋅ m ) k
ˆ ˆ
0 − 2N 0
279

280. Exemplo 10-9
• A Figura mostra um disco uniforme com
massa M=2,5kg e raio R=20cm, montado em
uma eixo fixo horizontal. Um bloco de massa
m=1,2kg está pendurado em uma corda sem
massa que está enrolada na circunferência do
disco. Encontre a aceleração do bloco que cai,
a aceleração angular do disco e a tensão na
corda. A corda não desliza e não há atrito no
eixo de rotação.
280

281. M
m
281

282. Solução
• Diagrama de corpo livre para o disco
R

T
282

283. A segunda lei de Newton para rotações diz que o torque deve ser igual ao momento
de inércia multiplicado pela aceleração angular. O momento de inércia de um disco
(em relação a um eixo passando pelo centro de massa) é dado por:
2π R 2
M 1
I= ∫∫r
0 0
πR 2
rdrdθ = MR 2
2
A segunda lei de Newton é dada por:
1 a 1
τ = − RT = I ( − α ) ⇒ RT = MR 2 ⇒ T = Ma
2 R 2
Diagrama de corpo livre para o bloco: 
T

Fg
283

284. Segunda lei de Newton para o bloco:
T − mg = m( − a ) ⇒ T = m( g − a )
Reunindo a segunda lei de Newton para o disco e a segunda lei de Newton para o bloco,
obtemos:
1 m
Ma = m( g − a ) ⇒ a = g
2 M
m+
2
Portanto, a aceleração do bloco vale
1,2kg m m
a= 9,8 2 = 4,8 2
2,5kg s s
1,2kg +
2
A aceleração angular do disco vale
m
4,8
a s 2 = 24 rad
α= =
R 0,2m s2
284

285. A tensão na corda é dada pela segunda lei de Newton para rotações aplicada ao bloco:
1 1 m
T = Ma = 2,5kg 4,8 2 = 6 N
2 2 s
285

286. Trabalho e energia cinética da rotação
• O trabalho realizado por um torque sobre
uma partícula, sistema de partículas ou corpo
contínuo é dado por:
θ2
W = ∫ τ ⋅ dθ
θ1
• Este trabalho também obedece ao teorema
do trabalho e energia cinética:
1 2 1 2
W = ∆K = Iω final − Iωinicial
2 2
• A potência de um dado torque é dada por:
Pmédia = τ médio ⋅ ωmédia , P = τ ⋅ ω
286

287. Exemplo 10-2
• Uma chaminé cilíndrica começa a tombar
quando sua base é danificada. Trate a
chaminé como uma barra fina de
comprimento L=55m (Figura). Qual é a sua
velocidade angular ω no instante em que faz
um ângulo θ=35º com a vertical?
287

288. y
θ
CM
L
L/2
288

289. Solução
289

290. 290

291. Rolamento, Torque e Momento
Angular
Unidade VII
291

292. Rolamento como uma combinação de
translação e rotação
292

293. A Energia Cinética do Rolamento
• Sendo o rolamento a composição de uma
translação com uma rotação, a energia
cinética do rolamento é composta de duas
parcelas (uma para translação e outra para
rotação):
1 1
K = I CM ω + MvCM
2 2
2 2
293

294. Forças do Rolamento
• Como a força normal e a força gravitacional
atuam no centro de massa do corpo, é preciso
a presença da força de atrito dinâmica para
garantir o corpo movimento.
• Se o corpo está rolando em um plano
horizontal: a = αR
CM
• Caso o corpo esteja rolando em um plano
inclinado:
gsenθ
aCM =
I CM
1+
MR 2 294

295. Exemplo 11-2
• Uma bola uniforme, de massa M=6kg e raio R, rola
suavemente, a partir do repouso, descendo uma
rampa inclinada de ângulo θ=30º.
• (a) A bola desce uma distância vertical h=1,2m para
chegar à base da rampa. Qual é a sua velocidade ao
chegar à base da rampa?
• (b) Quais são o módulo e a orientação da força de
atrito que age sobre a bola quando ele desce a
rampa rolando?
295

296. Solução
296

297. 297

298. 298

299. Momento Angular
• Devemos modificar a definição do momento para
o caso da rotação:   
L=r×p
• O momento angular aponta na direção do eixo de
rotação e seu sentido é dado pela regra da mão
direita aplicada ao vetor posição e momento
linear.
• O momento angular é máximo na situação em
que vetor posição e momento linear são
perpendiculares (movimento circular).
299

300. Eixo de rotação. ˆ
i ˆ
j ˆ
k

 τ = x y z

L px py pz
r

p
τ = r ⋅ p ⋅ sen(θ ) = r⊥ ⋅ p = r ⋅ p⊥
θ é o ângulo entre o vetor posição e o momento.
r⊥
é a componente do vetor posição perpendicular ao momento.
é a componente tangencial do momento
p⊥
300

301. Exemplo 11-4
301

302. e passará a 4m do ponto O. Quais são o módulo e a orientação do momento angular

total em relação ao ponto O do sistema formado pelas duas partículas?
L

p2
r ⊥2
r ⊥1

r2

p1

r1
302

303. Solução
• Como foram dadas as componentes do vetor
posição perpendiculares às direções do
momentos das partículas podemos calcular o
módulo do momento angular de cada
partículas como: l = r p = 2m ⋅ 5kg ⋅ m = 10kg ⋅ m
1 ⊥1 1
2
s 2
m m2
l2 = r⊥ 2 p2 = 4m ⋅ 2kg ⋅ = 8kg ⋅
s s
• O momento angular da primeira partícula
aponta para fora do plano da figura e o
segundo aponta para dentro do plano da
figura (regra da mão direita). 303

304. Como o momento angular da primeira partícula
é maior que o da segunda partícula, o momento
angular total aponta para fora do plano da
figura. O seu módulo é dado por:
m2 m2
L = (10 − 8) kg ⋅ = 2kg ⋅
s s
304

305. Se o corpo, partícula ou corpo contínuo
estiver girando em torno de um eixo
fixo com velocidade angular constante,
podemos relacionar o momento angular
diretamente com o momento de
inércia:
L = Iω
305

306. Segunda Lei de Newton para rotações
• O torque resultante que age sobre a partícula,
sistema de partículas ou corpo contínuo é
igual à derivada em relação ao tempo do
momento angular da partícula, corpo
contínuo ou sistema de partículas.

 dL
τ res =
dt
306

307. Exemplo 11-5
• Na Figura um pinguim de massa m cai, sem
velocidade inicial, do ponto A, a uma distância
horizontal D da origem O de um sistema de
coordenadas x,y,z. (O sentido positivo do eixo
z é para fora do papel.)

• (a) Qual é o momento angular do pinguim
l
em relação ao ponto O?
• (b) Qual é o torque em torno da origem
devido à força gravitacional?
307

308. O
D
308

309. Solução
309

310. 310

311. Exemplo 11-6
• George Washington Gale Ferris, Jr, um engenheiro civil formado no
Instituto Politécnico Rensselaer, construiu a roda gigante original para a
Exposição Mundial de 1893 em Chicago. A roda, uma impressionante
construção para a época, tinha 36 carros de madeira, cada um com a
capacidade de 60 passageiros, em um círculo de raio 38m. A massa de
cada carro ficava em torno de 1,1x104kg. A massa da estrutura da roda
vale 6x105kg estava concentrada no aro de metal que sustentava os
carros. A roda completava uma volta em 2 minutos.
• (a) Estime o módulo do momento angular da roda, cabines e passageiros
quando a roda realizava uma volta completa.
• (b) Se a roda acelerava do repouso até a velocidade desejada em um
intervalo de tempo de 5 segundos, estime o módulo do torque resultante
que age sobre a roda.
311

312. Solução
312

313. 313

314. Conservação do momento angular
• Na ausência de torques externos, o momento
angular de uma partícula, corpo contínuo ou
sistema de partículas é conservado ao longo
do tempo.
 
Linicial = L final
314

315. Exemplo 11-8
• Na Figura, uma barata de massa m caminha
sobre um disco de massa 6m e raio R. O disco
inicialmente gira com velocidade angular
ω=1,5 rad/s no sentido anti-horário. A barata
está inicialmente no raio r=0,8R, mas depois
caminha até a borda do disco. Trate a barata
como uma partícula. Qual é a sua velocidade
angular final?
315

316. ωi
R r
316

317. Solução
317

318. 318

319. Fluidos
Unidade VIII
319

320. Propriedades Básicas dos Fluidos
• Um fluido é um objeto sem rigidez, suas partes podem se mover
umas em relação às outras.
• Dessa forma, para entender um fluido é preciso estudar
quantidades que mostram a variabilidade das diversas partes de
um fluido.
• Uma linha de corrente é a trajetória descrita por um ponto do
fluido.
• A seção transversal do fluido é o corte feito por um plano
atravessando o fluido.
Linha de corrente.
Seção transversal.
320

321. Densidade
• Para medir a inércia de um fluido devemos utilizar a densidade (e
não a massa) do fluido. A densidade é dada pela derivada da massa
(m) em relação ao volume do fluido (V):
∆m
ρ = lim
∆V →0 ∆V
• Em geral, a densidade depende de cada parte do fluido. Entretanto,
temos o caso de um fluido uniforme com a densidade não
apresentando mudança de uma parte para outra do fluido. Neste
caso temos a densidade (uniforme) dada pela razão da massa do
fluido pelo seu volume: m
ρ=
V
• Unidade no S.I.: kg/m3
321

322. Pressão
• Para analisar a causa do movimento devemos utilizar o
conceito de pressão, que é a causa que faz um pequeno
elemento da seção transversal do fluido se mover (ΔA).
A pressão é a derivada da força (F) em relação à área (A)
da seção transversal do fluido:
∆F
p = lim
∆A→0 ∆A
• A força (F) utilizada para definir a pressão aponta na
direção oposta à normal do fluido!
• Para o caso da pressão ser uniforme (não variar ao longo
da seção transversal do fluido), a definição de pressão é
dada por:
• Unidade do S.I.: Pascal (Pa).
F
p=
A
322

323. Exemplo 14-1
• Uma sala de estar tem as dimensões do piso
de 3,5m de largura e 4,2m de espessura e uma
altura de 2,4m.
• (a) Quanto o ar dentro da sala pesa se a
pressão do ar no sala é 1 atm?
• (b) Qual o módulo da força que o ar exerce no
topo da sua cabeça, se você considere que a
área correspondente vale 0,04 m2?
323

324. Solução
324

325. Hidrostática
Princípio de Stevin
• Para um fluido em repouso, sobre a influência da
gravidade da Terra; a pressão depende apenas da
componente perpendicular à seção transversal do
fluido (altura, y, ou profundidade, h) e independe das
componentes paralelas à seção transversal do fluido:
p2 = p1 + ρ ⋅ g ⋅ ( y1 − y2 )
• Em termos da profundidade do fluido, temos (p0 é a
pressão no topo do fluido):
p = p0 + ρ ⋅ g ⋅ h
325

326. Exemplo 14-2
• Um mergulhador novato praticando em uma piscina
inala ar suficiente do seu tanque até encher os
pulmões até mergulhar até uma profundidade L e
retornar à superfície. Ele ignora as instruções e não
exala o ar durante a subida. Quando ele atinge a
superfície, a diferença entre a pressão do ar nos seus
pulmões e a pressão atmosférica é 9,3kPa. De que
profundidade partiu?
326

327. Solução
327

328. Exemplo 14-3
328

329. d
óleo
l
Interface
Água
329

330. Solução
330

331. Princípio de Pascal
• Qualquer variação na pressão nas
extremidades do fluido é transmitida a todas
as partes do fluido de maneira igual:
∆p = ∆pext
• O princípio de Pascal é utilizado no elevador
hidráulico, onde aplicamos uma força
pequena em uma extremidade para obter
uma força grande na outra extremidade:
A 
F2 =  2  F1
A 
 1
331

332. Princípio de Arquimedes
• Quando um objeto está imerso em fluido,
aparece uma força que tenta expelir o objeto
do fluido. Esta força é o empuxo, que segundo
o princípio de Arquimedes é igual ao peso do
líquido deslocado (pelo objeto):
E = g ⋅ mlíquido deslocado = g ⋅ ρ líquido ⋅ Vlíquido deslocado

E
332

333. Exemplo 14-4
333

334. x
y
θ
334

335. Solução
335

336. O módulo do empuxo é dado pelo peso da água deslocada pela prancha:
E = ρ águaVg = 1.024 kg m3 2,5 ⋅10 −2 m 3 ⋅ 9,8 m s 2 = 2,509 ⋅10 2 N
As componentes da força de arrasto são dadas por:

 Fa , x = mgsenθ = 83kg ⋅ 9,8 m s 2 ⋅ sen300 = 406,7 N

 Fa , y = mg cos θ − E = 83kg ⋅ 9,8 m s ⋅ cos 30 − 250,9 N = 453,5 N
2 0

O módulo da força de arrasto é dado por:
Fa = Fa2,x + Fa2, y = 609 N
A direção da força de arrasto é dada pelo seguinte ângulo:
Fa , y 453,5 N
tan φ = = = 1,11
Fa , x 406,7 N
φ = 48o
336

337. Flutuação
• Para que um objeto flutue é preciso que a força
gravitacional equilibre o empuxo exercido pelo
fluido: E=F g

E

Fg
• Se a força gravitacional é maior que o empuxo, o
objeto afunda dentro do fluido. Caso contrário, o
objeto é expelido do fluido!
337

338. Exemplo 14-5
338

339. Solução
339

340. 340

341. Dinâmica dos fluidos
Equação da Continuidade
• Supondo que o fluido é incompressível (sua
densidade é uniforme e não muda ao longo
do tempo) e não possui vazamentos; temos a
seguinte equação para a velocidade (da linha
de corrente) e área (da seção transversal do
fluido):
A1 ⋅ v1 = A2 ⋅ v2
341

342. Exemplo 14-6
• A água cai de uma torneira afinando sua seção
transversal quando cai. A área da seção
transversal na boca da torneira é A0=1,2cm2 e a
área da seção transversal na parte de baixo é
A=0,35cm2. A boca da torneira e o nível
inferior estão separados por uma distância
h=45mm. Qual é a vazão volumétrica na boca
da torneira?
342

343. Solução
343

344. 344

345. Equação de Bernoulli
• Com o fluido se movendo, devemos substituir
o princípio de Stevin pela equação de
Bernoulli (expressão da conservação de
energia):
1 1
p1 + ρ ⋅ g ⋅ y1 + ⋅ ρ ⋅ v12 = p2 + ρ ⋅ g ⋅ y2 + ⋅ ρ ⋅ v2
2
2 2
345

346. Exemplo 14-7
346

347. Solução
347

348. 348

349. Exemplo 14-8
• No Velho Oeste, um bandido acerta um tiro
em um tanque de água com a tampa aberta,
criando um buraco a uma profundidade h
abaixo da superfície da água. Qual é a
velocidade v da água que está saindo do
tanque?
349

350. Solução
350

351. Temperatura, Calor e Primeira
Lei da Termodinâmica
Unidade IX
351

352. Introdução
• A termodinâmica trata da dinâmica que um sistema possui ao
modificar o arranjo dos seus graus de liberdade internos.
• Para medir a agitação dos graus de liberdade internos,
usamos a temperatura. Quente significa que o sistema está
muito agitado e frio é a situação oposta.
• O calor é a energia transferida para o sistema que modifica os
graus de liberdade internos, sem modificar os graus de
liberdades externos; fazendo a temperatura do sistema
variar.
• Trabalho é a energia transferida para o sistema capaz de
modificar seus graus de liberdade externos.
352

353. Lei Zero da Termodinâmica
• Se um corpo está em equilíbrio
termodinâmico com um certo corpo e
também em equilíbrio termodinâmico com
um terceiro corpo. Então o segundo e o
terceiro corpos mencionados estarão em
equilíbrio entre si.
• A temperatura é portanto uma função do
estado do sistema!
353

354. Temperatura
• Existem várias escalas de temperatura, mas três são mais
usadas no dia-a-dia.
• A escala Kelvin é a mais utilizada em artigos científicos. Seu
zero é a menor temperatura que um sistema pode atingir.
• A escala Celsius é muito utilizada na medicina. Seu zero é o
ponto de congelamento da água. O valor de 100 é atribuído
para o ponto de ebulição da água.
• A escala Fahrenheit modifica os valores do ponto de
congelamento da água para 32 e o ponto de ebulição para
212. Muito utilizada nos Estados Unidos.
354

355. Escalas de Temperatura
• A relação entre a escala Celsius, Tc, e Kelvin, T;
é dada por:
TC = T − 273,15
• A relação entre a escala Celsius e Fahrenheit,
TF, é dada por:
9
TF = 32 + TC
5
355

356. Exemplo 18-1
• Suponha que você encontre velhos notas
científicas que descrevem uma escala de
temperatura chamada Z em que o ponto de
ebulição da água vale é 650Z e o ponto de
congelamento é -14oZ. A qual temperatura da
escala Fahrenheit uma temperatura de -98oZ
irá corresponder? Assuma que a escala Z é
linear, ou seja, o valor de um grau na escala Z
é o mesmo em todo o intervalo da escala.
356

357. Solução
357

358. Dilatação Térmica
• Quando um corpo sofre um aumento de
temperatura, seu comprimento cresce
proporcional ao incremento na temperatura:
∆L = Lα∆T
• O coeficiente de dilatação linear é α.
• O volume do corpo também cresce com o
aumento de temperatura:
∆V = Vβ∆T
• O coeficiente de dilatação volumétrica é dado
por: β = 3α
358

359. Exemplo 18-2
Em um dia quente em Las Vegas, um caminhão
carregou 37.000L de óleo diesel. Ele encontrou
tempo frio no caminho até Payson, Utah, onde a
temperatura era 23K abaixo da temperatura em
Las Vegas, onde ele entregou sua carga
completa. Quantos litros ele entregou? O
coeficiente de dilatação volumétrica do óleo
diesel é 9,5x10-4oC-1, e o coeficiente de dilatação
linear do aço do caminhão é 11x10-6oC-1?
359

360. Solução
360

361. Capacidade Calorífica
• Quando calor é injetado em um sistema, sua
temperatura aumenta. A capacidade
calorífica, C, é o fator entre o calor injetado,
Q, e a variação de temperatura, ΔT:
Q = C ⋅ ∆T = C ⋅ (T f − Ti )
• A capacidade calorífica é constante para a
maioria dos materiais sólidos e líquidos.
361

362. Calor Específico
• Para considerar somente a substância, introduzimos o calor
específico; que é a razão entre a capacidade calorífica e a
massa do material, m:
Q = m ⋅ c ⋅ ∆T = m ⋅ c ⋅ (T f − Ti )
• O calor específico é constante para os materiais sólidos ou
líquidos.
• O calor específico molar é dado em termos da quantidade de
moles (número de moléculas dividido pelo número de
Avogrado):
Q = n ⋅ cmolar ⋅ ∆T
• Unidade do S.I.: J/kg K ou J/mol K.
362

363. Calor Latente
• Durante uma transição de fases, a temperatura do
material não muda até uma fase (sólida, líquida,
gasosa, etc.) ter se convertido na outra.
• O calor absorvido,Q, durante a transição é dado por:
Q = m⋅ L
• A massa do material é m, enquanto L é o calor
latente da substância para a transição considerada
(calor de transformação).
• Unidade do S.I.: J/kg.
363

364. Exemplo 18-3
(a) Quanto de calor deve ser absorvido por gelo
de massa m=720g à -10oC para se
transformar em água líquida a 15oC?
(b) Se você fornecer ao gelo somente 210kJ de
energia (em forma de calor), qual é o estado
final do gelo e sua temperatura?
364

365. Solução
365

366. 366

367. 367

368. Trabalho
• O trabalho mecânico realizado por um gás é
dado pela integral da pressão contra o volume
do gás:
Vf
W= ∫ p ⋅ dV
Vi
• Esta é a energia necessária para modificar o
volume de um gás (variável externa).
368

369. Primeira Lei da Termodinâmica
• A diferença entre o calor introduzido em um sistema e o trabalho
realizado pelo sistema independe do processo pelo qual o sistema passou
e é igual a variação da energia interna do sistema (energia devida à
agitação dos graus de liberdade internos):
∆Eint = Q − W = Eint, f − Eint,i
• Para variações diferenciais, temos:
• A energia interna é função do estado do sistema! Mas o calor e o trabalho
não são funções do estado do sistema (dependem do processo que o
sistema passou)!
dEint = dQ − dW
369

370. Processos Termodinâmicos
• Processo adiabático: É aquele (tão rápido) em que não há
trocas de calor, Q=0.
• Processo isovolumétrico: É aquele em que o volume do
sistema é mantido constante. O trabalho realizado pelo
sistema é nulo, W=0.
• Processo isobárico: É aquele em que a pressão sobre o
sistema é mantida constante. Neste caso W =p ⋅∆ V
• Processo isotérmico: É aquele em que a temperatura é
mantida constante.
370

371. Exemplo 18-5
Considere que 1kg de água líquida à 100oC pode ser
convertida em vapor à 100oC por evaporação na
pressão atmosférica padrão. O volume da água varia de
1x10-3m3 como água líquida para 1,671m3 como gás.
(a)Quanto trabalho o sistema faz durante esse
processo?
(b) Quanto energia é transferida para o sistema em
forma de calor durante o processo?
(c) Qual é a mudança na energia interna do sistema
durante o processo?
371

372. Solução
372

373. 373

374. Imagens
Unidade X
374

375. Dois tipos de imagens
• Imagem Real: É a imagem formada do lado
oposto ao que está o objeto, considerando o
espelho como origem.
• Imagem Virtual: É a imagem formado do
mesmo lado em que está o objeto,
considerando o espelho como origem.
375

376. Leis da reflexão
• Quando a luz incide em um meio, podemos
distinguir o ângulo de incidência (com a
normal à interface, θi) e o ângulo de reflexão
(com a normal à interface, θr).
θi θr
376

377. • O ângulo de incidência e de reflexão são
iguais!
• A imagem pode ser formada pelos raios ou
por seus prolongamentos.
• A imagem é real, se é formada do mesmo lado
do objeto (com a interface na origem).
• A imagem é virtual, se formada do lado
oposto ao objeto (com a interface na origem).
• A imagem pode ser ampliada ou reduzida.
• Para obter a imagem fazemos os encontros
dos raios que vêm das extremidades do
objeto. 377

378. Espelhos Planos
• Os espelhos são superfícies que refletem a
maioria da luz que incidem sobre elas!
• Um espelho plano é um espelho com uma
superfície plana.
Objeto
Imagem
378

379. • Em um espelho plano a imagem não
apresenta ampliação!
• Em um espelho plano a imagem é virtual!
• Em um espelho plano, a distância da imagem
até o espelho é a mesma distância do objeto
até o espelho!
379

380. Espelhos Esféricos
• É o espelho cuja superfície é uma porção de
uma esfera.
• Pode ser côncavo, quando a superfície
refletora é formada pela parte de dentro da
esfera.
• Pode ser convexo, quando a superfície
refletora é formada pela parte de fora da
esfera.
380

381. Espelho convexo Espelho côncavo
• Os espelhos esféricos têm a propriedade de
convergir/divergir os raios que vêm do infinito (paralelos
entre si) para o foco do espelho.
• No caso do espelho côncavo, o espelho converge os raios
para o foco. A distância focal é positiva (foco na frente do
espelho).
• No caso do espelho convexo, o espelho diverge os raios do
foco. A distância focal é negativa (foco atrás do espelho).
381

382. • Considerando a distância do objeto ao
espelho como p, a distância da imagem ao
objeto como i e a distância focal como f.
Temos a seguinte equação para os espelhos
esféricos: 1 1 1
+ =
p i f
• O módulo da distância focal é o metade do
raio do espelho: f = r
2
• A altura da imagem, , e altura do objeto h;
h ´
estão relacionadas por:
´
h i
• h
=−
p
382

383. • Em um espelho esférico a imagem pode ser
virtual ou real.
• Em um espelho esférico a imagem pode ser
reduzida ou ampliada.
• Podemos prever esses comportamentos,
localizando a posição da imagem em relação
ao foco do espelho e seu centro através do
encontro dos raios de luz (ou dos seus
prolongamentos).
383

384. Exemplo 34-1
384

385. Solução
385

386. 386

387. Leis da Refração
• A refração acontece quando os raios de luz
atravessam de um meio para outro!
θ1
θ2
• Podemos distinguir o ângulo de incidência, θ1,
e o ângulo de refração, θ2.
387

388. Lei de Snell
• O índice de refração é a razão da velocidade
da luz no vácuo pela velocidade da luz no
meio: n = c
v
• Os ângulos de incidência e refração são
relacionados com os índices de refração do
meio 1, n1, e meio 2, n2:
n1sen(θ1 ) = n2 sen(θ 2 )
388

389. Exemplo 33-3
(a)Na Figura, um feixe de luz monocromático
reflete e refrata no ponto A de uma interface de
um material 1 com índice de refração n1=1,33
com um material 2 de índice de refração
n2=1,77. O feixe incidente faz um ângulo de 50º
com a interface. Qual é o ângulo de reflexão no
ponto A? Qual é o ângulo de refração nesse
ponto?
389

390. (b) A luz que penetra no material 2 no ponto A atinge o
ponto B da interface do material 2 com o material 3,
que é o ar, como mostrado na Figura. A interface onde
está o ponto B é a paralela à interface onde está o
ponto A. Em B, parte da luz reflete e outra parte entra
no ar. Qual é o ângulo de reflexão? Qual é o ângulo de
refração no ar?
Meio 1
A
Meio 2
B Meio 3
390

391. Solução
391

392. 392

393. Reflexão Interna Total
• Para ângulos maiores que o ângulo crítico, θc,
a luz é totalmente refletida pela interface
entre os dois meios. Neste caso a refração não
existe, apenas a reflexão! O ângulo crítico é
dado por:
 n2 
θ C = sen  
−1
n 
 1
393

394. Exemplo 33-5
A proposta de um anel de diamantes, claro, é brilhar. Parte da arte de
cortar um diamante é garantir que toda luz incidente sobre essas
superfícies é refletida, garantido o brilho do diamante. A figura mostra
um corte transversal de um diamante brilhante, com um raio de luz
entrando no ponto A da superfície de cima. Neste tipo de corte, as
superfícies de cima e de baixo tem normais que fazem um ângulo de
48,84º. No ponto B, pelo menos parte da luz é refletida e retorna para
a superfície de cima, mas parte refrata e pode deixar o diamante.
Considere um raio de luz incidente com um ângulo θ1=40o em A. A luz
escapa se existe ar (n4 =1) sob a superfície de baixo? A luz escapa se
uma superfície gordurosa (n4 =1,63) cobre a superfície? O índice de
refração do diamante é ndia =2,419.
394

395. θ1
θ2
θ3
48,84o
θ4
395

396. Solução
396

397. 397

398. Superfícies Refratoras Esféricas
• Se a interface entre os dois meios é uma porção de
esfera, temos uma superfície refratora esférica.
• Se a superfície é côncava, o raio de curvatura é
negativo. Se a superfície é convexa, o raio de
curvatura é positivo.
• A superfície refratora esférica pode formar uma
imagem de um objeto. A imagem pode ser real, se
fica do lado oposto ao objeto (em relação à
interface); ou virtual, se fica do mesmo lado do
objeto (em relação à interface).
398

399. O C
I
• Sendo p, a distância do objeto até a interface,
e i, a distância da imagem até a interface;
temos:
n1 n2 n2 − n1
+ =
p i r
399

400. Exemplo 34-2
Um mosquito jurássico foi descoberto dentro de
uma pedra de âmbar, que tem índice de
refração 1,6. Uma superfície do âmbar é
côncava e tem raio de curvatura 3mm. A cabeça
do mosquito está no eixo central da pedra de
âmbar e, quando vista ao longo do eixo,
aparenta estar enterrada a uma distância de
5mm dentro do âmbar. Qual é a verdadeira
distância em que o mosquito está enterrado?
400

401. Solução
Como temos uma superfície refratora côncava,
o raio de curvatura é negativo e vale r=-3mm.
Foi dada a distância da imagem, que é negativa;
já que o mosquito está do mesmo lado que a
sua imagem (dentro do âmbar): i=-5mm. Dessa
forma, a distância do mosquito até o vértice da
superfície refratora esférica é dada através da
equação:
401

402. 402

403. Lentes Delgadas
• Se unirmos duas superfícies refratoras
esféricas separadas de uma distância muito
pequena, temos uma lente delgada.
• As lentes delgadas podem formar imagens
através da convergência dos raios (lente
convergente) ou do prolongamento dos raios,
ou seja, da divergência dos raios (lente
divergente).
403

404. Lente convergente Lente divergente
• Temos a seguinte equação para as imagens
das lentes delgadas:
1 1 1
+ =
p i f
404

405. Equação do Fabricante de Lentes
• A distância focal da lente é dada por (o meio
que envolve a lente é o ar):
1 1 1
= ( n − 1)  − 
r r 
f  1 2
• Se a distância focal é positiva, a lente é
convergente.; caso contrário, a lente é
divergente.
• A ampliação da lente é dada por:
h´ i
m= =−
h p 405

406. Exemplo 34-4
Um louva-a-deus está em um eixo central de uma lente
delgada simétrica, a 20cm da lente. A ampliação do
louva-a-deus vale m=-0,25, e o índice de refração do
material da lente é 1,65.
(a)Determine o tipo de imagem produzida pela lente, o
tipo de lente, se o louva-a-deus está do mesmo lado ou
do lado oposto ao ponto focal, de que lado da lente a
imagem aparece, e se a imagem é invertida.
(b)Quais são os dois raios de curvatura da lente?
406

407. Solução
407

408. 408

409. 409

410. Instrumentos Óticos
O olho
• O sistema córnea-cristalino dos olhos focaliza a luz sobre a retina, onde
ela é sentida pelos bastonetes e cones que enviam a informação ao longo
do nervo ótico para o cérebro.
• Quando o olho está relaxado, o comprimento focal do sistema córnea-
cristalino está em torno de 2,5 cm, que é a distância até a retina.
• Quando os objetos são colocados próximos aos olhos o cristalino varia de
forma a diminuir o comprimento focal total, de tal modo que a imagem
permaneça focalizada pela retina.
• A menor distância para a qual a imagem pode ser focalizada na retina é
chamada de ponto próximo, tipicamente em torno de 25 cm.
410

411. • O tamanho aparente de um objeto depende do tamanho
da imagem na retina e, portanto, maior o tamanho aparente
do objeto.
•Quanto mais próximo o objeto, maior sua imagem na retina
e, portanto, maior o tamanho aparente do objeto.
411

412. Lupa
• Uma lupa simples cria uma imagem virtual cujo tamanho
angular é maior do que o tamanho angular θ produzido
θ′
pelo próprio objeto a uma distância igual a 25 cm , a distância
mais próxima do olho para que se tenha um visão
confortável.
• A ampliação angular produzida por uma lupa simples é dada
pela razão entre o tamanho angular da imagem virtual e o
tamanho angular do mesmo objeto nessa distância:
θ′
M=
θ
• Para uma lupa simples com distância focal f, obtemos M=(25
cm/f).
412

413. Microscópio Ótico
• No microscópio ótico a lente da objetiva forma uma
primeira imagem no tubo do instrumento e a ocular
forma uma imagem virtual final, geralmente no
infinito, da primeira imagem.
• A ampliação angular é dada em termos das
distâncias focais da objetiva, f1 e da ocular f2 e da
distância da primeira imagem até a objetiva:
M=
( 25 cm) ⋅ s1′
f1 f2
413