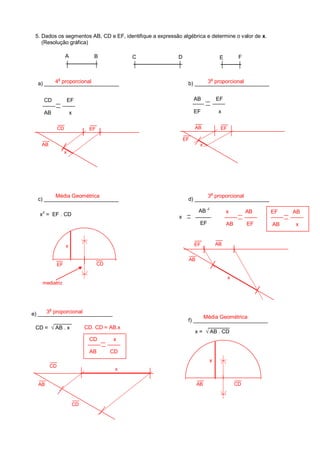
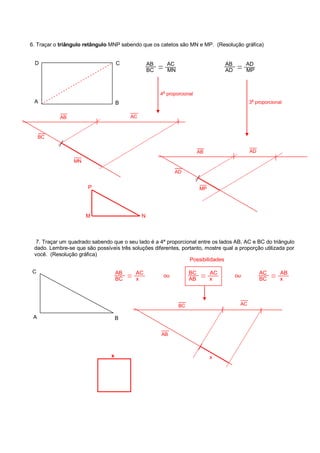
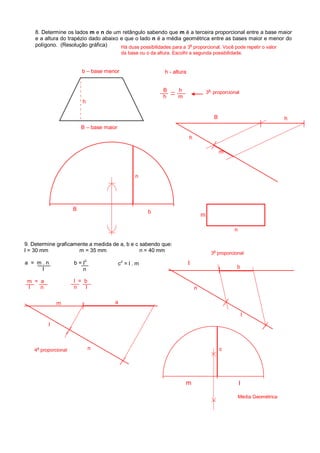
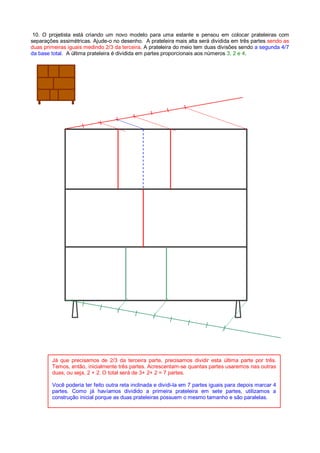
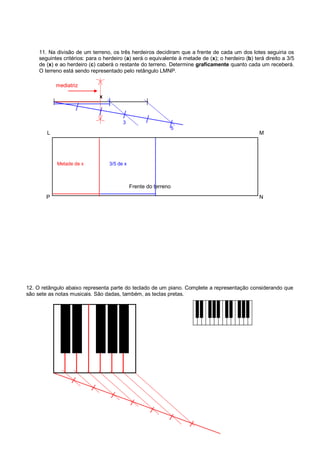
1. O documento apresenta 12 exercícios de geometria que envolvem divisão de segmentos em proporções dadas e construção de figuras geométricas. 2. Os exercícios devem ser resolvidos graficamente e envolvem noções como proporcionalidade, razão, média geométrica e triângulos retângulos. 3. A resolução é feita passo a passo com a explicação do raciocínio e da construção geométrica realizada.

1. Desenho Geométrico
Módulo 1
9o
Ano
Departamento de Desenho e Artes Visuais
Profas
Lourdes Ferreira, Cristina Salles e
Erika Menezes
Desenho - Campus Humaitá II
2014

2. AB = 2
BC 3
1. Divida o segmento AC em partes
proporcionais. (Resolução gráfica)
A C
2. Divida o segmento AB em partes
proporcionais aos segmentos a e b dados.
(Resolução gráfica)
EXERCÍCIOS - 1a
Certificação 9o
Ano/2014 - Profas
Lourdes, Cristina e Erika
3. Divida cada segmento abaixo na proporção pedida. (Resolução gráfica)
a) LM é igual a 5/9 de AB
A
B
C
D
4. Traçar o retângulo ABCD sabendo que os seus lados estão na razão 2/3. (Resolução gráfica)
LM – semiperímetro do retângulo
L M
b) EF é igual a 3/8 de CD
a b
A B

3. CD EF
AB x
b) _________________________
AB EF
EF x
AB
2
x
EF
C D E FA B
5. Dados os segmentos AB, CD e EF, identifique a expressão algébrica e determine o valor de x.
(Resolução gráfica)
x
2
= EF . CD
a) _________________________
d) _________________________c) _________________________
f) _________________________e) _________________________
CD = √ AB . x x = √ AB . CD

4. 6. Traçar o triângulo retângulo MNP sabendo que os catetos são MN e MP. (Resolução gráfica)
A
D
B
C
7. Traçar um quadrado sabendo que o seu lado é a 4ª proporcional entre os lados AB, AC e BC do triângulo
dado. Lembre-se que são possíveis três soluções diferentes, portanto, mostre qual a proporção utilizada por
você. (Resolução gráfica)
A
C
B
AB AC
BC MN
AB AD
AD MP

5. 8. Determine os lados a e b de um retângulo sabendo que a é a terceira proporcional entre a base maior e
a altura do trapézio dado abaixo e que o lado b é a média geométrica entre as bases maior e menor do
polígono. Monte a terceira proporcional antes de resolver a questão. (Resolução gráfica)
a = m . n
l
b = l2
n
9. Determine graficamente a medida de a, b e c sabendo que:
l = 30 mm m = 35 mm n = 40 mm
c
2
= l. m

6. 10. O projetista está criando um novo modelo para uma estante e pensou em colocar prateleiras com
separações assimétricas. Ajude-o no desenho. A prateleira mais alta será dividida em três partes sendo as
duas primeiras iguais medindo 2/3 da terceira. A prateleira do meio tem duas divisões sendo a segunda 4/7
da base total. A última prateleira é dividida em partes proporcionais aos números 3, 2 e 4.

7. 11. Na divisão de um terreno, os três herdeiros decidiram que a frente de cada um dos lotes seguiria os
seguintes critérios: para o herdeiro (a) será o equivalente à metade de (x); o herdeiro (b) terá direito a 3/5
de (x)e ao herdeiro (c) caberá o restante do terreno. Determine graficamente quanto cada um receberá.
O terreno está sendo representado pelo retângulo LMNP.
x
12. O retângulo abaixo representa parte do teclado de um piano. Complete a representação considerando que
são sete as notas musicais. São dadas, também, as teclas pretas.
L M
NP
Frente do terreno

8. AB = 2
BC 3
1. Divida o segmento AC em partes
proporcionais. (Resolução gráfica)
A C
2. Divida o segmento AB em partes
proporcionais aos segmentos a e b dados.
(Resolução gráfica)
a b
A B
3. Divida cada segmento abaixo na proporção pedida. (Resolução gráfica)
a) LM é igual a 5/9 de AB b) EF é igual a 3/8 de CD
A
B
C
D
4. Traçar o retângulo ABCD sabendo que os seus lados estão na razão 2/3. (Resolução gráfica)
LM – semiperímetro do retângulo
L M
EXERCÍCIOS - GABARITO 9o
Ano/2014 - Profas
Lourdes, Cristina e Erika
AB = BC
2 3
B
a
b
9
5
L
M
8
3
F
E 
Semiperímetro = metade da soma dos
lados do polígono
Consideramos um dos lados igual a 2
unidades e o outro igual a 3 unidades.
Total = 5 unidades2
3 A
B C
D
AB BC

9. CD EF
AB x
b) _________________________
AB EF
EF x
AB
2
x
EF
C D E FA B
5. Dados os segmentos AB, CD e EF, identifique a expressão algébrica e determine o valor de x.
(Resolução gráfica)
x
2
= EF . CD
a) _________________________
d) _________________________c) _________________________
f) _________________________
CD = √ AB . x
x = √ AB . CD
4
a
proporcional 3
a
proporcional
3
a
proporcionalMédia Geométrica
Média Geométrica
x
AB
x
CD
AB
EF
EF AB
x AB
AB EF
EF AB
AB x
x
x
EF
EFAB
CDAB
CD. CD = AB.x
CD x
AB CD
x
AB
CD
CD
x
CDEF
mediatriz
e) _________________________3
a
proporcional

10. 6. Traçar o triângulo retângulo MNP sabendo que os catetos são MN e MP. (Resolução gráfica)
A
D
B
C
7. Traçar um quadrado sabendo que o seu lado é a 4ª proporcional entre os lados AB, AC e BC do triângulo
dado. Lembre-se que são possíveis três soluções diferentes, portanto, mostre qual a proporção utilizada por
você. (Resolução gráfica)
A
C
B
AB AC
BC MN
AB AD
AD MP
AB
BC
AC
MN
AB
AD
MP
AD
M N
P
3
a
proporcional
4a
proporcional
AB AC
BC x
Possibilidades
BC AC
AB x
AC AB
BC x
ou ou
x
BC
AB
x
AC

11. 8. Determine os lados m e n de um retângulo sabendo que m é a terceira proporcional entre a base maior
e a altura do trapézio dado abaixo e que o lado n é a média geométrica entre as bases maior e menor do
polígono. (Resolução gráfica)
h - altura
B – base maior
b – base menor
h
B h
h m
m
B
h
h
n
bB
n
m
9. Determine graficamente a medida de a, b e c sabendo que:
l = 30 mm m = 35 mm n = 40 mm
a = m . n
l
b = l
2
n
c
2
= l . m
m = a
l n
l = b
n l
m
l
n
a
l
n
b
c
3
a
proporcional
Média Geométrica
l
lm
3
a
proporcional
Há duas possibilidades para a 3
a
proporcional. Você pode repetir o valor
da base ou o da altura. Escolhi a segunda possibilidade.
4a
proporcional

12. 10. O projetista está criando um novo modelo para uma estante e pensou em colocar prateleiras com
separações assimétricas. Ajude-o no desenho. A prateleira mais alta será dividida em três partes sendo as
duas primeiras iguais medindo 2/3 da terceira. A prateleira do meio tem duas divisões sendo a segunda 4/7
da base total. A última prateleira é dividida em partes proporcionais aos números 3, 2 e 4.
Já que precisamos de 2/3 da terceira parte, precisamos dividir esta última parte por três.
Temos, então, inicialmente três partes. Acrescentam-se quantas partes usaremos nas outras
duas, ou seja, 2 + 2. O total será de 3+ 2+ 2 = 7 partes.
Você poderia ter feito outra reta inclinada e dividi-la em 7 partes iguais para depois marcar 4
partes. Como já havíamos dividido a primeira prateleira em sete partes, utilizamos a
construção inicial porque as duas prateleiras possuem o mesmo tamanho e são paralelas.

13. 12. O retângulo abaixo representa parte do teclado de um piano. Complete a representação considerando que
são sete as notas musicais. São dadas, também, as teclas pretas.
x
11. Na divisão de um terreno, os três herdeiros decidiram que a frente de cada um dos lotes seguiria os
seguintes critérios: para o herdeiro (a) será o equivalente à metade de (x); o herdeiro (b) terá direito a 3/5
de (x) e ao herdeiro (c) caberá o restante do terreno. Determine graficamente quanto cada um receberá.
O terreno está sendo representado pelo retângulo LMNP.
L M
NP
Frente do terreno
mediatriz
Metade de x 3/5 de x
3
5