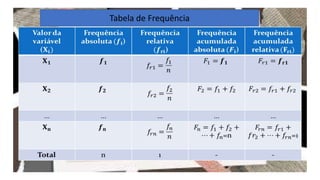
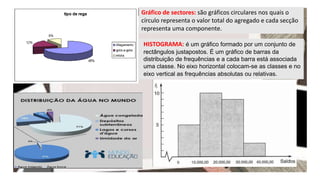
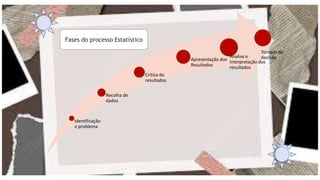
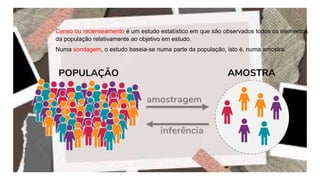
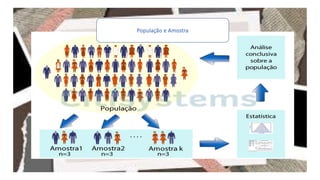
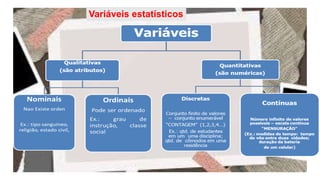
O documento aborda a estatística como um ramo da matemática, detalhando suas aplicações na coleta, análise e interpretação de dados para a tomada de decisões. Apresenta conceitos fundamentais como população, amostra, variáveis estatísticas e tipos de escalas, além de discutir a importância da estatística descritiva e da inferência estatística. Também explora a construção de gráficos e tabelas de frequência, essenciais na visualização de dados.

1. Estatística
Agata Marques

2. A Estatística é um ramo da Matemática que possui instrumentos apropriados para recolher,
organizar, descrever, analisar e interpretar um conjunto de dados, possibilitando a sua utilização
na tomada de decisões.
por exemplo: as empresas precisam de informações para tomar decisões; parte dessas
informações será estatística. nesta tomada de decisões: o principal papel da estatística é
fornecer-lhes os métodos para obter e converter dados (valores, fatos, observações, medições)
em informações úteis.
Definição da Estatística

3. Áreas da Estatística:
A estatística descritiva é a etapa inicial da análise utilizada para organizar, resumir e
representar os dados.
A inferência estatística consiste de procedimentos para fazer generalizações sobre as
características de uma população a partir da informação contida na amostra.
Para isso, é necessário o recurso a Teoria das Probabilidades na qual a inferência
estatística se baseia fortemente.

4. Identificação
o problema
Recolha de
dados
Crítica do
resultados
Apresentação dos
Resultados
Analise e
interpretação dos
resultados
Tomada de
decisão
Fases do processo Estatístico

5. População: Conjunto de elementos com alguma característica em
comum a qual se pretende estudar.
Exemplo: Pessoas, animais, plantas…
Aos elementos da população chamamos de unidades estatísticas.
Uma população pode ser finita ou infinita. Por isso, o estudo é feito
sobre alguns elementos retirados da população, constituindo aquilo a
que se chama uma amostra.
Amostra é um subconjunto finito da população que se supõe representativa
desta e que se observa com o objetivo de tirar conclusões para a população de
onde foi recolhida.
Dimensão ou tamanho da amostra: é o número de dados da
amostra. Representa-se por n.
N- da representa a dimensão População.
Amostragem: É o processo de coleta das informações de parte da
população, chamada
amostra, mediante métodos adequados de seleção destas unidades.
Introdução: Conceitos fundamentais

6. Censo ou recenseamento é um estudo estatístico em que são observados todos os elementos
da população relativamente ao objetivo em estudo.
Numa sondagem, o estudo baseia-se numa parte da população, isto é, numa amostra.

7. População e Amostra

8. Exercício:
Dadas as seguintes expressões abaixo, coloque P para aquelas que dizem
respeito a população e A para amostra:
a) Universo [ ]
b) UCT [ ]
b) inspeção de cada artigo fabricado [ ]
c) realizar um censo [ ]
d) julgar a qualidade de um embarque de frutas inspecionando vários cestos
da remessa [ ]
e) a idade de cada governador de Estado
f) um levantamento de 500 estudantes de uma faculdade com 2.000 alunos

9. Tipo de dados estatísticos e Escala de medidas estatísticas
o Nominal.
o Ordinal
o Intervalo
o Razão
 Escala Nominal.
 Escala Ordinal
 Escala Intervalo
 Escala Razão
Tipos de escalas ou Os níveis de mensuração são representados por diferentes
tipo de escalas.
 Nominal – Usa números como rótulos para identificar e classificar objetivos,
indivíduos ou objetivos. Exemplos: Matrículas de automóveis,
códigos postais, estado civil.
 Ordinal - É uma escala de ranqueamento. Coloca o objeto em uma categoria
predeterminada que a ordena de acordo com algum critério.
Exemplos: Idade, faixa de renda, importância, etc.
Nota
O nível de ordinal fornece informações sobre a ordenação mas não indica a
magnitude das diferenças entre os valores
 Exemplos: Instrumentos de pesagem.

10. Existem diferentes classes de variáveis estatísticas
Das variáveis estatísticas referidas umas são de natureza quantitativa e outras de natureza qualitativa.
Variável estatística quantitativa é uma variável que é suscetível de medição. 2
Exemplos: número de irmãos, a altura de uma pessoa e o rendimento familiar.
Variável estatística qualitativa é uma variável que assume diversas modalidades, categorias ou outras
características, não suscetíveis de medição, mas sim de classificação.
Exemplos: a cor de pele, a cor do cabelo, o estado civil e o sexo.
As variáveis estatísticas de natureza quantitativa podem ainda ser discretas ou contínuas.
As variáveis discretas são aquelas em que entre dois valores a variável não pode tomar todos os valores
intermédios.
Exemplos: número de irmãos e número de automóveis.
As variáveis contínuas são aquelas em que entre dois valores a variável pode tomar todos os valores intermédios.

11. Variáveis estatísticos

12. Exercício:
Dadas as seguintes expressões abaixo, coloque P para aquelas que dizem
respeito a população e A para amostra:
a) Universo [ ]
b) UCT [ ]
b) inspeção de cada artigo fabricado [ ]
c) realizar um censo [ ]
e) A idade de cada governador de Estado
f) um levantamento de 500 estudantes de uma faculdade com 2.000 alunos

13. Exercícios
Classifique as variáveis abaixo:
a) Número de filhos dos funcionários de uma escola.
b) Altura dos estudantes da turma A do Ensino Fundamental de uma escola.
c) Cor dos cabelos dos alunos de uma faculdade.
d) Salário dos professores de uma escola.
e) Número de indivíduos nas famílias dos moradores de um conjunto
residencial.
f) Estado civil dos funcionários de uma escola.
g) Comprimento dos pregos produzidos por uma máquina.
h) Número de peças defeituosas fabricadas por uma máquina diariamente.

14. Definição: Considere-se uma população( de dimensão N) ou uma amostra (de dimensão n) de
indivíduos com característica que apresenta p modalidades observadas 𝑋1, 𝑋2, … , 𝑋𝑝
 Dá-se o nome de distribuição de frequências ao conjunto de todos os valores ou modalidades
de uma variável.
 Chama-se frequência absoluta de 𝒙𝒊, e representa-se por 𝒇𝒊, ao número de vezes que este
valor é observado.
 A frequência relativa de 𝒙𝒊, representa-se por 𝒇𝒓𝒊, é definida pelo quociente entre frequência
absoluta e a dimensão da amostra.
𝒇𝒓𝒊 =
𝒇𝒊
𝒏
, em que 𝑓𝑖 = 𝑛 e 𝑓𝑟𝑖 = 1
 As frequências acumuladas são a soma de número de ocorrências para os valores de variável
inferiores ou iguais ao valor dado.
Frequências acumuladas absolutas
𝐹𝑖 = 𝑓1 + 𝑓2 + ⋯ + 𝑓𝑖
Frequências acumuladas relativas
𝐹𝑟𝑖 = 𝑓𝑟1 + 𝑓𝑟2 + ⋯ + 𝑓𝑟𝑖
Distribuição de frequências

15. Tabela de Frequência

16. Gráfico de barras
Ao construirmos um gráfico de barras, devemos ter em atenção o seguinte:
1º O gráfico deve ter um título;
2º Num eixos colocam-se os dados a ser estudados;
3º No outro eixo colocam-se as frequências absolutas (ou as relativas);
4º As barras devem ter todas a mesma largura;
5º O espaço entre as barras deve ser sempre igual;
6º O comprimento de cada barra deve ser direitamente proporcional á frequência que ilhe
corresponde.
Gráficos circulares
Ao construirmos um gráfico circular, devemos ter em atenção o seguinte:
1º O gráfico deve ter um título;
2º Utiliza se frequência relativa;
3º A amplitude de cada setor é proporcional á frequência correspondentes;
4º Efeito a legenda por setor;

17. Tipos de gráficos
GRÁFICO DE LINHAS- Os valores da variável
apresentada estão unidos por segmentos de linha. É
muito utilizado para representar a evolução da
variável ao longo do tempo
Gráfico de barras múltiplas ou sobrepostas- valores de
diferentes variáveis no mesmo período.

18. Gráfico de sectores: são gráficos circulares nos quais o
círculo representa o valor total do agregado e cada secção
representa uma componente.
HISTOGRAMA: é um gráfico formado por um conjunto de
rectângulos justapostos. É um gráfico de barras da
distribuição de frequências e a cada barra está associada
uma classe. No eixo horizontal colocam-se as classes e no
eixo vertical as frequências absolutas ou relativas.

19. Exercícios

20. Exercício
a. Estude a variavel
de estudo.
b. Cria a tabela de
frequencia.
c. Crontrua o grafico
de barra.

21. Obrigada