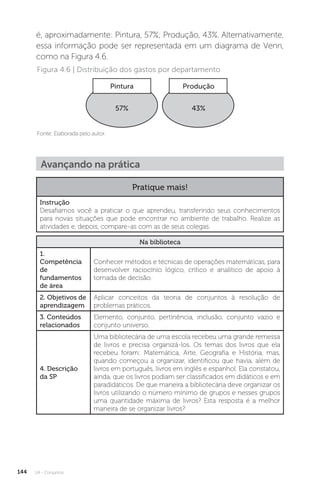
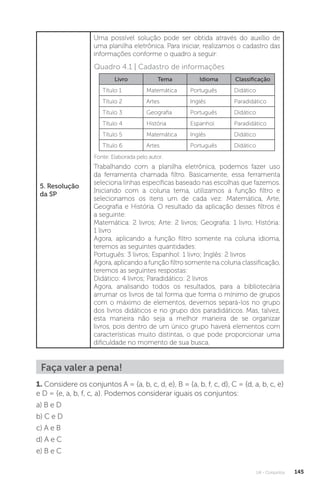
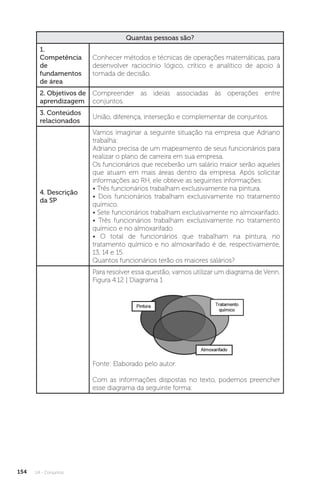
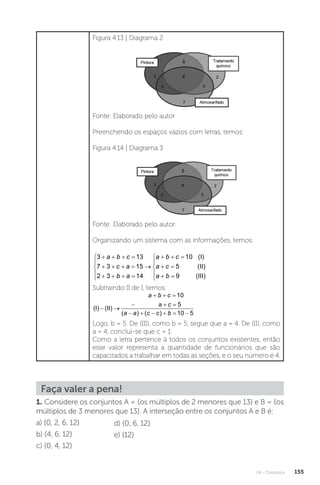
Este documento apresenta um livro sobre raciocínio lógico e matemático. O livro contém quatro unidades, começando com conceitos básicos de matemática, incluindo razão e proporção. A segunda unidade introduz lógica, proposições e argumentação. A terceira unidade trata de dedução e regras de inferência. A quarta e última unidade aborda conjuntos e operações com conjuntos.






































![U1 - Conceitos básicos de matemática
40
De acordo como texto, as quantidades de células produzidas por minuto
e por dia, escritas em potências de base 10, são, respectivamente:
a) 3 . 106
e 432 . 1012
.
b) 3 . 108
e 432 . 1012
.
c) 3 . 106
e 432 . 109
.
d) 3 .106
e 432 . 108
.
e) 3 . 107
e 432 . 109
.
3. Leia o trecho da reportagem intitulada “Brasil avança na produção
mundial de alimentos?”:
“O Brasil se consolidará como uma potência agrícola nos próximos dez
anos e vai disputar a liderança na produção de alimentos com os Estados
Unidos. A projeção é do Ministério da Agricultura, Pecuária e Abastecimento
(Mapa), que, nesta terça-feira, divulgou o estudo Projeções do Agronegócio
2010/11-2020/2021.
[...]
O ministério avalia que o país manterá a dianteira na produção da carne
de frango e carne bovina, e incrementará a produção de carne suína. No
total, o país passará da produção atual de 24,6 milhões de toneladas de
carne para 31,2 milhões de toneladas na temporada 2020/21 (crescimento
de 36,5%)”.
(Fonte: PORTAL BRASIL. Brasil avança na produção mundial de alimentos. 2011. Disponível em:
<http://www.brasil.gov.br/economia-e-emprego/2011/06/brasil-avanca-na-producao-mundial-de-
alimentos>. Acesso em: 9 dez. 2015).
Após ler o texto, podemos dizer que a diferença, em toneladas, entre a
atual produção de carne e a temporada 2020/21 será de:
a) 6,6.106
b) 66.104
c)66.106
d)6,6.105
e)6,6.104](https://image.slidesharecdn.com/livrounico-221102215203-6ceb13ff/85/LIVRO_UNICO-pdf-42-320.jpg)





















![U2 - Introdução à lógica 63
As proposições compostas são formadas por combinações de
duas ou mais proposições simples. Vejamos alguns exemplos:
• P: Carlos é magro e 49 é um quadrado perfeito.
• Q: Carlos é magro e Zélia é avó.
• R: 49 é um quadrado perfeito e Zélia é avó.
Assimile
As proposições simples são representadas por letras minúsculas; já as
proposições compostas são representadas por letras maiúsculas.
Faça você mesmo
1. Leia cada uma das frases a seguir e as classifique em não proposição,
proposição simples ou proposição composta.
I – Você foi ao mercado ontem?
II – Mário é esportista.
III – Vá embora agora!
IV – A água do mar é salgada e a água do rio é doce.
Em lógica, quando trabalhamos com proposições compostas,
fazemos a utilização dos conectivos.
Existem vários tipos de conectivos. Vejamos os mais usuais[RT1]:
• A conjunção e, cujo símbolo é ∧
• A disjunção inclusiva ou, cujo símbolo é ∨
• A disjunção exclusiva ou, cujo símbolo é ∨
• O condicional se ..., então, cujo símbolo é →
• O bicondicional se, e somente se, cujo símbolo é ↔
• A negação não, cujo símbolo é ~
Pesquise mais
A disjunção exclusiva não é muito comum na lógica clássica; seu uso
ocorre em ambientes específicos. Faça uma pesquisa para verificar onde
esse conectivo é mais usado.](https://image.slidesharecdn.com/livrounico-221102215203-6ceb13ff/85/LIVRO_UNICO-pdf-65-320.jpg)