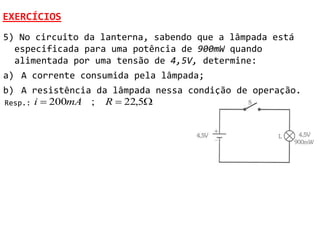
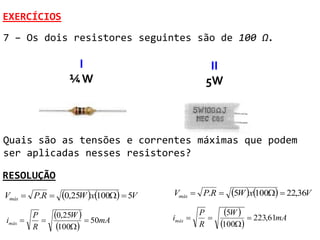
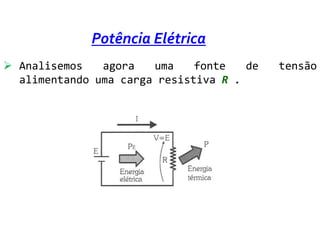
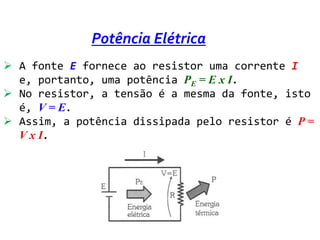
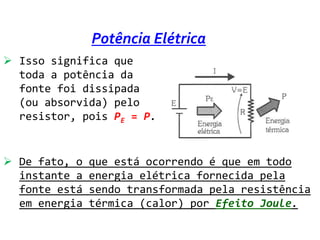
O documento discute conceitos de potência e energia elétrica. Explica que potência é a capacidade de produzir trabalho e é medida em watts. A energia elétrica é a quantidade de trabalho produzido em um intervalo de tempo e é medida em joules. O documento também apresenta exemplos de cálculos de potência e energia em circuitos elétricos e exercícios sobre o tema.

1. Eletricidade e Mecânica
CONTEÚDO:
AULA 6
Potência e Energia Elétrica
OBJETIVO:
Compreender o conceito de potência e energia elétrica
Prof.Dr.Marcos Roberto Bonfadini

2. POTÊNCIA ELÉTRICA
 Os fenômenos elétricos, da mesma forma que os
fenômenos mecânicos ou quaisquer outros tipos de
fenômenos físicos, envolvem sempre transformação ou
conversão de energia de uma forma para outra.
Num dínamo, por exemplo, temos transformação
de energia mecânica em energia elétrica.
Numa lâmpada temos conversão de energia
elétrica em energia térmica e luminosa.

3. POTÊNCIA ELÉTRICA
Capacidade de produzir trabalho
As duas
Fazendo a são
analogia capazes de
com duas realizar
pessoas. trabalho.

4. POTÊNCIA ELÉTRICA
Da mesma maneira as cargas
elétricas possuem uma
capacidade de produzir
trabalho.
A capacidade de produzir
trabalho de uma carga
elétrica é expressa em watt.

5. POTÊNCIA ELÉTRICA
O conceito de potência elétrica P está
associado à quantidade de energia
elétrica  desenvolvida num intervalo
de tempo t por um dispositivo
elétrico.
Matematicamente: J
s

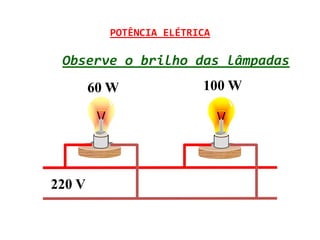
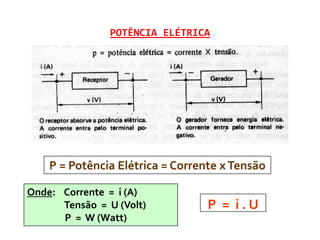
6. POTÊNCIA ELÉTRICA
Mas: Q/t = I
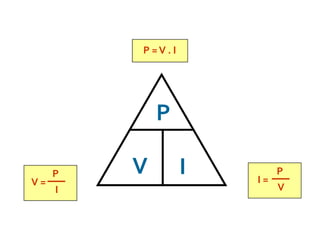
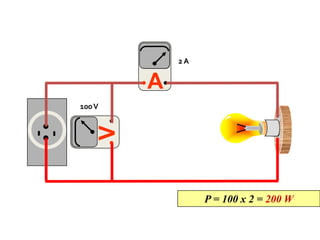
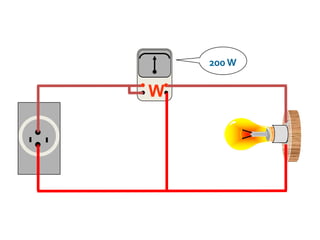
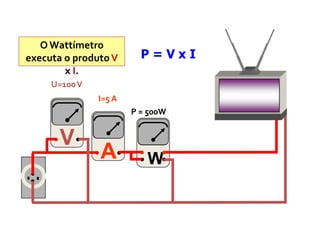
Assim: P = V.I = i.U
 Para unidade de medida de potência
em circuitos CC, em vez de [J/s] ou
[VA], é mais comum a utilização de
uma unidade equivalente denominada
watt [W].

7. POTÊNCIA ELÉTRICA
Unidade de medida da potência elétrica
watt (W)
Símbolo
P (potência)

8. POTÊNCIA ELÉTRICA
Potência da lâmpada
 Capacidade de
produzir trabalho de
100 W
 Se for ligada a uma
fonte de 127 V

9. POTÊNCIA ELÉTRICA
Potência da lâmpada
 Capacidade de
produzir trabalho de
100 W
 Se for ligada a uma
fonte de 220 V

10. POTÊNCIA ELÉTRICA
Observe o brilho das lâmpadas
60 W 100 W
220 V

11. POTÊNCIA ELÉTRICA
P = Potência Elétrica = Corrente x Tensão
Onde: Corrente = i (A)
Tensão = U (Volt) P = i.U
P = W (Watt)

12. Classifique os dispositivos representados abaixo
dizendo se são resistores, geradores ou
receptores.
a) Gerador
b) Receptor
c) Resistor
d) Receptor
e) Gerador

13. P =V . I
P
V=
P V I I=
P
I V

14. 2A
A
100 V
V
P = 100 x 2 = 200 W

15. WATTÍMETRO
 O wattímetro é um instrumento que permite medir a
potência elétrica fornecida ou dissipada por um
elemento.
 O wattímetro implementa o produto das grandezas tensão
e corrente elétrica no elemento, razão pela qual a sua
ligação ao circuito é feita simultaneamente em série e
em paralelo.

16. Constituição do Wattímetro
BOBINA DE CORRENTE
LIGADA EM SÉRIE
BOBINA DE TENSÃO
LIGADA EM PARALELO

17. 200 W
W

18. O Wattímetro
executa o produto V P=VxI
x I.
U=100 V
I=5 A
P = 500W
V
A W

19. EXPRESSÃO DA POTÊNCIA DISSIPADA NUM RESISTOR
(EFEITO JOULE)
 A potência elétrica dissipada num resistor pode ser
calculada pelas seguintes expressões:
P = U. i
 Substituindo: U = Ri, temos:
P = R . i2
 Substituindo: i = U /
R, temos:
P = U2
R

20. Conversões

21. Potência Elétrica
 Analisemos agora uma fonte de tensão
alimentando uma carga resistiva R .

22. Potência Elétrica
 A fonte E fornece ao resistor uma corrente I
e, portanto, uma potência PE = E x I.
 No resistor, a tensão é a mesma da fonte, isto
é, V = E.
 Assim, a potência dissipada pelo resistor é P =
V x I.

23. Potência Elétrica
 Isso significa que
toda a potência da
fonte foi dissipada
(ou absorvida) pelo
resistor, pois PE = P.
 De fato, o que está ocorrendo é que em todo
instante a energia elétrica fornecida pela
fonte está sendo transformada pela resistência
em energia térmica (calor) por Efeito Joule.

24. Potência Elétrica
 No resistor, a potência dissipada em função de R
pode ser calculada pelas expressões:

25. James Watt (1736 -1819)
 Escocês, aprendiz de
fabricante de ferramentas,
logo cedo interessou-se pelas
descobertas no campo da
eletricidade.
 Quando se tornou fabricante de peças e de
instrumentos de matemática na Universidade de
Glasgow, Watt criou uma máquina a vapor muito
mais rápida e econômica, permitindo a
mecanização das indústrias em grande escala.
 A unidade de medida de potência elétrica é
watt, em sua homenagem.

26. Conceito de Energia Elétrica
 Inicialmente, vimos que P = /t. Assim, a energia
elétrica desenvolvida em um circuito pode ser
calculada pela fórmula:
 = P . t
 Por esta expressão, a unidade de medida de energia
elétrica é joule [J] ou watt.segundo [Ws].

27. Conceito de Energia Elétrica
 No quadro de distribuição de energia elétrica
de uma residência, prédio ou indústria, existe
um medidor de energia que indica constantemente
a quantidade de energia que está sendo
consumida.
 Mensalmente, a empresa
concessionária faz a leitura da
energia elétrica
consumida, calculando a tarifa
correspondente a ser paga pelo
usuário.

28. Conceito de Energia Elétrica
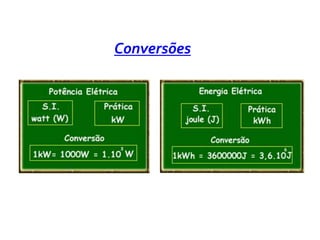
 Como a ordem de grandeza do consumo de energia
elétrica em residências e indústrias é muito
elevada, a unidade de medida utilizada, no lugar
de [Ws], é o quilowatt. hora [kWh].
 No caso da quantidade
de energia elétrica
produzida por uma
usina hidrelétrica,
termoelétrica ou
nuclear, a unidade de
medida utilizada é
megawatt.hora [MWh].

29. Fusível e Disjuntor
 Os equipamentos eletrônicos e as instalações
elétricas residenciais e industriais possuem
fusíveis ou disjuntores de proteção contra
sobrecarga de corrente.
 Eles são dimensionados pela corrente elétrica
máxima que suportam.

30. Fusível e Disjuntor
 O fusível possui um filamento à base de estanho
(baixo ponto de fusão) que se derrete quando a
corrente que passa por ele é maior que a sua
corrente nominal.
 Quando isso ocorre, é preciso trocá-lo por outro
após a correção do problema que causou a sua
queima.
Vidro Cartucho

31. Fusível e Disjuntor
 No disjuntor, quando a corrente é maior que a sua
corrente nominal, ele apenas se desarma.
 Após a correção do problema que causou o seu
desarme, basta rearmá-lo para que a instalação
elétrica volte a ser energizada.

32. EXERCÍCIOS
1- A corrente através de um condutor de cobre cuja
resistência é de 2,5 ohms, tem 45 ampères de
intensidade. Qual a potência dissipada ao longo do
condutor, sob forma de calor Joule?
Resp.: P  5062,5W i = 45 A
Cobre
R = 2,5 Ω
P=?

33. EXERCÍCIOS
1- A corrente através de um condutor de cobre cuja
resistência é de 2,5 ohms, tem 45 ampères de
intensidade. Qual a potência dissipada ao longo do
condutor, sob forma de calor Joule?
Resp.: P  5062,5W i = 45 A
RESOLUÇÃO
Cobre
P  R.i 2  2,5 45 A  5062 ,5W
2
. R = 2,5 Ω
P=?
P = 5062,5 W

34. EXERCÍCIOS
2- Um aquecedor elétrico de água é constituído por um
fio condutor de 5 ohms que deve ser ligado em 120
volts. Qual a potência consumida pelo aquecedor?
Resp.: P  2880W
R=5Ω 120 V
P=?

35. EXERCÍCIOS
2- Um aquecedor elétrico de água é constituído por um
fio condutor de 5 ohms que deve ser ligado em 120
volts. Qual a potência consumida pelo aquecedor?
RESOLUÇÃO Resp.: P  2880W
U 2 120 2 R=5Ω 120 V
P   2880 W
R 5
P=?
P = 2880 W

36. EXERCÍCIOS
3-Qual é a corrente elétrica consumida no exercício
anterior? Resp.: i  24 A
R=5Ω 120 V

37. EXERCÍCIOS
3-Qual é a corrente elétrica consumida no exercício
anterior? Resp.: i  24 A
R=5Ω 120 V
RESOLUÇÃO
U
U  R.i  i 
R
U 120 V 
i   24 A
R 5 
i  24 A

38. EXERCÍCIOS
4-Calcule a corrente elétrica consumida no exercício
02 se o aquecedor elétrico for ligado em uma tensão
elétrica de 220V? Resp.: i  13,09 A
220 V
P= 2880 W

39. EXERCÍCIOS
4-Calcule a corrente elétrica consumida no exercício
02 se o aquecedor elétrico for ligado em uma tensão
elétrica de 220V? Resp.: i  13,09 A
RESOLUÇÃO
P
P  U .i  i  220 V
U
P 2880 W 
i   13,09 A
U 220V 
P= 2880 W
i  13,09 A

40. EXERCÍCIOS
5) No circuito da lanterna, sabendo que a lâmpada está
especificada para uma potência de 900mW quando
alimentada por uma tensão de 4,5V, determine:
a) A corrente consumida pela lâmpada;
b) A resistência da lâmpada nessa condição de operação.
Resp.: i  200mA ; R  22,5

41. EXERCÍCIOS
5) No circuito da lanterna, sabendo que a lâmpada está
especificada para uma potência de 900mW quando
alimentada por uma tensão de 4,5V, determine:
a) A corrente consumida pela lâmpada;
b) A resistência da lâmpada nessa condição de operação.
Resp.: i  200mA ; R  22,5
RESOLUÇÃO
P
P  U .i  i 
U

P 900 x10 3W
i 

 0,2 A  200 mA
U 4,5V 
i  200mA

42. EXERCÍCIOS
5) No circuito da lanterna, sabendo que a lâmpada está
especificada para uma potência de 900mW quando
alimentada por uma tensão de 4,5V, determine:
a) A corrente consumida pela lâmpada;
b) A resistência da lâmpada nessa condição de operação.
Resp.: i  200mA ; R  22,5
RESOLUÇÃO
U2 U2
P  R
R P
R
U 2

4,5V   22,5
2
P 
900x103W 
R  22,5

43. EXERCÍCIOS
6 – Considere um resistor com as seguintes
especificações: 1 KΩ - 1/2 W.
a) Qual é a corrente Imáx e a tensão Vmáx, que ele
pode suportar? imáx  22 ,36 mA U  22,36V
b) Que potência P' ele dissiparia caso a tensão
aplicada V' fosse metade de Vmáx? P  125mW
c) Quanto vale a relação Pmáx/P' e qual conclusão
pode ser tirada? P  Pmáx
4

44. EXERCÍCIOS
6 – Considere um resistor com as seguintes
especificações: 1 KΩ - 1/2 W.
a) Qual é a corrente Imáx e a tensão Vmáx, que ele
pode suportar? imáx  22 ,36 mA U  22,36V
b) Que potência P' ele dissiparia caso a tensão
aplicada V' fosse metade de Vmáx? P  125mW
c) Quanto vale a relação Pmáx/P' e qual conclusão
pode ser tirada? P  Pmáx
4
RESOLUÇÃO U2
P P  U  R.P
P  R.i 2
 i R
R
U  R.P  10000,5W   22,36V
.
imáx 
P

0,5W   22,36mA
R 1x10 
3
imáx  22 ,36 mA U  22,36V

45. EXERCÍCIOS
6 – Considere um resistor com as seguintes
especificações: 1 KΩ - 1/2 W.
a) Qual é a corrente Imáx e a tensão Vmáx, que ele
pode suportar? imáx  22 ,36 mA U  22,36V
b) Que potência P' ele dissiparia caso a tensão
aplicada V' fosse metade de Vmáx? P  125mW
c) Quanto vale a relação Pmáx/P' e qual conclusão
pode ser tirada? P  Pmáx
4
RESOLUÇÃO
U 2 U máx 22,36V 
P  U    11,18V
R 2 2
P 
U2

11,18V   125mW
2
R 1000 P  125mW

46. EXERCÍCIOS
6 – Considere um resistor com as seguintes
especificações: 1 KΩ - 1/2 W.
a) Qual é a corrente Imáx e a tensão Vmáx, que ele
pode suportar? imáx  22 ,36 mA U  22,36V
b) Que potência P' ele dissiparia caso a tensão
aplicada V' fosse metade de Vmáx? P  125mW
c) Quanto vale a relação Pmáx/P' e qual conclusão
pode ser tirada? P  Pmáx
4
RESOLUÇÃO
Pmáx

0,5W   4 A potência dissipada divide-se por quatro
P 125 mW  quando a tensão aplicada divide-se por dois

47. EXERCÍCIOS
7 – Os dois resistores seguintes são de 100 Ω.
I II
¼W 5W
Quais são as tensões e correntes máximas que podem
ser aplicadas nesses resistores?

48. EXERCÍCIOS
7 – Os dois resistores seguintes são de 100 Ω.
I II
¼W 5W
Quais são as tensões e correntes máximas que podem
ser aplicadas nesses resistores?
RESOLUÇÃO
Vmáx  P.R  0,25W x100  5V Vmáx  P.R  5W x100  22,36V
P 0,25W   50mA imáx 
P

5W   223,61mA
imáx   100
R 100 R

49. EXERCÍCIOS
8 – Uma lâmpada residencial está especificada para 127V /
100W. Determine:
a) A energia elétrica consumida por essa lâmpada num
período de cinco horas diárias num mês de 30 dias.
b) O valor a ser pago por esse consumo, sabendo que a
empresa de energia elétrica cobra a tarifa de R$ 0,30
por kWh mais um imposto de 33,33%.
Resp.: E  15kWh R$  6,00

50. EXERCÍCIOS
8 – Uma lâmpada residencial está especificada para 127V /
100W. Determine:
a) A energia elétrica consumida por essa lâmpada num
período de cinco horas diárias num mês de 30 dias.
b) O valor a ser pago por esse consumo, sabendo que a
empresa de energia elétrica cobra a tarifa de R$ 0,30
por kWh mais um imposto de 33,33%.
Resp.: E  15kWh R$  6,00
RESOLUÇÃO
E  P.t  100Wx 5hx30 dias  15 kWh E  15kWh
R$  E x tarifa   Txa imposto 
 15 kWhx0,30 x1,3333   6,00 R$  6,00

51. EXERCÍCIOS
9 – Uma turbina de uma usina hidrelétrica com
capacidade de 100000 kWh abastece uma região com
tensão de 127V. Quantas lâmpadas de 200W/127V essa
turbina pode alimentar simultaneamente?
Resp.: N
o
Lâmp .  500000 lâmpadas

52. EXERCÍCIOS
9 – Uma turbina de uma usina hidrelétrica com
capacidade de 100000 kWh abastece uma região com
tensão de 127V. Quantas lâmpadas de 200W/127V essa
turbina pode alimentar simultaneamente?
RESOLUÇÃO Resp.: N
o
Lâmp .  500000 lâmpadas
E 100000 kWh 
N o
   500000 lâmpadas
200Wh 
Lâmp .
P

53. • Obrigado!
• E até a próxima aula...