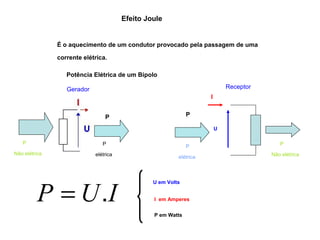
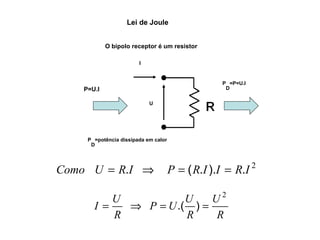
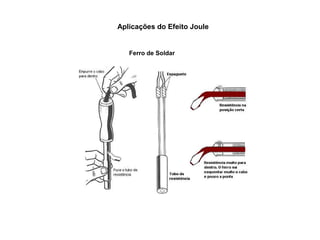
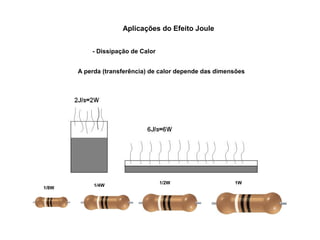
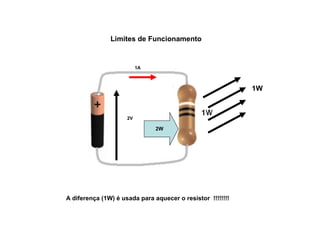
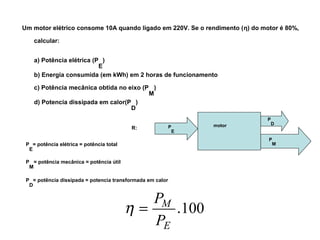
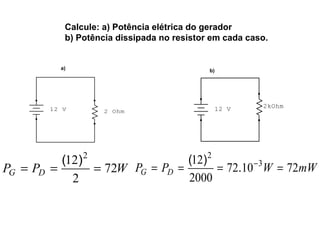
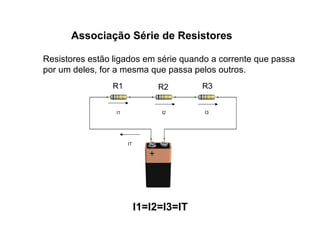
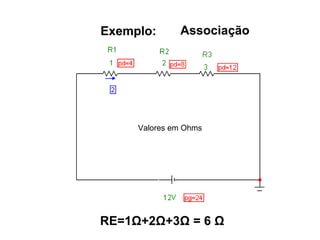
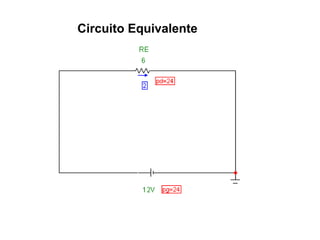
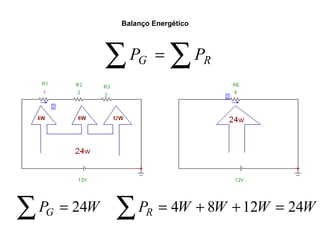
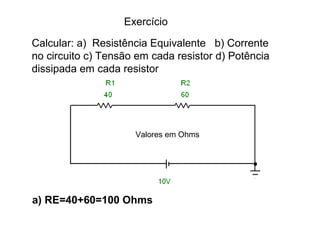
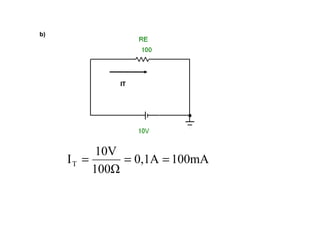
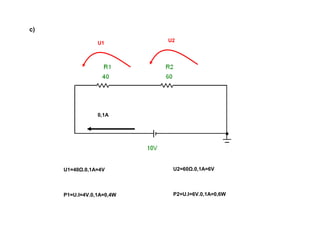
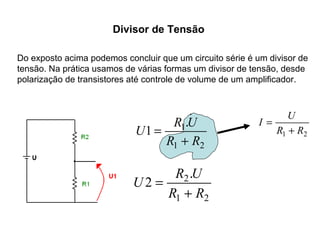
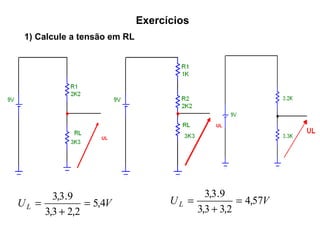
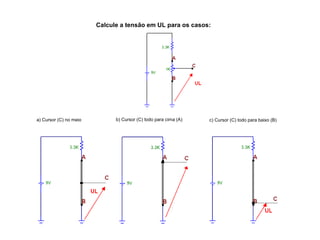
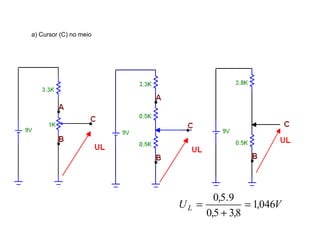
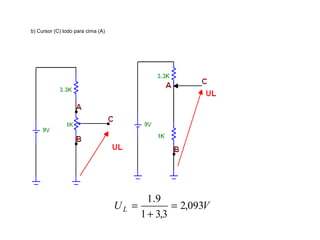
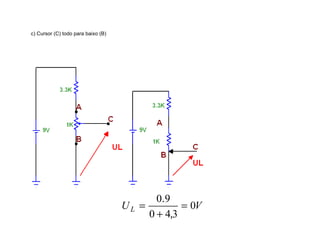
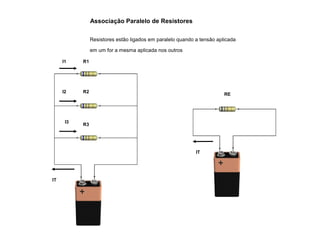
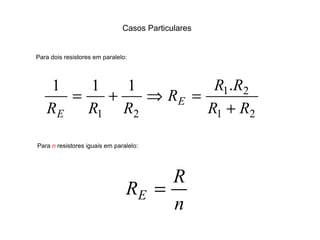
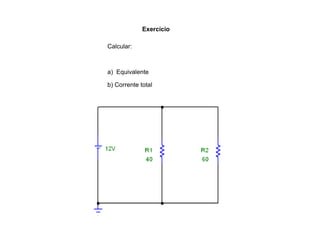
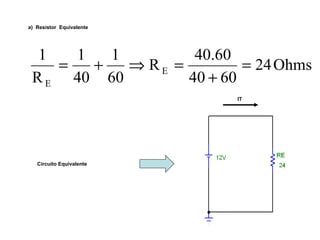
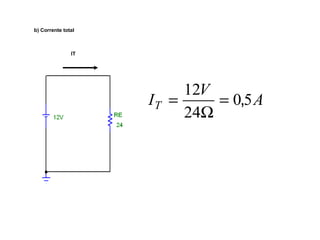
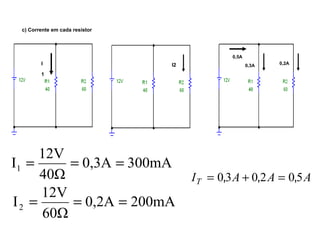
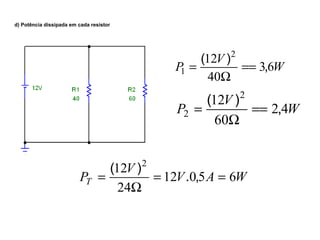
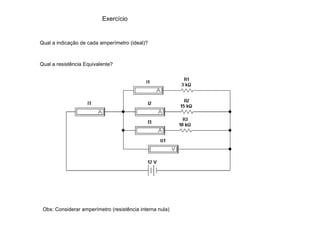
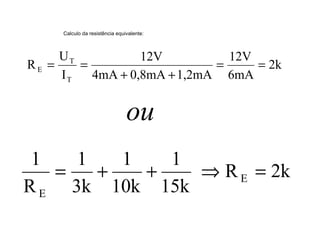
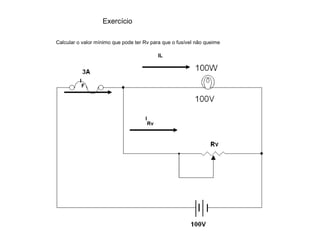
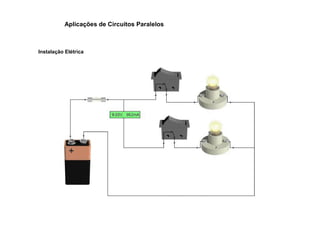
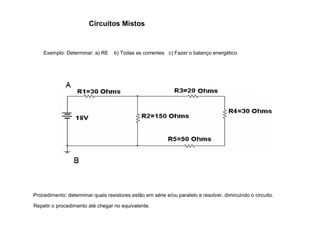
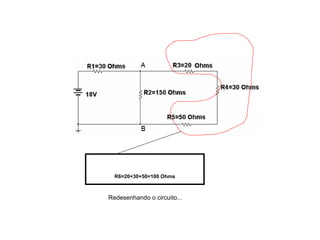
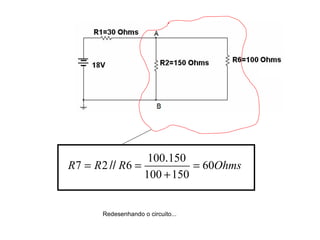
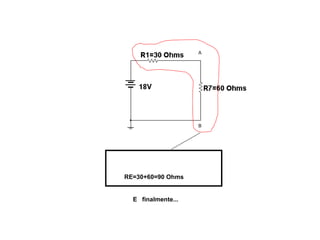
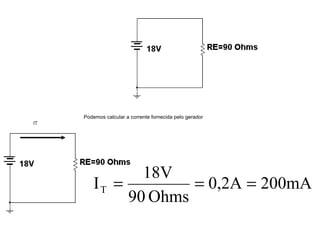
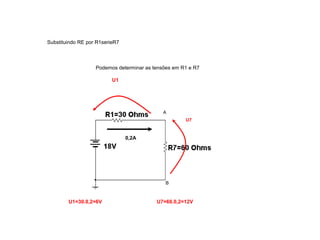
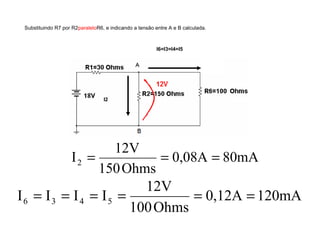
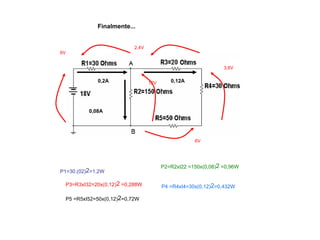
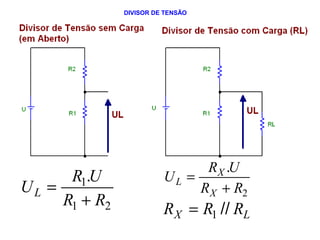
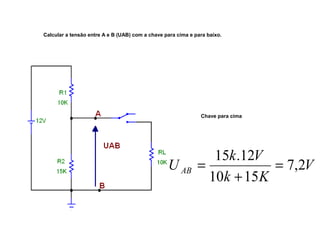
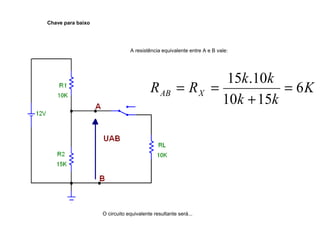
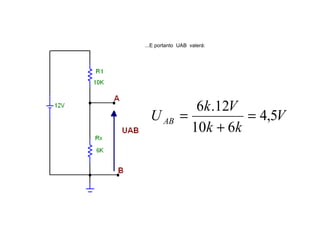
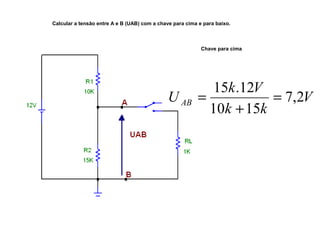
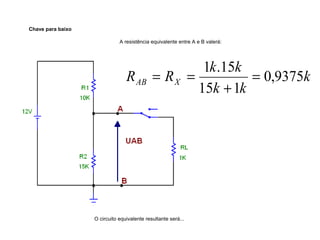
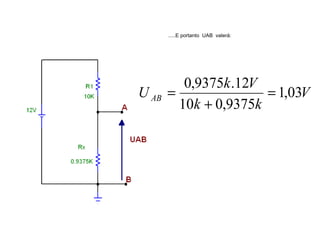
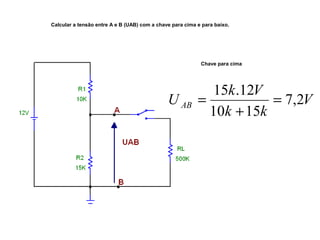
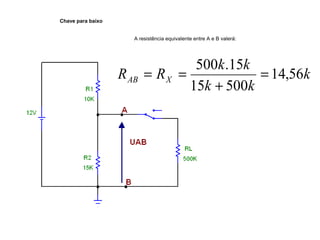
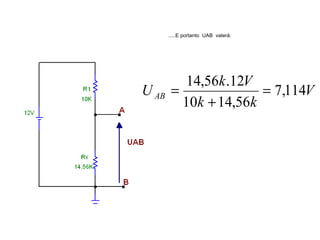
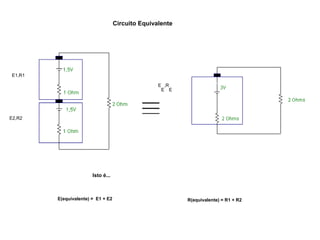
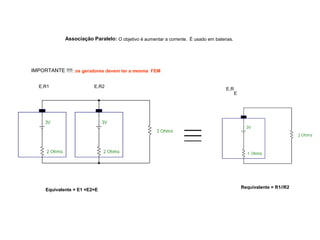
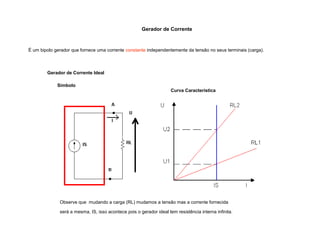
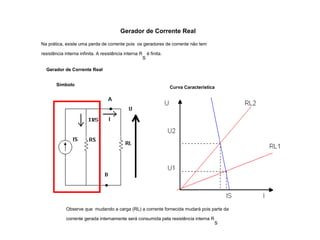
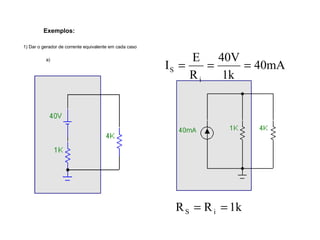
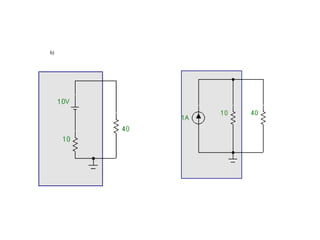
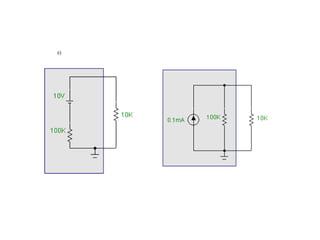
O documento aborda conceitos de eletrônica digital, focando em potência e energia, incluindo definições de trabalho e energia em joules, caloria e kWh. Ele explica a relação entre potência e trabalho, apresenta exemplos práticos de cálculo de potência e energia e discute o efeito Joule em diversos dispositivos elétricos. O texto também abrange a associação de resistores, seus tipos e aplicações em circuitos elétricos, além de exercícios para aplicar os conceitos aprendidos.

1. Curso de Eletrônica
Foco em Eletrônica digital para
uso da Plataforma Arduino

2. Conceito de Potência e Energia
“Trabalho e energia em física são sinônimos. Toda vez que um trabalho é realizado
uma certa quantidade de energia é transformada e uma força estará atuando em
algum corpo”
Unidades de Trabalho (Energia)
Joule(J) é a unidade oficial de energia e trabalho
Outras Unidades
Caloria (cal)=4,18J
kWh=3,6x106J

3. Unidades de Potência
Potência e trabalho (energia transformada) estão relacionadas por:
P = t t = P.t ou
t
onde τ(tau) é o trabalhorealizado(emJoules)
t é otempo gasto para realizar otrabalho(emsegundos)
Pé a potência desenvolvida (emwatts)
Outra Unidade: HP 1HP = 746W
OBS: A letra W, em alguns livros, é usada para representar trabalho (work em inglês) não é usada para não
confundir com W de Watt

4. Exemplo
Imagine você deslocando um saco de açúcar de 5Kg de uma altura
de 1m em 1s.
Você gastou energia? Realizou um trabalho? Desenvolveu uma potência?
Qual foi a quantidade de energia gasta? Do que depende essa
Energia ?
De acordo com a Física.......................

5. DE = M.g.Dh (em Joules)
M massa do corpo em Kg
g aceleração da gravidade(@ 9,8m/ s2 )
Dh deslocamento (em m)
DE = 5.9,8.1 = 49J

6. Qual a potencia desenvolvida?
P = t
P J 49 49
= 49 = / =
J s W
s
1
t
É a potência desenvolvida ao deslocar o saco de 5kg de açúcar de 1m .

7. Mais um exemplo...
Qual a quantidade de energia consumida num banho de 30min,
se o chuveiro tem uma potência de 5000W (5kW)?
Dados: P=5000W=5000J/s=5kW t=30min=1800s=0,5h
t = P.t = 5000.1800 = 9.000.000J
ou em KWh
t = P.t = 5kW.0,5h = 2,5kWh

8. Efeito Joule
É o aquecimento de um condutor provocado pela passagem de uma
corrente elétrica.
Potência Elétrica de um Bipolo
Gerador Receptor
P
P = U.I U em Volts
I em Amperes
P em Watts
U
I
P
P
Não elétrica
P
elétrica
P
elétrica
P
Não elétrica

9. Exemplo
Qual é a potência desenvolvida (em HP e W) por uma pessoa para
elevar um corpo de 5kg a uma altura de 1,5m em 1s? Adotar g=10m/s2
R:
t = DEP = 5.10.1,5 = 75J como t = 1s
= t = 75 = / =
P 75 75
J s W
J
s
t
1
1HP = 746W ® P @ 0,1HP

10. Lei de Joule
O bipolo receptor é um resistor
I
U
P=U.I
P
D
=P=U.I
Como U = R.I Þ P = (R.I ).I = R.I 2
U
R
P U U
R
I U
R
2
= Þ = .( ) =
P
D
=potência dissipada em calor

11. Aplicações do Efeito Joule
- Chuveiro, aquecedores, forno elétrico, lâmpada, Ferro de soldar, etc.
Resistência de Chuveiro Lâmpada

12. Aplicações do Efeito Joule
Ferro de Soldar

13. Aplicações do Efeito Joule
- Proteção de Circuitos
Fusíveis Disjuntores

14. Aplicações do Efeito Joule
- Dissipação de Calor
A perda (transferência) de calor depende das dimensões
1/8W 1/4W 1/2W 1W

15. Calor em Excesso
Dissipadores de Calor: Placa metálica ligada ao componente.

16. Limites de Funcionamento
2V
1A
1W
2W
A diferença (1W) é usada para aquecer o resistor !!!!!!!!

17. Exercícios
As especificações de um resistor são: 1kOhm/1W. Calcule qual a
máxima tensão que pode ser aplicada ao resistor.
R: R=1kOhm=1000 Ohm P=1W
0,0316A 31,6mA
P R.I I 1 Máx
1000
2
Máx Máx = ® = = =
U R.I 1k.31,6mA 31,6V Máx Máx = = =

18. Um motor elétrico consome 10A quando ligado em 220V. Se o rendimento (η) do motor é 80%,
calcular:
a) Potência elétrica (P
E
)
b) Energia consumida (em kWh) em 2 horas de funcionamento
c) Potência mecânica obtida no eixo (P
M
)
d) Potencia dissipada em calor(P
D
)
R: P motor
E
P
D
P
P = potência elétrica = potência total
M
E
P
M
= potência mecânica = potência útil
P
D
= potência dissipada = potencia transformada em calor
M
P
.100
E
h = P

19. P
E
= P
M
+ P
D
→ conservação da energia
R:
a)
P U.I 220.10A 2200W 2,2KW E = = = =
b) τ = P.t = 2,2kW.2h = 4,4kWh
c)
= M Þ = =
η M
P 0,8.2200 1760W
P
P
E
d) PD= PE - PM = 2200 -1760 = 440W

20. Um fio de resistência 5 Ohms é imerso em uma massa de água
de 1kg a 20oC. O conjunto está dentro de um calorímetro ideal.
O fio é ligado a uma tensão de 100V. Calcule que temperatura
a massa de água atingirá após 1min.
obs : da física Q = m.c.Δq
Q= quantidade de calor em calorias (cal)
m= massa de água (em g)
Δθ= variação de temperatura=θF-θi (em ºC)
c= calor especifico da água (em cal/g. ºCC)) cc==11cal/gºC
100 2
= = =
R: P W J / s ( ) 2000 2000
5

21. Para t=1min=60s a quantidade de energia fornecida à água será
de:
t = P.t = 2000.60 = 120.000J
= 120.000 = .
Em calorias: Q 30 000cal
4
como Q = m.c.Dq
C
.
Q 30o
D = = 30 000 =
m c
.
1000 1
.
q
oC
Dq =q F - 20 = 30 Þq F = 50

22. Calcule: a) Potência elétrica do gerador
b) Potência dissipada no resistor em cada caso.
a)
12 V 2 Ohm
b)
12 V 2kOhm
12 2
2
= = ( ) = . - =
= = ( ) = PG PD 72 10 W 72mW
PG PD 72W
2
12 3
2000

23. Associação de Resistores
Resistores são associados para:
•Obter outro valor de resistência.
•Dividir uma tensão.
•Dividir uma corrente
Tipos de Associação de Resistores:
Associação em Serie
Associação em Paralelo
Associação Mista
Associação em Estrela
Associação em Triângulo

24. Associação Série de Resistores
Resistores estão ligados em série quando a corrente que passa
por um deles, for a mesma que passa pelos outros.
R1 R2 R3
I1 I2 I3
IT
I1=I2=I3=IT

25. Por outro lado a tensão total aplicada na associação será dividida
entre os resistores da associação de forma que:
U
T
= U
+U
2
1
+U
3

26. Resistor Equivalente (RE)
É um único resistor que pode substituir a associação e o
resto do circuito não nota nenhuma diferença. Para isso o
seu valor deve ser dado por:
RE=R1+R2+.....+Rn
E...
PE=P1+P2+.....+Pn
OBS: O equivalente será sempre MAIOR do que o
maior dos resistores da associação.

27. Exemplo: Associação
Valores em Ohms
RE=1Ω+2Ω+3Ω = 6 Ω

28. Circuito Equivalente

29. Balanço Energético
åPG = åPR
åPG = 24W åPR = 4W + 8W +12W = 24W

30. Exercício
Calcular: a) Resistência Equivalente b) Corrente
no circuito c) Tensão em cada resistor d) Potência
dissipada em cada resistor
Valores em Ohms
a) RE=40+60=100 Ohms

31. b)
IT
I 10V T = = =
0,1A 100mA
100Ω

32. c)
U1 U2
0,1A
U1=40Ω.0,1A=4V U2=60Ω.0,1A=6V
P1=U.I=4V.0,1A=0,4W P2=U.I=6V.0,1A=0,6W

33. Divisor de Tensão
Do exposto acima podemos concluir que um circuito série é um divisor de
tensão. Na prática usamos de várias formas um divisor de tensão, desde
polarização de transistores até controle de volume de um amplificador.
= .
U 1 R 1
U
R +
R
1 2
= .
U 2 R 2
U
R +
R
1 2
I U
R1 +
R2
=

34. Exercícios
1) Calcule a tensão em RL
, . =
+
33 9 ,
, ,
UL 5 4V
33 2 2
=
UL
UL
, . =
+
33 9 ,
, ,
UL 4 57V
33 3 2
=

35. Calcule a tensão em UL para os casos:
a) Cursor (C) no meio b) Cursor (C) todo para cima (A) c) Cursor (C) todo para baixo (B)

36. a) Cursor (C) no meio
, . =
+
0 5 9 ,
, ,
UL 1046V
0 5 38
=

37. b) Cursor (C) todo para cima (A)
. =
+
1 9 ,
,
UL 2 093V
1 33
=

38. c) Cursor (C) todo para baixo (B)
0 9 =
+
UL 0V
0 4 3
=
,
.

39. Associação Paralelo de Resistores
Resistores estão ligados em paralelo quando a tensão aplicada
em um for a mesma aplicada nos outros
R1
R2
R3
IT
I1
I2
I3
IT
RE

40. Características
IT = I1 + I2 + I3
UT =U1 =U2 = U3
1 = 1 + 1 + 1 ou G E
= G + G +
G
R E
R R R 1 2 3
1 2 3
PT = P1 + P2 + P3
OBS: O equivalente será sempre MENOR que o menor dos resistores da associação

41. Casos Particulares
Para dois resistores em paralelo:
= + Þ = .
R R R
1 2
R R R E
E +
1 2
1 1 1
1 2
R R
Para n resistores iguais em paralelo:
R R E =
n

42. Exercício
Calcular:
a) Equivalente
b) Corrente total
c) Corrente em cada resistor
d) Potência dissipada em cada resistor

43. a) Resistor Equivalente
24Ohms
R 40.60
40 60
1
60
1
40
1
R
E
E
=
+
= + Þ =
Circuito Equivalente
IT

44. b) Corrente total
IT V 0 5A
12 = ,
W
24
=
IT

45. c) Corrente em cada resistor
I
1
I 12V 1 = = =
0,3A 300mA
40Ω
I2
IT = 0,3A + 0,2A = 0,5A
I 12V 2 = = =
0,2A 200mA
60Ω
0,5A
0,3A 0,2A

46. d) Potência dissipada em cada resistor
12 2
1 , ( ) ==
P V 3 6W
W
40
=
12 2
2 , ( ) ==
P V 2 4W
W
60
=
12 2
= ( ) . ,
PT V 12V 0 5A 6W
24
= =
W

47. Exercício
Qual a indicação de cada amperímetro (ideal)?
Qual a resistência Equivalente?
Obs: Considerar amperímetro (resistência interna nula)

48. Podemos determinar cada uma das correntes por:
4mA
I 12V 1 = =
3k
0,8mA
I 12V 2 = =
15k
1,2mA
I 12V 3 = =
10k

49. Calculo da resistência equivalente:
2k
12V
E = =
6mA
12V
4mA 0,8mA 1,2mA
U
I
R
T
T
+ +
= =
ou
R 2k
1
15k
1
10k
1
3k
1
R
E
E
= + + Þ =

50. Exercício
Calcular o valor mínimo que pode ter Rv para que o fusível não queime
I
Rv
IL
I
F

51. Aplicações de Circuitos Paralelos
Instalação Elétrica

52. Circuitos Mistos
Exemplo: Determinar: a) RE b) Todas as correntes c) Fazer o balanço energético
Procedimento: determinar quais resistores estão em série e/ou paralelo e resolver, diminuindo o circuito.
Repetir o procedimento até chegar no equivalente.

53. R6=20+30+50=100 Ohms
Redesenhando o circuito...

54. = // = .
7 2 6 100 150 =
R R R 60Ohms
+
100 150
Redesenhando o circuito...

55. RE=30+60=90 Ohms
E finalmente...
A
B

56. IT
Podemos calcular a corrente fornecida pelo gerador
I 18V T = = =
0,2A 200mA
90 Ohms

57. Substituindo RE por R1serieR7
Podemos determinar as tensões em R1 e R7
0,2A
A
B
U1
U7
U1=30.0,2=6V U7=60.0,2=12V

58. Substituindo R7 por R2paraleloR6, e indicando a tensão entre A e B calculada.
I2
I6=I3=I4=I5
I 12V 2 = = =
0,08A 80mA
150Ohms
I I I I 12V 6 3 4 5 = = = = = =
0,12A 120mA
100Ohms

59. Finalmente...
0,2A
0,08A
0,12A
6V
P1=30.(02)2=1,2W
3,6V
6V
P2=R2xI22 =150x(0,08)2 =0,96W
12V
2,4V
P3=R3xI32=20x(0,12)2 =0,288W P4 =R4xI4=30x(0,12)2=0,432W
P5 =R5xI52=50x(0,12)2=0,72W

60. Balanço Energético
PG PR
PG1 18.0,2=3,6W PR1 1,200W
PR2 0,960W
PR3 0,288W
PR4 0,432W
PR5 0,720W
PGT 3,6W PRT 3,6W

61. = .
U R U L +
1
R R
1 2
DIVISOR DE TENSÃO
U = R X
.
U
L R X
+
R2
RX = R1 // RL

62. Calcular a tensão entre A e B (UAB) com a chave para cima e para baixo.
Chave para cima
U k V AB 7,2
V
15 .12 =
k +
K
10 15
=

63. Chave para baixo
A resistência equivalente entre A e B vale:
R R k k AB X 6
O circuito equivalente resultante será...
K
15 .10 =
k +
k
10 15
= =

64. ...E portanto UAB valerá:
U k V AB 4,5
V
6 .12 =
k +
k
10 6
=

65. Calcular a tensão entre A e B (UAB) com a chave para cima e para baixo.
Chave para cima
U k V AB 7,2
V
15 .12 =
k +
k
10 15
=

66. Chave para baixo
A resistência equivalente entre A e B valerá:
R R k k AB X 0,9375
O circuito equivalente resultante será...
k
1 .15 =
k +
k
15 1
= =

67. .....E portanto UAB valerá:
U k V AB 1,03
V
0,9375 .12 =
k +
k
10 0,9375
=

68. Calcular a tensão entre A e B (UAB) com a chave para cima e para baixo.
Chave para cima
U k V AB 7,2
V
15 .12 =
k +
k
10 15
=

69. Chave para baixo
k
A resistência equivalente entre A e B valerá:
R R k k AB X 14,56
500 .15 =
+
k k
15 500
= =

70. .....E portanto UAB valerá:
U k V AB 7,114
V
14,56 .12 =
k +
k
10 14,56
=

71. Associação de Geradores de Tensão Real
Associação Série: O principal objetivo é aumentar a tensão, é o caso mais comum.

72. Circuito Equivalente
Isto é...
E(equivalente) = E1 + E2 R(equivalente) = R1 + R2
E1,R1
E2,R2
E
E
,R
E

73. Associação Paralelo: O objetivo é aumentar a corrente. É usado em baterias.
IMPORTANTE !!!!: os geradores devem ter a mesma FEM
E,R1 E,R2 E,R
E
Equivalente = E1 =E2=E Requivalente = R1//R2

74. Associação Mista: É usada quando é necessário aumenta tensão e corrente.
Aplicação: Bateria do carro, Painel solar
+
-

75. Gerador de Corrente
É um bipolo gerador que fornece uma corrente constante independentemente da tensão no seus terminais (carga).
Gerador de Corrente Ideal
Símbolo
Curva Característica
Observe que mudando a carga (RL) mudamos a tensão mas a corrente fornecida
será a mesma, IS, isso acontece pois o gerador ideal tem resistência interna infinita.

76. Gerador de Corrente Real
Na prática, existe uma perda de corrente pois os geradores de corrente não tem
resistência interna infinita. A resistência interna R
S
é finita.
Gerador de Corrente Real
Símbolo Curva Característica
Observe que mudando a carga (RL) a corrente fornecida mudará pois parte da
corrente gerada internamente será consumida pela resistência interna R
S

77. Equivalência entre um Gerador de Tensão e um Gerador de Corrente
Dado um gerador de tensão existe um gerador de corrente que lhe é equivalente, isto é,
do ponto de vista de uma carga tanto faz ela estar ligada no gerador de tensão ou no de corrente.
Para haver equivalência entre o gerador de corrente (IS, RS) e o
gerador de tensão (E, Ri ) deve haver a seguinte relação:

78. Dada a fonte de corrente para obter a fonte de tensão equivalente:
Dada a fonte de tensão para obter a fonte de corrente equivalente:

79. Exemplos:
1) Dar o gerador de corrente equivalente em cada caso
40V
I E
a) 40mA
S = = =
1k
R
i
R R 1k S i = =

80. b)

81. c)

82. Referência:
http://www.eletronica24h.com.br