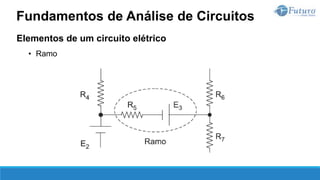
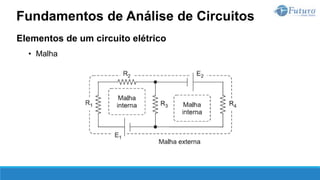
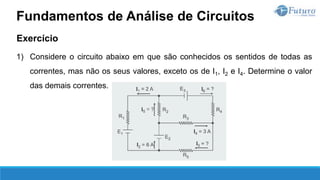
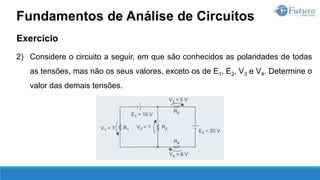
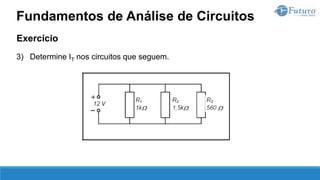
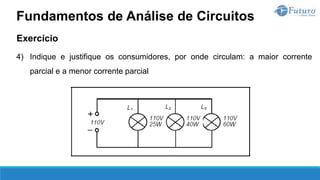
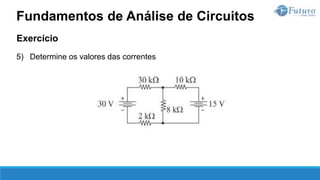
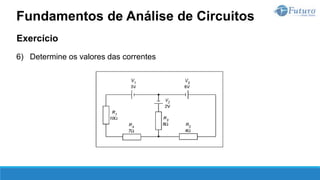
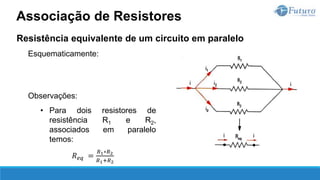
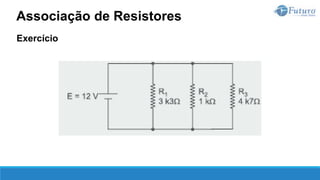
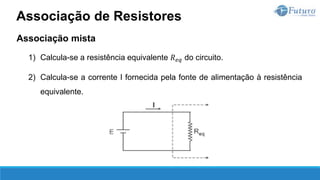
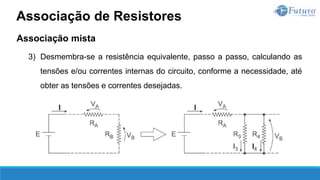
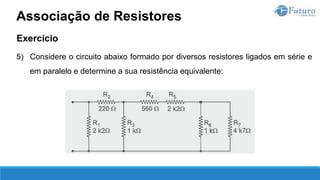
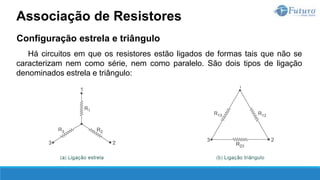
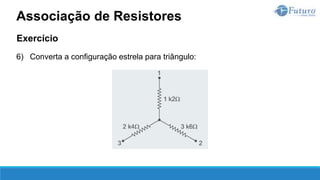
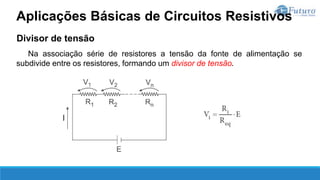
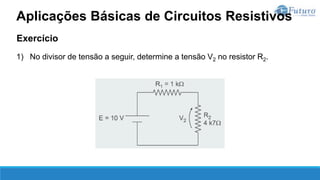
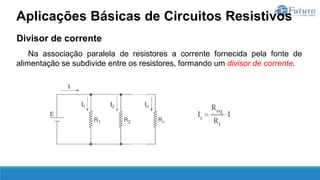
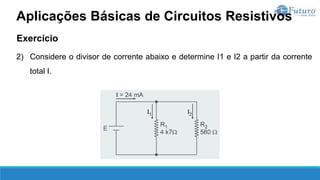
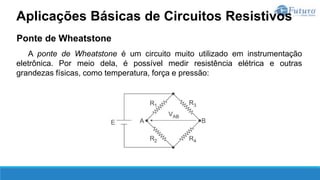
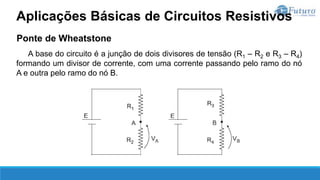
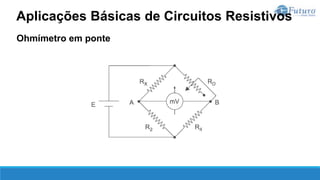
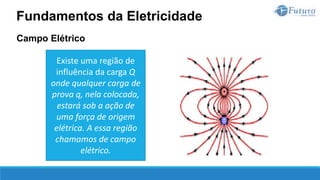
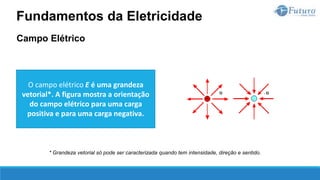
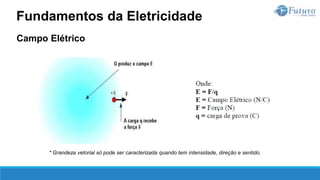
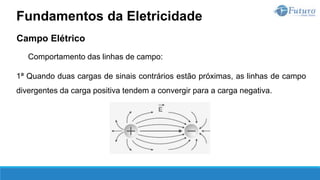
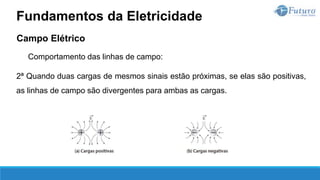
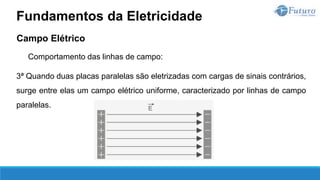
O documento apresenta o conteúdo programático de uma disciplina de eletricidade básica, dividido em 9 capítulos que abordam conceitos matemáticos, fundamentos de eletricidade, tensão e corrente elétrica, equipamentos de bancada, resistência elétrica, potência e energia elétricas, fundamentos de análise de circuitos e aplicações básicas de circuitos resistivos.














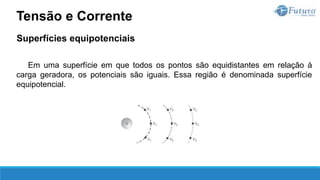

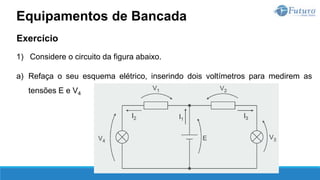
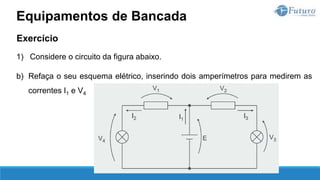
![Tensão elétrica
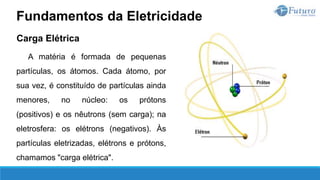
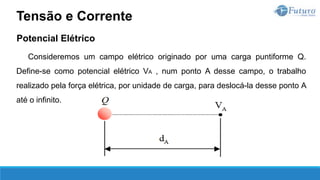
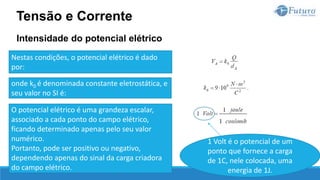
A diferença de potencial elétrico entre dois pontos A e B é denominada tensão
elétrica, cuja unidade de medida é o volt [V].
Tensão e Corrente](https://image.slidesharecdn.com/eletricidadebsica-230619042553-dfc05ef2/85/Eletricidade-Basica-pptx-32-320.jpg)
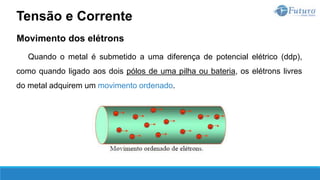
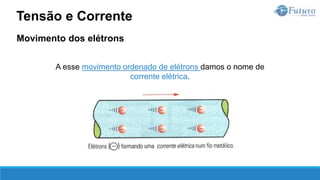
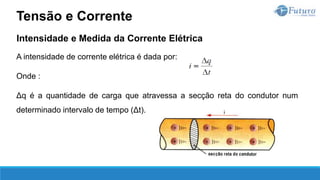


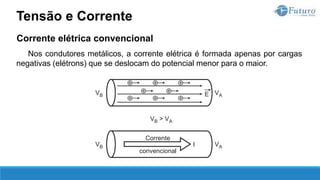


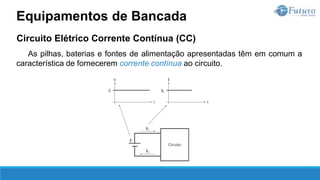
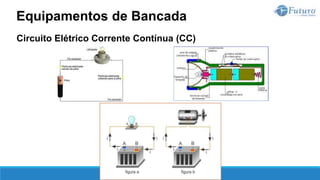
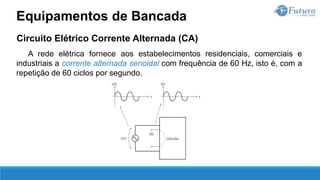


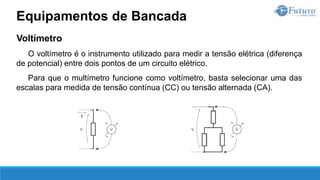














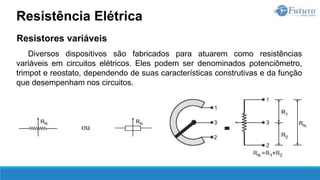


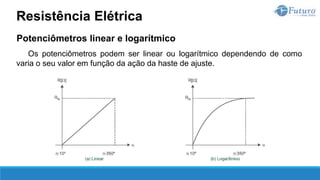


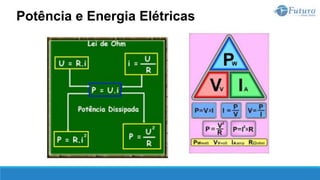
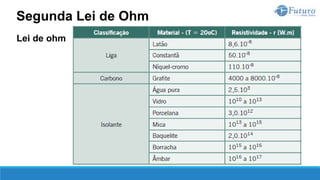
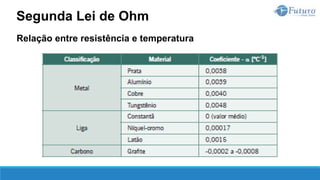
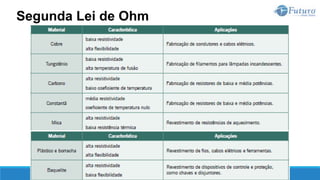
![Lei de ohm
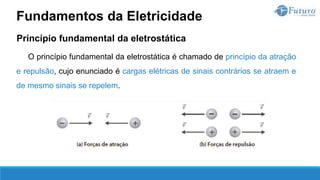
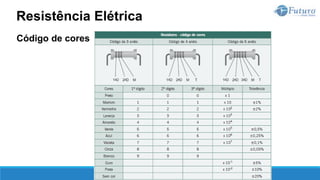
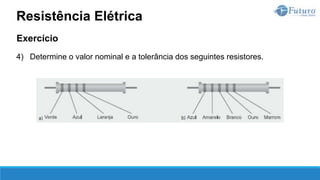
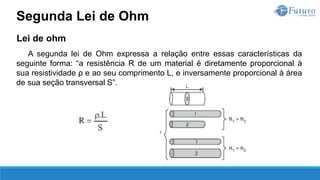
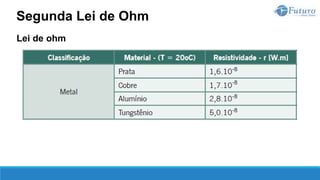
A segunda lei de Ohm estabelece a relação entre a resistência de um
material com a sua natureza e suas dimensões.
Quanto à natureza, um material se caracteriza por sua resistividade, que é
representada pela letra grega ρ (rô), cuja unidade de medida é ohm.metro
[Ω.m].
Quanto às dimensões do material, são importantes o seu comprimento L, em
[m], e a área da seção transversal S, em [m²].
Segunda Lei de Ohm](https://image.slidesharecdn.com/eletricidadebsica-230619042553-dfc05ef2/85/Eletricidade-Basica-pptx-77-320.jpg)






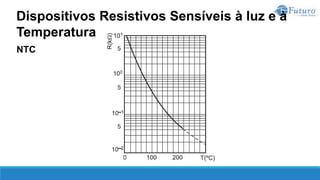
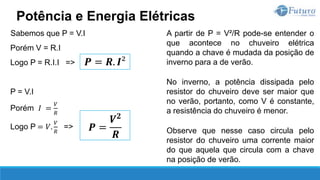
![Potência elétrica
A potência elétrica P, em watt [W], é o produto entre a tensão e a corrente
fornecidas por uma fonte de alimentação ou aplicadas a um dispositivo.
Matematicamente:
Potência produzida por uma fonte de alimentação: 𝑃 = 𝐸. 𝐼
Potência consumida por um dispositivo: 𝑃 = 𝑉. 𝐼
Potência e Energia Elétricas](https://image.slidesharecdn.com/eletricidadebsica-230619042553-dfc05ef2/85/Eletricidade-Basica-pptx-91-320.jpg)