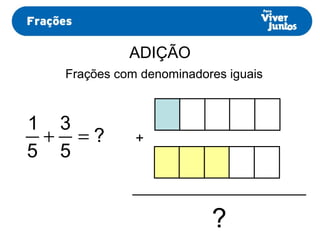
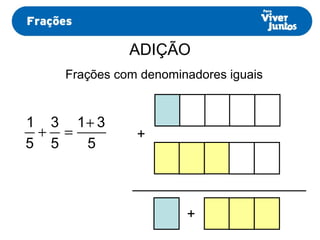
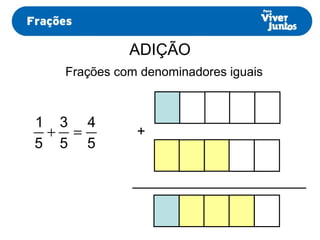
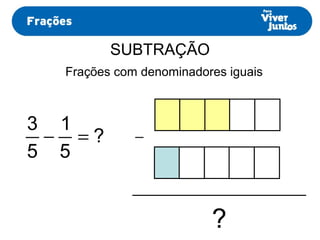
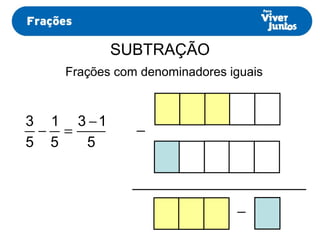
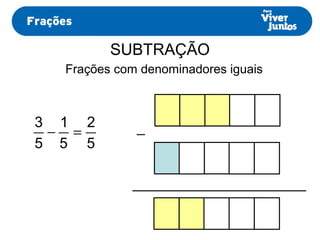
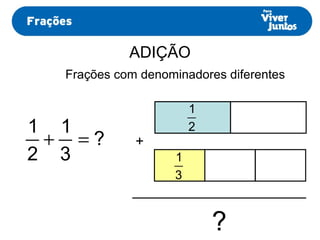
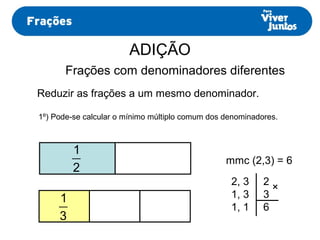
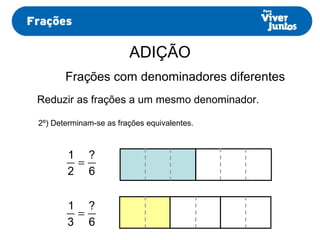
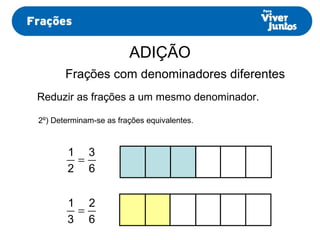
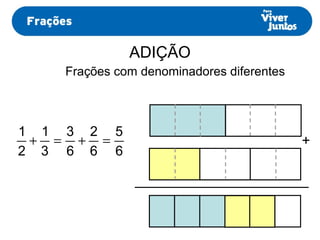
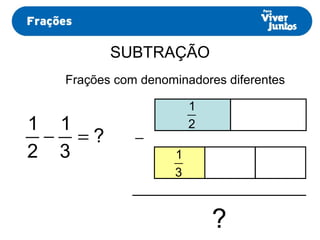
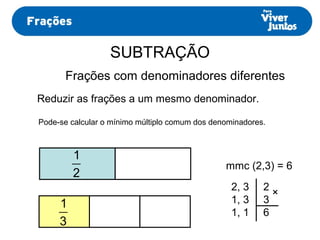
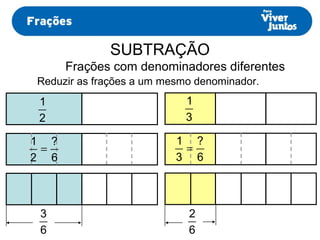
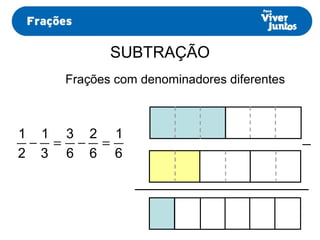
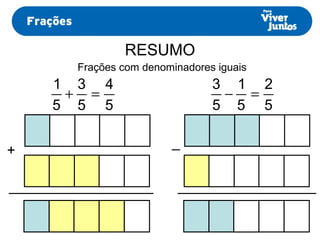
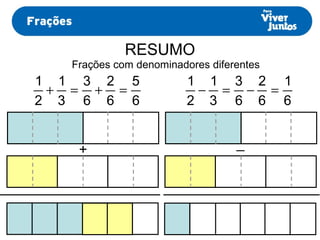
Este documento resume os processos de adição e subtração de frações com denominadores iguais e diferentes. Para frações com denominadores iguais, basta somar ou subtrair os numeradores e manter o denominador comum. Já para frações com denominadores diferentes, é necessário primeiro reduzi-las a um mesmo denominador, calculando o mínimo múltiplo comum dos denominadores originais e, então, proceder com a adição ou subtração.

1. FRAÇÕES
ADIÇÃO E SUBTRAÇÃO

2. ADIÇÃO
?
5
3
5
1
=+ +
?
Frações com denominadores iguais

3. ADIÇÃO
5
31
5
3
5
1 +
=+ +
Frações com denominadores iguais
+

4. ADIÇÃO
5
4
5
3
5
1
=+
Frações com denominadores iguais
+

5. SUBTRAÇÃO
?
5
1
5
3
=− _
?
Frações com denominadores iguais

6. SUBTRAÇÃO
5
13
5
1
5
3 −
=− _
Frações com denominadores iguais
_

7. SUBTRAÇÃO
5
2
5
1
5
3
=− _
Frações com denominadores iguais

8. ADIÇÃO
?
3
1
2
1
=+ +
?
Frações com denominadores diferentes
2
1
3
1

9. ADIÇÃO
Frações com denominadores diferentes
Reduzir as frações a um mesmo denominador.
2
1
3
1
mmc (2,3) = 6
2, 3 2
1, 3 3
1, 1 6
×
1º) Pode-se calcular o mínimo múltiplo comum dos denominadores.

10. ADIÇÃO
Frações com denominadores diferentes
Reduzir as frações a um mesmo denominador.
6
?
2
1
=
2º) Determinam-se as frações equivalentes.
6
?
3
1
=

11. ADIÇÃO
Frações com denominadores diferentes
Reduzir as frações a um mesmo denominador.
6
3
2
1
=
2º) Determinam-se as frações equivalentes.
6
2
3
1
=

12. ADIÇÃO
Frações com denominadores diferentes
6
5
6
2
6
3
3
1
2
1
=+=+ +

13. SUBTRAÇÃO
?
3
1
2
1
=− _
?
Frações com denominadores diferentes
2
1
3
1

14. SUBTRAÇÃO
Frações com denominadores diferentes
Reduzir as frações a um mesmo denominador.
2
1
3
1
mmc (2,3) = 6
2, 3 2
1, 3 3
1, 1 6
×
Pode-se calcular o mínimo múltiplo comum dos denominadores.

15. SUBTRAÇÃO
Frações com denominadores diferentes
Reduzir as frações a um mesmo denominador.
2
1
3
1
6
?
2
1
=
6
?
3
1
=
6
3
6
2

16. SUBTRAÇÃO
Frações com denominadores diferentes
6
1
6
2
6
3
3
1
2
1
=−=− _

17. RESUMO
Frações com denominadores iguais
5
4
5
3
5
1
=+
+
5
2
5
1
5
3
=−
_

18. RESUMO
Frações com denominadores diferentes
6
5
6
2
6
3
3
1
2
1
=+=+
+
6
1
6
2
6
3
3
1
2
1
=−=−
_