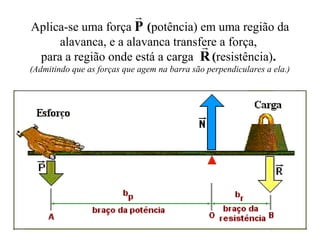
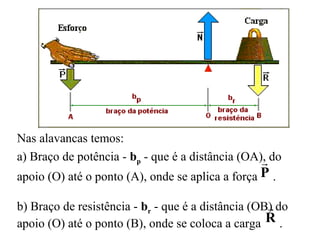
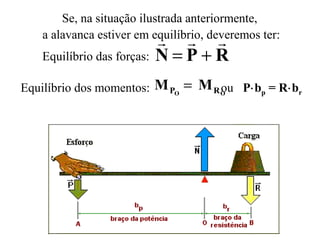
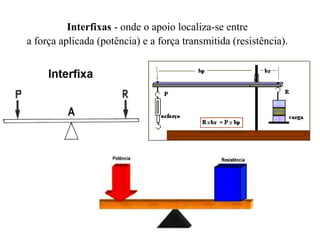
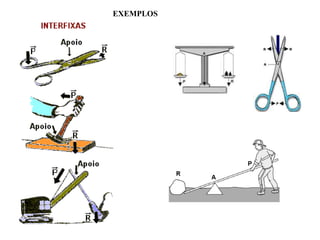
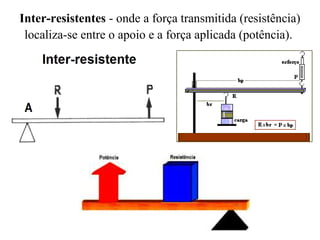
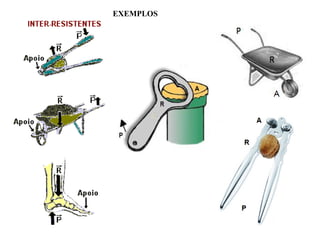
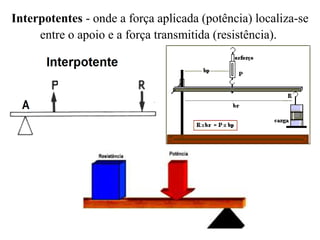
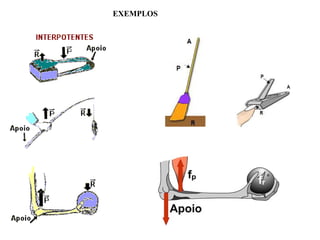
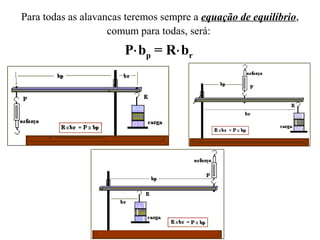
Este documento descreve as alavancas como peças rígidas que giram em torno de um ponto de apoio, transferindo força de um ponto a outro. Explica que as alavancas são classificadas como interfixas, inter-resistentes ou interpotentes dependendo da localização relativa do ponto de apoio, da força aplicada e da carga. Finalmente, resume que para qualquer alavanca em equilíbrio, a força aplicada vezes o braço de potência deve ser igual à carga vezes o braço de resistência.

1. Alavancas

2. Máquinas Simples - Alavancas
São simples peças rígidas (retas ou curvas), capazes de girar ao redor
de um ponto ou eixo, denominado ponto de apoio.

3. Exemplos: Tesouras, alicates, balanças, articulações dos braço e
pernas, remos, gangorras e tantos outros dispositivos funcionam
baseados no princípio das alavancas.

4. Aplica-se uma força (potência) em uma região da
alavanca, e a alavanca transfere a força,
para a região onde está a carga (resistência).
(Admitindo que as forças que agem na barra são perpendiculares a ela.)
P

R


5. Nas alavancas temos:
a) Braço de potência - bp - que é a distância (OA), do
apoio (O) até o ponto (A), onde se aplica a força .
b) Braço de resistência - br - que é a distância (OB) do
apoio (O) até o ponto (B), onde se coloca a carga .
P

R


6. Se, na situação ilustrada anteriormente,
a alavanca estiver em equilíbrio, deveremos ter:
Equilíbrio das forças:
Equilíbrio dos momentos: ou P⋅bp = R⋅br
R P N

+=
OO RP M M =

7. Classificação das alavancas
Dependendo das posições ocupadas pela:
potência (P), apoio (O) e resistência (R),
as alavancas classificam-se em:
Interfixas
Inter-resistentes
Interpotentes

8. Interfixas - onde o apoio localiza-se entre
a força aplicada (potência) e a força transmitida (resistência).

9. EXEMPLOS

10. Inter-resistentes - onde a força transmitida (resistência)
localiza-se entre o apoio e a força aplicada (potência).

11. EXEMPLOS

12. Interpotentes - onde a força aplicada (potência) localiza-se
entre o apoio e a força transmitida (resistência).

13. EXEMPLOS

14. Para todas as alavancas teremos sempre a equação de equilíbrio,
comum para todas, será:
P⋅bp = R⋅br

15. FIM