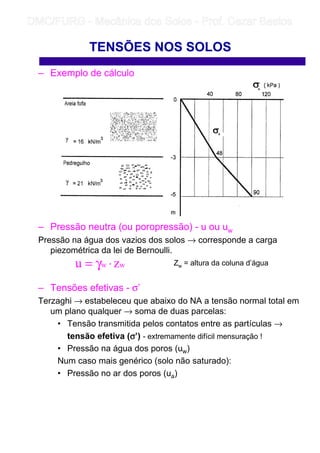
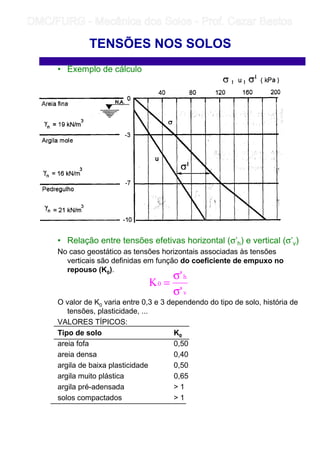
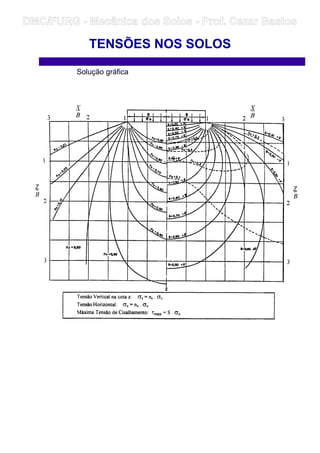
1) O documento discute os conceitos de tensões nos solos, incluindo tensões devido ao peso próprio do solo, tensões efetivas de acordo com o princípio de Terzaghi, e tensões devido a cargas externas.
2) É apresentado o conceito de bulbos de tensões para descrever a propagação e distribuição de tensões em solos devido a cargas aplicadas.
3) São descritas soluções baseadas na teoria da elasticidade, como a solução de Boussinesq para carga concentrada, para estimar tensões em solos.





![– Acréscimo de tensão vertical
ou
onde
Para pontos na vertical abaixo da carga (z/r = 0)
– Acréscimo de tensão horizontal radial
– Acréscimo de tensão transversal
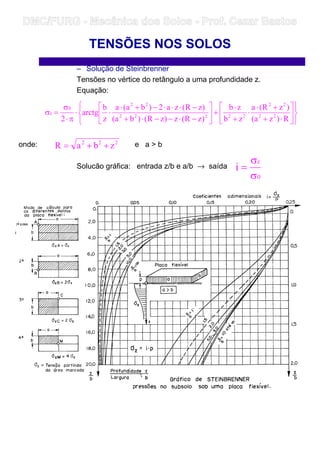
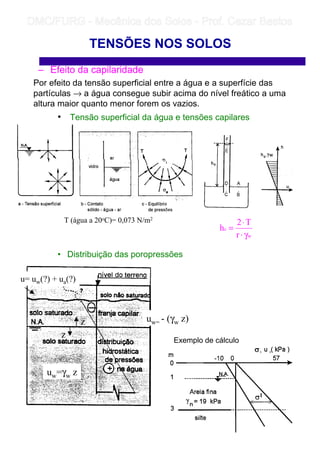
TENSÕES NOS SOLOS
θ⋅
⋅π⋅
⋅
=σ 5
2
z cos
z2
P3
B
2
z N
z
P
⋅=σ
2
z
z
P48,0 ⋅
=σ
]
cos1
cos
21(sencos3[
z2
P 2
3
2
r
θ+
θ
⋅)ν⋅−−θ⋅θ⋅⋅
⋅π⋅
=σ
]
cos1
cos
[cos
z2
P
21(
2
3
2
t
θ+
θ
−θ⋅
⋅π⋅
⋅)ν⋅−−=σ
2
5
2
B
z
r
1
1
2
3
N
+
⋅
π⋅
=
DMC/FURG - Mecânica dos Solos - Prof. Cezar Bastos](https://image.slidesharecdn.com/10-tensoesnosolo-141027154249-conversion-gate02/85/10-tensoes-no-solo-12-320.jpg)
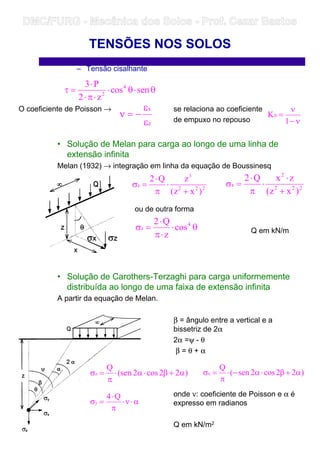
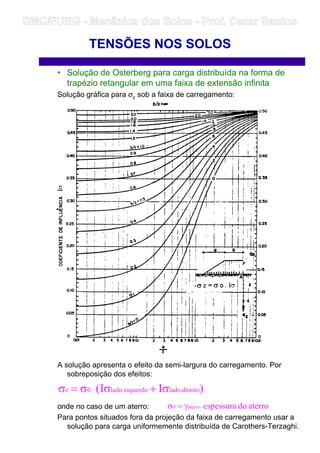
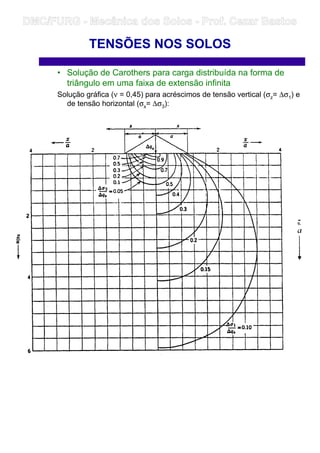
![• Solução de Love para carga uniforme sobre superfície
circular
A fórmula de Love (Love, 1929) obtida a partir da integração da solução
de Boussinesq permite o cálculo do acréscimo de tensão vertical ao
longo da vertical que passa pelo centro de uma placa circular
uniformemente carregada:
Soluções gráficas (para ν = 0,45)
TENSÕES NOS SOLOS
[ ]
+
−⋅σ=σ
2
3
2
0z
)
z
R(1
1
1
DMC/FURG - Mecânica dos Solos - Prof. Cezar Bastos](https://image.slidesharecdn.com/10-tensoesnosolo-141027154249-conversion-gate02/85/10-tensoes-no-solo-17-320.jpg)
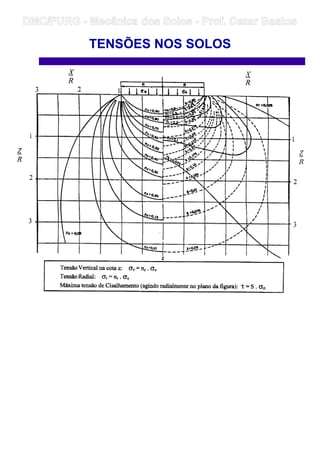
![• Soluções para carga uniforme sobre superfície retangular
– Solução de Newmark
Newmark (1933) → a partir da integração da equação de
Boussinesq, solução para o cálculo das tensões provocadas no
interior do semi-espaço infinito de superfície horizontal por
carregamento uniformemente distribuído numa área retangular.
Equação:
Solução gráfica:
entrada: m e n → tem-se Iσ
Com base no Princípio da Superposição dos Efeitos é possível determinar
as tensões em qualquer outro ponto sob a placa ou fora dela.
TENSÕES NOS SOLOS
σ⋅σ=σ I0z
z
a
m =
z
b
n =
[ ]
⋅−++
++⋅⋅⋅
+
++⋅⋅+++
++⋅++⋅⋅⋅
⋅
π⋅
σ
=σ 2222
5,022
222222
225,022
0
z
nm1nm
)1nm(nm2
arctg
)1nm()nm1nm(
)2nm()1nm(nm2
4
DMC/FURG - Mecânica dos Solos - Prof. Cezar Bastos](https://image.slidesharecdn.com/10-tensoesnosolo-141027154249-conversion-gate02/85/10-tensoes-no-solo-19-320.jpg)