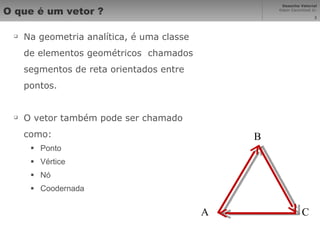
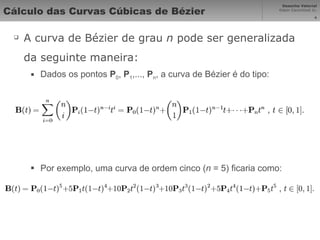
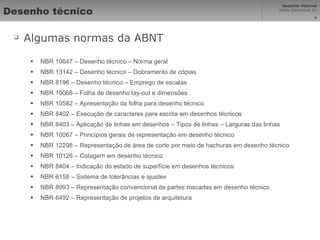
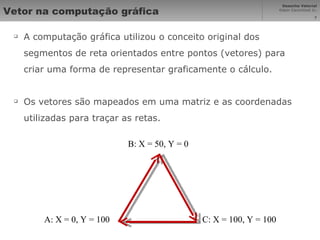
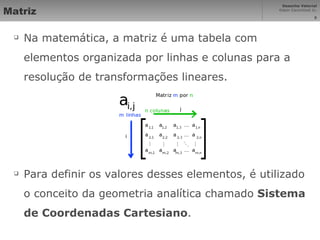
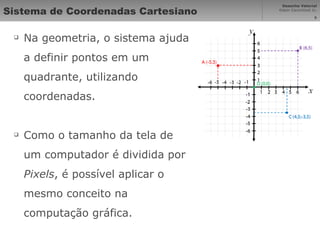
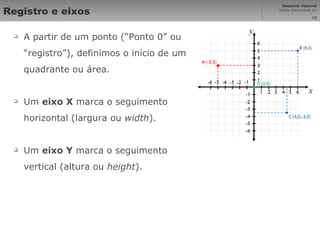
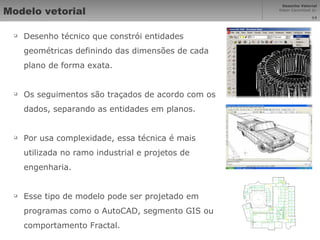
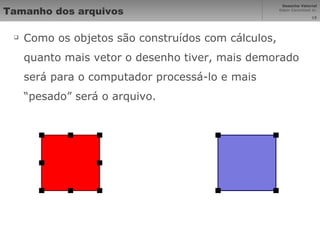
Vetores são segmentos de reta orientados entre pontos que representam elementos geométricos. Curvas de Bézier são curvas polinomiais que interpolam pontos de controle. Desenho técnico usa ciências exatas para garantir proporções corretas em imagens projetadas. Sistemas de coordenadas cartesiana mapeiam pontos em uma matriz para representar vetores graficamente na computação gráfica.

1. Vetor Introdução a arte vetorial

2. O que é um vetor ? Na geometria analítica, é uma classe de elementos geométricos chamados segmentos de reta orientados entre pontos. O vetor também pode ser chamado como: Ponto Vértice Nó Coodernada A B C

3. Curva de Bézier Curva polinomial expressa como a interpolação linear entre alguns pontos representativos, chamados de pontos de controle. Criada em 1962 pelo francês Pierre Bézier, funcionário da Renault, que a usou para o design de automóveis, baseado no Algoritmo de De Casteljau em 1957.

4. Cálculo das Curvas Cúbicas de Bézier A curva de Bézier de grau n pode ser generalizada da seguinte maneira: Dados os pontos P 0 , P 1 ,..., P n , a curva de Bézier é do tipo: Por exemplo, uma curva de ordem cinco ( n = 5) ficaria como:

5. Desenho técnico Baseado na teoria dos Elementos de Euclides , é uma forma de linguagem usada por artistas para “projetar” uma imagem. Utiliza ciências exatas para garantir que as proporções estejam corretas.

6. Desenho técnico Algumas normas da ABNT NBR 10647 – Desenho técnico – Norma geral NBR 13142 – Desenho técnico – Dobramento de cópias NBR 8196 – Desenho técnico – Emprego de escalas NBR 10068 – Folha de desenho lay-out e dimensões NBR 10582 – Apresentação da folha para desenho técnico NBR 8402 – Execução de caracteres para escrita em desenhos técnicos NBR 8403 – Aplicação de linhas em desenhos – Tipos de linhas – Larguras das linhas NBR 10067 – Princípios gerais de representação em desenho técnico NBR 12298 – Representação de área de corte por meio de hachuras em desenho técnico NBR 10126 – Cotagem em desenho técnico NBR 8404 – Indicação do estado de superfície em desenhos técnicos NBR 6158 – Sistema de tolerâncias e ajustes NBR 8993 – Representação convencional de partes roscadas em desenho técnico NBR 6492 – Representação de projetos de arquitetura

7. Vetor na computação gráfica A computação gráfica utilizou o conceito original dos segmentos de reta orientados entre pontos (vetores) para criar uma forma de representar graficamente o cálculo. Os vetores são mapeados em uma matriz e as coordenadas utilizadas para traçar as retas. A: X = 0, Y = 100 B: X = 50, Y = 0 C: X = 100, Y = 100

8. Matriz Na matemática, a matriz é uma tabela com elementos organizada por linhas e colunas para a resolução de transformações lineares. Para definir os valores desses elementos, é utilizado o conceito da geometria analítica chamado Sistema de Coordenadas Cartesiano .

9. Sistema de Coordenadas Cartesiano Na geometria, o sistema ajuda a definir pontos em um quadrante, utilizando coordenadas. Como o tamanho da tela de um computador é dividida por Pixels , é possível aplicar o mesmo conceito na computação gráfica.

10. Registro e eixos A partir de um ponto (“Ponto 0” ou “registro”), definimos o início de um quadrante ou área. Um eixo X marca o seguimento horizontal (largura ou width ). Um eixo Y marca o seguimento vertical (altura ou height ).

11. Vetorização Existem duas técnicas básicas na vetorização de imagens que são aplicáveis em qualquer programa: Modelagem dos vértices Vetorização pela forma

12. Modelagem dos vértices São criados pontos em volta da imagem, editando as curvas das vértices até reproduzir a forma desejada. Esse processo é similar a técnica de modelagem de uma escultura.

13. Vetorização pela forma Utilizando conceitos da Gestalt , observasse se o objeto possui formas geométricas =

14. Modelo vetorial Desenho técnico que constrói entidades geométricas definindo das dimensões de cada plano de forma exata. Os seguimentos são traçados de acordo com os dados, separando as entidades em planos. Por usa complexidade, essa técnica é mais utilizada no ramo industrial e projetos de engenharia. Esse tipo de modelo pode ser projetado em programas como o AutoCAD, segmento GIS ou comportamento Fractal.

15. Tamanho dos arquivos Como os objetos são construídos com cálculos, quanto mais vetor o desenho tiver, mais demorado será para o computador processá-lo e mais “pesado” será o arquivo.

16. Forma e contorno Para aplicar o contorno (ou borda) no objeto, o programa, depois de calcular a área da forma, realiza um outro cálculo em sua extremidade para adicionar o contorno. Isso significa que ele cria um outro objeto anexado na extremidade da foram. Por este motivo, o contorno acaba sendo um outro objeto separado da forma e devemos tomar cuidado com isso.

17. Programas vetoriais mais comuns Proprietários AutoCAD Corel Draw Adobe Flash Illustrator FreeHand Photoshop 3D Studio Max Swift3D Lightwave Maya Microsoft Office Word Excel PowerPoint Etc... Livres (GNU) GIMP Inkscape OpenOffice.org Draw Google Docs Blender NodeBox Synfig Muan sk1

18. Créditos As informações contidas nessa apresentação foram elaboradas com base na minha experiência profissional que, em algum momento, podem contradizer o que é explicado na teoria. Parte deste material foi selecionada na bibliografia oficial da disciplina e na bibliografia complementar que de disponibilizei durante a aula. Existem algumas informações que também podem ser encontradas na Wikipédia. Porém, como seu conteúdo pode ser alterado por qualquer pessoa, sua credibilidade pode ser questionada. Só utilize informações da Wikipédia se você já conhece o assunto e concorda com as definições.

19. Vetor Introdução a arte vetorial Odair Cavichioli Júnior http://cavichioli.blogspot.com/