O documento discute a representação e interpolação de rotações em computação gráfica, destacando o uso de quaternions e a fórmula de Rodrigues como soluções para problemas de ambiguidade encontrados com ângulos de Euler. Ele aborda a eficácia das coordenadas homogêneas para representar transformações afins e os desafios da interpolação entre eixos de rotação. Vantagens e desvantagens de diferentes métodos, como gimball-lock e a interpolação esférica, também são discutidas, fornecendo uma visão abrangente das técnicas de animação em 3D.

1. Computação Gráfica
prof. Edilson Aguiar
Universidade Federal do Espírito Santo
Centro Universitário Norte do Espírito Santo
Eliezer de Souza da Silva

2. Visualização de objetos 3D.
Animação (key framing):
• Computador faz a interpolação entre os key frames.
Translações podem ser feitas com interpolação linear ou
splines.splines.
Rotações são mais complicadas.
Problema: que estrutura matemática
captura de maneira ideal operações de
rotação no espaço, facilitando a
implementação computacional?

3. Teorema de Euler [2,3]:
• “Dados dois pontos no espaço existe um eixo no espaço e um ângulo
de rotação que leva um ponto ao outro” ou “o movimento de um corpo
rígido no espaço com um ponto fixo é uma rotação”.

4. Fórmula de Rodrigues [2,3,5]

5. Ângulos de Euler utilizando matriz de
rotação: parametrização do espaço
através de três eixos de rotação.
• Esta parametrização é ambígua.• Esta parametrização é ambígua.
Quaternions: encapsula diretamente o
Teorema de Euler.

6. Euler utilizou inicialmente para resolver as equações
de movimento (separação de variáveis) [1].
• Pressuposto: o espaço de rotações pode ser totalmente
parametrizado por três operações de rotação em eixos
perpendiculares.

7. Exemplo 2D

8. Implementação das rotações associadas a
cada eixo através de uma matriz de rotação.
• Coordenadas homogêneas: permite a
representação de transformações afins na forma
matricial (possibilita a composição de rotações e
outras operações afins naturalmente).outras operações afins naturalmente).

9. Desvantagens:
• A escolha dos eixos é arbitrária e existem diversas
possibilidades de multiplicação das matrizes de rotação e
nem todas são geometricamente intuitivas.
• A representação do espaço de rotações através de
ângulos de Euler é ambígua (problema inverso não é
bem formulado – rotação gerada por diferentes triplas de
ângulos de Euler).ângulos de Euler).
• Gimball-Lock: degeneração dos graus de liberdade.
• A interpolação não é boa, nem fácil (cada eixo é
interpolado de modo independente).
Vantagens:
• Matemática das matrizes é bem conhecida e estudada,
além de ter bastante implementações.
• Coordenadas homogêneas permite representação de
todas as transformações afins básicas

10. Trata-se de uma álgebra descoberta por
Sir Willian Hamilton como uma
generalização dos complexos para
espaços de ordens maiores.espaços de ordens maiores.

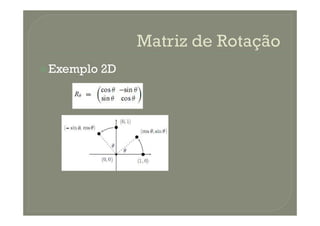
11. Espaço de Rotações do R3: SO(3) (Matrizes Ortonormais)
Espaço da esfera unitária de quaternions S3 tem um
mapeamente 2 por 1 em SO(3). (q e –q correspondem ao
mesmo ponto)[1,2]
Utilizando a esfera unitária obtemos diretamente a fórmula
de Rodrigues.
Temos uma implementação direta de uma rotação de p em θ
graus ao longo do eixo v utilizando quaternions.

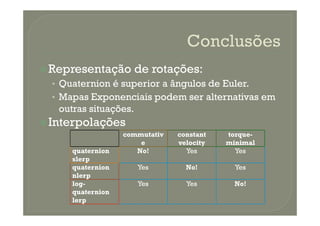
12. Spherical Linear Interpolation [1]:
• Não-comutativo.
• Velocidade constante na esfera.
• Geodésico (Torque mínimo).• Geodésico (Torque mínimo).

13. É ótimo somente entre dois pontos [1,2]
• Shoemake sugere um esquema parecido com a geração
de curvas de Bezier sobre a superfície da esfera.

14. Squad (Spherical Spline Quaternion Interpolation)
[2]
Nlerp (Normalized Quaternion Slerp):
• Comutativo, geodésico, mas não tem velocidade constante.

15. Quaternions apresentam problemas caso eu
tenho que ser derivado (controle
diferencial, ou otimizador, por exemplo).
• D(q) pertence ao plano tangente à esfera unitária.• D(q) pertence ao plano tangente à esfera unitária.
Preciso controlar para impedir que ele “saia”.[4]
Mapas exponenciais:
• Sabemos onde se encontram as singularidades
(evitamos-as)[4].
• R3 → S3 ; S3 → SO(3)
• Inverso: log map

16. Representação de rotações:
• Quaternion é superior a ângulos de Euler.
• Mapas Exponenciais podem ser alternativas em
outras situações.outras situações.
Interpolações
commutativ
e
constant
velocity
torque-
minimal
quaternion
slerp
No! Yes Yes
quaternion
nlerp
Yes No! Yes
log-
quaternion
lerp
Yes Yes No!

17. [1] SHOEMAKE, K. Animating Rotations with Quaternion Curves. Computer Graphics
(SIGGRAPH ’85 Proceedings), volume 19, pages 245-254, July 1985.
[2] DAM, E.B; KOCH, M. and LILLHOLM, M. Quaternions,Interpolation and
Animation.Technical Report DIKU-TR-98/5. University of Copenhagen. 1998.
Denmark.
[3] GOLDSTEIN, H; POOLE, C; SAFKO, J. Classical Mechanics, 3rd Edition.
Addison-Wesley. 2000. New York.
[4] GRASSIA,F.S. Practical parameterization of rotations using the exponential map,[4] GRASSIA,F.S. Practical parameterization of rotations using the exponential map,
Journal of GraphicsTools, volume 3.3, 1998. Disponível em
http://graphics.snu.ac.kr/OpenGL2003/10(1112)/expmap.pdf (31/05/2011)
[5]VINCE, J. RotationTransforms For Computer Graphics. Springer-Verlag. London (UK).
2011.
[6]ANGEL, E. Interactive Computer Graphics –ATop Down Approach Using
OpenGL, 3rd Edition.Addison-Wesley. 2003.
[7] Jonathan Blow. Understanding Slerp,Then Not Using It.Disponível em
http://number-
none.com/product/Understanding%20Slerp,%20Then%20Not%20Using%20It