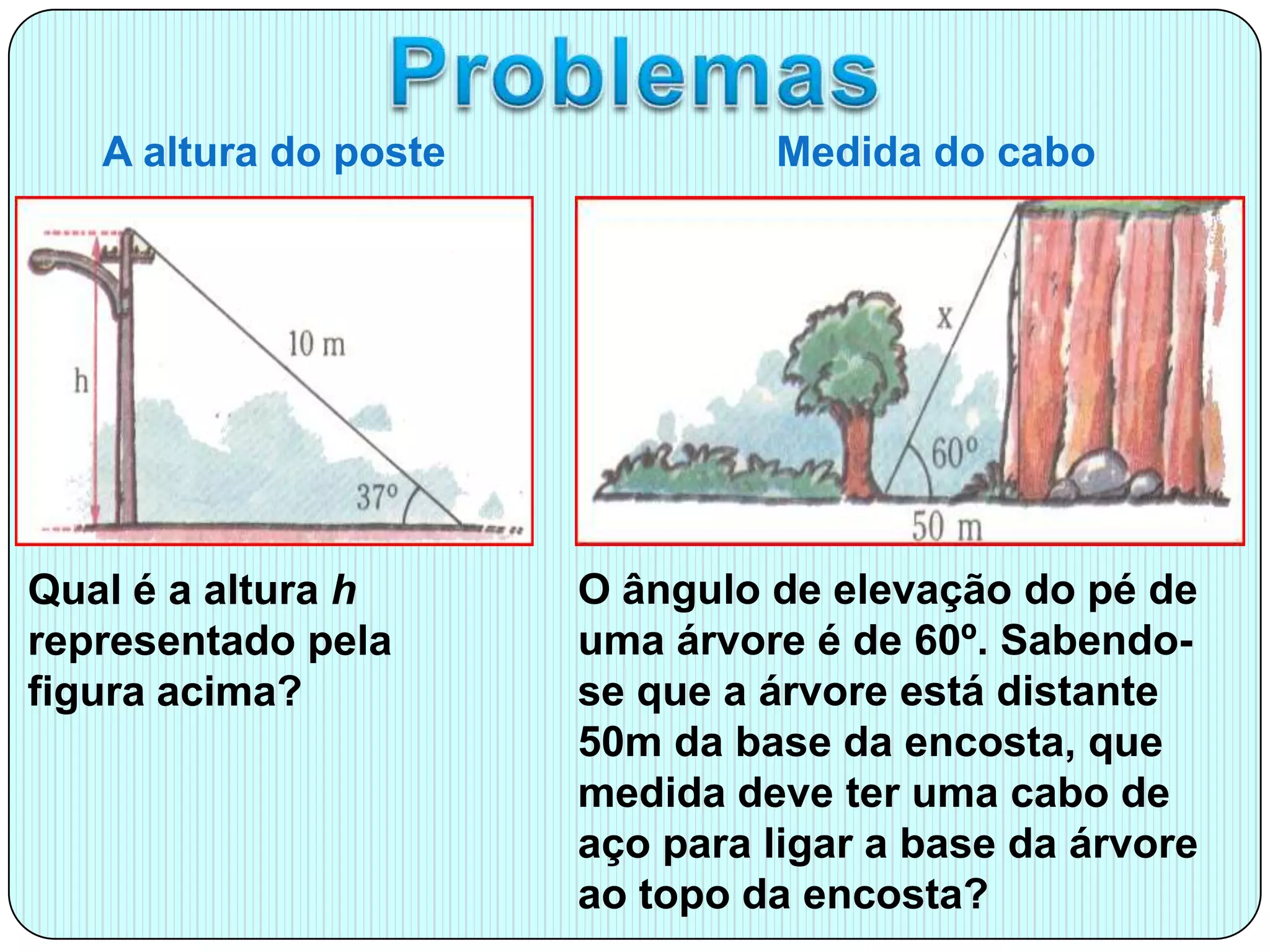
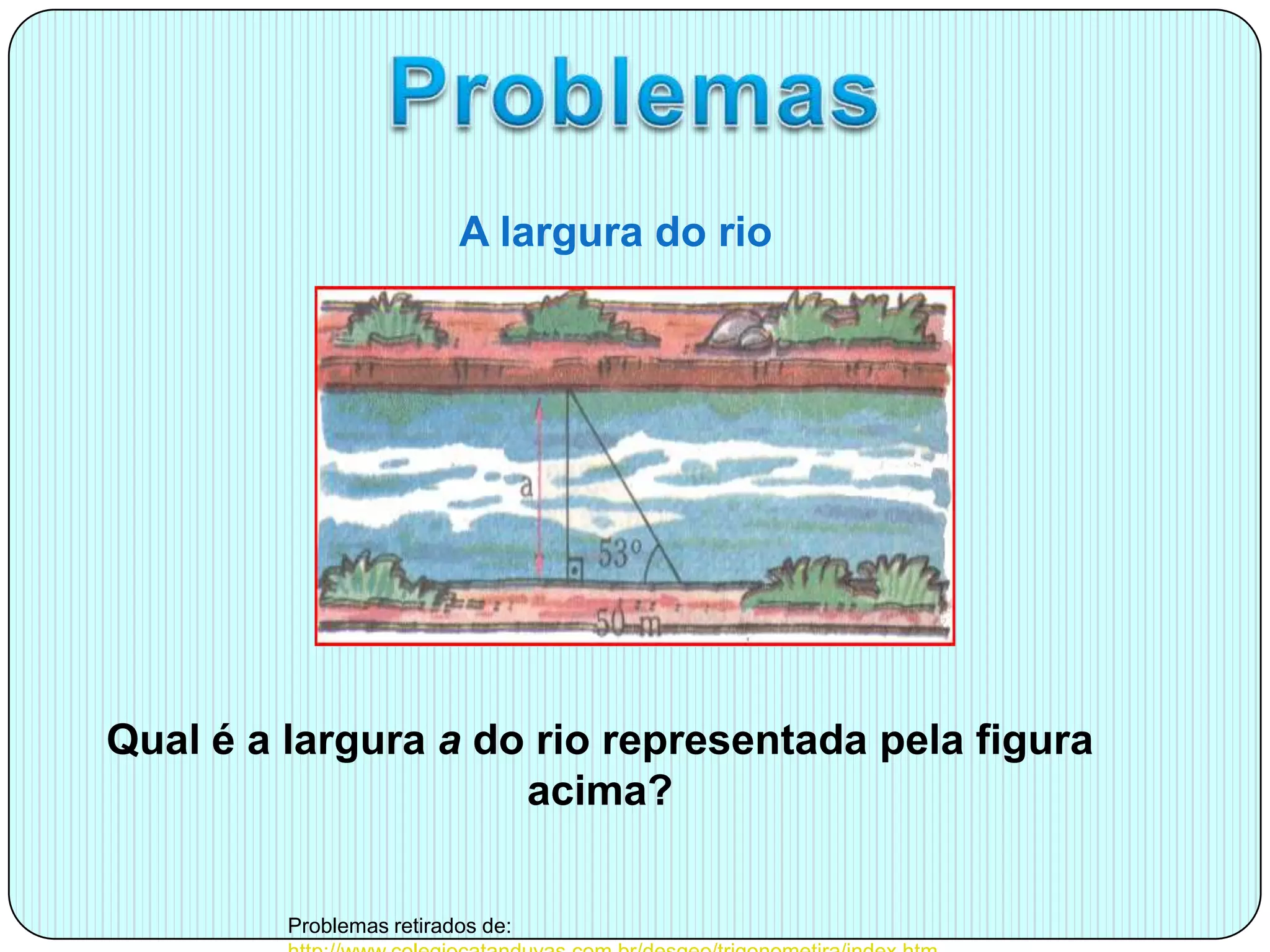
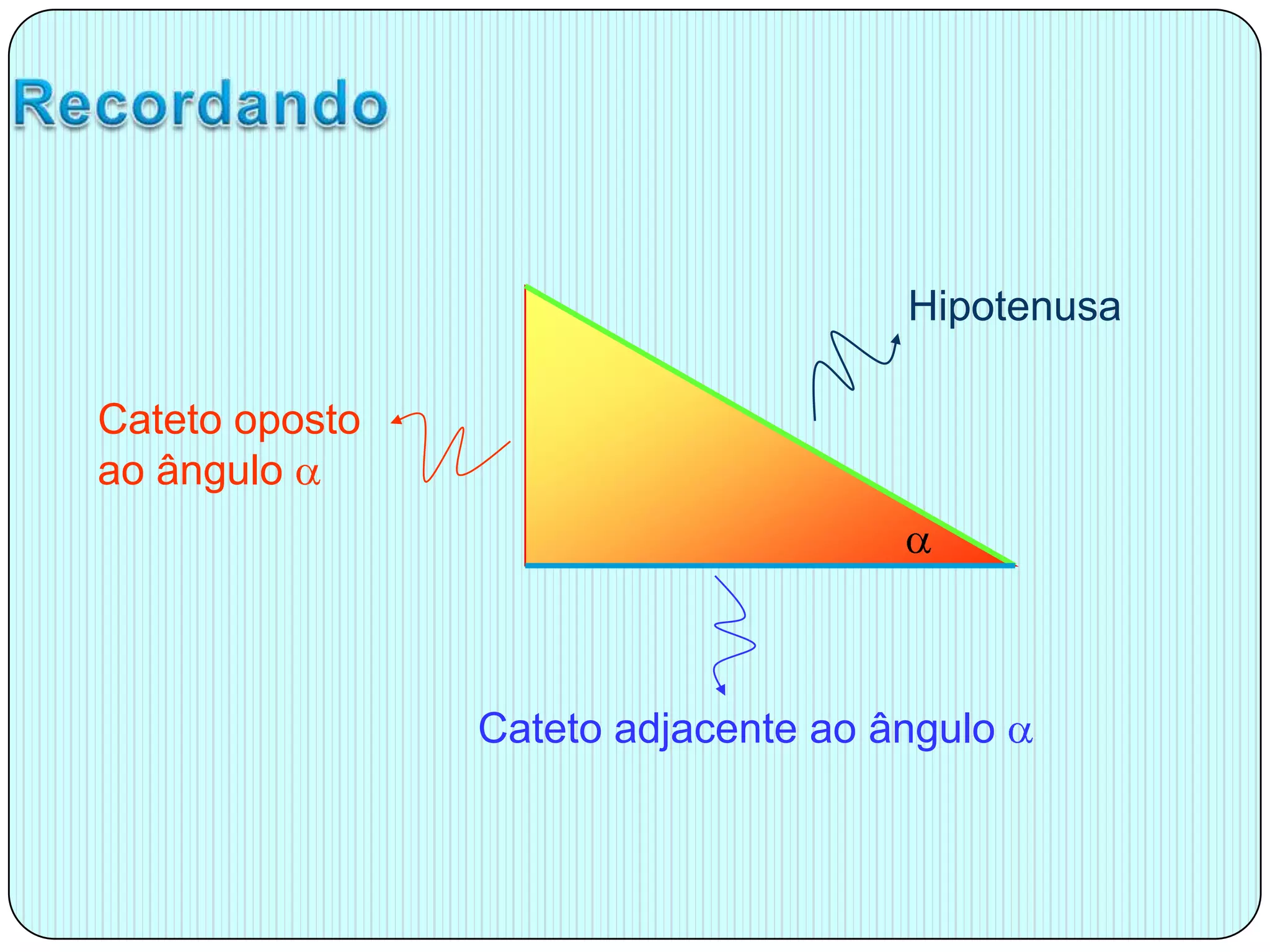
O documento apresenta um relembrar das razões trigonométricas, destacando a relação entre seno, cosseno e tangente em triângulos retângulos. Também oferece dicas para resolver problemas de trigonometria e apresenta exemplos práticos, como calcular a altura de uma árvore e a largura de um rio. Além disso, menciona a conexão da trigonometria com áreas como astronomia e navegação.

1. TrigonometriaImagem retirada de: http://www.colegiocatanduvas.com.br/desgeo/trigonometira/index.htm

2. Pretende-se com esta apresentação que sejam relembradas as razões trigonométricas, sendo indicados alguns problemas que podem ser resolvidos através da utilização das mesmas.

3. RecordandoHipotenusa Cateto oposto ao ângulo Cateto adjacente ao ângulo 

4. CcbBaARazões TrigonométricasSendo [ABC] um triângulo rectângulo e a amplitude de um dos seus ângulos agudos, define-se:

5. CcbBaARelações entre as razões trigonométricasRelação entre o seno, o co-seno e a tangente de um mesmo ângulo Dado o triângulo [ABC], sabemos por definição que:Vamos calcular o seguinte quociente:Concluímos então que:

6. Problemas de Trigonometria

7. Dicas para se resolver problemas usando TrigonometriaLer o problema com atençãoVerificar quais os dados disponibilizados no problema Verificar o que se pretende obterTer em mente as razões trigonométricas resolvendo o problema de acordo com os dados disponibilizados e com aquilo que se pretende calcular

8. ProblemasA altura do posteMedida do caboO ângulo de elevação do pé de uma árvore é de 60º. Sabendo-se que a árvore está distante 50m da base da encosta, que medida deve ter uma cabo de aço para ligar a base da árvore ao topo da encosta?Qual é a altura h representado pela figura acima?

9. ProblemasA largura do rioQual é a largura a do riorepresentada pela figura acima?Problemas retirados de: http://www.colegiocatanduvas.com.br/desgeo/trigonometira/index.htm

10. Algumas imagens “da Trigonometria”Sabemos que está ligada à Astronomia, que ajuda a prever eclipses, a estimar equinócios, a estabelecer calendários, dados de navegação, etc.Imagens encontradas pela pesquisa no Google

11. FIM