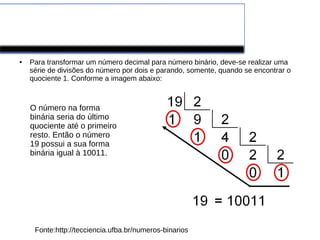
O documento discute sistemas numéricos utilizados em computação, incluindo conversões entre binário, decimal, octal e hexadecimal. Também explica a tabela ASCII, que padroniza a representação de caracteres para permitir a comunicação entre computadores.

1. Arquitetura e
Manutenção de
Computadores

2. Conversão Entre
sistemas Numéricos
● A conversão entre sistemas numéricos é feita com base em
algumas regras e serve para que se obtenha o valor de um
elemento no sistema numérico mais adequado a cada
situação. Entre os sistemas numéricos mais utilizados na
computação há o binário, decimal, octal e sistema
hexadecimal. Cada um destes apresentando sua própria
faixa de valores possíveis, e cada um possui uma aplicação
específica, dentro da Ciência da Computação.

3. Tabela ASC
● Antes de 1960 a maioria dos sistemas de computadores tinha uma maneira
particular de representar os caracteres alfanuméricos. Ou seja, cada marca
de computador e, até, cada modelo, usava um código próprio para
representar cada letra, número e todos os símbolos que usamos.
● Assim, foi proposto o uso de um código comum, utilizado por todos, a fim de
possibilitar a comunicação entre os computadores, objetivando permitir a
troca de dados entre máquinas de diferentes tipos e fabricantes.
● O "American National Standards Institute" aceitou a proposta de Robert
William Bemer e sua equipe para desenvolver o "American Standard Code for
Information Interchange" (Código Padrão Norte-americano para Intercâmbio
de Informações), hoje conhecido como código ASCII.
Fonte: http://www.ufpa.br/dicas/progra/arq-asc.htm

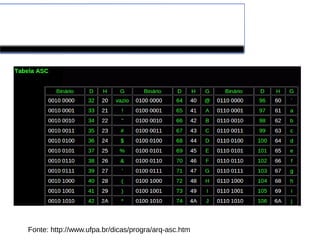
4. Tabela ASC
●
Portanto, ASCII é um código numérico usado para representar os caracteres,
entendido por quase todos os computadores, impressoras e programas de edição de
texto, que usa a escala do decimal 0 a 127.
●
É baseado no alfabeto romano, como é usado no idioma inglês moderno, e visa
padronizar a forma pela qual os computadores representam letras, números, acentos
e sinais diversos ( por exemplo: <, {, ] ) e alguns códigos de controle ( <Crtl> ) que
são utilizados para converter todos os símbolos em números binários, os quais
efetivamente podem ser processados.
Fonte: http://www.ufpa.br/dicas/progra/arq-asc.htm

5. Tabela ASCII
● O código permite não só uma melhor compreensão sobre a lógica do
funcionamento do computador mas, também, possibilita a utilização de
caracteres, cujos símbolos não aparecem no teclado.
● É importante notar que há apenas 95 caracteres que podem ser impressos. E
eles são numerados de 32 a 126 pois os primeiros códigos (de 0 a a 31)
foram reservados para caracteres de controle, ou seja, que controlam
funções ou equipamentos. Esses caracteres de controle tiveram sua origem
nos primórdios da computação, quando eram utilizadas máquinas Teletype
(como máquinas de escrever eletro-mecânicas), fitas de papel perfurado e
impressoras de cilindro, portanto muitos deles são dirigidos a estes
equipamentos. Por exemplo:
– o caráter 10 representa a função "LINE FEED", que faz com que uma impressora
avance seu papel,
– o caráter 24 representa a função "cancel",
– o caráter 27 representa a função "escape" determinada pela tecla <ESC>,
encontrada no canto superior esquerdo nos teclados.
Fonte: http://www.ufpa.br/dicas/progra/arq-asc.htm

6. Tabela ASCII
Fonte: http://www.ufpa.br/dicas/progra/arq-asc.htm

7. Tabela ASCII
Fonte: http://www.ufpa.br/dicas/progra/arq-asc.htm

8. Números Binários
● Os computadores se comunicam e processam as
informações através de Códigos Binários. Ou
seja, os computadores só utilizam dois dígitos,
como por exemplo: 0 ou 1 e passa corrente ou
não. No entanto, como é possível, utilizando
somente os números binários, estabelecer
comunicação entre os computadores? É
interessante entender como se estabelecem essa
comunicação.
Fonte:http://tecciencia.ufba.br/numeros-binarios

9. Números Binários
●
O sistema binário ou de base 2 é um sistema de numeração posicional em que todas as
quantidades se representam com base em dois números, ou seja, zero e um (0 e 1).
●
Os computadores digitais trabalham internamente com dois níveis de tensão, pelo que o
seu sistema de numeração natural é o sistema binário. Com efeito, num sistema simples
como este é possível simplificar o cálculo, com o auxílio da lógica booliana. Em
computação, chama-se um dígito binário (0 ou 1) de bit, que vem do inglês Binary Digit.
Um agrupamento de 8 bits corresponde a um byte (Binary Term). Um agrupamento de 4
bits, ainda, é chamado de nibble.
Fonte:http://tecciencia.ufba.br/numeros-binarios

10. Números Binários
● DEFINIÇÃO
– "Conjunto de duas forças iguais, mas contrárias, que atuam no extremo
de uma reta.(...) Diz-se do sistema de numeração que tem por base 2."
São duas definições feitas pelo dicionário Aurelio, entre outras, sobre
binário, na sua versão on-line (http://www.dicionariodoaurelio.com/).
– "Diz-se do sistema de numeração que tem por base 2"
● Partindo dos conceitos, pode-se dizer que os números binários
são representados utilizando apenas dois dígitos. Os dígitos
padrões que formam os números binários são os 0 e 1.
Fonte:http://tecciencia.ufba.br/numeros-binarios

11. CONVERSÕES DE DECIMAIS
PARA BINÁRIOS
● Para transformar um número decimal para número binário, deve-se realizar uma
série de divisões do número por dois e parando, somente, quando se encontrar o
quociente 1. Conforme a imagem abaixo:
Fonte:http://tecciencia.ufba.br/numeros-binarios
O número na forma
binária seria do último
quociente até o primeiro
resto. Então o número
19 possui a sua forma
binária igual à 10011.

12. CONVERSÕES DE BINÁRIOS
PARA DECIMAIS
● Para converter os números binários em números decimais deve-se somar o produto
do dígito binário e dois elevado a posição do dígito, conforme a imagem abaixo:
Fonte:http://tecciencia.ufba.br/numeros-binarios
Como visto acima, o número 01100 corresponde à 12 em número
decimal.

13. Exercícios classe
● 1. Converta para Decimal
– a)10011
– b) 11100010
– c) 1000001
● 2. Converta para Binário
– a) 23;
– b) 2615;
– c) 25;

14. Exercício para Casa
1. Converta os números seguintes entre as bases
indicadas.
a. De Decimal para Binário.
-77(10)
-189(10)
-234(10)
b. De Binário para Decimal.
-11001(2)
-101101011(2)
-10001111(2)
•

15. Exercício para Casa
2. calcule os números binários que se
seguem a resposta em binário.
a. 10101(2) + 11001(2)
b. 11001011(2) + 100110(2)
c. 1011001(2) + 110011(2)

16. Hexadecimal para
Decimal
● Composto por 16 símbolos ou numerais;
● Base 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B,
C, D, E, F.

17. Conversão Decimal para
Hexadecimal

18. EXERCÍCIOS
● Converta para Decimal
● a) 1AF
● b) AFF
● c) 20CC
● d) 12FF

19. EXERCÍCIOS
● Converta para Hexadecimal
● a) 1024
● b) 10
● c) 2030
● d) 100