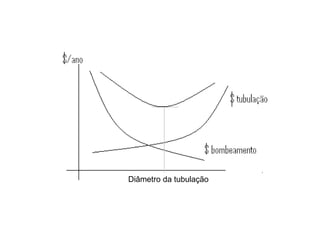
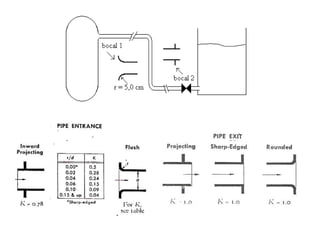
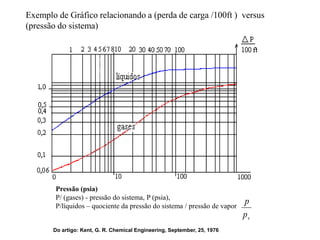
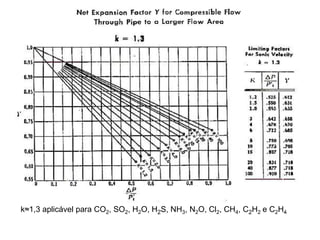
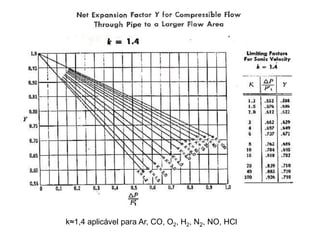
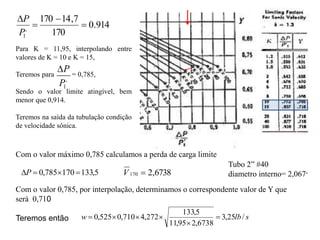
1) O documento discute conceitos de dimensionamento de tubulações como diâmetro, viscosidade, densidade e vazão. 2) São apresentadas fórmulas para calcular perda de carga em função da viscosidade, diâmetro e comprimento da tubulação. 3) Exemplos numéricos ilustram o cálculo do diâmetro mínimo e dimensionamento de tubulações para diferentes fluidos.

1. Dimensionamento de tubulações
Parte II

2. Diâmetro da tubulação

3. VISCOSIDADE
 Viscosidade absoluta μ
Poise (P), usual centipoise 10-2 poise
1μ = 1dyn seg/cm2 , ou g/cm.s, ou kg/ms = Pa.s (1 cP = 10-3 Pa.s) 1P = 10-5 Pa.s
 Viscosidade cinemática υ,
Stoke, usual centistoke 10-2 stokes
υ = μ / ρ ( cm2/s) ρ =g/cm3
Propriedades físicas de fluidos
Variação da viscosidade com a temperatura:
 Líquidos: T ↑ μ ↓ ,
 Gases: T ↑ μ ↑

4. DENSIDADE
 Densidade específica
 Líquidos: lb/ft3, g/cm3
Viscosímetros cinemáticos:
Saybolt universal - Tempo (s) necessário para escoamento através de um orifício
Saybolt Furol (para fluidos muito viscosos)
Engler
Saybolt Redwood
Brookfield (spinder)
Ostwald
Esferas em duto, etc..

5.  De: API (óleos)
API
d 0
5
,
131
5
,
141

 d - (60F/60F)
CONVERSÃO DE OUTRAS UNIDADES PARA DENSIDADE RELATIVA:
 De: Bé (Baumé)
• Líquidos menos densos que a água:
Bé
d 0
130
140


 Líquidos mais densos que a água:
Bé
d 0
145
145


)
(
)
(
ar
Mol
gas
Mol
d 
Gases e vapores
Densidade relativa

6. 
1
_

V
 
*
P
A
R ft
H 
Volume específico
Outras Termos ou parâmetros /definições:
Para dutos não circulares:
 Raio hidráulico:
Deq= 4. RH (ft) ou 48 RH , se em (pol)
cm3/g ou ft3/lb
A = área da seção transversal do duto - ft2
P* = perímetro molhado -ft
 Diâmetro equivalente

7.   2
2
min
/ 65
,
19
fL
D
h
d
q
eq
L
gal 

L
h
DETERMINAÇÃO DA VAZÃO EM DUTOS NÃO CIRCULARES
– ou parcialmente preenchidos
SEÇÃO NÃO CIRCULAR *
 Deq ( ft ) – diâmetro equivalente
 perda de carga estática devido ao fluxo através do duto (inclinação) ft/ft (ΔH)
 d - diâmetro de um tubo que tenha seção equivalente à seção transversal de líquido (pol)
** unidades inglesas
* retangulares, ovais, circulares parcialmente preenchidos, externo a feixe tubular,
etc..
**

8. 3
/ m
kg



h
m
Q /
3


 LÍQUIDOS DE BAIXA VISCOSIDADE –
Critério - Velocidade econômica
Diâmetro mínimo
2
1
6
1
.
min 1
,
3 Q
D 

  (mm)
Diâmetro típico
Determinando diâmetro econômico
434
.
0
52
,
15 Q
DT 
 (mm)

9. LÍQUIDOS DE MÉDIA / ALTA VISCOSIDADE
Critério – perda de carga econômica
Velocidade de 1,5 a 3,5 m/s
*alta viscosidade: velocidade de 0,5 a 1,5 m/s
2
/
0
,
1
25
,
0
100
cm
kgf
a
de
m
P






Perda de carga: Fórmula de Darcy:
g
v
D
L
f
lw
2
2
 expresso em m
g
D
fLv
P
2
144
2


 ρ expresso em lb/ft3
expresso em lb/ft2

10. Ex. Bombear 8m3/h de um fluido com as seguintes características:
Massa específica (ρ = 850kg/m3) e viscosidade μ = 40cp.
Vel. Econômica DT =15,52 x 8 0,434 = 38,2mm
Tubo de 1 ½”, Sch 40 .......... D = 40,89 mm, área = 0,001314 m2
Checando a velocidade :
v = Q/A ............ 8 / 3600 x 0,001314 = 1,7 m/s
Calculando Re ....

vD
= 1477 ... < 2100 4f = 64/ Re = 0,0435 2f = 0.02175
Cálculo da perda de carga
( lw = (2f L v2) / (gc D) = (0.02175 x 100 x 1,72) / (9.8 x 0.04089) = 15,68 m
ΔP/ρ = - lw ..... ΔP= 850Kg/m3 x 15,68 m = 13333/10000 = 1,33 kgf/cm2
> 1 kgf/cm2…logo 1 1/2 é pequeno, usar próximo diâmetro 2”.

11. Determinando f
Re < 2100
Re
64
4 
f
Zona de transição
2
Re
log
42
,
1
4









D
f

D

560
Re 
25
,
0
Re
100
46
,
1
1
,
0
4 







D
f

D

560
Re  2
7
,
3
log
2
1
4









D
f


12. 12 m3/h de acetona 96% deverão escoar do trocador de calor de resfriamento de uma
destilaria para o tanque de armazenamento distante a 120m. Dimensionar a linha para este
serviço e especificar o material de construção. Dados T= 40º C ,μ=0,9cp, ρ=817kg/m3
Resp. inox 304, soldado (inflamável)
Veconômica 1,5 a 3,5 m/s μ baixa
Chutando 2,0 m/s + 70 % por se tratar de inox .............1,7 x 2,0 = 3,4 m/s
V =Q/A .... A= 12 / (3,4 . 3600) = 9,8.10-4 m2........1 ¼”, obs. Não é comercial,
Logo:
Escolho 1” ou 1 ½” Sch 40 , por exemplo
1” # 40 .... v = 12/( 0,0005572 .3600 = 6,0 m/s 1 ½”... v= 2,5 m/s

13. 2
1
6
1
.
min 1
,
3 Q
D 

 
434
.
0
52
,
15 Q
DT 

2- Querosene* deixa um tanque a 40º C e é bombeado para um tanque situado a 1600m
no pátio de estocagem de uma refinaria, com uma vazão de 18 m3/h. Dimensionar a
linha para este serviço. Dados: μ=2,0cp ρ=815kg/m3
Veconômica 1,5 a 3,5 m/s
Material: Aço carbono (tubo preto)
ASTM-A-53 s/costura, solda , Norma API
54,4 mm...2,0” (#40) ... D = 52,5mm . A= 0.002165 M2
Checando a velocidade V=18/(0,002165 . 3600).....v = 2,3 m/s
Calculando pelo diâmetro mínimo
Dmin = 3,1 . 8151,6 .181/2 = 40,2mm
Obs*. Fluidos sobre os quais tem-se freqüentemente projetos,...custo otimizado CE
setembro -1970
54,4 mm...

14. 3- Mel de 1ª deverá ser reciclado do tanque de centrifugação para o segundo cristalizador,
distante 40m na vazão de 6 m3/h a 60º C (60 Bé). Dimensionar a linha. Dados: μ=200cp
(60Bé) ≈ ρ = 910kg/m3.
Tubulação de inox 304
Veconômica 0,5 a 1,5 m/s
Arbitrando 0,8 m/s, teremos A= Q/V = 6/(0,8 .3600) = 2,083. 10-3 m2
#40 , diâmetro 2” (52,5mm) , A= 0,002165m2.
Checando ΔP
Do Ludwig, faixa econômica para fluidos viscosos ....25KPa até 100KPa / 100m ou,
0,25 a 1,0kgf/cm2.
D
g
v
L
f
lw
c
2
2 



gc .......... SI→ 1 J/kg (KPa) ; se 9,8 → m/s2
Cálculo da velocidade para o tubo com A = 0,002165m2
V=Q/A 6/(0,002165. 3600) = 0,77m/s
kgf/cm2 p/ Pa x por 98066,5
kgf/cm2 p/ N x por 9,8

15. Para cálculo ΔP, necessito conhecer o valor de 2f

Dv

Re
Obs.: 1cP = 10-3 Pa.s
Re = (910 kg/m3. 0,0525m . 0,77m/s) / (200. 10-3 Pa.s) = 184 (laminar)
→ 4f = 64/Re 2f = 32/Re 2f = 0,174
Lw = (0,174 . 100 m. (0,772 )m2/s2 ) / (1 . 0,0525m) = 196,5 J/Kg
Cálculo da ΔP resultante:

16. c
g
lw
P 


 
0
2
2








H
lw
g
P
z
g
g
g
v
c
c
c 
Equação de conservação de massa e energia
1ª parcela....velocidade constante (não variação da energia cinética) = zero
2ª variação de altura (considerando tubulação horizontal)
4ª perda de carga por atrito
5ª trabalho devido a eixo
gc =1
3ª perda de carga de pressão
ΔP= 196,5 J/kg . 910 kg/m3 = 178 KPa = 1,78kgf /cm2, que é maior que a faixa
admissível.
Recalcular para outro diâmetro.
Se o regime fosse turbulento
25
,
0
Re
100
46
,
1
1
,
0
4 








D
f

ou através do diagrama de Moody.

17. Óleo BPF deve ser bombeado de um TQ aquecido a 60º C para alimentar uma caldeira
na vazão de 8m3/h distante 60 m . Dimensionar a linha.
μ=120cp ρ=980kg/m3.
Tubo preto, solda
Velocidade econômica de 0,5 a 1,5 m/s, chutando 0,8 m/s
A= Q/V 8/( 0,8 . 3600) = 2,77 .10 -3 m2
2 ½” #80 .............2,73 .10-3
#40 ............. 3,09 .10-3.............D=0,06271
Checando ΔP
V= 8 / 0,00309 .3600 = 0,72 Re =

 vD

Re = 368 , laminar
4f Moody 2f = 0,087
lw = ( 0,087 . 100 . 0,722 .) / (1 . 0,06271)
ΔP= 71,91 . 980 = 70,5 KPa

18. Assumindo fluxo adiabático
Neste caso, considerando que os dutos são curtos e isolados termicamente. Isto é,
nenhum calor é transferido para, ou absorvido pelo fluido, exceto pequena quantidade
de calor gerada pela fricção devido ao fluxo.
 Considerando fluxo isotérmico:
Assumido freqüentemente por conveniência. Visto que esta condição mais se aproxima
das situações práticas de transferência de fluidos gasoso pressurizados normalmente
encontrados na indústria.
Limites de operação para cálculo com emprego da fórmula de Darcy:
Com relação a variação da densidade assumida para o fluido
 Se maior que 40% (condições freqüentemente encontradas na indústria
(tubulações de grande extensão) adotar-se as formulas que segue adiante.
FLUIDOS COMPRESSÍVEIS
Considerações inicias
 ΔP ( P1 - P2) * < 10% , boa precisão; seja usando valor médio do volume
específico, ou mesmo um ou outro valor.
 Se entre 10 a 40 %** ; recomenda-se usar volume específico médio.
cst
V
p k
n 
,
cst
V
p n 
,

19. Velocidade econômica adotada para gases de 20 a 60 m/s
Perda de carga econômica no máximo 0,5kgf/100m
Escoamento completamente isotérmico
Para facilidade de cálculo, despreza-se a variação da temperatura (regime isotérmico)
de um fluido gasoso compressível através de um duto, a custa da pequena variação de
pressão, visto a reduzida troca de calor com as paredes.
vA
w 

Se as seções são iguais teremos:
2
1 W
W 
(1) , como
Temos que,




 f
v (com Aconst.)
2
1
1
2
2
2
1
1
2
2
2
1
1
1
1






v
v
v
v
A
v
A
v
W 






20. i

De (1) temos que , a velocidade em um determinado ponto da tubulação de área A, com
massa específica
A
W
v
i
i


Balanço de energia
0
2
2








S
g
c
c
nW
lw
P
Z
g
g
g
v

Derivando o primeiro e terceiro termo e substituindo o termo lw teremos:
0
2
2
2
2



D
g
fLdv
dP
g
dv
c
c 
Elevando (2) ao quadrado e substituindo em (3), procedendo posterior
substituição em (4) e integrando teremos:
2
2
2
2
2
2
2
A
W
v


(2)
(3)
(4)







 



1
2
2
2
1
2
1
2
2
ln
2
4
.
.
P
P
P
P
P
D
fL
A
g
W
 (4)

21. 






 


1
2
2
2
1
_
1
2
2 .
.
144
P
P
P
fL
V
DA
g
W
Além da consideração de fluido completamente isotérmico também é assumido por
conveniência:
Ausência de trabalho mecânico
Fluxo invariável com o tempo
Fluido obedece as leis dos gases perfeitos
Velocidade representada pela velocidade média através da seção
f constante ao longo da tubulação
Tubulação horizontal e reta
Equação simplificada: (tubulações curtas) , ou longas, se perda de carga pequena.
- ft3/lb,
A- ft2,
P - psig,
g - 32,2 ft/s,
D- ft.
_
1
V
L - pol,
(5)

22. Outras fórmulas adotadas para dimensionamento de tubulações para fluido compressível:
 Fórmula de Weymouth:
Adotada também para ar comprimido, e gases combustíveis (S Telles, p. 237)
 
  .
520
.
0
,
28 2
2
2
2
1
667
,
2
/
,
3















 

T
L
S
P
P
d
q
m
g
h
ft
h
Lm = milhas,
d = pol,
Sg =dens. relativa
T = oR = o F + 459,67 ,
P psia
 Fórmula de Panhandle:
Para gás natural.
Aplicada à tubos de 6 até 24”, Re de 5x106 a 14x106, Sg= 0,6
5394
,
0
2
2
2
1
6182
,
2
,
.
.
8
,
36 




 

m
h
L
P
P
d
E
q E , coeficiente experimental
0,92 ( 0,85 a 0,95)
,
h
q = ft3/h – ( condição padrão- 14,7 psi 60º F),
Obs.: Diferença entre as fórmulas decorre a custa do valor de adotado
f
Diagrama de Moody: é mais frequentemente empregado.
(6)
(7)

23. 3
1
032
,
0
d
f 
Obs. Apresenta valor idêntico ao Moody para diâmetro na região de diâmetro de 20”,
maior para diâmetros menores e menores para diâmetros maiores.
 Fator de fricção por Weymouth:
(8)

24.  Fator de fricção por Panhandle:
1461
,
0
'
1225
,
0









g
hS
q
d
f
d = pol
= ft3/h (padrão)
Sg = d rel.
.
Obs. 1) Valores menores que Moody em toda extensão.
2) O uso dos fatores de fricção Weymouth ou Panhandle na fórmula geral
simplificada leva a resultados similares.
( 9)
'
h
q

25. Varias são as formas de resolução para cálculo do diâmetro de tubulações envolvendo
fluidos comprimidos.
Por exemplo:
Atribui-se um diâmetro para ficar dentro da velocidade econômica.
 Determina-se a perda de carga resultante. Atende? Ok,
 Se não atende, atribui-se outro diâmetro.
Ou ainda,
Atribui-se uma perda de carga através de P2 e calcula-se o diâmetro resultante.
 Atende a vazão mássica? Sim ? então Ok,
 Se Não atende, refaz-se o cálculo assumindo outra perda de carga.
Obs. As relações de engenharia empregam critérios de perda de carga admissível em
função de um comprimento unitário de tubulação. Na prática, no sistema inglês adota-se
perda de carga por 100 ft. Ainda , os valores assumidos levam em consideração a pressão
de operação da linha

26. Equação que representa o fator de fricção na região turbulenta (tubo liso) no diagrama .
de Moody
16
,
0
0185
,
0 










Dv
f
Ainda, obtido de dados práticos obtem-se uma relação que expressa o quociente ΔP/L
D
v
f
ft
P 2
518
,
0
100



(11)
(12)
Substituindo – se da equação 11 na equação 12 e explicitando - se D tem-se
uma equação que determina o diâmetro como função da referida perda de carga.
f
207
,
0
84
,
1
16
,
0
100
706
,
1

















 

P
W
D

 (13)
D pol
W lb/h
ρ lb/ft3
μ cP
P psia

27. Exemplo de Gráfico relacionando a (perda de carga /100ft ) versus
(pressão do sistema)
Do artigo: Kent, G. R. Chemical Engineering, September, 25, 1976
Pressão (psia)
P/ (gases) - pressão do sistema, P (psia),
P/líquidos – quociente da pressão do sistema / pressão de vapor
v
p
p

28. Escolhida três regiões da curva, (ΔP/100ft) versus (P1) para gases teremos após a
conversão para o SI:
1- P1 < 6,3 kgf/cm2 6379
,
0
1
.
05
,
0
100
P
m
P


2- 6,3 Kgf/cm2 < P1 < 14 Kgf/cm2 363
,
0
1
.
082
,
0
100
P
m
P


3- 14 Kgf/cm2 < P1 < 70 Kgf/cm2 157
,
0
1
144
,
0
100
P
m
P


Obs. Para valores de pressão acima de 1000psia
12
,
0
49
,
0
100



ft
P
Gases → Para P > 1000,
Líquidos → Para
v
p
p*
> 1000,
042
.
0
5
,
1
100 









v
P
P
ft
P
P* , pressão do sistema

29. DETERMINAÇÃO DA VELOCIDADE EM DUTOS DE DIÂMETRO CONHECIDO
formulas típicas
Para líquidos )
/
(
6
,
5 304
,
0
s
ft
D
v  D diâmetro típico
Para gases )
/
(
6
,
43 16
,
0
45
,
0
s
ft
D
v

 D (polegada), ρ (lb/ft3)
DETERMINAÇÃO DA VELOCIDADE LIMITE
Obs. A velocidade média para gases pode ser aproximada
para 2/3 da velocidade máxima.
T = oR
m = Mol
k = Cp/Cv
Z compressibilidade
2
/
1
7
,
148 






m
kZT
v s
ft/
3
/
1
48


v s
ft/
(líquidos limpos)
(gases limpos):

30. Velocidades
Gases
Superaquecidos de 15 a 60 m/s
Saturados de 15 a 35 m/s, ar de 8 a 10 m/s.

31. f
16
,
0
0185
,
0 










Dv
f
DETERMINAÇÃO DO COEFICIENTE DE FRICÇÃO
Na ausência do diagrama de Moody a fórmula
de regime turbulento para tubos limpos de aço.
possibilita determinar o fator de fricção na região

32. Exercício:
Determinar o diâmetro de uma tubulação para transporte 600Nm3/min. de butano que se
encontra a 450º K e a pressão de 10 bar (147psia)
Dados na condição de processo: μ = 4 x 10-5 Pa.s , = 0,0502 m3/kg
Usando critério de perda de carga.
Do gráfico de ΔP/100ft para gases temos para 147 psia: ≈ 0.8 psi/100ft
Convertendo as unidades PSI → Pa lbf /in2.............N/m2 ..................1bar = 105 Pa
lbf para N x 4,448 1 bar= 105 Pa
in2 para m2 x 0,000645
4,448/0,000645 = 6896, logo ΔP= 0,8 x 6896 = 5516 Pa
0.8 psi / 100 ft, isto é: 0,8 psi para cada 100 pés ou 5516 Pa para cada 30,48 m,
Logo, se P1 for 10 bar ( 10 x105 Pa), P2 será 10 x105 – 5516 = 9,9448 x105 Pa
Nas condições normais a massa específica é:
3
46
,
2
288
082
,
0
12
,
58
1
m
kg
x
x
RT
PM




(1 atm, 15º C)
_
V
_
V

33. Vazão mássica:
ρ nas condições da linha: ρ = 1/,0502 = 19,92
Adotando velocidade econômica para gases 30m/s.
De vA
W 

Área para o tubo:
2
10
11
,
4
30
0502
,
0
1
6
,
24
30
1
6
,
24 




 x
x
x
A
v
W
A


(tubo de 1 0 “ #40 ... A= 0,05324 Diâmetro de 273 mm
Aplicando os dados na equação →







 



1
2
1
2
1
2
1
2
2
ln
2
4
.
.
P
P
P
P
P
D
fL
A
g
W

f

dv

Re
Para determinação de
Obs, ρ nas condições da linha.
s
kg
s
x
Q
W 6
,
24
60
600
46
,
2


 
Kg /m3

34. Re = 19,92 x 0,0422 x 30 / 0,04 = 630 laminar
  







 


 6
2
12
6
2
2
10
994484
10
994484
10
1
ln
2
273
,
0
48
,
30
025
,
0
4
000966
,
0
8
,
9
92
,
19
x
x
x
x
x
W
.
Verificar valor encontrado para a vazão. Se não atender, trabalho com outro diâmetro.
Através de processo iterativo chego ao diâmetro que melhor atende a perda de carga
admissível.
Obs. Se ΔP < 0,1 P1 posso assumir ρ = ρ1 = ρ2
Do diagrama de Moody
4 f = 64/Re f = 0,025
Se 0,1 P1 < ΔP < 0,4 P2
2
2
1 





35. Ex. 2 Calcular o diâmetro necessário para uma tubulação (80m), contendo 2 válvulas
globo (Leq = 340D) que passará 30Nm3/min. de etileno a 20kgf/cm2 abs, na temperatura
de 35º C
μ= 0,011 cP e volume específico = 0,086m3/h . Tc etileno 282K...
Usando critério 3, obtido do gráfico
14 Kgf/cm2 < P1 < 70 Kgf/cm2 157
,
0
1
144
,
0
100
P
m
P


2
151
,
0
22
,
0
20
144
,
0
100
cm
kgf
x
m
P



lw =
3
18
,
1
288
082
,
0
28
1
m
kg
x
x
RT
PM



 Vazão mássica s
kg
s
x
Q
W 59
,
0
60
30
18
,
1


 
_
V

36. Observações quanto a limites de velocidade para um fluido compressível.
A velocidade máxima de um fluido compressível está limitada à velocidade de
propagação da onda de pressão que viaja na velocidade do som naquele fluido. A
pressão cai à jusante, na medida em que o fluido percorre o duto. Em conseqüência a
velocidade aumenta atingindo no máximo a velocidade de propagação do som
naquele meio. Ainda que a pressão caia demasiadamente na saída, esta não será
sentida a montante, pois a onda de pressão viaja com menor velocidade que o som.
Em conseqüência, qualquer possível redução adicional de pressão na saída, após a
máxima vazão ter sido alcançada ( condição de velocidade sônica), este efeito só se
manifestará após a saída da tubulação. A energia a custa da conversão do incremento
de pressão dará origem a uma onda de choque e turbulência no jato de fluido
expelido.

37. Velocidade máxima possível para um fluido no interior de um duto (velocidade sônica*)
_
144 V
P
g
gRT
vs 
 

v
p
C
C


Obs.* A máxima velocidade de um fluido compressível em um tubo é limitada pela
velocidade de propagação da onda de pressão, que viaja na velocidade do som no fluido.
Então, se a perda de carga é suficientemente alta, a velocidade de saída pode alcançar , no
máximo, a velocidade de propagação do som no fluido.
Esta vazão foi experimentalmente calculada para saber a quantidade de vapor que sairia
por uma tubulação se a válvula permanecesse totalmente aberta até fosse alcançado fluxo
critico.
A equação que fornece a vazão é;
g
h
S
T
K
P
P
d
Y
q








1
1
2
31
,
19
onde : h
q = vazão volumétrica em m3/h
Y = fator de expansão para fluidos
compressíveis (de Crane A-22)
, para 3
,
1


v
p
c
c


38. = diferença de pressão entre a entrada e a saída da tubulação
Considerando os valores de e
K
1
P
P

= diâmetro da tubulação.
d
P

1
P = pressão na entrada (bar)
1
T = temperatura na entrada em K (grau Kelvin)
g
S = densidade relativa do gás em relação ao ar
Observar que o valor de ( coeficiente de resistência) na situação tratada refere-
se a regime turbulento
K
≈ 1,4 para ar e gases diatômicos,
≈1,66 para monoatômicos e
≈1,33 p/tri atômicos.
Cv para o ar e gases diatômicos = 0,0639 kcal/kg
Cp = 0,1321
Obs.O coeficiente isentrópico k, para o vapor varia de 1,33 a 1,25 (de 1 a 2000
psi) correspondendo a uma faixa de temperatura de (300F a 1400F).


39.  
1
_
2
.
525
,
0
/
V
K
P
Yd
s
lb
w


EQUAÇÃO DE DARCY
INCLUINDO O COEFICIENTE DE EXPANSÃO “Y” PARA FLUXO ADIABÁTICO.
Observação quanto à perda de carga:
 Fricção: a custa de rugosidade da parede, em conseqüência do diâmetro, densidade,
e viscosidade.
 Mudanças de direção
 Obstrução (constricção)
 Brusca ou gradual variação na seção transversal e forma do caminho de fluxo
 ∆P para descarga de fluido compressível para atmosfera representa a diferença entre
o valor de P1(absoluta) e a atmosférica.
 No cálculo, determinação dos dados de tabela para determinação do coeficiente Y,
aplicado a relação ΔP/P1, mede-se a diferença entre as pressão de entrada e a pressão
na seção de maior velocidade.
 Y - relacionado à mudança nas propriedades do fluido – fator de expansão







D
L
f
K
K, coeficiente de resistência
Onde,
∆P = a ≠ P1 entrada menos a P na área expandida, ou atmosférica

40. Apêndice
*Se ∆P < 10 % pode-se empregar com erro desprezível a equação de Darcy
Equação de Darcy
g
D
fLv
P
2
144
2



D
g
fLv
P
c
2
2


g
v
D
L
f
hL
2
2


Ou ainda,
g
v
K
hL
2
2

D
L
f
K 

41. **Se ∆P entre 10 e 40% pode-se empregar também a equação
Esta equação também se emprega para determinar vazão através de
região onde ocorre expansão.
Obs. Se ∆P ˃ 40% foge aos limites da equação de Darcy
Apêndice
lb/s
2 _
2
525
,
0
V
K
P
Yd
w



coeficiente de resistência (válvulas, curvas, bocais, etc..tabela 1-4)

w

Y Fator de compressibilidade
K
v
P
c
c

K Obs. Não confundir com k (minúsculo)

42. k≈1,3 aplicável para CO2, SO2, H2O, H2S, NH3, N2O, Cl2, CH4, C2H2 e C2H4

43. k≈1,4 aplicável para Ar, CO, O2, H2, N2, NO, HCl

44. Exemplo
Uma tubulação com vapor saturado a 170 psia é acoplada à um vaso de cozimento que opera a
pressão atmosférica. Sabendo-se que esta tubulação é constituída de duas curva de 90 graus e uma
válvula globo e que a tubulação tem 2,0 pol. de diâmetro (#40), com 30 pés de comprimento,
pergunta-se. Qual a vazão de alimentação do vaso sabendo-se que o bocal de tem a mesma seção da
tubulação? Ver croquis
 
1
_
2
525
,
0
/
V
K
P
Yd
s
lb
w


Determinando os comprimentos equivalentes
Da eq. de Darcy,
Para o tubo (30 x 12 x 0,019) / (52,5/25,4) = 3,309
Para a válvula globo 340 x 0,019 = 6,46
Para o bocal de entrada K = 0, 04
Para bocal de saída K = 1,0
Para curva 90 graus (duas) 2 x 30 x 0,019 = 1,14
Ktotal = 3,309 +6,46 + 0,04 + 1,0 + 1,14 = 11,95
D
L
f
K 
T
f
340
T
f
30

45. 914
.
0
170
7
,
14
170
,
1




P
P
Para K = 11,95, interpolando entre
valores de K = 10 e K = 15,
Teremos para = 0,785,
Sendo o valor limite atingível, bem
menor que 0,914.
Teremos na saída da tubulação condição
de velocidade sônica.
,
1
P
P

5
,
133
170
785
,
0 


P
Com o valor 0,785, por interpolação, determinamos o correspondente valor de Y que
será 0,710
Teremos então
Com o valor máximo 0,785 calculamos a perda de carga limite
s
lb
w /
25
,
3
6738
,
2
95
,
11
5
,
133
272
,
4
710
,
0
525
,
0 





6738
,
2
170 
V
Tubo 2” #40
diametro interno= 2,067”

47. Estado físico Meios Velocidade
aproximada
Sólidos Aço
Granito
Pirex
5790 m/s
6000
5640
Líquidos Água
Água do mar
Mercúrio
1482
1522
1450
gases Hidrogênio
Ar
Hélio
965
343
331
Velocidade aproximada de propagação do som em
alguns diferentes meios (valores a 20ºC)

48. Valores de (k = Cp/Cv) para algumas substâncias gasosas
acetileno 1,30 hidrogênio 1,41
ar 1,40 sulfeto de hidrogênio 1,30
amônia 1,32 metano 1,32
argônio 1,67 cloreto de metila 1,20
butano 1,11 gás natural 1,27
dióxido de carbono 1,30 óxido nítrico 1,40
monóxido de carbono 1,40 nitrogênio 1,41
cloro 1,33 óxido nitroso 1,31
etano 1,22 oxigênio 1,40
etileno 1,22 propano 1,15
helio 1,66 propeno 1,14
cloreto de hidrogênio 1,41 óxido de enxofre 1,26