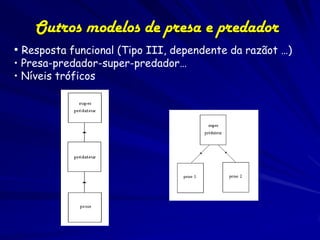
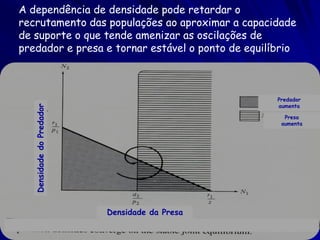
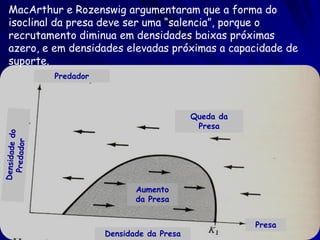
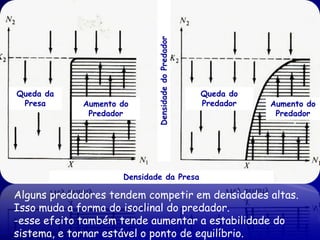
1) O documento discute três modelos matemáticos de interação entre predadores e presas: o modelo de Lotka-Volterra, o modelo de Nicholson-Bailey, e o modelo de Rosenzweig-MacArthur. 2) O modelo de Nicholson-Bailey considera a mortalidade do parasitóide independente da densidade e o atraso na conversão de energia em nascimentos. 3) O modelo de Rosenzweig-MacArthur modifica a taxa de crescimento da presa em baixas e altas densidades e inclui dependência da densidade para o predador.

1. Outros Modelos de predador e
presa
Prof. Dr. Harold Gordon Fowler
popecologia@hotmail.com
Ecologia de Populações

2. Modelos da Predação
A. J. Lotka (1925) e A. Volterra (1926)
independentemente derivaram um modelo similar
que modifica a equação logística para lidar com duas
espécies- um predador e uma presa.
Outras modelos existem.
3 Modelos:
1. Lotka e Volterra
2. Nicholson e Bailey
3. Rosenweig e Mac Arthur

3. Modelo de Nicholson e Bailey
Nicholson e Bailey desenvolveram um modelo de
Hospedeiro e Parasitóide com premissas mais
atuais:
- a mortalidade do parasitóide é independente
da densidade.
- conversão da energia por predadores em
nascimentos é retarda por uma geração.

4. Modelo de Nicholson e Bailey
Equação do crescimento do hospedeiro:
H t+1 = r H t e (-a Pt)
Equação de crescimento do parasitóide:
P t+1 = Pt [ 1 - e (-a Pt) ]
Onde H é o hospedeiro. P é o parasitóide.
t é o tempo, r é a taxa finita de aumento do hospedeiro.
a é a taxa de parasitismo para cada parasitóide

5. Modelo de Nicholson e Bailey
Equação do crescimento do hospedeiro:
H t+1 = r H t e (-a Pt)
Equação de crescimento do parasitóide:
P t+1 = Pt [ 1 - e (-a Pt) ]
Se o número de hospedeiros retirados pelos parasitóides é
igual a fração dos hospedeiros que é o recrutamento,
então não há mudanças populacionais.
Se o parasitóide retira parte dos hospedeiros então a
população do parasitóide diminua.
Assim, a sobre-exploração pelo parasitóide pode resultar em
oscilações maiores e a extinção possível de uma das
populações.

6. Modelo de Rosenzweig e MacArthur
Rosenweig e MacArthur também desenvolveram um
modelo de predador e presa.
Esse modelo modifica o isoclinal de “crescimento
zero” da presa para lidar com uma taxa baixa de
crescimento a densidades altas e baixas.
Também, o crescimento do predador estabelece a
densidades altas (dependência da densidade, ou o
modelo logístico).
Neste modelo, o equilíbrio do predador e da presa
aumenta e cai com a produtividade da presa (mais
real).

7. Modelo de Rosenzweig e MacArthur
dN  N  aN
 rN1  P
dt  K  1 wN
dP  aN 
 P
c  g
dt  1 wN 

8. A dependência de densidade pode retardar o
recrutamento das populações ao aproximar a capacidade
de suporte o que tende amenizar as oscilações de
predador e presa e tornar estável o ponto de equilíbrio
Predador
aumenta
Densidade do Predador
Presa
aumenta
Densidade da Presa

9. MacArthur e Rozenswig argumentaram que a forma do
isoclinal da presa deve ser uma “salencia”, porque o
recrutamento diminua em densidades baixas próximas
azero, e em densidades elevadas próximas a capacidade de
suporte.
Predador
Queda da
Presa
Aumento
da Presa
Presa
Densidade da Presa

10. Densidade do Predador
Queda da Queda do
Presa Aumento do Predador Aumento do
Predador Predador
Densidade da Presa
Alguns predadores tendem competir em densidades altas.
Isso muda a forma do isoclinal do predador.
-esse efeito também tende aumentar a estabilidade do
sistema, e tornar estável o ponto de equilíbrio.

11. A eficiência do
predador pode ter
efeitos grandes num
sistema de predador e
presa
predadores menos
eficientes somente
Densidade do Predador
podem reproduzir
quando sua presa
Densidade aproxima a capacidade
de suporte.
Mais estabilidade
predadores muito
eficientes podem forçar
a presa a extinção e
assim também tornam
extintos.
Menos estabilidade

12. Outros modelos de presa e predador
• Resposta funcional (Tipo III, dependente da razãot …)
• Presa-predador-super-predador…
• Níveis tróficos

13. Condições de estabilidade de Routh e
Hurwitz
• Equações características
n  a1n1  a2n2  ...  an1n1  an  0
• Condições de estabilidade : M* l.a.s.
k , R(k )  0  H i  0
a1 a3 a5
a1 a3
H 1  a1 H2  H3  1 a2 a4
1 a2
0 a1 a3

14. Condições de estabilidade de Routh e
Hurwitz
• Dimensão 2
2  trA  det A  0
H1  a1  trA  0
H 2  a1a2  a3  det A  0
• Dimensão 3
3  a12  a2  a3  0
H1  a1  0
H 2  a1a2  a3  0
H 3  a3  0

15. Exemplo de 3 níveis tróficos
dx
 rx  axy
dt
dy
  my  bxy  cyz
dt
dz
 z (1  z )  dyz
dt

16. Seleção de um modelo
Lotka e Volterra Clássico
(crescimento exponencial da presa, resposta funcional Tipo
I do predador)
Não estável estruturalmente, mas interesse histórica
Lotka e Volterra
(crescimento logístico da presa, resposta funcional Tipo I
do predador)
Não tem ciclos!
Rosenzweig-MacArthur
(crescimento logístico da presa, resposta funcional Tipo II
do predador, saciação do predador)
Ciclos!