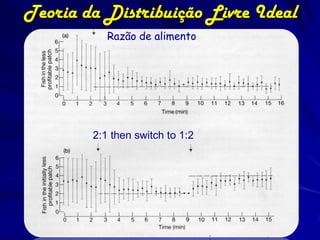
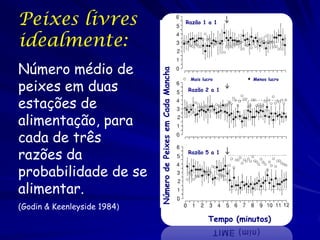
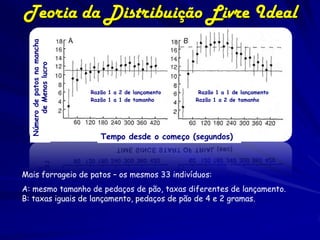
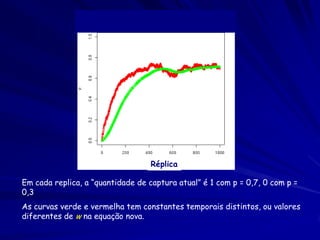
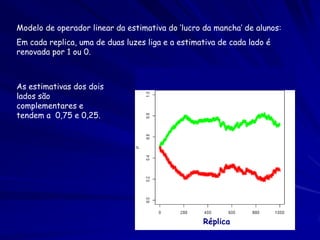
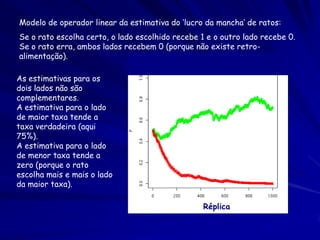
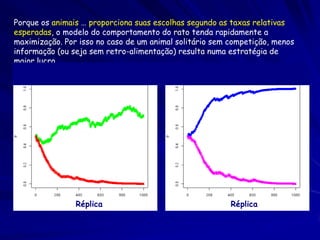
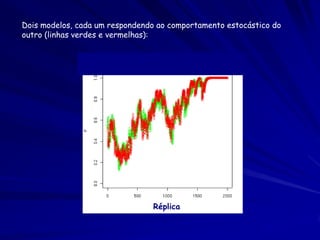
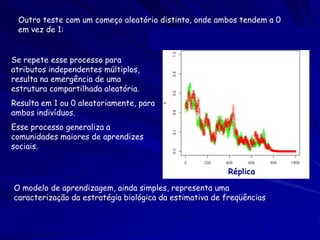
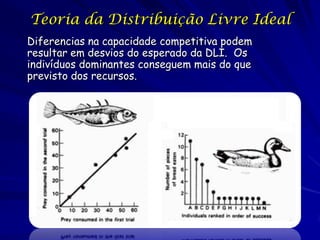
O documento discute a Teoria da Distribuição Livre Ideal, que afirma que animais se distribuem espacialmente de forma a igualar sua taxa de obtenção de recursos. Estudos com peixes e patos mostraram que eles se distribuem de acordo com a teoria quando a competição e disponibilidade de recursos são variáveis. No entanto, diferenças competitivas entre indivíduos podem levar a desvios da previsão da teoria.

1. Prof. Dr. Harold Gordon Fowler
popeclogia@hotmail.com
Ecologia de Populações
Teoria da Distribuição
Livre Ideal

2. Teoria da Distribuição
Livre Ideal
No forrageio as escolhas se dividem
estocasticamente segundo uma estimativa da
“lucro da mancha”
Estratégia evolutivamente estável
– Sob a competição para recursos heterogêneos
– Mas animais isolados também usam essa estratégia
Re-interpretação de muitos paradigmas de
aprendizagem e condicionamento
– Uma estimativa do “lucro da mancha” combinada
com a alocação estocástica de escolhas de forma
proporcional
– Um estimador linear simples ajusta a maior parte
dos dados

3. Teoria da Distribuição Livre Ideal
Distribuição espacial dos recursos
A Distribuição Livre Ideal (DLI)
-- ONDE forragear depende do número de
presas e a competição entre forrageiras.
-- A DLI afirma que os animais se dispersam para
igualar sua entrada de energia ou sucesso
reprodutivo
Milinski, M. 1979. An evolutionarily
stable feeding strategy in
sticklebacks. Zeitschrift fur
Tierpsychologie 51:36-40.
Colocou 6peixes num tanque e os
alimentou a taxas diferentes aos
extremos do tanque.

4. Forrageio Livre Ideal
Peixes distribuídos
num tanque de
forma que a
entrada média de
energia é igual
entre os
indivíduos

5. Teoria da Distribuição
Livre Ideal
No forrageio as escolhas se dividem
estocasticamente segundo uma estimativa da
“lucro da mancha”
Estratégia evolutivamente estável
– Sob a competição para recursos heterogêneos
– Mas animais isolados também usam essa estratégia
Re-interpretação de muitos paradigmas de
aprendizagem e condicionamento
– Uma estimativa do “lucro da mancha” combinada
com a alocação estocástica de escolhas de forma
proporcional
– Um estimador linear simples ajusta a maior parte
dos dados

6. Teoria da Distribuição Livre Ideal
Razão de alimento
2:1 then switch to 1:2

7. Peixes livres Razão 1 a 1
idealmente:
Número médio de
Número de Peixes em Cada Mancha
peixes em duas
Mais lucro Menos lucro
Razão 2 a 1
estações de
alimentação, para
cada de três
razões da Razão 5 a 1
probabilidade de se
alimentar.
(Godin & Keenleyside 1984)
Tempo (minutos)

8. Teoria da Distribuição Livre Ideal
Distribuição espacial dos recursos
A Distribuição Livre Ideal (DLI)
-- os peixes são “expertos” e
conformam a DLI. Outros estudos
demonstram resultados similares.
Harper DC, 1982. Competitive foraging in mallards:
“ideal free” ducks. Anim Behav 30:575-84
Mas, a DLI não sempre funciona.
Por que?

9. Teoria da Distribuição Livre Ideal
Número de patos na mancha
de Menos lucro
Razão 1 a 1 Razão 1 a 2
Tempo desde o começo (segundos)
Patos livres idealmente: banda de 33 patos com dois homens lançando
pedaços de pão.
A: ambos lançam a cada 5 segundos.
B: um lança a cada 5 segundos, e o outro lança a cada 10 segundos.
(Harper 1982)

10. Teoria da Distribuição Livre Ideal
Número de patos na mancha
de Menos lucro
Razão 1 a 2 de lançamento Razão 1 a 1 de lançamento
Razão 1 a 1 de tamanho Razão 1 a 2 de tamanho
Tempo desde o começo (segundos)
Mais forrageio de patos – os mesmos 33 indivíduos:
A: mesmo tamanho de pedaços de pão, taxas diferentes de lançamento.
B: taxas iguais de lançamento, pedaços de pão de 4 e 2 gramas.

11. Modelo de Operador Linear
O animal fica com uma estimativa da densidade de
recursos para cada mancha (ou freqüência de resposta)
As vezes se renova a estimativa
A nova estimativa é uma combinação da estimativa
anterior e a “quantidade de captura atual”
Agora: En  wEn1  (1  w)C
W = “constante da memória”
C = “quantidade da captura atual”
Bush e Mosteller (1951), Lea e Dow (1984)

12. O que é E?
Em modelos diferentes:
– Estimativa da densidade de recursos
– Estimativa da freqüência de eventos
– Probabilidade da resposta
– Força da associação
– ???

13. Réplica
Em cada replica, a “quantidade de captura atual” é 1 com p = 0,7, 0 com p =
0,3
As curvas verde e vermelha tem constantes temporais distintos, ou valores
diferentes de w na equação nova.

14. Modelo de operador linear da estimativa do ‘lucro da mancha’ de alunos:
Em cada replica, uma de duas luzes liga e a estimativa de cada lado é
renovada por 1 ou 0.
As estimativas dos dois
lados são
complementares e
tendem a 0,75 e 0,25.
Réplica

15. Modelo de operador linear da estimativa do ‘lucro da mancha’ de ratos:
Se o rato escolha certo, o lado escolhido recebe 1 e o outro lado recebe 0.
Se o rato erra, ambos lados recebem 0 (porque não existe retro-
alimentação).
As estimativas para os
dois lados não são
complementares.
A estimativa para o lado
de maior taxa tende a
taxa verdadeira (aqui
75%).
A estimativa para o lado
de menor taxa tende a
zero (porque o rato
escolha mais e mais o lado
da maior taxa).
Réplica

16. Porque os animais … proporciona suas escolhas segundo as taxas relativas
esperadas, o modelo do comportamento do rato tenda rapidamente a
maximização. Por isso no caso de um animal solitário sem competição, menos
informação (ou seja sem retro-alimentação) resulta numa estratégia de
maior lucro.
Réplica Réplica

17. O comportamento do rato influencia a evidencia que ele percebe.
Essa retro-alimentação determina sua estimativa da probabilidade de se
alimentar no ramo da taxa menor e tende a zero.
Se aplicamos esse modelo a uma decisão de duas escolhas na qual a evidencia
sobre ambas escolhas está influenciada pelo comportamento do aprendiz –
como no caso onde dois operadores aprendizes lineares estão estimando o
comportamento do outro – então o mesmo efeito de retro-alimentação
resultará numa estimativa de uma escolha a 1 e a outra a 0.
Porém, a escolha é aleatória e tende a zero.

18. Dois modelos, cada um respondendo ao comportamento estocástico do
outro (linhas verdes e vermelhas):
Réplica

19. Outro teste com um começo aleatório distinto, onde ambos tendem a 0
em vez de 1:
Se repete esse processo para
atributos independentes múltiplos,
resulta na emergência de uma
estrutura compartilhada aleatória.
Resulta em 1 ou 0 aleatoriamente, para
ambos indivíduos.
Esse processo generaliza a
comunidades maiores de aprendizes
sociais.
Réplica
O modelo de aprendizagem, ainda simples, representa uma
caracterização da estratégia biológica da estimativa de freqüências

20. Teoria da Distribuição Livre Ideal
Diferencias na capacidade competitiva podem
resultar em desvios do esperado da DLI. Os
indivíduos dominantes conseguem mais do que
previsto dos recursos.