O documento resume os principais conceitos sobre números complexos, incluindo:
1) Sua representação algébrica como a + bi, onde a é a parte real e bi é a parte imaginária;
2) O número imaginário i, com a propriedade i2 = -1;
3) As operações básicas de soma, subtração, multiplicação e divisão de números complexos nas formas algébrica e trigonométrica.











![Exemplo:
(PUC-MG) O número complexo (1 + i) 10 é
igual a:
a) 32 b) -32 c) 32i d) -32i e) 32(1+i)
[(1 + i)2]5 = [1 + 2i + i2]5 = [1 + 2i - 1]5 =
[2i]5 = 32.i5 = 32i letra C](https://image.slidesharecdn.com/nmeroscomplexos-130306120543-phpapp01/85/www-videoaulagratisapoio-com-br-Matematica-Numeros-Complexos-12-320.jpg)










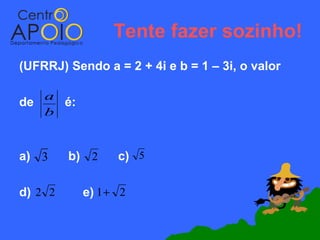









![Como multiplicamos
complexos na forma
trigonométrica?
z1.z 2 = ρ1.ρ 2 .[ cos(θ1 + θ 2 ) + isen(θ1 + θ 2 ) ]
Exemplo:
π π π π
z1 = 2 cos + isen e z2 = 3 cos + isen
3 3 2 2
π π π π
z1.z 2 = 2.3cos + + isen +
3 2 3 2
5π 5π
z1.z 2 = 6 cos + isen
6 6 ](https://image.slidesharecdn.com/nmeroscomplexos-130306120543-phpapp01/85/www-videoaulagratisapoio-com-br-Matematica-Numeros-Complexos-33-320.jpg)
![Como dividimos
complexos na forma
trigonométrica?
z1 ρ1
= [ cos(θ1 − θ 2 ) + isen(θ1 − θ 2 ) ]
z2 ρ 2
Exemplo:
π π π π
z1 = 6 cos + isen e z 2 = 3 cos + isen
2 2 3 3
z1 6 π π π π
= cos − + isen −
z2 3 2 3 2 3
z1 π π
= 2 cos + isen
z2 6 6](https://image.slidesharecdn.com/nmeroscomplexos-130306120543-phpapp01/85/www-videoaulagratisapoio-com-br-Matematica-Numeros-Complexos-34-320.jpg)
![Como calculamos uma
potência complexos na
forma trigonométrica?
z n = ρ n .[ cos( nθ ) + isen( nθ ) ]
Exemplo:
π π
z = 2 cos + isen
3 3
π π
z = 2 cos 2. + isen 2.
2 2
3 3
2π 2π
z = 4 cos
2
+ isen
3 3 ](https://image.slidesharecdn.com/nmeroscomplexos-130306120543-phpapp01/85/www-videoaulagratisapoio-com-br-Matematica-Numeros-Complexos-35-320.jpg)



![d) Escrito na forma trigonométrica
tem-se:
z = 6( cos π + i senπ )
z = ρ ( cos θ + isenθ ) = 6( cos 90º +isen90º )
e) z2 é um número real.
z n = ρ n [ cos( nθ ) + isen( nθ ) ] =
z 2 = 6 2 [ cos( 2.90º ) + isen( 2.90º ) ] =
z 2 = 36[ cos(180º ) + isen(180º ) ] =
z = 36[ − 1 + i.0] = −36
2
Resposta: letra D.](https://image.slidesharecdn.com/nmeroscomplexos-130306120543-phpapp01/85/www-videoaulagratisapoio-com-br-Matematica-Numeros-Complexos-39-320.jpg)