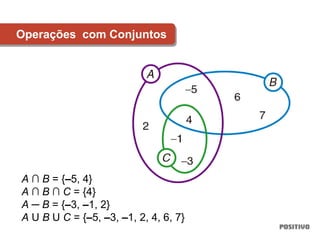
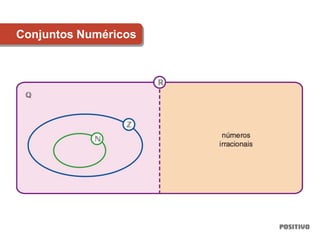
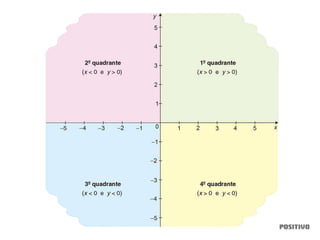
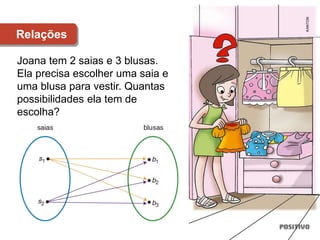
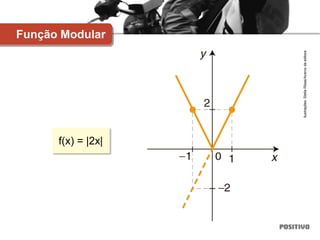
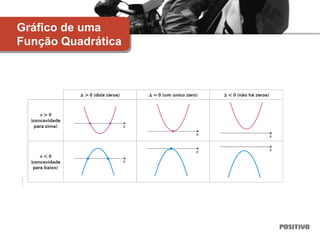
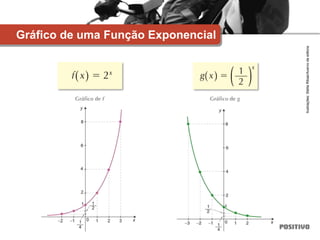
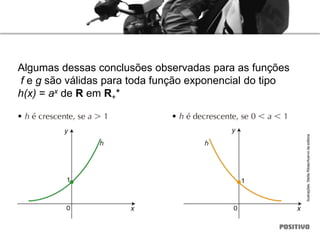
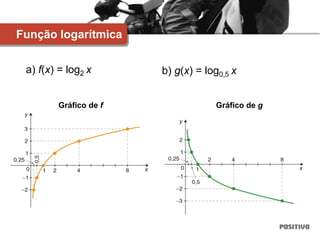
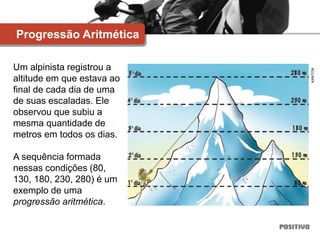
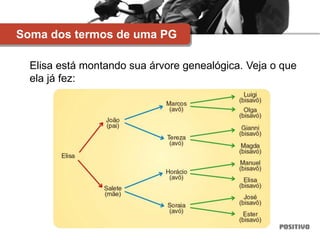
1) O documento discute conceitos matemáticos como conjuntos, funções, trigonometria e geometria. 2) Inclui exemplos de diferentes tipos de funções como funções afim, quadrática, exponencial e logarítmica. 3) Também aborda tópicos como progressões aritméticas e geométricas e razões trigonométricas no triângulo retângulo.

1. 1º ANO
MATEMÁTICA
ORGANIZAÇÃO: ÂNGELA TRINDADE
EDIÇÃO: JEFERSON FREITAS
CRÉDITOS DAS IMAGENS
DE ABERTURA:
JO RABHANSL/PATHERMEDIA/KEYDISC
© Editora Positivo Ltda., 2014

2. 1. CONJUNTOS

3. Pode-se dizer que a Região Sudeste é um conjunto de
estados e cada um dos estados que a compõem são os
elementos desse conjunto: Espírito Santo, Minas Gerais,
Rio de Janeiro e São Paulo.
Ilustração:
Stella
Ribas/Acervo
da
editora

4. A ∩ B = {–5, 4}
A ∩ B ∩ C = {4}
A ─ B = {–3, –1, 2}
A U B U C = {–5, –3, –1, 2, 4, 6, 7}
Operações com Conjuntos

5. Conjuntos Numéricos

6. Intervalos Numéricos

7. 2. ESTUDO GERAL
DE FUNÇÕES

9. Relações
KANTON
Joana tem 2 saias e 3 blusas.
Ela precisa escolher uma saia e
uma blusa para vestir. Quantas
possibilidades ela tem de
escolha?

10. A distância que um automóvel percorre é uma função do
tempo de viagem, se a velocidade for constante.
Funções
KANTON

12. 3. FUNÇÃO AFIM

13. Um turista em viagem ao arquipélago de
Fernando de Noronha decidiu mergulhar.
Antes, recebeu um treinamento prévio, no qual
foi informado de que a pressão ao nível do
mar é de 1 atm e que, a cada 10 m de
profundidade no mergulho, a pressão
aumenta de 1 atm.
A partir das orientações dadas ao turista,
podemos modelar a situação com uma função
de R+ em R+, que relaciona a pressão (y), em
atm, com a profundidade (x), em metros, cuja
lei é y = 0,1x + 1.
DORIVAL
MOREIRA/PULSAR
IMAGENS

14. Uma pessoa está parada em um
ponto de ônibus. A posição em que
ele se encontra é sempre a mesma,
até que ela entra no ônibus.
A distância percorrida por essa
pessoa em função do tempo,
enquanto ela está no ponto de
ônibus, é dada por d = 0, que é
uma função constante.
Função Constante
KANTON

15. Função Polinomial
do 1.º Grau

16. Função Modular
f(x) = |2x|
Ilustrações:
Stella
Ribas/Acervo
da
editora

17. 4.FUNÇÃO QUADRÁTICA

18. O dono de um hotel notou que, se cobrar R$ 80,00 a
diária, consegue ocupar o hotel com 100 hóspedes por
dia e, para cada R$ 5,00 a mais na diária, a ocupação
decresce de 1 hóspede.
Se a cada dia o hotel apresenta um custo fixo de
R$ 2.000,00 e um custo variável de R$ 20,00 por
hóspede, o dono do hotel pode calcular o lucro diário por
meio de L = –5n² + 440n + 4.000, que calcula o lucro em
função do número n de hóspedes que faltam para a
lotação máxima de 100 hóspedes.

19. CARSTEN
LINNENBERG/PANTHERMEDIA/KEYDISC
Certamente você já viu as pequenas antenas parabólicas colocadas
nas residências para captar os sinais de TV via satélite. Elas são
construídas, como o próprio nome indica, segundo uma parábola.

20. Gráfico de uma
Função Quadrática

21. Como o movimento da bola
é descrito por uma função
quadrática, a maior altura
que a bola consegue atingir
é denominado valor
máximo da função.
Valor máximo e
valor mínimo
Ao bater uma falta, geralmente, a bola
executa um movimento parabólico.
SEBASTIAN
SCHUBANZ/PANTHERMEDIA/KEYDISC

22. 5. FUNÇÃO
EXPONENCIAL

23. O número 9 na linguagem binária pode ser escrito como
1 0 0 1, porque 9 = 1 ∙ 2³ + 0 ∙ 2² + 0 ∙ 2 + 1 ∙ 20
Pode-se dizer então que existem 1 0 tipos de pessoas
no mundo: as que conhecem linguagem binária e as
que não conhecem!
KANTON

24. Função Exponencial

25. Gráfico de uma Função Exponencial
Ilustrações:
Stella
Ribas/Acervo
da
editora

26. Ilustrações:
Stella
Ribas/Acervo
da
editora
Algumas dessas conclusões observadas para as funções
f e g são válidas para toda função exponencial do tipo
h(x) = ax de R em R+*

27. 6. FUNÇÃO
LOGARÍTMICA

28. Logaritmos

29. Função logarítmica
Gráfico de f Gráfico de g
a) f(x) = log2 x b) g(x) = log0,5 x

30. 7. SEQUÊNCIAS

31. Qual é a figura que vem a seguir nestas sequências?
Sequências

32. Um alpinista registrou a
altitude em que estava ao
final de cada dia de uma
de suas escaladas. Ele
observou que subiu a
mesma quantidade de
metros em todos os dias.
A sequência formada
nessas condições (80,
130, 180, 230, 280) é um
exemplo de uma
progressão aritmética.
Progressão Aritmética
KANTON

33. v
Esta é a sequência de obtenção do fractal geométrico
triângulo de Sierpinski proposto no início do século XX
pelo matemático polonês Waclaw Sierpinski (1882-1969)
Progressão geométrica
Stella
Ribas/Acervo
da
editora

34. Nesta sequência, considerando os triângulos verdes,
temos 1 triângulo, 3 triângulos, 9 triângulos,
27 triângulos, etc.
A sequência (1, 3, 9, 27....) é uma progressão
geométrica crescente.
Progressão geométrica

35. Soma dos termos de uma PG
Elisa está montando sua árvore genealógica. Veja o que
ela já fez:

36. O número de pessoas a cada geração forma uma
PG: (1, 2, 4, 8, ...)
Para encontrar o número de antepassados de
Elisa, somamos os termos da PG formada até a
geração em questão.
Soma dos termos de uma PG

37. 8. TÓPICOS DE
GEOMETRIA PLANA

38. Classificação dos ângulos quanto às suas medidas:
Reto
Agudo
Obtuso
Ângulos

39. Um polígono de três lados
é um triângulo. Exemplos:
Triângulos
FABRICE
MICHAUDEAU/PANT
HERMEDIA/KEYDISC
Com a forma triangular, como o próprio
nome sugere, o triângulo de sinalização é
um equipamento de segurança
obrigatório e deve ser posicionado a 30
metros ou mais da parte traseira do
veículo, em local visível.

40. Dizemos que duas figuras
são semelhantes quando
uma delas é ampliação,
cópia ou redução da outra,
mantendo a mesma forma
e as proporções.
Semelhança
FRANCK
CAMHI/PANT
HERMEDIA/KEYDISC

41. Um feixe de retas paralelas interceptadas
por duas transversais determina, nessas
transversais, segmentos correspondentes
proporcionais.
Teorema de Tales

42. 9. TRIGONOMETRIA NO
TRIÂNGULO RETÂNGULO

43. Uma das faces deste monumento é
formada por um triângulo retângulo.
ADELANO
LÁZARO/CREATIVE
COMMONS
Centro Cultural Oscar Niemeyer em Goiânia, Goiás.

44. Razões Trigonométricas
no Triângulo Retângulo

45. Por meio das razões trigonométricas, conseguimos
calcular medidas.
Aplicação da Trigonometria
no Triângulo Retângulo

46. Ao projetarmos rampas, podemos perceber que,
quanto maior a inclinação, maior a força que precisa
ser exercida ao movimentar a carga.
Trigonometria e Física

47. Medindo ângulos: teodolito
Teodolito: instrumento que mede
ângulos, muito utilizado por topógrafos.
Modelo de teodolito de 1793,
construído em Londres por Edward
Troughton. Mogno, vidro e aço.
JBC
PROD/PANTHERMEDIA/KEYDISC
ÁLBUM/AKG-IMAGENS/LATINSTOCK