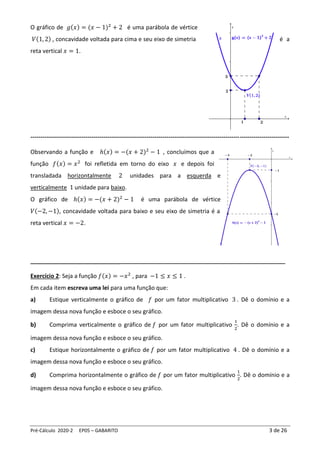
O documento fornece o gabarito de um exercício sobre transformações em gráficos de funções quadráticas. Nele, são explicadas as transformações que ocorrem nos gráficos quando se multiplica ou divide a função por uma constante, quando se soma ou subtrai uma constante da variável x ou y, e como isso afeta o vértice e o eixo de simetria das parábolas. Além disso, são solicitados esboços de gráficos de novas funções obtidas a partir de transformações em funções dadas.


![Pré-Cálculo 2020-2 EP05 – GABARITO 4 de 26
Resolução:
O gráfico da função dada, 𝑓(𝑥) = −𝑥2
, −1 ≤ 𝑥 ≤ 1 é:
]
1
,
1
[
)
( −
=
f
Dom
a) A função 𝑓1 cujo gráfico estica verticalmente o gráfico
de 𝑓 por um fator multiplicativo 3 é:
𝑓1(𝑥) = 3𝑓(𝑥) = −3𝑥2
O domínio de 𝑓1 é o mesmo domínio de 𝑓, 𝐷𝑜𝑚(𝑓1) = [−1 , 1].
Mas, se −1 ≤ 𝑓(𝑥) ≤ 0, então, multiplicando a desigualdade por
3 , obtemos −3 ≤ 3 ∙ 𝑓(𝑥) ≤ 0 e Im(𝑓1) = [−3 , 0].
-----------------------------------------------------------------------------------------------------------------------------------
b) A função 𝑓2 cujo gráfico comprime verticalmente o gráfico de 𝑓 por um fator
multiplicativo
1
2
é:
𝑓2(𝑥) =
1
2
𝑓(𝑥) = −
1
2
𝑥2
O domínio de 2
f é o mesmo domínio de 𝑓,
𝐷𝑜𝑚(𝑓2) = [−1 , 1]. Mas, se −1 ≤ 𝑓(𝑥) ≤ 0, então,
multiplicando a desigualdade por
1
2
, obtemos
1
2
∙ (−1) ≤
1
2
∙ 𝑓(𝑥) ≤
1
2
∙ 0 ⟹
−
1
2
≤
1
2
𝑓(𝑥) ≤ 0 e portanto, Im(𝑓2) = [−
1
2
, 0]
-----------------------------------------------------------------------------------------------------------------------------------
c) A função 𝑓3 cujo gráfico estica horizontalmente o gráfico de 𝑓 por um fator multiplicativo 4
é:
𝑓3(𝑥) = 𝑓 (
1
4
𝑥) = − (
1
4
𝑥)
2
= −
1
16
𝑥2
Assim,
𝑥 ∈ 𝐷𝑜𝑚( 𝑓3) ⟹
1
4
𝑥 ∈ 𝐷𝑜𝑚(𝑓) ⟹ −1 ≤
1
4
𝑥 ≤ 1 ⟹ −4 ≤ 𝑥 ≤ 4 ⟹
𝐷𝑜𝑚(𝑓3) = [−4, 4]
Essa transformação não mexe com a imagem da função, pois o esticamento (alongamento) é
horizontal. Assim, Im(𝑓3) = Im(𝑓) = [−1 , 0]
]
0
,
1
[
)
(
Im −
=
f](https://image.slidesharecdn.com/pc2020-2ep05transformacoesemgraficosgabarito-221017201247-b0fd7c89/85/PC_2020-2_EP05_Transformacoes-em-Graficos_GABARITO-pdf-4-320.jpg)
![Pré-Cálculo 2020-2 EP05 – GABARITO 5 de 26
𝐷𝑜𝑚(𝑓3) = [−4, 4] Im(𝑓3) = [−1 , 0]
-----------------------------------------------------------------------------------------------------------------------------------
d) A função 4
f cujo gráfico comprime horizontalmente o gráfico de 𝑓 por um fator
multiplicativo
1
2
é:
𝑓
4(𝑥) = 𝑓(2 𝑥) = −(2𝑥)2
= −4𝑥2
Assim,
𝑥 ∈ 𝐷𝑜𝑚( 𝑓4) ⟹ 2 𝑥 ∈ 𝐷𝑜𝑚(𝑓) ⟹ −1 ≤ 2 𝑥 ≤ 1 ⟹ −
1
2
≤ 𝑥 ≤
1
2
⟹
𝐷𝑜𝑚(𝑓4) = [−
1
2
,
1
2
].
Essa transformação não mexe com a imagem da função,
pois a compressão é horizontal. Assim,
𝐷𝑜𝑚( 𝑓4) = [−
1
2
,
1
2
] e Im( 𝑓4) = Im(𝑓) = [−1 , 0]
Exercício 3: Esboce os gráficos das funções listadas abaixo. Eles podem ser obtidos do gráfico da
função 𝑓(𝑥) = |𝑥| por meio de translações horizontais e/ou translações verticais e/ou reflexões
em torno dos eixos coordenados e/ou modulações. Explique as transformações ocorridas.
a) 𝑔(𝑥) = |𝑥 − 4| b) ℎ(𝑥) = |𝑥 + 2| c) 𝑗(𝑥) = |𝑥| + 2
d) 𝑚(𝑥) = −|𝑥 + 2| e) 𝑛(𝑥) = 5 − |𝑥 + 2|
f) 𝑢(𝑥) = |𝑥 − 4| − 3 g) 𝑣(𝑥) = ||𝑥 − 4| − 3|.
Resolução:
a) O gráfico da função 𝑔(𝑥) = |𝑥 − 4| é uma translação horizontal para direita de 4 unidades
do gráfico da função "elementar" 𝑓(𝑥) = |𝑥|:](https://image.slidesharecdn.com/pc2020-2ep05transformacoesemgraficosgabarito-221017201247-b0fd7c89/85/PC_2020-2_EP05_Transformacoes-em-Graficos_GABARITO-pdf-5-320.jpg)



![Pré-Cálculo 2020-2 EP05 – GABARITO 10 de 26
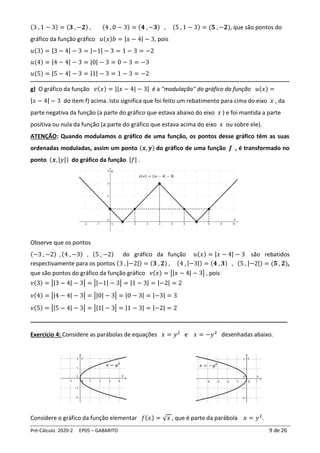
Para cada função:
𝑓1(𝑥) = −√𝑥 𝑓2(𝑥) = √−𝑥 𝑓3(𝑥) = −√−𝑥 𝑓4(𝑥) = √|𝑥| 𝑓5(𝑥) = −√|𝑥|,
faça o que se pede em cada item.
a) Determine o domínio da função.
b) Esboce o seu gráfico usando reflexões e/ou modulações a partir do gráfico da função 𝑓(𝑥) =
√𝑥.
c) Observe o gráfico e dê a imagem da função.
d) O gráfico obtido no item (b) é parte ou união de partes das parábolas de equações 𝑥 = 𝑦2
e/ou 𝑥 = −𝑦2
. Relacione o gráfico ou cada parte do gráfico obtido no item (b), com uma das duas
equações, citando em quais intervalos do eixo 𝑥 e do eixo 𝑦 a equação é identificada. Para relacionar
será preciso substituir o nome da função ( 𝑓1 , 𝑓2 , 𝑓3 , 𝑓
4 ou 𝑓5) por 𝑦 para obter uma equação
nas variáveis 𝑥 e 𝑦, depois elevar essa equação ao quadrado.
Resolução:
a) Como só é possível calcular a raiz quadrada de números positivos ou nulo, então
𝐷𝑜𝑚 (𝑓1) = {𝑥 ∈ ℝ; 𝑥 ≥ 0} = [0, ∞)
𝐷𝑜𝑚 (𝑓2) = 𝐷𝑜𝑚 (𝑓3) = {𝑥 ∈ ℝ; −𝑥 ≥ 0} = {𝑥 ∈ ℝ; 𝑥 ≤ 0} = (−∞, 0]
𝐷𝑜𝑚 (𝑓4) = 𝐷𝑜𝑚 (𝑓5) = {𝑥 ∈ ℝ; |𝑥| ≥ 0} = ℝ = (−∞, ∞) , pois |𝑥| ≥ 0 para qualquer 𝑥 ∈ ℝ.
-----------------------------------------------------------------------------------------------------------------------------------
b) Para auxiliar, esboçamos primeiro o
gráfico de 𝑓(𝑥) = √𝑥.
Gráfico de 𝒇𝟏(𝒙) = −√𝒙 :
Para esboçarmos o gráfico de 𝑦 = −𝑓(𝑥)
devemos refletir no eixo 𝑥 o gráfico de 𝑦 = 𝑓(𝑥). Portanto, o
gráfico de 𝑓1(𝑥) = −√𝑥 é obtido quando refletimos o gráfico de
𝑓(𝑥) = √𝑥 no eixo 𝑥.
Gráfico de 𝒇𝟐(𝒙) = √−𝒙 :
Para esboçarmos o gráfico de 𝑦 = 𝑓(−𝑥) devemos refletir o
gráfico de 𝑦 = 𝑓(𝑥) no eixo 𝑦. Portanto, o gráfico de
𝑓2(𝑥) = √−𝑥 é obtido quando refletimos o gráfico de
𝑓(𝑥) = √𝑥 no eixo 𝑦.](https://image.slidesharecdn.com/pc2020-2ep05transformacoesemgraficosgabarito-221017201247-b0fd7c89/85/PC_2020-2_EP05_Transformacoes-em-Graficos_GABARITO-pdf-10-320.jpg)
![Pré-Cálculo 2020-2 EP05 – GABARITO 11 de 26
Gráfico de 𝒇𝟑(𝒙) = −√−𝒙 :
Para esboçarmos o gráfico de 𝒚 = −𝒇(−𝒙) devemos refletir o gráfico
de 𝑦 = 𝑓(𝑥) no eixo 𝑥 para obter o gráfico de 𝑦 = −𝑓(𝑥) e depois
devemos refletir o gráfico de 𝑦 = −𝑓(𝑥) no eixo 𝑦, para obter o
gráfico de 𝑦 = −𝑓(−𝑥). Portanto, o gráfico de 𝑓3(𝑥) = −√−𝑥 é
obtido quando refletimos o gráfico de 𝑓(𝑥) = √𝑥 no eixo 𝑥 para
obter o gráfico de 𝑓1(𝑥) = −√𝑥 e depois, devemos refletir no eixo 𝑦 o gráfico de 𝑓1(𝑥) = −√𝑥 ,
para obter o gráfico de 𝑓3(𝑥) = −√−𝑥 .
Gráfico de 𝒇𝟒(𝒙) = √|𝒙| :
Para esboçarmos o gráfico de 𝒚 = 𝒇(|𝒙|) , devemos manter o gráfico de 𝑦 = 𝑓(𝑥) para 𝑥 ≥ 0 e
devemos refletir essa mesma parte, onde 𝑥 ≥ 0 , em relação ao eixo 𝑦 , pois
𝑦 = 𝑓(|𝑥|) = {
𝑓(𝑥) , 𝑠𝑒 𝑥 ≥ 0
𝑓(−𝑥) , 𝑠𝑒 𝑥 < 0
Portanto,
𝑓
4(𝑥) = √|𝑥| = {
√𝑥 , 𝑠𝑒 𝑥 ≥ 0
√−𝑥 , 𝑠𝑒 𝑥 < 0
Gráfico de 𝒇𝟓(𝒙) = −√|𝒙| :
Para esboçarmos o gráfico de 𝒇𝟓(𝒙) =
−√|𝒙| devemos refletir o gráfico de
𝑓4(𝑥) = √|𝑥| no eixo 𝑥
----------------------------------------------------------------------------------------------------------------------------------
c) Observando cada gráfico,
𝐼𝑚 (𝑓1) = {𝑦 ∈ ℝ; 𝑦 ≤ 0} = (−∞, 0] 𝐼𝑚 (𝑓2) = {𝑦 ∈ ℝ; 𝑦 ≥ 0} = [0, ∞)
𝐼𝑚 (𝑓3) = {𝑦 ∈ ℝ; 𝑦 ≤ 0} = (−∞, 0] 𝐼𝑚 (𝑓
4) = {𝑦 ∈ ℝ; 𝑦 ≥ 0} = [0, ∞)
𝐼𝑚 (𝑓5) = {𝑦 ∈ ℝ; 𝑦 ≤ 0} = (−∞, 0]
-----------------------------------------------------------------------------------------------------------------------------------](https://image.slidesharecdn.com/pc2020-2ep05transformacoesemgraficosgabarito-221017201247-b0fd7c89/85/PC_2020-2_EP05_Transformacoes-em-Graficos_GABARITO-pdf-11-320.jpg)


![Pré-Cálculo 2020-2 EP05 – GABARITO 14 de 26
𝑦 = √𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑑𝑖𝑟𝑒𝑖𝑡𝑎 𝑑𝑒
3 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝑦 = √𝑥 − 3
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑏𝑎𝑖𝑥𝑜 𝑑𝑒
2 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝐹(𝑥) = √𝑥 − 3 − 2
Portanto, o gráfico da função 𝐹(𝑥) = √𝑥 − 3 − 2 é obtido a partir do gráfico da função
𝑦 = √𝑥 , após a sequência de transformações descritas acima.
𝑎𝑝ó𝑠 𝑠𝑒𝑞𝑢ê𝑛𝑐𝑖𝑎
𝑑𝑒 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎çõ𝑒𝑠
→
𝐷𝑜𝑚(𝐹) = [3 , +∞) e Im(𝐹) = [−2 , +∞)
-----------------------------------------------------------------------------------------------------------------------------------
b) Vamos descrever uma sequência de transformações a partir do gráfico da função elementar
𝑦 = √𝑥 que nos levará ao gráfico da função 𝐺(𝑥) = 1 − √𝑥 + 4 .
𝑦 = √𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑎 𝑑𝑒
4 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝑦 = √𝑥 + 4
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑥
→ 𝑦 = −√𝑥 + 4
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑐𝑖𝑚𝑎 𝑑𝑒
1 𝑢𝑛𝑖𝑑𝑎𝑑𝑒
→ 𝐺(𝑥) = 1 − √𝑥 + 4
Portanto, o gráfico da função 𝐺(𝑥) = 1 − √𝑥 + 4 é obtido a partir do gráfico da função
𝑦 = √𝑥 , após a sequência de transformações descritas acima.
𝑎𝑝ó𝑠 𝑠𝑒𝑞𝑢ê𝑛𝑐𝑖𝑎
𝑑𝑒 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎çõ𝑒𝑠
→
𝐷𝑜𝑚(𝐺) = [−4 , +∞) e Im(𝐺) = (−∞ , 1]
-----------------------------------------------------------------------------------------------------------------------------------](https://image.slidesharecdn.com/pc2020-2ep05transformacoesemgraficosgabarito-221017201247-b0fd7c89/85/PC_2020-2_EP05_Transformacoes-em-Graficos_GABARITO-pdf-14-320.jpg)
![Pré-Cálculo 2020-2 EP05 – GABARITO 15 de 26
c) Vamos descrever uma sequência de transformações a partir do gráfico da função elementar
𝑦 = √𝑥 que nos levará ao gráfico da função 𝐻(𝑥) = √9 − 𝑥 − 2
𝑦 = √𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑎 𝑑𝑒
9 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝑦 = √𝑥 + 9
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑦
(𝑡𝑟𝑜𝑐𝑎𝑟 𝑥 𝑝𝑜𝑟−𝑥)
→ 𝑦 = √−𝑥 + 9
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑏𝑎𝑖𝑥𝑜 𝑑𝑒
2 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝐻(𝑥) = √9 − 𝑥 − 2
Portanto, o gráfico da função 𝐻(𝑥) = √9 − 𝑥 − 2 é obtido a partir do gráfico da função
𝑦 = √𝑥 , após a sequência de transformações descritas acima.
𝑎𝑝ó𝑠 𝑠𝑒𝑞𝑢ê𝑛𝑐𝑖𝑎
𝑑𝑒 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎çõ𝑒𝑠
→
𝐷𝑜𝑚(𝐻) = (−∞ ,9] e Im(𝐻) = [−2 , +∞)
Podemos descrever uma outra sequência de transformações que também nos levará ao gráfico de
𝐻(𝑥) = √9 − 𝑥 − 2 = √−(−9 + 𝑥) − 2 = √−(𝑥 − 9) − 2.
𝑦 = √𝑥
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑦
(𝑡𝑟𝑜𝑐𝑎𝑟 𝑥 𝑝𝑜𝑟−𝑥)
→ 𝑦 = √−𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑑𝑖𝑟𝑒𝑖𝑡𝑎 𝑑𝑒
9 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝑦 = √−(𝑥 − 9)
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑏𝑎𝑖𝑥𝑜 𝑑𝑒
2 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝐻(𝑥) = √9 − 𝑥 − 2
ATENÇÃO: cuidado ao fazer a translação horizontal 𝒚 = √−𝒙
𝒕𝒓𝒂𝒏𝒔𝒍𝒂çã𝒐 𝒉𝒐𝒓𝒊𝒛𝒐𝒏𝒕𝒂𝒍
𝒑𝒂𝒓𝒂 𝒅𝒊𝒓𝒆𝒊𝒕𝒂 𝒅𝒆
𝟗 𝒖𝒏𝒊𝒅𝒂𝒅𝒆𝒔
→ 𝒚 = √−(𝒙 − 𝟗).
A modificação deve ser feita na variável 𝒙 e não em −𝒙 . Por isso para obtermos o radicando
𝟗 − 𝒙 é preciso fazer uma translação horizontal para direita de 𝟗 unidades e assim, teremos
−(𝒙 − 𝟗) = −𝒙 + 𝟗 = 𝟗 − 𝒙.
-----------------------------------------------------------------------------------------------------------------------------------
d) Vamos descrever uma sequência de transformações a partir do gráfico da função elementar
𝑦 = √𝑥 que nos levará ao gráfico da função 𝐽(𝑥) = 3 − √4 − 𝑥 .
𝑦 = √𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑎 𝑑𝑒
4 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝑦 = √𝑥 + 4
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑦
(𝑡𝑟𝑜𝑐𝑎𝑟 𝑥 𝑝𝑜𝑟−𝑥)
→ 𝑦 = √−𝑥 + 4
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑥
→ 𝑦 = −√4 − 𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑐𝑖𝑚𝑎 𝑑𝑒
3 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝐽(𝑥) = 3 − √4 − 𝑥
Portanto, o gráfico da função 𝐽(𝑥) = 3 − √4 − 𝑥 é obtido a partir do gráfico da função
𝑦 = √𝑥 , após a sequência de transformações descritas acima.](https://image.slidesharecdn.com/pc2020-2ep05transformacoesemgraficosgabarito-221017201247-b0fd7c89/85/PC_2020-2_EP05_Transformacoes-em-Graficos_GABARITO-pdf-15-320.jpg)
![Pré-Cálculo 2020-2 EP05 – GABARITO 16 de 26
𝑎𝑝ó𝑠 𝑠𝑒𝑞𝑢ê𝑛𝑐𝑖𝑎
𝑑𝑒 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎çõ𝑒𝑠
→
𝐷𝑜𝑚(𝐽) = (−∞ ,4] e Im(𝐽) = [−∞ , 3)
Podemos descrever outras sequências de transformações que também nos levará ao gráfico
𝐽(𝑥) = 3 − √4 − 𝑥 = 3 − √−(−4 + 𝑥) = 3 − √−(𝑥 − 4)
𝑦 = √𝑥
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑦
(𝑡𝑟𝑜𝑐𝑎𝑟 𝑥 𝑝𝑜𝑟−𝑥)
→ 𝑦 = √−𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑑𝑖𝑟𝑒𝑖𝑡𝑎 𝑑𝑒
4 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝑦 = √−(𝑥 − 4)
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑥
→ 𝑦 = −√4 − 𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑐𝑖𝑚𝑎 𝑑𝑒
3 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝐽(𝑥) = 3 − √4 − 𝑥
Uma outra sequência de transformações que também nos levará ao gráfico 𝐽(𝑥) = 3 − √4 − 𝑥 .
𝑦 = √𝑥
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑥
→ 𝑦 = −√𝑥
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑎 𝑑𝑒
4 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝑦 = −√𝑥 + 4
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜
𝑛𝑜 𝑒𝑖𝑥𝑜 𝑦
(𝑡𝑟𝑜𝑐𝑎𝑟 𝑥 𝑝𝑜𝑟−𝑥)
→ 𝑦 = −√−𝑥 + 4
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑐𝑖𝑚𝑎 𝑑𝑒
3 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝐽(𝑥) = 3 − √4 − 𝑥
Ainda existem outras. Tente uma nova sequência de translações!!!
-----------------------------------------------------------------------------------------------------------------------------------
e) Vamos descrever uma sequência de transformações a partir do gráfico da função elementar
𝑦 = √𝑥 que nos levará ao gráfico da função 𝐾(𝑥) = √|𝑥 − 4| − 3.
𝑦 = √𝑥
𝑚𝑜𝑑𝑢𝑙𝑎çã𝑜 𝑑𝑎
𝑣𝑎𝑟𝑖á𝑣𝑒𝑙 𝑥
→ 𝑦 = √|𝑥|
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑑𝑖𝑟𝑒𝑖𝑡𝑎 𝑑𝑒
4 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝑦 = √|𝑥 − 4|
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑏𝑎𝑖𝑥𝑜 𝑑𝑒
3 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
→ 𝐾(𝑥) = √|𝑥 − 4| − 3
𝑎𝑝ó𝑠 𝑠𝑒𝑞𝑢ê𝑛𝑐𝑖𝑎
𝑑𝑒 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎çõ𝑒𝑠
→
𝐷𝑜𝑚(𝐾) = ℝ e Im(𝐾) = [−3 , +∞)](https://image.slidesharecdn.com/pc2020-2ep05transformacoesemgraficosgabarito-221017201247-b0fd7c89/85/PC_2020-2_EP05_Transformacoes-em-Graficos_GABARITO-pdf-16-320.jpg)


![Pré-Cálculo 2020-2 EP05 – GABARITO 19 de 26
𝑎𝑝ó𝑠 𝑠𝑒𝑞𝑢ê𝑛𝑐𝑖𝑎
𝑑𝑒 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎çõ𝑒𝑠
→
𝐷𝑜𝑚(𝐹) = (−∞ , −1] ∪ [1 , +∞) e Im(𝐹) = [−2 , +∞)
-----------------------------------------------------------------------------------------------------------------------------------
b) Construímos o gráfico de 𝐺(𝑥) = |(𝑥 + 1)3
− 1| fazendo as seguintes transformações em
gráficos:
𝑦 = 𝑥3
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜
ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
1 𝑢𝑛𝑖𝑑𝑎𝑑𝑒
𝑝𝑎𝑟𝑎 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑎
⇒ 𝑦 = (𝑥 + 1)3
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜
𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
1 𝑢𝑛𝑖𝑑𝑎𝑑𝑒
𝑝𝑎𝑟𝑎 𝑏𝑎𝑖𝑥𝑜
⇒ 𝑦 = (𝑥 + 1)3
− 1
Modulando
a função
𝑦=(𝑥+1)3−1
⇒ 𝐺(𝑥) = |(𝑥 + 1)3
− 1|
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜
𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
1 𝑢𝑛𝑖𝑑𝑎𝑑𝑒
𝑝𝑎𝑟𝑎 𝑏𝑎𝑖𝑥𝑜
⇒
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜
ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
1 𝑢𝑛𝑖𝑑𝑎𝑑𝑒
𝑝𝑎𝑟𝑎 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑎
⇒
Modulando
a função
𝑦=(𝑥+1)3−1
⇒
𝐷𝑜𝑚(𝐺) = ℝ e Im(𝐺) = [0 , +∞)](https://image.slidesharecdn.com/pc2020-2ep05transformacoesemgraficosgabarito-221017201247-b0fd7c89/85/PC_2020-2_EP05_Transformacoes-em-Graficos_GABARITO-pdf-19-320.jpg)






