Solidossecres

GEOMETRIA DESCRITIVA A 11.º Ano Sólidos III e Secções - Resumo © antónio de campos, 2010

GENERALIDADES – Sólidos III Para os sólidos com as bases contidas em planos oblíquos, planos de rampa ou planos passantes, um processo de resolução passa pelas seguintes acções: 1. Determinar as projecções da base , recorrendo ao rebatimento do plano que contém a base, para construir em V.G. a base, para depois inverter o rebatimento para obter as projecções; 2. Obter a altura do sólido , recorrendo a uma recta ortogonal ao plano da base, que será o eixo do sólido, rebater o eixo (via plano projectante) para obter a V.G. da altura, para depois inverter o rebatimento para obter as projecções; 3. Construir o sólido , a partir das projecções de todos os vértices, determinando a visibilidade, com os vértices com menor afastamento a estarem menos visíveis em projecção frontal, juntamente com todas as arestas que nele convergem, e os vértices com menor cota a estarem menos visíveis em projecção horizontal, juntamente com todas as arestas que nele convergem.

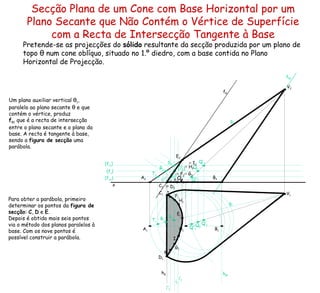
Projecção de uma Pirâmide com Base Contida em Plano Oblíquo São dados dois pontos, A (4; 0) e B (0; 3), contidos num plano oblíquo α . O traço horizontal do plano α faz um ângulo de 60º (a.e.) com o eixo x , enquanto o traço frontal faz um ângulo de 45º (a.e.) com o eixo x . Os pontos A e B são dois vértices consecutivos de um quadrado [ ABCD ] e a base de uma pirâmide quadrangular regular, com 7 cm de altura e situada no 1.º diedro. Desenha as projecções da pirâmide. Desenho à escala de 1:2. h α f α Determinar as projecções do quadrado, recorrendo do rebatimento do plano α para o Plano Horizontal de Projecção, com h α como charneira, para obter a V.G. ; e depois inverter o rebatimento, através de rectas frontais. Localizar o ponto O . ≡ e 1 ≡ h αr f αr ≡ A r f r f 1 f 2 f’ r f’ 1 f’ 2 Construir a pirâmide, com uma recta ortogonal p ao plano α , que será o eixo da pirâmide. O ponto V é o vértice da pirâmide. Para obter a V.G. do segmento de recta [OV], rebater um plano projectante (plano de topo δ ) que contém a recta p , com h δ como charneira, rebatendo a própria recta p . p 1 ≡ e 2 p 2 ≡ f δ h δ ≡ e’ 1 ≡ h δ r ≡ f δ r ≡ H’’ 2 p r Invertendo o rebatimento do plano δ , obtêm-se as projecções de V sobre as projecções homónimas da recta p , permitindo a construção da pirâmide. Na determinação da visibilidade, os vértices com menor afastamento estão menos visíveis em projecção frontal, juntamente com todas as arestas que nele convergem; os vértices com menor cota estão menos visíveis em projecção horizontal, juntamente com todas as arestas que nele convergem. x A 2 A 1 B 2 B 1 B r C r D r H 2 H r ≡ H 1 C 2 C 1 H’ 2 H’ r ≡ H’ 1 D 2 D 1 O 2 O 1 (e’ 2 ) O r H’’ r ≡ H’’ 1 V r V 2 V 1

FIGURA DA SECÇÃO E O SÓLIDO TRUNCADO Em baixo à esquerda, a figura da secção é a figura plana resultante da secção produzida no sólido pelo plano secante, com o sólido a permanecer indiviso. A B C D V A’ B’ C’ D’ A B C D A’ B’ C’ D’ V A’ B’ C’ D’ Em baixo à direita, o sólido truncado é um sólido, parte do sólido dado, compreendido entre o plano secante (a figura da secção) e a base ou o vértice.

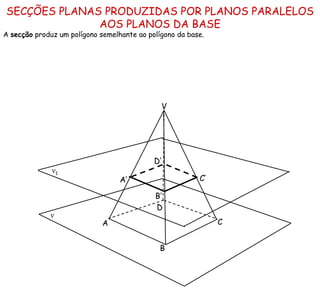
SECÇÕES PLANAS PRODUZIDAS POR PLANOS PARALELOS AOS PLANOS DA BASE A secção produz um polígono semelhante ao polígono da base. ν ν 1 A B C D V A’ B’ C’ D’

Secção Plana de uma Pirâmide com Base Horizontal Um sólido resultante da secção produzida por um plano horizontal ν numa pirâmide pentagonal regular, com a base contida no Plano Horizontal de Projecção. (f ν ) x K 1 ≡ V 1 A 2 A 1 C 2 C 1 B 2 B 1 D 2 D 1 E 2 E 1 V 2 K 2 M 2 M 1 N 2 N 1 O 2 O 1 P 2 P 1 Q 2 Q 1

GENERALIDADES – Cones Antes de determinar a figura da secção produzida por um plano num cone, é necessário identificar o tipo de secção . Para cones contidos em planos horizontais ou frontais, se o plano secante é paralelo à base do cone, a figura de secção é uma circunferência . O processo de identificação do tipo de secção produzida passa pelos seguintes passos, se o plano secante conter o vértice de superfície : 1 – Determinar a recta de intersecção do plano secante com o plano da base do cone; 2 – Analisar a posição da recta de intersecção em relação à base do cone; a) – se a recta de intersecção é exterior à base, a figura da secção é um ponto ; b) - se a recta de intersecção é tangente à base, a figura da secção é uma recta ; c) - se a recta de intersecção é secante à base, a figura da secção é um triângulo . O processo de identificação do tipo de secção produzida passa pelos seguintes passos, se o plano secante não conter o vértice de superfície : 1 – Conduzir pelo vértice do cone, um plano paralelo ao plano secante; 2 – Determinar a recta de intersecção do plano paralelo com o plano da base do cone; 3 – Analisar a posição da recta de intersecção em relação à base do cone; a) – se a recta de intersecção é exterior à base, a figura da secção é uma elipse ; b) - se a recta de intersecção é tangente à base, a figura da secção é uma parábola ; c) - se a recta de intersecção é secante à base, a figura da secção é uma hipérbole .

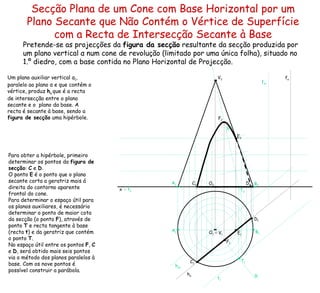
Secção Plana de um Cone com Base Horizontal por um Plano Secante que Contém o Vértice de Superfície com a Recta de Intersecção Secante à Base Um sólido resultante da secção produzida por um plano de topo δ num cone oblíquo, com a base contida no Plano Horizontal de Projecção.. h δ f δ ≡ D 2 O h δ é a recta de intersecção entre o plano secante e o plano da base do cone. A recta é secante à base. O triângulo [ CDV ] é a figura de secção . x A 2 A 1 O 2 O 1 B 2 B 1 V 2 V 1 C 1 C 2 D 1

Secção Plana de um Cone com Base Frontal por um Plano Secante que Não Contém o Vértice de Superfície com a Recta de Intersecção Exterior à Base Pretende-se as projecções da figura de secção resultante da secção produzida por um plano vertical α num cone de revolução, situado no 1.º diedro, com a base contida no Plano Frontal de Projecção. ≡ V 2 h α f α h θ Um plano auxiliar vertical θ , paralelo ao plano α e que contém o vértice, produz f θ que é a recta de intersecção entre o plano secante e o plano da base. A recta é exterior à base, sendo a figura de secção uma elipse. f θ Utilizar o método dos planos paralelos à base para obter a elipse: 1 – Plano auxiliar paralelo ao plano da base; 2 – A figura de secção (circunferência) do plano auxiliar sobre superfície lateral do sólido; 3 – Recta de intersecção entre plano secante e plano auxiliar; 4 – Pontos de intersecção da recta de intersecção com a circunferência. (h φ ) i 2 ≡ E 1 ≡ F 1 A seguir, construir o eixo menor da elipse, com o ponto M a ser o ponto de concorrência dos dois eixos da elipse. Depois é obtido mais quatro pontos via o método dos planos paralelos à base. Com os oito pontos é possível construir a elipse. ≡ M 1 (h φ1 ) i’ 2 ≡ G 1 ≡ H 1 (h φ2 ) i’’ 2 ≡ I 1 ≡ J 1 ≡ Q 2 x O 2 O 1 V 1 A 2 A 1 B 2 B 1 C 2 C 1 D 2 D 1 R 2 R 1 Q 1 (i 1 ) E 2 F 2 M 2 S 2 S 1 (i’ 1 ) G 2 H 2 T 2 T 1 I 2 (i’’ 1 ) J 2

Secção Plana de um Cone com Base Horizontal por um Plano Secante que Não Contém o Vértice de Superfície com a Recta de Intersecção Tangente à Base Pretende-se as projecções do sólido resultante da secção produzida por um plano de topo θ num cone oblíquo, situado no 1.º diedro, com a base contida no Plano Horizontal de Projecção. h θ f θ ≡ D 2 Um plano auxiliar vertical θ 1 , paralelo ao plano secante θ e que contém o vértice, produz f θ 1 que é a recta de intersecção entre o plano secante e o plano da base. A recta é tangente à base, sendo a figura de secção uma parábola. f θ 1 h θ 1 Para obter a parábola, primeiro determinar os pontos da figura de secção : C , D e E . Depois é obtido mais seis pontos via o método dos planos paralelos à base. Com os nove pontos é possível construir a parábola. g 1 g 2 (f ν ) i 1 ≡ F 2 ≡ G 2 (f ν 1 ) i’ 1 ≡ H 2 (f ν 2 ) i’’ 1 ≡ J 2 ≡ K 2 ≡ I 2 x A 2 A 1 O 2 O 1 B 2 B 1 V 2 V 1 C 1 C 2 D 1 E 2 E 1 Q 2 Q 1 R 2 R 1 (i 2 ) F 1 G 1 Q’ 2 Q’ 1 S 2 S 1 (i’ 2 ) H 1 I 1 T 2 T 1 Q’’ 2 Q’’ 1 (i’’ 2 ) J 1 K 1

Secção Plana de um Cone com Base Horizontal por um Plano Secante que Não Contém o Vértice de Superfície com a Recta de Intersecção Secante à Base Pretende-se as projecções da figura da secção resultante da secção produzida por um plano vertical α num cone de revolução (limitado por uma única folha), situado no 1.º diedro, com a base contida no Plano Horizontal de Projecção. ≡ V 1 h α f α Um plano auxiliar vertical α 1 , paralelo ao plano α e que contém o vértice, produz h α que é a recta de intersecção entre o plano secante e o plano da base. A recta é secante à base, sendo a figura de secção uma hipérbole. h α 1 f α 1 Para obter a hipérbole, primeiro determinar os pontos da figura de secção : C e D . O ponto E é o ponto que o plano secante corta a geratriz mais á direita do contorno aparente frontal do cone. Para determinar o espaço útil para os planos auxiliares, é necessário determinar o ponto de maior cota da secção (o ponto F ), através de ponto T e recta tangente à base (recta t ) e da geratriz que contém o ponto T . No espaço útil entre os pontos F , C e D , será obtido mais seis pontos via o método dos planos paralelos à base. Com os nove pontos é possível construir a parábola. t 1 ≡ t 2 g 1 g 2 x O 2 O 1 V 2 A 2 A 1 B 2 B 1 C 2 C 1 D 2 D 1 E 2 E 1 T 2 T 1 F 2 F 1

GENERALIDADES – Cilindros Antes de determinar a figura da secção produzida por um plano num cilindro, é necessário identificar o tipo de secção , para cilindros contidos em planos horizontais ou frontais. Se o plano secante é paralelo aos planos das bases, a figura de secção é uma circunferência . Para situações em que o plano secante não é paralelo aos planos das bases: Se o plano secante é paralelo ao eixo da superfície do cilindro e o plano secante é tangente à superfície ao longo de uma geratriz, a figura de secção é uma recta ; Se o plano secante é paralelo ao eixo da superfície do cilindro e o plano secante secciona a superfície ao longo de duas geratrizes, a figura de secção é um paralelograma ; Se o plano secante não é paralelo ao eixo da superfície do cilindro, a figura de secção é uma elipse .

Secção Plana de um Cilindro com Bases Horizontais por um Plano Secante Não Paralelo aos Planos das Bases, Paralelo ao Eixo da Superfície e Secciona a Superfície ao Longo de Duas Geratrizes Um sólido resultante da secção produzida por um plano vertical α num cilindro de revolução, com as bases contidas em planos horizontais ν e ν 1 . (f ν ) ≡ A’ 1 ≡ O’ 1 ≡ B’ 1 (f ν 1 ) f α h α g 2 g’ 2 ≡ C 1 ≡ C’ 1 ≡ D 1 ≡ D’ 1 x A 2 A 1 B 2 B 1 O 2 O 1 O’ 2 B’ 2 A’ 2 (g 1 ) (g’ 1 ) C 2 C’ 2 D 2 D’ 2

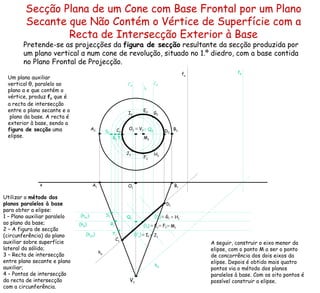
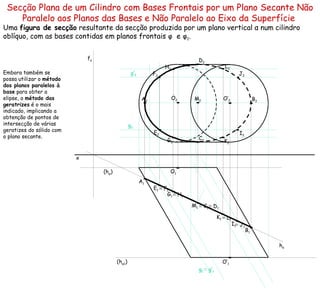
Secção Plana de um Cilindro com Bases Frontais por um Plano Secante Não Paralelo aos Planos das Bases e Não Paralelo ao Eixo da Superfície Uma figura de secção resultante da secção produzida por um plano vertical α num cilindro oblíquo, com as bases contidas em planos frontais φ e φ 1 . (h φ ) (h φ1 ) Embora também se possa utilizar o método dos planos paralelos à base para obter a elipse, o método das geratrizes é o mais indicado, implicando a obtenção de pontos de intersecção de várias geratizes do sólido com o plano secante. h α f α ≡ C 1 ≡ D 1 g 2 g’ 2 g 1 ≡ g’ 1 ≡ F 1 ≡ H 1 ≡ J 1 ≡ L 1 x O 2 O 1 O’ 2 O’ 1 A 2 A 1 B 2 B 1 M 2 M 1 C 2 D 2 E 2 E 1 F 2 G 2 G 1 H 2 I 2 I 1 J 2 K 2 K 1 L 2

GENERALIDADES – Secções sobre Esferas A figura de secção produzida por qualquer plano numa superfície esférica é sempre uma circunferência .

Secção Plana de uma Esfera por um Plano Secante Paralelo a um Plano de Projecção Uma figura de secção resultante da secção produzida por um plano frontal φ numa esfera, passando pelo ponto O, sendo assim o círculo máximo frontal da esfera. (h φ ) x O 2 O 1

GENERALIDADES – Secções Produzidas por Planos Não Projectantes Sobre Poliedros Para resolver situações de secções produzidas por planos não projectantes sobre poliedros, existem várias possibilidades, entre elas, destacam-se as seguintes: 1 – Mudança de diedro de projecção, transformando o plano secante em plano projectante, para depois aplicar o processo de secção igual a planos projectantes; 2 – Determinação dos pontos de intersecção de cada aresta com o plano secante, através da intersecção de uma recta com um plano não projectante (método geral da intersecção de rectas com planos); 3 – Método misto, determinação dos pontos de intersecção de cada aresta com o plano secante, e determinação das rectas de intersecção do plano secante com os planos que contém as faces do sólido.

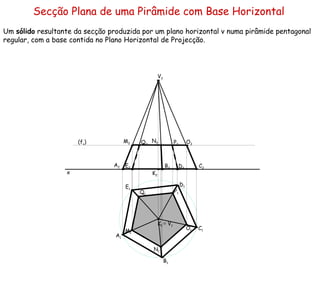
(h φ1 ) (h φ ) (h ρ ) Secção Plana de um Prisma por Plano Secante Não Projectante Pretende-se uma figura da secção produzida por um plano de rampa ρ num prisma quadrangular oblíquo, com as bases contidas em planos frontais. (f ρ ) Neste caso, será utilizado o segundo método: determinação dos pontos de intersecção de cada aresta com o plano secante, através da intersecção de uma recta com um plano não projectante (método geral da intersecção de rectas com planos). Primeiro há que determinar qual as arestas a serem cortadas. Como a recta de intersecção do plano ρ com o plano da base com maior afastamento (o plano φ 1 ) se situa no 2.º diedro, o plano secante não intersecta esta base. A seguir será determinada a recta de intersecção (recta i ) do plano secante (o plano ρ ) com o plano das base com menor afastamento, recorrendo a um plano auxiliar projectante (plano vertical α ). I é o ponto de intersecção da recta i com o plano φ . A recta g é a recta de intersecção do plano ρ com o plano φ . Como a recta g é exterior à base com menor afastamento, o plano secante não corta a base com menor afastamento do sólido. Depois começa a determinação dos pontos da figura de secção. M é o ponto de intersecção da recta i com a aresta [ AA’ ], sendo o ponto de intersecção da aresta com o plano secante, sendo um ponto da figura da secção . A seguir, serão determinados sucessivamente os pontos de intersecção das arestas laterais com o plano secante. h α f α ≡ i 1 i 2 h α 1 f α 1 h α 2 f α 2 h α 3 ≡ g 1 g 2 x A 2 A 1 B 2 B 1 C 2 C 1 D 2 D 1 A’ 2 A’ 1 B’ 2 B’ 1 C’ 2 C’ 1 D’ 2 D’ 1 F 2 F 1 H 2 H 1 M 2 M 1 N 2 N 1 O 2 O 1 P 2 P 1 I 2 ≡ I 1

GENERALIDADES – Secções Produzidas por Planos Não Projectantes Sobre Cones e Cilindros Para resolver situações de secções produzidas por planos não projectantes sobre cones e cilindros, é necessário um processo muito complexo , quer em termos de raciocínio, quer em termos de traçados. As etapas desse processo são as seguintes: 1 – Identificar o tipo de figura de secção; 2 – Verificar se o plano secante corta as bases; 3 – Determinar os pontos em que o plano secante corta as linhas que intersectam o contorno aparente; 4 – Determinar os pontos de maior e de menor cota da secção; 5 - Determinar os pontos de maior e de menor afastamento da secção; 6 – Determinar mais dois pontos, através do método dos planos paralelos à base .

Secção Plana de um Cone por Plano Secante Não Projectante Pretende-se um sólido resultante da secção produzida por um plano oblíquo α num cone de revolução, situado no 1.º diedro e com base no Plano Horizontal de Projecção. 1 - Identificar o tipo de figura de secção. Um plano auxiliar de topo θ 1 , paralelo ao plano θ e que contém o vértice. A recta r é a recta de intersecção entre o plano secante e o plano da base. A recta é exterior à base, sendo a figura de secção uma elipse. 2 – Verificar se o plano secante corta as bases. h α é a recta de intersecção do plano secante com o plano da base e é exterior à base, pelo que o plano secante não corta a base do cone. 3 – Determinar os pontos em que o plano secante corta as linhas que intersectam o contorno aparente. O plano φ é um plano auxiliar, que contém as duas geratrizes do contorno aparente frontal. A recta i é a recta de intersecção do plano φ com o plano secante. A e B são os pontos de intersecção das geratrizes do contorno aparente frontal com o plano secante. 4 – Determinar os pontos de maior e de menor cota da secção. Para tal, determinar os planos tangentes ( θ 1 e θ 2 ) do cone que intersectam o plano secante, via rectas horizontais. A recta h é a recta de intersecção dos dois planos tangentes. As rectas t e t ’ são as rectas de intersecção dos planos tangentes com o plano secante. C é o ponto de maior cota e D de menor cota da secção. ≡ V 1 f α h α f α 1 h α 1 (h φ ) ≡ i 1 i 2 g 1 ≡ g’ 1 g 2 g’ 2 h 1 h 2 h θ 1 h θ 2 f θ 1 f θ 2 t 1 t 2 t’ 1 t’ 2 ≡ f 1 ≡ f 2 h θ 3 h θ 4 g’’ 1 g’’’ 1 g’’ 2 ≡ g’’’ 2 s 1 s 2 s’ 1 s’ 2 (f ν ) ≡ i’ 2 i’ 1 5 - Determinar os pontos de maior e de menor afastamento da secção. Para tal, determinar os planos tangentes ( θ 3 e θ 4 ) do cone que intersectam o plano secante, via rectas frontais. A recta f é a recta de intersecção dos dois planos tangentes. As rectas s e s ’ são as rectas de intersecção dos planos tangentes com o plano secante. E é o ponto de menor afastamento e F de maior afastamento da secção. 6 – Determinar mais dois pontos, através do método dos planos paralelos à base . O plano ν é o plano horizontal paralelo à base. A recta i ’ é a recta de intersecção entre os planos ν e α . G e H são mais dois pontos. x O 2 O 1 V 2 H 2 H 1 A 2 A 1 B 2 B 1 F 2 F 1 F’ 2 F’ 1 F’’ 2 F’’ 1 C 2 C 1 D 2 D 1 H’ 2 H’ 1 H’’ 2 H’’ 1 H’’’ 2 H’’’ 1 E 2 E 1 F 2 F 1 F’’’ 2 F’’’ 1 G 2 G 1 H 2 H 1

Solidossecres

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Solidossecres

Solidossecres