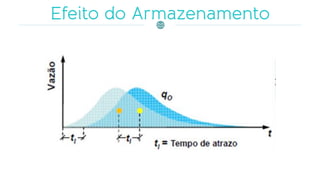
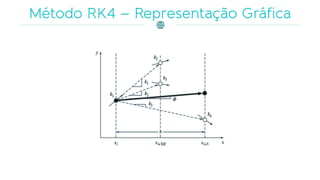
O documento discute métodos de propagação hidrológica e hidrodinâmica, como o Muskingun e o Método da Onda Cinemática. Explica conceitos como equação da continuidade, ondas dinâmicas e de difusão, e discretização da equação de Saint-Venant para modelagem unidimensional de escoamento em rios.

1. Francisco de Assis de Souza Filho

3. Propagação Hidrológica
• Método de propagação agregada (Lumped)
• Usa apenas a equação da continuidade
• Exemplo: Muskingun

4. Propagação Hidráulica
• Método de propagação Distribuído (necessita de seções transversais)
• Usa a equação da continuidade e do momento
• Descrição mais acurada do movimento da onda
• Exemplo: Método de Priesman

5. Canal Simples
Sistema Dendritico (tree-type)
Rio & Tributários
Canal & Distribuição
Delta do Rio
Rede

6. Modelagem Hidrológica
• Muskingun-Cunge
Modelagem Hidrodinâmica
• Onda Dinâmica
• Onda Cinemática

7. Reservatório:
Hidrograma de saída cai na
recessão do de entrada
Trecho de rio:
Hidrograma de saída defasado
com relação ao de entrada
V  volume de amortecimento

8. • Reservatórios longos e estreitos, canais e cursos de água em
que a superfície livre da água pode ser acentuadamente curva
devido ao regolfo.
• A relação entre a vazão de saída e o armazenamento deixa de
ser biunívoca, apresentando histerese.
• Se o efeito de regolfo não for muito importante pode
desprezar-se a histerese e aproximar-se a relação por uma única
curva.
• O armazenamento máximo continua a ocorrer quando os
hidrogramas se cruzam, isto é, quando:
• Devido ao efeito retardador do regolfo, a vazão de ponta
ocorre normalmente mais tarde que na intercepção com o
hidrograma de entrada.
Relação variável:

13. Método da Onda Dinâmica:
• Incluem termo inercial e de pressão.
• Ondas movem-se nas duas direções: montante e jusante.
• Exemplos: DAMBRK, DWOPER, FLDWAV, UNET, HEC-RAS (componente não
permanente).
Método da Onda de Difusão:
• Exclui termo inercial.
• Ondas movem-se apenas para jusante.
• Onda pode atenuar-se em seu movimento para jusante.
• Exemplo: Muskingum-Cunge.
Método da Onda Cinemática:
• Incluem termo inercial e de pressão.
• Ondas movem-se apenas para jusante.
• Exemplos: Eq. Manning, HEC-2, HEC-RAS (componente permanente).

14. Equação da Continuidade:
Preserva o volume de água no canal.
Equação do Momento:
Relação física que descreve o movimento das águas.

15. • Escoamento é 1-D: as características do escoamento (profundidade, vazão etc.)
variam apenas na direção longitudinal “x” do canal.
• A seção da água é horizontal em qualquer seção perpendicular ao eixo
longitudinal.
• Escoamento é gradualmente variado com pressões hidrostáticas em todos os
pontos do escoamento.

16. • A declividade do fundo do canal é pequena, i.e., tan(h) = sen(h).
• O fundo do canal é fixo.
• A resistência ao escoamento (perda de carga) é considerada similar a do
escoamento uniforme, permitindo-se a aplicação de equações empíricas como
a de Manning.
• Escoamento é incompressível.
• Densidade é homogênea.

17. ou
Onde:
Q = Vazão
A = Área da seção Transversal
x = Distância
t = Tempo
qL = Escoamento lateral
I = Afluência
O = Efluência
S = Armazenamento

18. Ou
Equação Conservativa
Resolvendo para Sf
Equação da Onda Dinâmica
Equação da Onda de Difusão
(Menos os temos inerciais)
Equação da Onda Cinemática
(Menos o temo de pressão)
Onde:
V = Velocidade
y = profundidade
t = tempo
x = distancia
g = aceleração da gravidade
So = declividade do fundo
Sf = perda de carga unitária

19. Baseada na Equação Completa de escoamento 1-D não permanente
(Equação de St. Venant)
Continuidade Momento
Onde: h = elevação da superfície de água é
A vazão (Q) e elevação da superfície da água (h) em
cada localidade no rio são calculadas usando equações
algébricas que representam a equação de Saint Venant.
Q e h são determinados no sistema fluvial para cada
intervalo de tempo. Utiliza-se diferenças finitas para a
determinação destas equações algébricas

21. • Equacionamento
• Vantagem: Robusto
• Limitações:
o Propagação da onda apenas para jusante
o Não é aplicável com efeitos de jusante significativo
o Não é aplicável para ondas com subida rápidas
• Resolução
o Linear
o Não Linear

22. Equacionamento
  q
t
Q
Q
x
Q





 1

Esquema de Discretização

24. Discretização da Equação Diferencial:
Equacionamento:

25.   q
t
Q
Q
x
Q





 1
Equacionamento

26. Equacionamento:
q
t
A
x
Q






Discretização da Equação Diferencial:
Sendo: e
Equacionamento:
Esquema de Discretização:
2
;
;
1
1
1
11
1
1
1
1
j
i
j
i
j
i
j
i
j
i
j
i
xx
tt

























27. q
t
A
x
Q






Equacionamento: Esquema de Discretização:
2
;
;
1
1
1
11
1
1
1
1
j
i
j
i
j
i
j
i
j
i
j
i
xx
tt

























28. Discretização da Equação Diferencial:
Sendo: e
Equacionamento:

29. Equacionamento:
Método de Newton-Rapson

31. Foi desenvolvido para o rio Muskingun em Ohio por Marcarthy (1939)
Armazenamento: Continuidade:
Equação diferencial
Equação Discretizada
Discretização
})1({ QXXIKS  QI
dt
dS

dt
dI
KXIQ
dt
dQ
XK  )1(
tttt QCICICQ 22111  
2
;
1
1
tt
tt
tdt
d










onde

32. Desenvolvimento de Cunge (1969)
tttt QCICICQ 22111  
Equação
Discretizada
Onde:
Estimativa dos
Parâmetros
Condição de
Estabilidade: e5,00  X )1(22 X
K
t
X 



33. Vantagens sobre o método padrão da onda Cinemática:
• a solução é obtida por uma equação algébrica linear em vez de uma diferença
finita ou aproximação característica de uma equação diferencial parcial; isto
permite obter o hidrograma inteiro no trecho de interesse sem necessitar
calcular várias seções e intervalos de tempo intermediários.
• Segundo tenderá a mostrar menos atenuação de onda e permitirá uma escolha
mais flexível de tempo e incrementos de espaço para as computações como
comparou ao método da onda cinemática.
A Inundação britânica inclusiva Estuda relatório (“Natural Environment Research
Council”, 1975) concluiu que o método de Muskingum-Cunge é preferível a
métodos que usam um modelo de onda de difusão por causa de sua
simplicidade; sua precisão é semelhante.

34. Desvantagens do método de Muskingum-Cunge são:
• não pode simular perturbações de jusante que se propaguem rio acima;
• não prediz o hidrograma de descarga com precisão se houver grandes
variações na celeridade da onda como as resultantes de grandes planícies de
inundação.

35. Equações de Saint-Venant:
Conservação da Massa
Conservação do Momento
Classificação:
0





q
t
A
x
Q
    00
2














xfef qBWSSSgA
x
h
gA
x
AQ
t
Q



36. Método da Onda Dinâmica:
• Incluem termo inercial e de pressão.
• Ondas movem-se nas duas direções montante e jusante.
• Exemplos: DAMBRK, DWOPER, FLDWAV, UNET, HEC-RAS (componente não
permanente).
Método da Onda de Difusão:
• Exclui termo inercial.
• Ondas movem-se apenas para jusante.
• Onda pode atenuar-se em seu movimento para jusante.
• Exemplo: Muskingum-Cunge.
Método da Onda Cinemática:
• Incluem termo inercial e de pressão.
• Ondas movem-se apenas para jusante.
• Exemplos: Eq. Manning, HEC-2, HEC-RAS (componente permanente).

38. Francisco de Assis de Souza Filho

39. Os reservatórios tem por objetivo acumular parte das águas disponíveis nos
períodos chuvosos para compensar as deficiências nos períodos de estiagem,
exercendo um efeito regularizador das vazões naturais.

40. Em geral os reservatórios são formados por meio de barragens implantadas nos
cursos d‘água. Suas características físicas, especialmente a capacidade de
armazenamento, dependem das características topográficas do vale em que
estão inseridos.

41. Propagação: procedimento matemático para determinar a variação da
magnitude, da velocidade e da forma de uma onda de cheia, em função do
tempo, num ou mais pontos de um curso de água ou de um reservatório.
•Modelação simples, mas com alguma base física.
•Recorre à equação da continuidade e a uma equação para
caracterizar o armazenamento de água no rio ou reservatório.
•Modela a variação temporal da Vazão num determinado ponto.
•Modelação normalmente agregada.
• Modelação com base física.
• Recorre à equação da continuidade e da conservação da quantidade de
movimento.
• O escoamento variável é normalmente considerado a uma dimensão (ao longo
do curso de água ou do reservatório), o que conduz às equações de Saint-Venant.
• Modela simultaneamente a variação temporal da vazão e da altura da água em
diferentes pontos do espaço.
• Modelação normalmente distribuída.

42. Um reservatório pode ser descrito por seus níveis e volumes característicos:
 Nível mínimo operacional
 Nível máximo operacional
 Volume máximo
 Volume morto
 Volume útil

44. Equação da continuidade:
QI
t
S



Intervalo de tempo curto: cheias
Intervalo de tempo longo: dimensionamento
Métodos gráficos
(antigos)
Simulação

45. Dados os hidrogramas de entrada no reservatório, qI(t), e de saída deste, qo(t),
representados na Figura, a forma diferencial da equação da continuidade é:
Em que S representa o armazenamento no reservatório.
A caracterização do sistema fica completa se se conhecer a relação S= f(qo). Esta relação
não se conhece normalmente de uma forma analítica, mas sim de uma forma tabular.

46. A relação entre o caudal de saída e o
armazenamento pode ser variável ou constante.
Relação constante:
• Reservatório com superfície horizontal
(larga e profunda, com reduzidas velocidades).
• Há uma descarga fixa para uma dada carga
h: S = f(qo)
• O armazenamento máximo ocorre
quando os hidrogramas se cruzam, isto é,
quando:
• Como S = f(qo), então ao máximo
armazenamento, Sm, corresponde o vazão máxima de saída, qOp.

48. O Método RK4 pode ser utilizado como alternativa ao Método de Plus na
modelagem de propagação de cheias e dimensionamento de vertedouros em
reservatórios.
A equação utilizada na propagação de cheias é:
• V é o volume da água no reservatório;
• I é vazão afluente ao reservatório devido à
precipitação;
• Q é a vazão efluente devido ao vertimento;
• L é o comprimento do vertedouro;
• H é a cota do nível da água em acima da cota do
vertedouro;
• y e C são coeficientes.

49. Esta equação pode ser resolvida pelo RK4 considerando variações nas vazões
durante o intervalo modelado, ao adotar:
• A vazão afluente como função do tempo I(t);
• A vazão efluente como função do volume de água no reservatório Q(V), uma
vez que H é função de V e é calculado pela CAV do reservatório;
Assim, as equações tornam-se:
A resolução da Propagação de Cheias, pelo método RK4, considerando I(t)
linear em função do tempo, estão apresentadas na planilha.

50. Os métodos de Runge-Kutta (RK) utilizam a extrapolação linear:
Onde,
yi+1 é o valor de y no final do intervalo;
yi é o valor de y no início do intervalo;
é o valor estimado da inclinação para o intervalo;
h é o tamanho do intervalo.
Para a resolução das equações diferenciais ordinárias de forma:

51. - Os métodos RK estimam o valor da inclinação (Ø) utilizada na extrapolação
linear a partir do valor da equação diferencial (dy/dx) no ponto inicial do
intervalo.
- Assim, a utilização dos métodos RK necessita dos valores da função e da
equação diferencial no ponto inicial como condições de contorno.
- Dentre os métodos RK, se destacam o de Euler, o de Heun e os de Quarta
Ordem.

52. É o método RK mais utilizado.
O método RK4 determina a inclinação da extrapolação linear a partir de 4 estimativas EDO
(derivada) no intervalo.
O método RK4 é dado por:
Ou seja:
Onde
• k1 é o valor da equação diferencial no início do intervalo;
• k2 é o valor da equação diferencial na metade do intervalo, no ponto estimado pela
extrapolação linear de inclinação k1;
• k3 é o valor da diferencial na metade do intervalo, no ponto estimado pela extrapolação linear
de inclinação k2;
• k4 é o valor da diferencial no final do intervalo, no ponto estimado pela extrapolação linear de
inclinação k3.

55. Considerando um reservatório com vertedor livre, em que a vazão de saída é
uma função do nível da água no reservatório, a equação abaixo pode ser
aplicada recursivamente:
2
QQ
2
II
t
SS ttttttttt  





Nesta equação, em cada intervalo de tempo são conhecidas as vazões de entrada
no tempo t e em t+t; a vazão de saída no intervalo de tempo t; e o volume
armazenado no intervalo t. Não são conhecidos os termos St+t e Qt+t , e
ambos dependem do nível da água.
Como tanto St+t e Qt+t são funções não lineares de ht +t , a equação de
balanço pode ser resolvida utilizando a técnica iterativa de Newton, ou ‘outro
método numérico.

56. Uma forma mais simples de calcular a propagação de vazão num reservatório
é o método conhecido como Puls modificado. Neste método a equação acima
é reescrita como:
t
t
ttttt
tt
Q
t
S2
IIQ
t
S2








Uma tabela da relação entre Qt+t e 2.(St+t )/t pode ser gerada a partir da
relação cota – área – volume do reservatório e através da relação entre a cota
e a vazão, por exemplo para uma equação de vertedor.
t
t
ttttt
tt
Q
t
S2
IIQ
t
S2









57. Equação da Continuidade
Incógnitas Variáveis
conhecidas
1 equação e 2 Incógnitas  equação adicional: Q = f(S/Dt)

58. Cálculo de Q e S
Q=f(S/DT)
Q=G(Q+2s/DT)
Q(t+1)
S(t+1)/ t

59. Função auxiliarQ = f(S/Dt) Q = f1(Q + 2.S/Dt)
Construídas a partir da curva cota x S e cota x Q saída pelas estruturas hidráulicas

60. Metodologia
1. Estabeleça as condições iniciais So (volume inicial)  calcular;
Q0 = f(S0/Dt) no gráfico Q = f(S/Dt);
2. Calcule o valor G = lado direito da equação acima;
3. Este valor é igual a f1 = lado esquerdo da equação acima;
4. No gráfico Q = f1(Q + 2.S/Dt)  determinar Qt+1 e St+1
5. Repete-se os itens 2 a 4 até o último intervalo de tempo.

61. Metodologia
Δt
2S
QII
Δt
2S
Q t
t1tt
1t
1t  


Q=f(S/DT) Q=f1(Q+2S/DT)
Qt+1
Cálculo de G com o hidrograma
de entrada
St+1/Dt