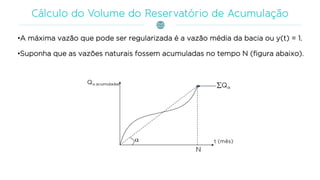
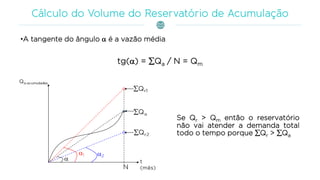
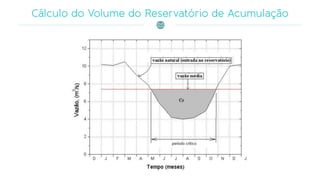
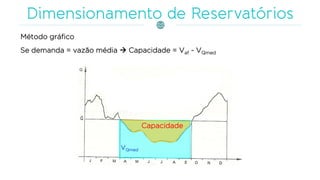
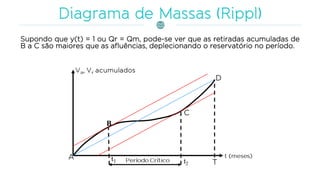
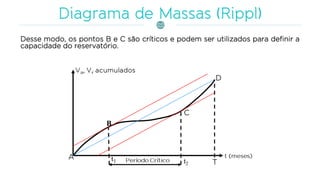
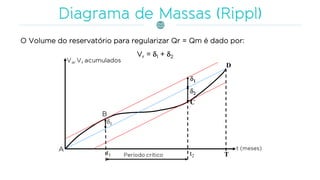
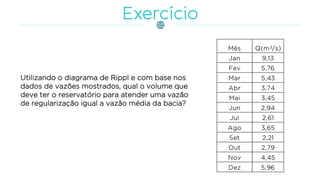
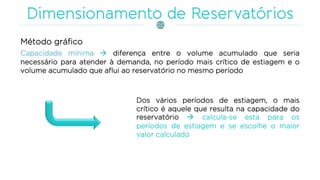
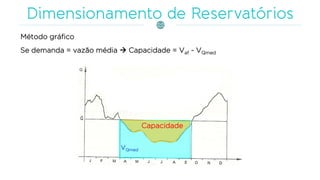
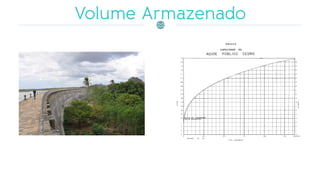
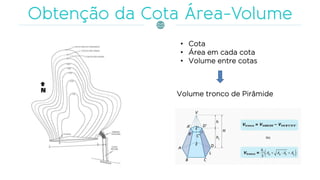
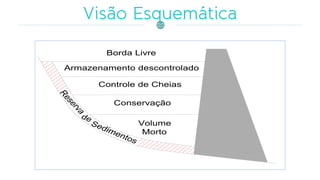
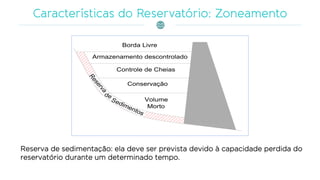
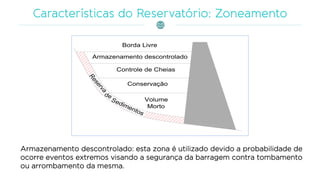
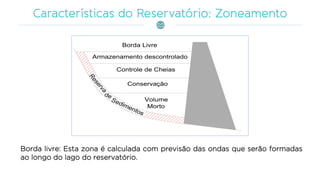
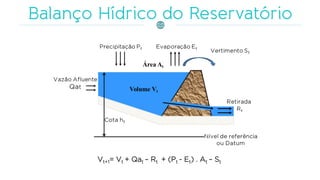
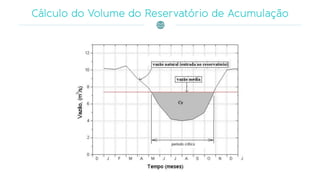
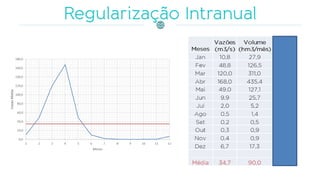
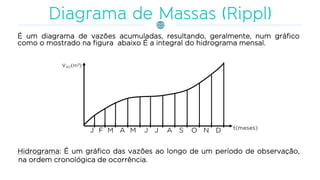
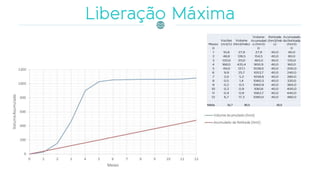
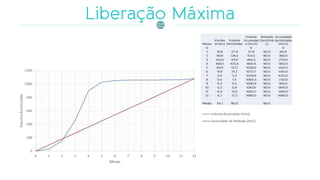
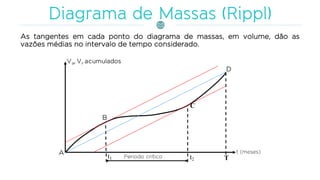
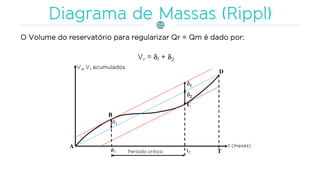
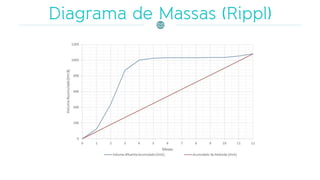
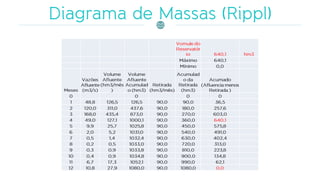
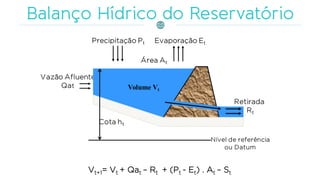
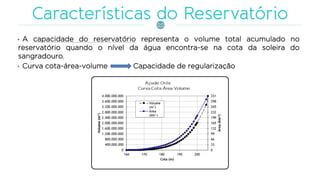
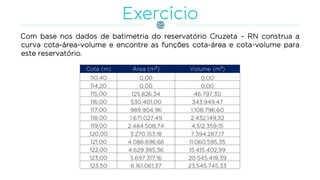
O documento discute a gestão de reservatórios, abordando aspectos técnicos como vazões afluentes, volume morto e controle de cheias. Também explora métodos de dimensionamento, incluindo empíricos, analíticos e experimentais, com foco na simulação do balanço hídrico. Por fim, menciona a necessidade de cálculo preciso para garantir o atendimento da demanda hídrica em períodos críticos.

1. Francisco de Assis de Souza Filho

3. Qmed =34,7 m3/s
Vazões Médias Mensais Afluentes ao Reservatório Orós

4. Regularização Interanual

5. Vazões Médias Anuais Afluentes ao Reservatório Orós

6. • Regularização Plurianual
• Regularização Interanual
• Reservatório de Compensação (diária, horária)
Escala de Tempo da Regularização

12. • Cota
• Área em cada cota
• Volume entre cotas
Volume tronco de Pirâmide

16. Reserva
de
Sedimentos
Volume
Morto
Conservação
Controle de Cheias
Armazenamento descontrolado
Borda Livre

17. Reserva
de
Sedimentos
Volume
Morto
Conservação
Controle de Cheias
Armazenamento descontrolado
Borda Livre
Reserva de sedimentação: ela deve ser prevista devido à capacidade perdida do
reservatório durante um determinado tempo.

18. Reserva
de
Sedimentos
Volume
Morto
Conservação
Controle de Cheias
Armazenamento descontrolado
Borda Livre
Volume morto: é o volume mínimo necessário de um reservatório para que se
possa garantir a sobrevivência dos seres que no mesmo habitam.

19. Reserva
de
Sedimentos
Volume
Morto
Conservação
Controle de Cheias
Armazenamento descontrolado
Borda Livre
Zona de conservação: é a zona que ficará armazenamento o volume necessário
para atender aos múltiplos usos.

20. Reserva
de
Sedimentos
Volume
Morto
Conservação
Controle de Cheias
Armazenamento descontrolado
Borda Livre
Controle de cheias: esta área deve permanecer vazia, exceto durante e
imediatamente depois de um evento de inundação.

21. Reserva
de
Sedimentos
Volume
Morto
Conservação
Controle de Cheias
Armazenamento descontrolado
Borda Livre
Armazenamento descontrolado: esta zona é utilizado devido a probabilidade de
ocorre eventos extremos visando a segurança da barragem contra tombamento
ou arrombamento da mesma.

22. Reserva
de
Sedimentos
Volume
Morto
Conservação
Controle de Cheias
Armazenamento descontrolado
Borda Livre
Borda livre: Esta zona é calculada com previsão das ondas que serão formadas
ao longo do lago do reservatório.

23. Barramento & Lago
• Barramento
- Concreto
- Terra
• Vertedouro
• Tomada d’água
• Diques auxiliares

24. Os vertedores são o principal tipo de estrutura de saída de água. Destinam-se
a liberar o excesso de água que não pode ser aproveitado pela demanda. Eles
são dimensionados para permitir a passagem de uma cheia rara (alto tempo de
retorno) com segurança.

27. Vt+1= Vt + Qat – Rt + (Pt - Et) . At – St

28. Equação da continuidade:
Em termos de taxas instantâneas:
Onde:
• Vt e Vt+t denotam o volume armazenado no inicio e no final em um intervalo
de tempo;
• I é o volume de entrada;
• O é o volume de saída;
• dV/dt denota a mudança do volume de armazenamento (V) com relação ao
tempo (t)

29. • Equação de Balanço Hídrico  Simulação
ttttttΔtt QvEDIPSS 
Somente ocorre se St+∆t > Vmáx
Desconsiderando a precipitação e a evaporação:
ttttΔtt QvDISS 

31. Vt+1= Vt + Qat – Rt + (Pt - Et) . At – St

34. É um diagrama de vazões acumuladas, resultando, geralmente, num gráfico
como o mostrado na figura abaixo É a integral do hidrograma mensal.
Hidrograma: É um gráfico das vazões ao longo de um período de observação,
na ordem cronológica de ocorrência.

39. As tangentes em cada ponto do diagrama de massas, em volume, dão as
vazões médias no intervalo de tempo considerado.

40. O Volume do reservatório para regularizar Qr = Qm é dado por:

45. Vt+1= Vt + Qat – Rt + (Pt - Et) . At – St

47. Diagrama de regularização. (Fonte. CAMPOS, 1990).

48. Devido ao grande número de variáveis estima-se alguns parâmetros nos
adimensionais:
fk =

K
Fator adimensional de capacidade
fM =

M
Fator adimensional de retirada
fE =
1/3
E1/33 v


Fator adimensional de evaporação
Assim, a equação descrita no slide anterior fica simplificada:
PE = f (fE, CV, PI, fk, fM)

49. Operação Simulada do Reservatório
✓Realizada através da solução da equação do balanço hídrico do reservatório
através de processo de integração numérica.

50. ✓O uso do diagrama triangular é restrito aos caso em que se pretende uma
garantia de 90% de fornecimento de água.

52. 1. Introdução
2. Características do reservatório
3. Cálculo do volume do reservatório de acumulação: lei de regularização
4. Balanço hídrico do reservatório
5. Dimensionamento de reservatório
6.1. Diagrama de Rippl
6.2. Método Analítico
6.3. Método Experimental

53. Regularização de Vazões

54. Um reservatório pode ser descrito por seus
níveis e volumes característicos, como o
volume morto e o volume máximo.
Outras características importantes são as
estruturas de saída de água, eclusas para
navegação, tomadas de água para irrigação
ou para abastecimento, e eventuais
estruturas de aproveitamento para lazer e
recreação.

55. • A capacidade do reservatório representa o volume total acumulado no
reservatório quando o nível da água encontra-se na cota da soleira do
sangradouro.
• Curva cota-área-volume Capacidade de regularização

56. Com base nos dados de batimetria do reservatório Cruzeta – RN construa a
curva cota-área-volume e encontre as funções cota-área e cota-volume para
este reservatório.

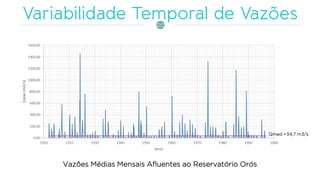
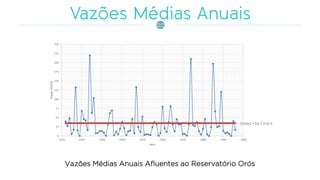
57. Costuma-se chamar de lei de regularização a função:
m
r
Q
tQ
ty
)(
)(  y(t) ≤1
Onde:
Qr (t) = vazão de regularização =  Qdemanda
Qm = vazão média = (1/n). Qnaturais, para n = no de meses
Conhecidas as vazões naturais [Qi(t)] e a lei de regularização y(t), a vazão Qr e
a capacidade mínima do reservatório podem ser determinadas.

58. •A máxima vazão que pode ser regularizada é a vazão média da bacia ou y(t) = 1.
•Suponha que as vazões naturais fossem acumuladas no tempo N (figura abaixo).

59. •A tangente do ângulo  é a vazão média
tg() = Qa / N = Qm
Se Qr > Qm então o reservatório
não vai atender a demanda total
todo o tempo porque Qr > Qa

60. ✓A capacidade mínima (Cr) de um reservatório para atender a uma dada lei de
regularização é obtida pela diferença entre o volume acumulado necessário
para atender àquela lei no período mais crítico de estiagem (Vnec) e o volume
acumulado que aflui ao reservatório no mesmo período (Vaf).

62. Método gráfico
Se demanda = vazão média  Capacidade = Vaf - VQmed
VQmed
Capacidade

63. Vt+1= Vt + Qat – Rt + (Pt - Et) . At – St

64. O dimensionamento de reservatórios pode ser feito com base na equação
abaixo:
Em que as entrada (I) serão as vazões afluentes, as saídas (O) as demandas e o
Vmáx será o volume útil do reservatório.

65. Métodos:
• Empíricos - relacionados ao estudo de períodos críticos da série histórica
através, por exemplo, do diagrama Rippl.
• Analíticos - são aqueles que seguem a teoria dos "Range", Teoria das Filas, ou
teoria das Matrizes de Transição (Teoria de Moran).
• Experimental - (Método Monte Carlo) Consiste na geração de séries sintéticas
de deflúvio e posterior operação simulada do reservatório.

66. Supondo que y(t) = 1 ou Qr = Qm, pode-se ver que as retiradas acumuladas de
B a C são maiores que as afluências, deplecionando o reservatório no período.

67. Desse modo, os pontos B e C são críticos e podem ser utilizados para definir a
capacidade do reservatório.

68. O Volume do reservatório para regularizar Qr = Qm é dado por:
Vr = 1 + 2

69. Utilizando o diagrama de Rippl e com base nos
dados de vazões mostrados, qual o volume que
deve ter o reservatório para atender uma vazão
de regularização igual a vazão média da bacia?

70. O método busca a solução da equação:
PE = probabilidade do reservatório esvaziar em um dada ano
K = capacidade do reservatório
Cv = coeficiente de variação dos deflúvios anuais
= valor médio dos deflúvios anuais
PJ = probabilidade de um ano ser totalmente seco
Ev = a lâmina evaporada do reservatório durante a estação seca
= fator de forma da bacia hidráulica obtido supondo que a relação cota
volume é do tipo V = h³
m = retirada anual do reservatório para fins utilitários
PE = f (K, CV, , PJ, Ev , , m)

71. O uso de método experimental no dimensionamento de reservatório consiste
na geração de séries sintéticas e posterior operação simulada do reservatório
através de um modelo.
1. Geração Sintética de Deflúvios
✓Os deflúvios anuais podem ser considerados serialmente independentes;
✓ As séries podem ser obtidas através da geração de números aleatórios
seguindo uma dada função densidade de probabilidade;
✓Utiliza-se a distribuição Gama para representar os deflúvios anuais (os
parâmetros estatísticos da série histórica são conservados).

72. Determinar a menor capacidade
útil de um reservatório suficiente
para atender a maior demanda
(vazão máxima regularizável)
• Equação de Balanço Hídrico  Simulação
QI
t
S




73. Capacidade mínima  diferença entre o volume acumulado que seria
necessário para atender à demanda, no período mais crítico de estiagem e o
volume acumulado que aflui ao reservatório no mesmo período
Método gráfico
Dos vários períodos de estiagem, o mais
crítico é aquele que resulta na capacidade do
reservatório  calcula-se esta para os
períodos de estiagem e se escolhe o maior
valor calculado

74. Método gráfico
Se demanda = vazão média  Capacidade = Vaf - VQmed
VQmed
Capacidade

75. Método gráfico
Supondo que a única saída é por descargas operadas, desprezando a
evaporação e a infiltração

76. • Equação de Balanço Hídrico  Simulação
ttttttΔtt QvEDIPSS 
ttttΔtt QvDISS 
Desconsiderando a precipitação e a evaporação:
Somente ocorre se St+∆t > Vmáx

77. Problema: dimensionar um reservatório com o volume necessário para
regularizar uma vazão D (constante ou variável)
ttttΔtt QvDISS Passos:
1.Estime um valor de Vmax
2. Em um mês qualquer, se St+t for menor que zero, a demanda Dt deve ser
reduzida até que St+t seja igual a zero, e é computada uma falha de
entendimento

78. Quanto à vazão disponível  desejável que a série tenha várias décadas.
Quanto à demanda D  pode variar com a época do ano.
ttttΔtt QvDISS 
3. Calcule a probabilidade de falha dividindo o número de meses com falha
pelo número total de meses. Se esta probabilidade for considerada inaceitável,
aumente o valor do volume máximo Vmax e reinicie o processo.