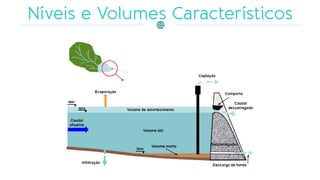
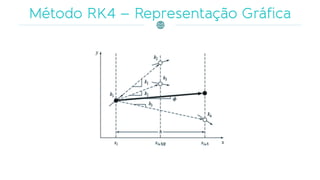
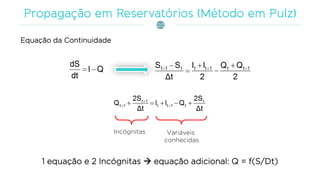
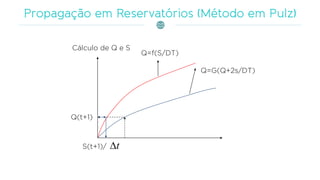
Os reservatórios são projetados para acumular água durante períodos chuvosos, compensando a escassez durante estiagens e regulando as vazões naturais. O documento discute métodos matemáticos, como a modelação da propagação de cheias e o uso do método de Runge-Kutta, para descrever o comportamento hidrológico, respeitando relações entre caudais e armazenamento. Também aborda a caracterização dos reservatórios por níveis e volumes operacionais, e as equações utilizadas em sua modelagem.

1. Francisco de Assis de Souza Filho

2. Os reservatórios tem por objetivo acumular parte das águas disponíveis nos
períodos chuvosos para compensar as deficiências nos períodos de estiagem,
exercendo um efeito regularizador das vazões naturais.

3. Em geral os reservatórios são formados por meio de barragens implantadas nos
cursos d‘água. Suas características físicas, especialmente a capacidade de
armazenamento, dependem das características topográficas do vale em que
estão inseridos.

4. Propagação: procedimento matemático para determinar a variação da
magnitude, da velocidade e da forma de uma onda de cheia, em função do
tempo, num ou mais pontos de um curso de água ou de um reservatório.
•Modelação simples, mas com alguma base física.
•Recorre à equação da continuidade e a uma equação para
caracterizar o armazenamento de água no rio ou reservatório.
•Modela a variação temporal da Vazão num determinado ponto.
•Modelação normalmente agregada.
• Modelação com base física.
• Recorre à equação da continuidade e da conservação da quantidade de
movimento.
• O escoamento variável é normalmente considerado a uma dimensão (ao longo
do curso de água ou do reservatório), o que conduz às equações de Saint-Venant
• Modela simultaneamente a variação temporal da vazão e da altura da água em
diferentes pontos do espaço.
• Modelação normalmente distribuída.

5. Um reservatório pode ser descrito por seus níveis e volumes característicos:
▪ Nível mínimo operacional
▪ Nível máximo operacional
▪ Volume máximo
▪ Volume morto
▪ Volume útil

7. Equação da continuidade:
QI
t
S



Intervalo de tempo curto: cheias
Intervalo de tempo longo: dimensionamento
Métodos gráficos
(antigos)
Simulação

8. Dados os hidrogramas de entrada no reservatório, qI(t), e de saída deste, qo(t),
representados na Figura, a forma diferencial da equação da continuidade é:
Em que S representa o armazenamento no reservatório.
A caracterização do sistema fica completa se se conhecer a relação S= f(qo). Esta relação
não se conhece normalmente de uma forma analítica, mas sim de uma forma tabular.

9. A relação entre o caudal de saída e o
armazenamento pode ser variável ou constante.
Relação constante:
• Reservatório com superfície horizontal
(larga e profunda, com reduzidas velocidades)
• Há uma descarga fixa para uma dada carga
h: S = f(qo)
• O armazenamento máximo ocorre
quando os hidrogramas se cruzam, isto é,
quando:
• Como S = f(qo), então ao máximo
armazenamento, Sm, corresponde o vazão máxima de saída, qOp.

11. O Método RK4 pode ser utilizado como alternativa ao Método de Plus na
modelagem de propagação de cheias e dimensionamento de vertedouros em
reservatórios.
A equação utilizada na propagação de cheias é:
V é o volume da água no reservatório;
I é vazão afluente ao reservatório devido à
precipitação;
Q é a vazão efluente devido ao vertimento;
L é o comprimento do vertedouro;
H é a cota do nível da água em acima da
cota do vertedouro;
y e C são coeficientes.

12. Esta equação pode ser resolvida pelo RK4 considerando variações nas vazões
durante o intervalo modelado, ao adotar:
A vazão afluente como função do tempo I(t);
A vazão efluente como função do volume de água no reservatório Q(V), Uma
vez que H é função de V e é calculado pela CAV do reservatório;
Assim, as equações tornam-se:
A resolução da Propagação de Cheias, pelo método RK4, considerando I(t)
linear em função do tempo, estão apresentadas na planilha.

13. Os métodos de Runge-Kutta (RK) utilizam a extrapolação linear:
Onde,
yi+1 é o valor de y no final do intervalo;
yi é o valor de y no início do intervalo;
é o valor estimado da inclinação para o intervalo;
h é o tamanho do intervalo.
Para a resolução das equações diferenciais ordinárias de forma:

14. - Os métodos RK estimam o valor da inclinação (Ø) utilizada na extrapolação
linear a partir do valor da equação diferencial (dy/dx) no ponto inicial do
intervalo.
- Assim, a utilização dos métodos RK necessita dos valores da função e da
equação diferencial no ponto inicial como condições de contorno.
- Dentre os métodos RK, se destacam o de Euler, o de Heun e os de Quarta
Ordem.

15. É o método RK mais utilizado.
O método RK4 determina a inclinação da extrapolação linear a partir de 4 estimativas EDO (derivada) no
intervalo.
O método RK4 é dado por:
Ou seja:
Onde
- k1 é o valor da equação diferencial no início do intervalo;
- k2 é o valor da equação diferencial na metade do intervalo, no ponto estimado pela extrapolação linear de
inclinação k1;
- k3 é o valor da diferencial na metade do intervalo, no ponto estimado pela extrapolação linear de
inclinação k2;
- k4 é o valor da diferencial no final do intervalo, no ponto estimado pela extrapolação linear de inclinação
k3.

18. Considerando um reservatório com vertedor livre, em que a vazão de saída é
uma função do nível da água no reservatório, a equação abaixo pode ser
aplicada recursivamente.
2
QQ
2
II
t
SS ttttttttt  





Nesta equação, em cada intervalo de tempo são conhecidas as vazões de entrada
no tempo t e em t+t; a vazão de saída no intervalo de tempo t; e o volume
armazenado no intervalo t. Não são conhecidos os termos St+t e Qt+t , e
ambos dependem do nível da água.
Como tanto St+t e Qt+t são funções não lineares de ht +t , a equação de
balanço pode ser resolvida utilizando a técnica iterativa de Newton, ou ‘outro
método numérico.

19. Uma forma mais simples de calcular a propagação de vazão num reservatório
é o método conhecido como Puls modificado. Neste método a equação acima
é reescrita como:
t
t
ttttt
tt
Q
t
S2
IIQ
t
S2








Uma tabela da relação entre Qt+t e 2.(St+t )/t pode ser gerada a partir da
relação cota – área – volume do reservatório e através da relação entre a cota
e a vazão, por exemplo para uma equação de vertedor.
t
t
ttttt
tt
Q
t
S2
IIQ
t
S2









20. Equação da Continuidade
Incógnitas Variáveis
conhecidas
1 equação e 2 Incógnitas  equação adicional: Q = f(S/Dt)

21. Cálculo de Q e S
Q=f(S/DT)
Q=G(Q+2s/DT)
Q(t+1)
S(t+1)/ t

22. Função auxiliarQ = f(S/Dt) Q = f1(Q + 2.S/Dt)
Construídas a partir da curva cota x S e cota x Q saída pelas estruturas hidráulicas

23. Metodologia
1. Estabeleça as condições iniciais So (volume inicial)  calcular;
Q0 = f(S0/Dt) no gráfico Q = f(S/Dt);
2. Calcule o valor G = lado direito da equação acima;
3. Este valor é igual a f1 = lado esquerdo da equação acima;
4. No gráfico Q = f1(Q + 2.S/Dt)  determinar Qt+1 e St+1
5. Repete-se os itens 2 a 4 até o último intervalo de tempo.

24. Metodologia
Δt
2S
QII
Δt
2S
Q t
t1tt
1t
1t  


Q=f(S/DT) Q=f1(Q+2S/DT)
Qt+1
Cálculo de G com o hidrograma
de entrada
St+1/Dt