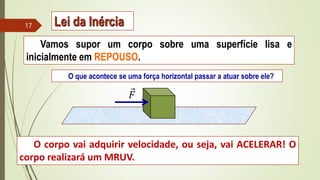
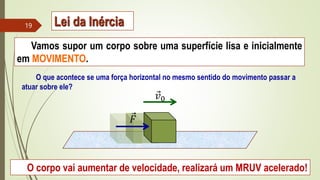
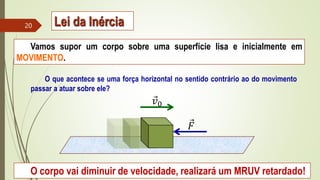
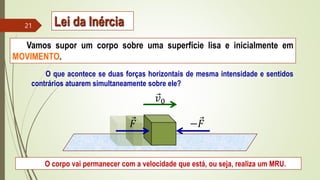
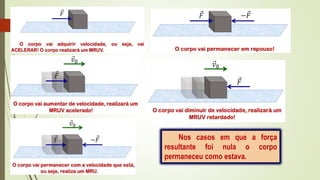
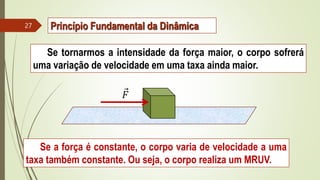
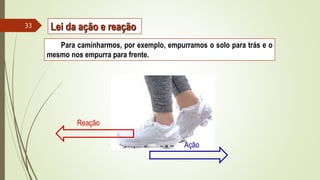
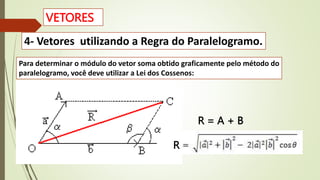
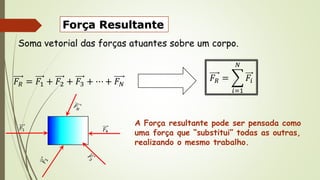
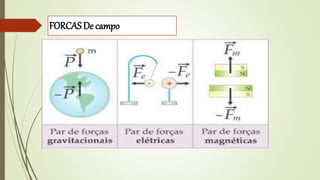
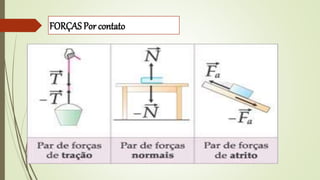
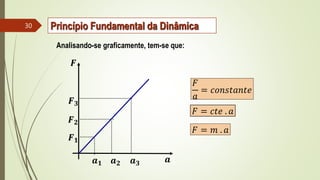
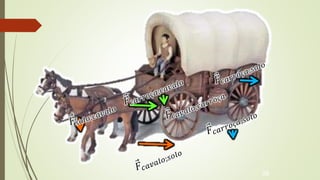
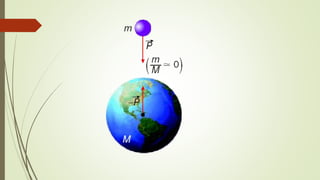
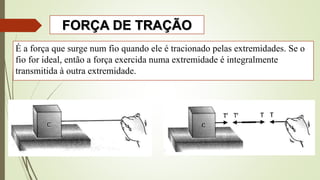
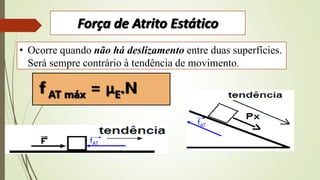
O documento resume conceitos fundamentais de dinâmica e forças, incluindo: 1) As três leis de Newton sobre forças e movimento. 2) Conceitos de força resultante, peso, força normal, força elástica e atrito. 3) Exemplos ilustrativos sobre como estas leis se aplicam em situações cotidianas.

1. Aulão Enem - Física
Prof.: Daniela Braz
Dinâmica

2. ORIGEM EXTREMIDADE
VETORES

3. 1- Vetores na mesma direção e sentido.
VETORES

4. 2- Vetores na mesma direção e sentidos contrários.
VETORES

5. 3- Vetores perpendiculares (90°) entre si.
VETORES

6. VETORES
4- Vetores utilizando a Regra do Paralelogramo.
A regra é posicionar a origem dos dois vetores no mesmo ponto e traçar uma reta
paralela a cada um passando pela extremidade do outro.
a sua soma é igual ao vetor que
corresponde à diagonal do
paralelogramo e que começa no
mesmo ponto dos vetores.

7. VETORES
4- Vetores utilizando a Regra do Paralelogramo.
R = A + B
Para determinar o módulo do vetor soma obtido graficamente pelo método do
paralelogramo, você deve utilizar a Lei dos Cossenos:
R

8. Exemplo
8
Verifique quais são as grandezas escalares e vetoriais nas afirmações abaixo.
1) O deslocamento de um avião foi de 100 km, na direção Norte do Brasil.
2) A área da residência a ser construída é de 120,00 m2.
3) A força necessária para colocar uma caixa de 10 kg em uma prateleira é de 100 N.
4) A velocidade marcada no velocímetro de um automóvel é de 80 km/h.
5) Um jogo de futebol tem um tempo de duração de 90 minutos.
Assinale a alternativa que apresenta a sequência correta.
a) vetorial, vetorial, escalar, vetorial, escalar.
b) vetorial, escalar, escalar, vetorial, escalar.
c) escalar, escalar, vetorial, vetorial, escalar.
d) vetorial, escalar, vetorial, vetorial, escalar.
e) escalar, escalar, vetorial, escalar, escalar.

9. Exercício
Considere dois vetores deslocamento, de módulos a e b, que
são perpendiculares entre si. Sabendo-se que a = 8 cm e que
o vetor resultante da soma dos dois vetores possui módulo
igual a 10 cm, o módulo do vetor b é igual a:
a)2 cm
b)6 cm
c)10 cm
d)18 cm
e)36 cm

10. Para responder a essa pergunta basta saber alguns conceitos
de resultante de vetores.
Se os vetores estão perpendiculares entre si, a sua resultante
representa a hipotenusa de um triângulo retângulo, cuja
hipotenusa será 10, um cateto será de 8. Para saber o F2 basta
colocar no teorema de Pitágoras. Assim:
Logo, o vetor F2 mede 6cm. Sendo a resposta certa a letra A.

11. DINÂMICA
FORÇAS, LEIS DE NEWTON, TRABALHO E ENERGIA

12. Efeitos da Força
Como a força é quem altera o estado de um corpo,
os seus possíveis efeitos são causar:
1- Deformação;
2- Alteração da Velocidade, gerando aceleração;
3- Equilíbrio.

13. Força Resultante
Soma vetorial das forças atuantes sobre um corpo.
𝐹𝑅 = 𝐹1 + 𝐹2 + 𝐹3 + ⋯ + 𝐹𝑁
𝐹𝑅 =
𝑖=1
𝑁
𝐹𝑖
𝐹1 𝐹4
A Força resultante pode ser pensada como
uma força que “substitui” todas as outras,
realizando o mesmo trabalho.

14. FORCAS De campo

15. FORÇAS Por contato

16. 1ª Lei de Newton – Lei da Inércia
“Qualquer corpo tende a permanecer em seu estado de
movimento ou de repouso se a resultante das forças que
atuam sobre ele for nula.”
0

R
F

→ REPOUSO ou MRU

17. Vamos supor um corpo sobre uma superfície lisa e
inicialmente em REPOUSO.
O que acontece se uma força horizontal passar a atuar sobre ele?
O corpo vai adquirir velocidade, ou seja, vai ACELERAR! O
corpo realizará um MRUV.
𝐹
Lei da Inércia
17

18. Vamos supor um corpo sobre uma superfície lisa e
inicialmente em REPOUSO.
O que acontece se duas forças horizontais de mesma intensidade e sentidos
contrários atuarem simultaneamente sobre ele?
O corpo vai permanecer em repouso!
𝐹 −𝐹
18 Lei da Inércia

19. Vamos supor um corpo sobre uma superfície lisa e inicialmente
em MOVIMENTO.
O que acontece se uma força horizontal no mesmo sentido do movimento passar a
atuar sobre ele?
O corpo vai aumentar de velocidade, realizará um MRUV acelerado!
𝐹
𝑣0
19 Lei da Inércia

20. Vamos supor um corpo sobre uma superfície lisa e inicialmente em
MOVIMENTO.
O que acontece se uma força horizontal no sentido contrário ao do movimento
passar a atuar sobre ele?
O corpo vai diminuir de velocidade, realizará um MRUV retardado!
𝐹
𝑣0
20 Lei da Inércia

21. Vamos supor um corpo sobre uma superfície lisa e inicialmente em
MOVIMENTO.
O que acontece se duas forças horizontais de mesma intensidade e sentidos
contrários atuarem simultaneamente sobre ele?
O corpo vai permanecer com a velocidade que está, ou seja, realiza um MRU.
𝑣0
𝐹 −𝐹
21 Lei da Inércia

22. Nos casos em que a força
resultante foi nula o corpo
permaneceu como estava.
22

23. • Assim, conclui-se que a matéria possui uma tendência
natural de permanecer como está, ou seja, de resistir à
mudança de velocidade.
• A essa tendência natural foi dado o nome de INÉRCIA.
• A inércia de um corpo é proporcional à sua massa. Assim
pode-se considerar a massa como a medida da inércia de
um corpo.
23 Lei da Inércia

25. 2ª Lei de Newton – Lei Fundamental da Dinâmica
“A Força Resultante sobre um corpo é igual ao produto da
sua massa pela aceleração que adquire.”
a
m
FR


.


26. Vamos considerar um caso em que uma força
resultante diferente de zero atua sobre um corpo:
O que ocorre com a velocidade do corpo?
Se a força é constante, o corpo varia de velocidade a uma
taxa também constante. Ou seja, o corpo realiza um MRUV.
𝐹
Princípio Fundamental da Dinâmica
26

27. Se tornarmos a intensidade da força maior, o corpo sofrerá
uma variação de velocidade em uma taxa ainda maior.
Se a força é constante, o corpo varia de velocidade a uma
taxa também constante. Ou seja, o corpo realiza um MRUV.
𝐹
27 Princípio Fundamental da Dinâmica

28. Observa-se também uma variação na aceleração adquirida
quando se varia a massa do corpo a ser submetido a ação da
força:
Neste caso o corpo varia de velocidade mais rapidamente.
𝐹
28 Princípio Fundamental da Dinâmica

29. Assim, pode-se concluir que:
Um corpo submetido a uma força resultante
diferente de zero adquire uma aceleração
inversamente proporcional à sua massa.
29 Princípio Fundamental da Dinâmica

30. Analisando-se graficamente, tem-se que:
𝑭
𝒂
𝑭𝟏
𝑭𝟐
𝑭𝟑
𝒂𝟏 𝒂𝟐 𝒂𝟑
𝐹
𝑎
= 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒
𝐹 = 𝑐𝑡𝑒 . 𝑎
𝐹 = 𝑚 . 𝑎
30 Princípio Fundamental da Dinâmica

31. Dessa forma, enuncia-se que:
𝐹𝑅 = 𝑚 . 𝑎
Note que:
• O vetor 𝑎 aponta na mesma direção do vetor 𝐹𝑅;
• Se 𝑎 aponta na mesma direção e sentido do vetor velocidade, o movimento é
acelerado. Caso o contrário o movimento é retardado.
31 Princípio Fundamental da Dinâmica
• No sistema internacional a força é dada em Newton (N).
1𝑁 = 1𝑘𝑔. 𝑚/𝑠2

32. 3ª Lei de Newton – Lei da Ação e Reação
“A toda ação corresponde uma reação, de mesma intensidade,
mesma direção, porém de sentido contrário atuando em
corpos distintos.”
21
12 F
F





33. Para caminharmos, por exemplo, empurramos o solo para trás e o
mesmo nos empurra para frente.
Ação
Reação
Lei da ação e reação
33

34. 34 Lei da ação e reação

35. Foguete
expelindo os
gases (ação)
Gases
empurrando o
foguete (Reação)
35 Lei da ação e reação

36. • A ação e a reação atuam em corpos distintos e, portanto,
não podemos dizer que elas se cancelam.
• A ação e a reação apresentam mesmo módulo, mesma
direção e sentidos contrários. Mas, as acelerações
adquiridas pelos corpos dependem das suas massas.
36 Lei da ação e reação

37. Se a carroça puxa o burro com a mesma
intensidade e sentido contrário ao da força
que o burro exerce nela, como eles podem
se mover?
37

38. 38

39. 1) As forças de ação e reação aparecem aos pares, sempre
que dois corpos interagem;
2) Os pares ação/reação podem ser de contato direto ou de
ação a distância sendo o par sempre da mesma natureza;
3) Os pares ação/reação nunca se anulam pois atuam em
corpos diferentes.
Lei da ação e reação

40. Newton postulou que todo corpo dotado de massa atrai outros
corpos que também tenham massa. Essa força de atração é
conhecida como força gravitacional. Todos os corpos na
superfície da Terra são atraídos na direção do centro do nosso
planeta com uma força que chamamos de PESO.
g
m
P


.

g vale aproximadamente
10 m/s² na superfície da Terra.
FORÇA PESO )
(P


42. EXEMPLOS
O uso do cinto de segurança pode evitar tanto acidentes graves quanto mortes. Com base
nas três leis de Newton, dentro do campo da Física, podemos explicar seu uso da seguinte
forma:
a) Considerando a massa (m) do cinto de segurança, podemos entender seu mecanismo baseado
na 2ª lei de Newton, pois devido à desaceleração (a) do carro o cinto exercerá uma força sobre
nosso corpo dada por: F = ma.
b) O cinto de segurança pode ser entendido como um dispositivo usado para diminuir a
aceleração do carro, portanto, está relacionado com a 2ª lei de Newton.
c) O cinto de segurança é um dispositivo baseado na 3ª lei de Newton, pois o carro exerce uma
força sobre o cinto e este reage, exercendo uma força sobre nosso corpo.
d) O cinto de segurança é um dispositivo usado para neutralizar a lei da inércia, evitando que
nosso corpo continue deslocando-se para frente, quando o carro diminui sua velocidade
bruscamente.

43. Certo carro nacional demora 30 s para acelerar de 0 a 108 km/h. Supondo sua
massa igual a 1200 kg, o módulo da força resultante que atua no veículo
durante esse intervalo de tempo é, em Newton, igual a:
a) zero.
b) 1200
c) 3600
d) 4320
e) 36000
EXEMPLOS

44. Observe a tira:
A forma encontrada por Garfield para perder peso é:
a) correta, uma vez que, em um planeta de gravidade menor, seu peso será realmente menor,
porém com a mesma massa.
b) errada, pois em um planeta de gravidade menor sua massa será maior, porém com o
mesmo peso.
c) correta, pois em um planeta de gravidade menor sua massa será menor, porém seu peso
será maior.
d) correta, pois em um planeta de gravidade menor sua massa e seu peso serão maiores.
e) correta, pois em um planeta de gravidade menor sua massa e seu peso serão menores.
EXEMPLOS

45. Surge quando um corpo se encontra
sobre certa superfície de apoio. A força
peso e a normal não formam um par
ação e reação.
Força Normal

46. É a força de reação que a superfície exerce sobre o corpo que a
comprime. É necessário a presença de uma superfície, e nem sempre
é igual ao peso do corpo.
Força Normal
O valor da Força Normal é igual ao da Força Peso quando a
superfície for perfeitamente perpendicular ao campo gravitacional
(horizontal) e não houverem outras forças atuando na mesma direção
da Força Peso.

47. FORÇA DE TRAÇÃO
É a força que surge num fio quando ele é tracionado pelas extremidades. Se o
fio for ideal, então a força exercida numa extremidade é integralmente
transmitida à outra extremidade.

48. FORÇA ELÁSTICA
Força que surge quando um corpo
interage com uma mola,
comprimindo-a ou distendendo-a.

49. LEI DE HOOK
Relaciona a deformação sofrida por uma
mola com a força nela aplicada e a sua
natureza, expressa pela chamada constante
elástica da mola.
F = k.x
elástica

50. x→ deformação da mola (m)
k → constante elástica da mola
(N/m)
F → Força aplicada (N)
F = k.x
elástica

51. Força de Atrito Estático
• Ocorre quando não há deslizamento entre duas superfícies.
Será sempre contrário à tendência de movimento.
fAT
fAT
f AT máx = μE.N

52. FORÇA DE ATRITO CINÉTICO
• Ocorre quando houver deslizamento entre duas superfícies. Será
sempre contrário ao movimento. Também chamado atrito
dinâmico.
A força de atrito cinético é dada por
N→ Força normal
μc→ Coeficiente de atrito cinético.
Depende das duas superfícies em contato.
fAT = μc.N

53. O atrito entre os pneus dos carros e o solo permite-lhes acelerar,
travar e parar.
O atrito entre os sapatos e o chão permite-nos andar.
O atrito entre os objetos e as mãos permite segurá-los.
O atrito entre a borracha e o papel permite apagar os riscos do lápis.
O atrito entre o giz e o quadro permite escrever.
ATRITO ÚTIL
ATRITO PREJUDUCIAL
- O atrito entre os móveis e o chão dificulta o seu movimento.
- O atrito entre as peças de uma máquina provoca o seu desgaste.

54. Macetes para resolução de problemas
1. Faça um esquema/desenho simples da situação.
3. Isole os corpos e faça um diagrama das forças atuantes em cada corpo.
2. Escolha um sistema de referência (sistema de coordenadas x,y).
Lembre-se de que:
• Se o corpo tem massa, existirá uma Força Peso. P = mg
• Se o corpo está em contato com a superfície, terá uma Força
Normal perpendicular à superfície.
• Se existem fios puxando corpos, existirão Forças de Tração.