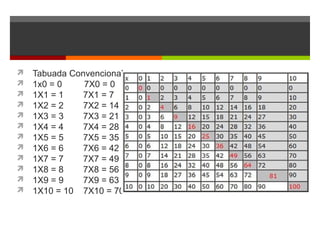
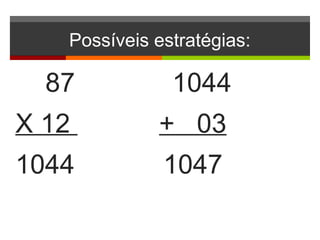
O documento discute conceitos básicos de matemática como adição, subtração, multiplicação e divisão. Inclui exemplos de como ensinar estas operações a crianças de forma lúdica e progressiva, utilizando atividades, jogos e a calculadora. Também aborda propriedades destas operações como comutatividade e distribuição.

1. 
Números & Operações

2. O que é a adição?
Adição é o agrupamento ou
soma de quantidades

3. Adição na escrita numérica
 A cálculo de sentença favorece o cálculo mental
 Exige que o aluno tenha um repertório mínimo de
operações mentais para realizar uma adição
 A grandeza do numeral faz diferença na exigência de
pensamento do sujeito
34 + 12 =

4. Adição na escrita númerica
 O cálculo armado reforça o uso do algoritmo e da
memória
 Ele é sempre um cálculo unitário, na medida em que
sempre é feita a soma de dois algarismos
 A grandeza do numeral é irrelevante

5. Adição na escrita numérica
 Como o cálculo armado favorece adições com
valores compostos de apenas 1 algarismo, o
problema surge quando a resposta tem um
valor representa com 2 algarismos
17
+ 18
2 15

8. Ensino precoce de algorítmos
 As crianças lidam com a multiplicação e divisão no dia a dia desde a
Educação Infantil, mas não reconhecem ainda como operações formais;
 As dificuldades com a operação começam quando aparece a conta
armada (algoritmo) - a estrutura dela não revela de modo claro outras
operações utilizadas durante o processo: a multiplicação e a subtração;
 É preciso, então, ir além do algoritmo, partir de problemas mais simples,
até os mais complexos e somente depois de consolidadas as noções
divisórias apresentar o algoritmo da divisão;
 Ao considerar os modos de resolução dos estudantes e apresentar
questões que envolvem mais que a resolução dos cálculos, a turma é
desafiada a explorar a quantidade global envolvida e não somente o valor
posicional dos números.

9. A PROPORÇÃO NA RELAÇÃO ENTRE OS NÚMEROS
 Numa tabuada os números são organizados de uma maneira
uniforme e sistemática. O resultado de 1X7, por exemplo, é
menor que o de 7X2, que é menor que o 7X7, e os valores
aumentam de 7 em 7. Isso se repete nas tabuada do 3, que
varia de 3 em 3, na do 4, de 4 em 4. Essa ideia se refere a
propriedade da multiplicação da proporcionalidade.
 Quando uma grandeza dobre e a outra também dobre, quando
uma triplica e a outra triplica, temos uma proporcionalidade
direta. Sem ter consciência dessa regularidade o aluno não
compreende a tabuada.
 *Atividade proposta, trabalho com fita métrica.

10. A tabela pitagórica é um quadro de
dupla entrada em que são registrados
os resultados das multiplicações, no
qual o número da linha deve ser
multiplicado pelo da coluna e no
espaço correspondente ao encontro
das duas, deve-se registrado o
resultado do cálculo.

11.  Tabuada Convencional
 1x0 = 0 7X0 = 0
 1X1 = 1 7X1 = 7
 1X2 = 2 7X2 = 14
 1X3 = 3 7X3 = 21
 1X4 = 4 7X4 = 28
 1X5 = 5 7X5 = 35
 1X6 = 6 7X6 = 42
 1X7 = 7 7X7 = 49
 1X8 = 8 7X8 = 56
 1X9 = 9 7X9 = 63
 1X10 = 10 7X10 = 70

12. ATIVIDADE PROPOSTA:

Uma moto tem 2 rodas, quantas rodas tem em 4 motos?

Um carro tem 4 rodas, quantas rodas tem em 2 carros?

13. PROPOSTA DO USO DA TABELA PITAGÓRICA
• Pode preencher somente as tabuadas do 5 e do 10 para
verificar que os resultados da primeira correspondem à
metade dos resultados da segunda.
• escrever os resultados do 2 e do 3 e concluir que a soma
dos produtos corresponde aos resultados da do 5.
• Dessa forma os alunos pode tirar diversas conclusões e ir
memorizando os valores ou encontrá-los com facilidade.
• Explorar as relações entre os dobros, os triplos e os
quádruplos na tabela é essencial.
• Serve também como material de consulta dos alunos .

14. Propriedade da Comutatividade
A comutatividade indica que a ordem dos fatores não altera o
produto.
Ex: 8X4 e em 4X8, os resultados serão os mesmo.
Atividade proposta:
Uma aranha tem 8 patas, quantas patas tem 4 aranhas?
Um cachorro tem 4 patas, quantas patas tem 8 cachorros?

15. PROPRIEDADE DISTRIBUTIVA
A soma dos números multiplicados por 2 e 5 está na coluna
do 7, assim como a soma dos multiplicados por 3 e 4. Essa
relação se baseia nas propriedades associativa e distributiva
da multiplicação. Matematicamente, 7 x 6 pode ter esta
representação
(3 x 6) + (4 x 6)
18 + 24 = 42

16. DIVISÃO
 Para começar a trabalhar com o algoritmo da divisão, as
outras operações já precisam estar bem apreendidas
pelas crianças e o sistema de numeração decimal deve
possuir significado para elas.
:
? | ?
- ? ? x

17.  Deve-se iniciar com problemas simples, como “quero
fazer equipes de 3 crianças com os alunos da turma, são
25 crianças, quantas equipes posso fazer?”.
 Alguns podem responder que podem fazer 8 equipes e
sobrará uma criança, outros podem já incluir esta criança
em alguma equipe, o que vale é observar as estratégias
das crianças.

18. Problemas que não fazem referência a
um contexto de distribuição:
"Tenho no banco R$1240, saco R$90 a cada
dia, durante quantos dias vou poder sacar
essa quantidade?"
"Estou lendo um livro e me propus a ler 15
páginas por dia. Se o livro tem 180 páginas,
quantos dias demorarei para terminá-lo?"

19. Problemas de "partição".
 Problemas em que se conhece a quantidade total, é
preciso reparti-la em uma quantidade conhecida de partes
iguais e se deve determinar quanto corresponde a cada
parte:
 "Juliana tem 20 balas e quer distribuí-las entre seus 5
amigos, de modo que todos comam a mesma quantidade.
Quantos caramelos dará para cada um?“;
 Problemas em que se tem uma quantidade total, se sabe
o que corresponde a cada parte e se deve determinar em
quantas partes é possível efetuar a distribuição:
 "Juliana tem 20 balas e quer dar 5 a cada um de seus 5
amigos. Para quantos amigos dará?".

20.  É preciso considerar que a divisão entre números naturais
nem sempre é exata;
 Dependendo do contexto e do tipo de pergunta do
problema, muitas vezes é necessário considerar o resto;
 Desde o início da escolaridade é possível propor às
crianças diversos problemas.

21.  É possível resolver um problema de divisão por meio de
diversas estratégias, desde desenhos ou esquema até
cálculos de adição, subtração e multiplicação.
 A melhor estratégia para resolver uma divisão é colocar
em jogo uma multiplicação;
 Desde os primeiros contatos com os problemas de repartir
e partir é necessário propor problemas às crianças que
deem resto 0 ou resto diferente de 0.

22. Problema com algoritmo: encontrar o
dividendo
? |12
3 87

23. Possíveis estratégias:
87 1044
X 12 + 03
1044 1047

24. Sem usar algorítmo:
 Num cinema há 375 poltronas. Se há 15
fileiras, quantas poltronas há por fileira?
 Podem usar desenho, escrita, qualquer
coisa, menos a “conta-armada”!
 Lembrando que é preciso anotar!

25. Com algorítmo:
Vinte pessoas foram a um restaurante
e gastaram ao todo R$1552,00. Eles
dividirão igualmente entre todos a
despesa, quanto deu pra cada um?

27. CALCULADORA
O trabalho com a calculadora contribui com o
raciocínio lógico-matemático das crianças
com relação ao sistema de numeração, à
compreensão das estratégias em contas de
adição e subtração e entendimento do valor
posicional, relacionados às unidades,
dezenas e centenas.

28. Nesta atividade serão utilizadas calculadoras como modo de pensar
diferentes estratégias para se chegar a um resultado. Entregaremos as
calculadoras e questionaremos para que serve e como se utiliza.
Escrever o numeral 13 no quadro e solicitar que eles transformem no
numeral 10. Explicar que nos próximos problemas serão propostos
desafios, em que eles devem transformar números em outros números,
sem poder utilizar algum algarismo da calculadora. Ao final de cada
resolução, solicitar que um dos grupos vá ao quadro explicar como
chegou ao resultado.
Então pedir que transformem o numeral 13 em uma dezena, sem
utilizar o algarismo 3, conforme exemplo:
 13 → 10 (sem usar nº 3): 13 + 2 – 5 = 10

29.  Mesmo que propostas curriculares ,amparadas em
pesquisas dentro da Educação Matemática, recomendem
o uso da calculadora, cabe ao (à) professor (a) a decisão
final de elaborar e propor aos seus alunos atividades com
recursos variados.
 Propõe –se que os alunos sejam auxiliados na exploração
do funcionamento da calculadora. Comentam-se sobre o
funcionamento das teclas.

30. 1ª atividade:
Complete, preenchendo o que falta:
153+ =255
330: =33
300=25 (utilizando a tecla de dividir e outras necessárias
durante o processo, sem usar a tecla do algarismo 2).
Quais teclas as crianças poderão pressionar?

31. Esta imagem traz um desafio que permite trabalhar com
conceitos básicos de matemática além de explorar o
funcionamento das calculadoras simples. Este nível de
dificuldade permite trabalhar com as operações de adição e
multiplicação e suas propriedades.

32.  25 → 27 (sem usar nº 2)
 15 → 9 (sem usar nº 6)
 29 → 20 (sem usar nº 9, 5, 4)
 31 → 25 (sem usar nº 6 e 3)
 48 → 12 (sem usar nº 36, 30, 10, 6)