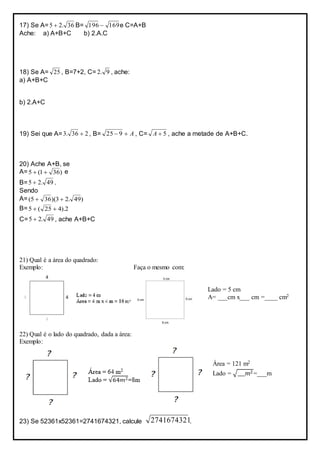
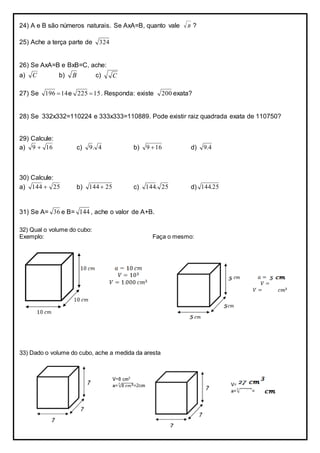
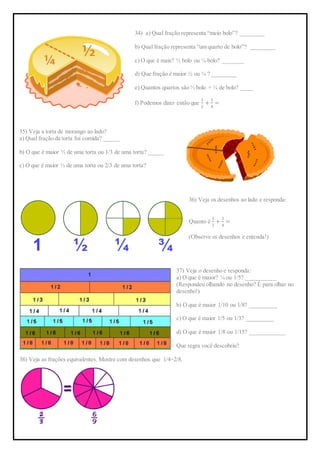
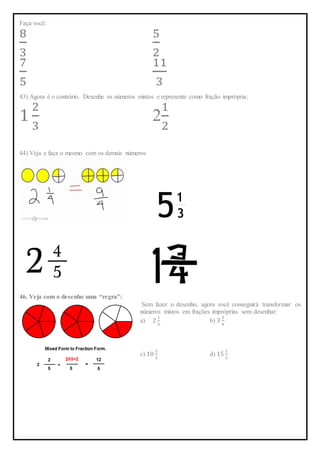
1. O documento é uma lista de exercícios de matemática sobre raízes quadradas, potenciação, frações e porcentagens para os alunos do 7o ano. 2. Os exercícios incluem cálculos numéricos, identificação e conversão entre frações equivalentes e mistas. 3. O professor encoraja os alunos a estudarem diariamente para se prepararem para a prova.

1. ESCOLA NOVA – MONTE SANTO DE MINAS – MG
Prof. Otávio Luciano Camargo Sales de Magalhães
7º Ano – 2016 – RESOLUÇÃO DE PROBLEMAS
17 DE MARÇO DE 2016
Nome: ________________________________________
Faça em aula e termine em casa
Estude 20 minutos por dia todo dia
REVISÃO DOS ASSUNTOS ABORDADOS DURANTE O BIMESTRE PARA A PROVA
Só se faz um bom futuro se esforçando! Estudem bastante, que vocês dão conta!
1. Calcule:
a)√36 b) √144 c) 32 d) 53
2. Calcule:
a) √36 + 52
b) √4900 c) √√81
3. Se
A=√49
B=23
Quanto vale A x B
4. Dado que A.A=B, quanto vale √ 𝐵
5. Calcule:
a) 105 b) 1152 c) 433
d) 150 e) 04000 f) 31
g) 50 h) 28 i) 35

2. 6) Calcule:
a) √25=________ b) √144=________ c) √100=________ d) 52
=________ e) 62
=________
f) 112
=________ g) √8
3
=________ h) √125
3
=________ i) 53
=________ j) 33
==________
7) Escreva-se como lê, seguindo os exemplos
52 – cinco ao quadrado 33 – três ao cubo
62=__________________ 73=__________________ 23=__________________
8) Qual é:
a) o dobro de 5______b) o quadrado de 5______c) o dobro de 10______d) o quadrado de 10______
e) o dobro de 7______f) o quadrado de 7______g) o dobro de 11______h) o quadrado de 11______
9) Qual é:
a) o triplo de 3______b) o cubo de 3______ c) o triplo de 5______ d) o cubo de 5______
e) o triplo de 7______ f) o cubo de 7______ g) o triplo de 10______ h) o quadrado de 10 ______
10) Continue a tabela:
6 . 6 . 6 = ____ ∴ √
3
= ____
7 . 7 . 7 = ____ ∴ √
3
= ____
8 . 8 . 8 = ____ ∴ √
3
= ____
9 . 9 . 9 = ____ ∴ √
3
= ____
10 . 10 . 10 = ____ ∴ √
3
= ____
11 . 11 . 11= ____ ∴ √
3
= ____
12 . 12 . 12 = ____ ∴ √
3
= ____
13 . 13 . 13 = ____ ∴ √
3
= ____
14 . 14 . 14 = ____ ∴ √
3
= ____
15 . 15 . 15 = ____ ∴ √
3
= ____
16 . 16 . 16 = ____ ∴ √
3
= ____
17 . 17 . 17 = ____ ∴ √
3
= ____
18 . 18 . 18 = ____ ∴ √
3
= ____
19 . 19 . 19 = ____ ∴ √
3
= ____
11) Veja!
14=1.1.1.1=1 ∴ √1
4
= 1
24=2.2.2.2=16 ∴ √16
4
= 2
34=3.3.3.3=81 ∴ √81
4
= 3
44=4.4.4.4=____ ∴ √_____4
= ____
54=5.5.5.5=____ ∴ √_____4
= ____
64=6.6.6.6=____ ∴ √_____4
= ____
74=7.7.7.7=____ ∴ √_____4
= ____
84=8.8.8.8=____ ∴ √_____4
= ____
94=9.9.9.9=____ ∴ √_____4
= ____
12) Calcule:
a) √125
3
=_____ b) √27
3
=_____ c) √81
4
=_____ d) √49=_____ e) √256
4
=_____
f) √144=_____ g) √625
4
=_____ h) √1331
3
=_____ i) √512
3
=_____ j)√1000
3
=_____
13) Calcule:
21=2 22=2x2=____ 23=2x2x2=_____ 24=2x2x2x2=____
25=2x2x2x2x2=____ 26=2x2x2x2x2x2=____ 27=2x2x2x2x2x2x2=____
28=2x2x2x2x2x2x2=____ 29=2x2x2x2x2x2x2x2x2=____ 210=2x2x2x2x2x2x2x2x2x2=____
14) Diga quanto é:
210=______ 29=______ 28=______ 27=______ 26=______
25=______ 24=______ 23=______ 22=______ 21=______ 20=______
15) Se A= 49 , B=5+3, C= 144 , calcule:
a) A+B b) B+C c) 2.A d) B. C e) C.A+2.B
16) Se A= 549  e B= 3144  , ache A+B

3. 17) Se A= 36.25  B= 169196  e C=A+B
Ache: a) A+B+C b) 2.A.C
18) Se A= 25 , B=7+2, C= 9.2 , ache:
a) A+B+C
b) 2.A+C
19) Sei que A= 236.3  , B= A 925 , C= 5A , ache a metade de A+B+C.
20) Ache A+B, se
A= )361(5  e
B= 49.25  .
Sendo
A= )49.23)(365( 
B= 2).425(5 
C= 49.25  , ache A+B+C
21) Qual é a área do quadrado:
Exemplo: Faça o mesmo com:
Lado = 5 cm
A= ___cm x___ cm =____ cm2
22) Qual é o lado do quadrado, dada a área:
Exemplo:
Área = 121 m2
Lado = √___𝑚2=___m
23) Se 52361x52361=2741674321, calcule 2741674321.

4. 24) A e B são números naturais. Se AxA=B, quanto vale B ?
25) Ache a terça parte de 324
26) Se AxA=B e BxB=C, ache:
a) C b) B c) C
27) Se 14196  e 15225  . Responda: existe 200 exata?
28) Se 332x332=110224 e 333x333=110889. Pode existir raiz quadrada exata de 110750?
29) Calcule:
a) 169  c) 4.9 b) 169  d) 4.9
30) Calcule:
a) 25144  b) 25144  c) 25.144 d) 25.144
31) Se A= 36 e B= 144 , ache o valor de A+B.
32) Qual o volume do cubo:
Exemplo: Faça o mesmo:
33) Dado o volume do cubo, ache a medida da aresta

5. 34) a) Qual fração representa “meio bolo”? ________
b) Qual fração representa “um quarto de bolo”? ________
c) O que é mais? ½ bolo ou ¼ bolo? _______
d) Que fração é maior ½ ou ¼ ? ________
e) Quantos quartos são ½ bolo + ¼ de bolo? ____
f) Podemos dizer então que
1
2
+
1
4
=
35) Veja a torta de morango ao lado?
a) Qual fração da torta foi comida? _____
b) O que é maior ½ de uma torta ou 1/3 de uma torta? _____
c) O que é maior ½ de uma torta ou 2/3 de uma torta?
36) Veja os desenhos ao lado e responda:
Quanto é
1
2
+
1
4
=
(Observe os desenhos e entenda!)
37) Veja o desenho e responda:
a) O que é maior? ¼ ou 1/5? __________
(Respondeu olhando no desenho? É para olhar no
desenho!)
b) O que é maior 1/10 ou 1/8? _________
c) O que é maior 1/5 ou 1/3? _________
d) O que é maior 1/8 ou 1/15? ____________
Que regra você descobriu?
38) Veja as frações equivalentes. Mostre com desenhos que 1/4=2/8.

6. 39) Yasmin & Davi Ltda montaram um negócio de VENDA DE TRUFAS.
Yasmin fornece de cada 5 trufas, 2 para Davi. Ou seja, Davi fica com 2/5 das Trufas.
Se Yasmin fornecer 4 trufas de cada 10, Davi ganhará mais menos ou mesma coisa?
E se Yasmin fornecer 6 trufas de cada 15?
Represente as FRAÇÕES EQUIVALENTES.
40) Veja o desenho e responda o que se pede:
a) Qual é a menor fração
representada?
b) Qual é a maior fração
representada?
c) Qual das frações é maior que 1
inteiro?
d) Como podemos representar 5/4
como número misto?
41) Veja o exemplo e faça o mesmo com os outros desenhos
42) Desenhe as frações impróprias e transforme-as em número misto
Exemplo:
11
9

7. Faça você:
8
3
5
2
7
5
11
3
43) Agora é o contrário. Desenhe os números mistos e represente como fração imprópria:
1
2
3
2
1
2
44) Veja e faça o mesmo com os demais números
46. Veja com o desenho uma “regra”:
Sem fazer o desenho, agora você conseguirá transformar os
números mistos em frações impróprias sem desenhar:
a) 2
1
5
b) 3
3
4
c) 10
2
3
d) 15
1
2