Este documento contém um teste final de Matemática do 2o ciclo com questões sobre geometria plana e espacial, áreas e perímetros, proporcionalidade, estatística, volumes, números inteiros e decimais e fracções. O teste é composto por sete partes e inclui exercícios como classificação de figuras geométricas, cálculo de áreas e perímetros, resolução de problemas de proporcionalidade e percentagens.

1. Teste final – 2º ciclo – Matemática
Nome: ______________________ Nº _____ Turma: ______
ÍNDICE
PRIMAVERA..........................................................................................................................13
PRIMAVERA..........................................................................................................................28
I- Polígonos, Triângulos, Quadriláteros, simetrias, ângulos,
sólidos geométricos
1. Considera as seguintes figuras planas:
1

2. Indica as que são:
1.1. polígonos
1.2. pentágonos
1.3. quadriláteros
1.4. triângulos
2. Observa e completa:
2.1. Completa:
_________ são poliedros;
_________ são prismas;
_________ são pirâmides;
_________ não são poliedros.
2.2. Indica o número de faces, vértices e arestas dos sólidos B, C e I.
2.3. Indica o nome dos sólidos A, B e H.
2.4. Qual o nome do sólido que tem 14 vértices e 9 faces? (não
necessariamente presente na figura).
2.5. Qual o nome do sólido que tem 9 vértices e 16 arestas? (não
necessariamente presente na figura).
2

3. 3. Qual é o sólido geométrico que corresponde a cada uma das planificações
seguintes?
4. Observa os triângulos A, B, C, D e E e completa a tabela:
3

4. 5. Classifica, quanto aos lados e quanto aos ângulos, os seguintes triângulos:
2,50 cm 2,50 cm
A
C
B
2,50 cm
F
D E
2,25 cm
2,25 cm
G
I
H
50º 20º
5.1. Determina a amplitude do ângulo desconhecido do triângulo [GHI].
6. É possível construir um triângulo cujos lados tenham as medidas 2 cm, 4
cm e 6 cm?
7. Um ângulo agudo de um triângulo rectângulo tem de amplitude 35º.
Calcula a amplitude do outro ângulo agudo.
8. Dois ângulos de um triângulo têm de amplitude 40º e 35º respectivamente.
8.1. Calcula a amplitude do outro ângulo.
8.2. Classifica o triângulo quanto aos ângulos.
9. Dois ângulos de um triângulo têm de amplitude 40º e 75º respectivamente.
Calcula a amplitude do outro ângulo.
10. Indica a amplitude do ângulo desconhecido e classifica-o:
10.1.
4

5. 10.2.
11. Observa a figura e completa o quadro:
12. Dos quadriláteros abaixo representados, indica os que são:
12.1. Paralelogramos 12.2. Rectângulos
12.3. Losangos 12.4. Trapézios
12.5. Quadrados
5

6. 13. Considera os seguintes quadriláteros:
13.2 Traça os eixos de simetria dos quadriláteros representados.
13.3 Considerando como unidade cada quadrícula, calcula a área do
quadrilátero I e do E.
13.4. Indica as características das diagonais dos quadriláteros I, E, D e G.
13.5. Considerando como unidade cada 2 quadrículas, calcula a área do
quadrilátero I e do E.
14. Traça o eixo de simetria de cada uma das figuras seguintes:
6
13.1 Classifica os quadriláteros.

7. II – Áreas e Perímetros
1. O terreno representado na figura foi comprado a 5 euros o metro quadrado.
Quanto custou o terreno?
2. Considera as seguintes figuras:
7

8. 2.1. Determina a área das figuras A e B, tomando para unidade, primeiro
a área da figura 1 e depois a área da figura 2.
2.2. As figuras A e B são equivalentes? Justifica.
2.3. Tomando para unidade o lado de uma quadrícula como sendo 1 cm,
determina o perímetro da figura A.
3. Completa o quadro (π = 3,14)
4. Num jogo da selecção nacional de futebol, o jogador Luís Figo não jogou de
início. A determinada altura o seleccionador mandou-o fazer exercícios de
aquecimento, dando duas voltas à pista de atletismo em redor do campo.
Além disso, disse ao jogador Nuno Gomes para correr 2100 m na pista.
4.1 Quantos metros correu o Luís Figo?
4.2 Quantas voltas à pista foram dadas pelo Nuno Gomes?
8

9. 5. A figura representa um terreno de forma poligonal.
5.1. Quantos metros de rede serão necessários para vedar o terreno?
5.2. Sabendo que o pedreiro fez 5 metros por dia, calcula o número de
dias que foram precisos para fazer o muro.
6. Calcula a área da figura:
5 cm 8 cm
9
6 cm

10. III- Proporcionalidade, escalas e percentagens
1. A dona Amélia é florista e na sua loja, a relação existente entre o número de
tulipas e o número de ramos é traduzida pela seguinte tabela:
1.1. Verifica que há proporcionalidade directa entre o número de túlipas e o
número de ramos.
1.2. Qual é a constante de proporcionalidade? O que significa neste caso?
2. A Rita e o Diogo dividiram entre si os berlindes que receberam do irmão mais
velho na razão de 2 para 3. A Rita recebeu 18 berlindes.
Quantos berlindes recebeu o Diogo?
3. A Mariana teve um desconto de 20% na compra de um computador que
estava marcado por 1250 euros.
Quanto pagou a Mariana pelo computador?
4. Um “Boeing 707” (avião) tem de comprimento 57,5 m aproximadamente.
A que escala o deves desenhar para que o seu comprimento no desenho seja
5,75 cm?
10

11. 11

12. IV - Estatística
1. Numa turma do 7º ano, a avaliação do 1º período na disciplina de
Matemática foi:
3 4 4 4 3 2 3 4 2 3 4 4 4 4 2 3 3 4 5 4 3 3 2
3 2 5
1.1 Constrói uma tabela de frequências absolutas.
1.2 Calcula a média e a moda.
2. O tempo obtido numa prova de atletismo está registado no gráfico seguinte:
12
2.
2.
2.
2.

13. 3. Observa o seguinte pictograma:
3.1. Indica o número de crianças que gostam do Inverno.
3.2. Qual a estação favorita das crianças?
3.3. Determina o número total de crianças inquiridas.
4. Completa a seguinte tabela de frequências absolutas:
Estação do Ano Preferida Frequência Absoluta
Primavera
Verão
Outono
Inverno
Total
V - Volumes
1. Qual o volume do cilindro?
8 cm
5 cm
13

14. 2. Qual é o volume do sólido seguinte, se = 1 cm3 ?
3. Um aquário, com a forma de um paralelepípedo rectângulo, tem as
dimensões indicadas na figura:
Quantos litros de água são necessários para encher o aquário?
VI – Números inteiros e decimais
1. Considera os números: 0, 1, 2, 3, 5, 8, 25, 23, 12, 20, 300, 80, 31
Indica os que são:
1.1. múltiplos de 2
1.2. múltiplos de 3
1.3. divisíveis por 5
1.4. múltiplos de 3 e de 5
1.5. divisíveis por 10
1.6. divisores de 24
1.7. divisores de 300
1.8. múltiplos de 100
14

15. 2. Calcula mentalmente:
2.1. 6,29 x 1000 =
2.2. 75,1 : 0,01 =
2.3. 65,04 : 10 =
2.4. 76,3 x 0,01 =
2.5. 55,21 : 1000 =
3. Considera o seguinte número: 8 0 3 2 5 , 6 4 9
3.1. Escreve uma leitura do número.
3.2. Indica as ordens do algarismo 3 e do algarismo 4.
3.3. Quantas décimas tem o número.
4. Representa na recta numérica os números 5,2 6,4 6,7
5. Dados os conjuntos:
A = {0, 3, 6, 9} B = {números pares menores que 3,4}
5.1. Representa o conjunto A em compreensão.
5.2. Representa o conjunto B em extensão.
5.3. Indica um elemento que pertença aos dois conjuntos.
6. Dados os conjuntos:
C= {0, 3, 6, 9, 12, 15, 18} D = {números pares menores que 5,4}
15

16. 6.1. Representa o conjunto C em compreensão.
6.2. Representa o conjunto D em extensão.
7. Coloca os números seguintes por ordem decrescente:
456,23 546,2 2015,01 546,25 456,2 2013,01 465
8. Indica se é verdadeira ou falsa cada uma das afirmações seguintes:
8.1. 7 Î {1,3, 5, 7, 9 };
8.2. 0 Ï{números naturais};
8.3. 13 Î {números pares}.
8.4. 6,5 Î IN.
8.5. 4 Î D16
8.6. 34 Î M4
9. Calcula o valor numérico das expressões seguintes:
9.1. 10´ 6 ¸ 3 +10 ¸ 5 + 32 ;
9.2. 65 - 240 ¸( 2 + 2´4) +52 ;
9.3. 5300 : 10
9.4. 16,35 : 10
9.5. 1,87 ´ 10
9.6. 230 - (36-15) +21
9.7. 0,4 - (0,1 + 0,2) - (0,15-0,05)
16

17. 9.8. 12 – 2 ´ 10 : 5
9.9.
9.10. 40 -(1+5´4) -5
9.11. 10´6 ¸3 +10 ¸5 + 3
9.12. 3´(23 + 32 ) + 5
9.13. 65 - 240 ¸( 2 + 2´4) + 32
10. O automóvel do pai do Francisco custou 10 000 euros. Para o pagamento do
automóvel ele deu 2500 euros e o restante foi distribuído por 12 prestações
iguais. Qual o valor de cada prestação?
10.1. Escreve a expressão numérica que representa o valor de cada prestação.
10.2. Calcula o valor de cada prestação.
11. O Tiago foi ao supermercado e trouxe 2 Kg de cenouras mais dois pães que
pesavam cada um 0,5 Kg.
17

18. 11.1. Escreve a expressão numérica que representa o peso total em compras
que o Tiago trazia para casa?
11.2. Calcula o valor desse peso.
12. Traduz para linguagem matemática:
12.1 A soma de metade de dezoito com o quádruplo de cinco;
12.2 O quociente da soma de oito com catorze pela diferença entre dezasseis e
dez.
18

19. VII - Fracções
1. Cada uma das figuras está dividida em partes iguais.
Escreve, para cada caso, uma fracção correspondente à parte colorida.
1.1. Faz a leitura das fracções da alínea anterior.
2. Completa:
5 = 10
... 2.3 =
3
...
10 =
3. Transforma em fracções irredutíveis:
64
3.1. =
80
105
3.2. =
225
18
4. Calcula e apresenta o resultado sob a forma de fracção irredutível:
5 ´ - 1
4.1 ¸
3;
2
7
4
3
4.2
2 1 1 3 1;
3 2 7
æ ö + ¸ - çè ÷ø
19
2.1
...
6
6
2.2
14 2
...
= 2.4
3
15
3.3.
30
=

20. 4.3 23 0,5 7 3 .
´ æ + ö ¸ çè ÷ø
2 10
5. Calcula e apresenta o resultado sob a forma de fracção irredutível:
17
3 ÷ø
- æ 1 ÷ø
+
3
+ 5 + æ 3 - 1
- 5.1. 2
4
2
4
ö çè
ö çè
1
5 ÷ø
- æ 1 ÷ø
+
1
+ 7 - æ 0,3 - 1
- 5.2. 3
2
10
3
ö çè
ö çè
5.3.
æ-
4
öçè
÷ø
æ-+÷ø
çè
1
3
5
3
6
20
5.4.
5.5.
5.6.
5.7.
5.8.
5.9.
5.10
5.11
5.12
5.13

21. 6. Do seguinte conjunto de números indica:
9 ; 0,4; 1 ; 25 ; 6 ; 2 ; 26 ; 7
10 3 5 3 100 2 5
6.1. Quais são números fraccionários?
6.2. Quais são maiores do que um?
6.3. Quais são fracções decimais?
6.4. Ordena-os por ordem crescente.
7. Das fracções seguintes, indica:
; 1
8
100
; 6
; 4
2
10
; 5
3
; 9
7
; 3
6
; 3
4
10
; 6
3
7.1. As que representam números maiores que 1;
7.2. As que representam o número 1;
7.3. Duas fracções equivalentes;
7.4. As fracções decimais.
21

22. 8. Completa:
9. Completa com um dos sinais < , = , > :
......7
5
...... 2
9
...... 3
3
......6
7
...... 5
6
10. O Francisco tinha 12 livros de aventuras e 18 livros de banda desenhada.
Certo dia, resolveu dar
2
3
desses livros à Biblioteca da Escola.
10.1 Quais das expressões seguintes representam o número de livros que o
Francisco ofereceu à Biblioteca? (faz um círculo à volta da alínea correcta)
2 ´ + ; (b) (12 18)
(a) 12 18
3
2 ´ + ; (c) 18 12
3
2 ´ + ; (d) 18
3
2 ´ 12 + 2
´ .
3
3
10.2 Calcula esse número.
11. A Joana quer guardar 6 kg de amêndoas em embalagens de
4
3
kg. De
quantas embalagens vai precisar?
12. Escreve em linguagem simbólica:
22
9.1
5
3
9.2
9
4
9.3
100
10
9.4
8
6
9.5
4
5
9.6
1
......0,25
4

23. 12.8. O produto da soma de dois quintos com três, pelo quadrado de quatro.
12.9. O quociente entre a soma de oito com quinze, pela soma de dezasseis
com três quintos.
12.10. O quociente da soma de quinze com vinte e três pela diferença entre
dezasseis e nove.
12.11. A diferença entre o produto de dezoito por três e o quociente de vinte
por quatro.
12.12. O produto de quinze pela soma de três com seis é cento e trinta e
cinco.
13. A Patrícia, a Marta e a Ana dividiram entre si o bolo que fizeram. As duas
primeiras receberam respectivamente
1
6
e
1
.
3
Que fracção do bolo coube à Ana?
23
12.1
12.2
12.3.
12.4
12.5.
12.6.
12.7.

24. 14. A Susana anda a fazer um tapete de Arraiolos. Já bordou do
tapete mas enganou-se e vai ter que desmanchar do que fez. Que
fracção do tapete tem a Susana ainda de fazer?
15. O Diogo comeu do chocolate que a avó lhe deu e dividiu o restante, em
partes iguais, pelos seus 2 irmãos. Que fracção do chocolate deu a cada um
deles?
1
16. A Lili foi ao mercado comprar fruta. Comprou 20 peras. O Pepe comeu 4
2
.
das peras que a Lili comprou e o Alex comeu 5
16.1 Qual dos dois comeu mais peras?
2
1 +
16.2 O que representa a expressão: 4
5
?
16.3 Calcula a parte das peras que sobraram.
24

25. 16.4 Calcula quantas peras sobraram.
17. A Ana foi às compras tendo efectuado as compras seguintes:
4
Kg de bananas; 2,5 Kg de peras; 4
5
10
1
Kg castanhas
Kg de maçãs; 2
17.1 Diz o que representam as seguintes expressões:
a)
2,5
4 +
5
1
10 +
b) 4
2
17.2 Pesavam mais as peras ou as maçãs?
17.3 Pesavam mais as peras ou as bananas? Quanto mais?
17.4 Calcula o peso total das compras da Ana.
25

26. Correcção
I
1.1.- a, c, d, e, f, g, h, j, k.
1.2.- d, k.
1.3.- c, e, g, h.
1.4.- a, f, j.
2.1.- B, C, D, F, G, H, I.
B, D, G, I.
C, H.
A, E, J.
2.2.- B- f:8 v:12 a:18
C- f:4 v:4 a:6
I- f:6 v:8 a:12
2.3.- A- esfera
B- Prisma hexagonal
H- Pirâmide quadrangular
2.4.- Prisma hexagonal
2.5.- Pirâmide octogonal
3- A- Pirâmide quadrangular
B- Cilindro
C- Cone
D- Paralelepípedo rectângulo
4- A- isósceles, rectângulo
B- escaleno, obtusângulo
C- isósceles, acutângulo
D- escaleno, acutângulo
E- equilátero, acutângulo
5- [ABC]- equilátero e acutângulo
[DEF]- isósceles e rectângulo
[GHI]- escaleno e obtusângulo
5.1.- 180 – 50 – 20= 110º
6- Não. Pois a soma dos dois lados com um comprimento inferior deve ser
sempre menor que o comprimento do outro lado.
7- 180 – 35 – 90 = 55º
8.1.- 180 – 40 – 35 = 105º
8.2.- Obtusângulo.
9- 180 – 75 – 40= 165º
10.1.- 130º - obtusângulo
10.2.- 72º - agudo
11-
S HEF- Agudo
S AHG- Obtuso
S ABC- Raso
12.1.- 1,2,4,6,9,10,11,12,13,14,15
12.2.- 1,2,6,9,10,13
12.3.- 1,4,10,12,14
12.4.- 3,5
12.5.- 1,6,10
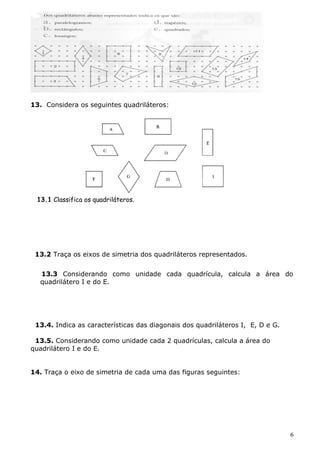
13.1.- A- trapézio
B- paralelogramo, rectângulo
C- paralelogramo
D- Paralelogramo
26

27. E- paralelogramo, rectângulo
F- losango, quadrado
G- losango
H- trapézio
I- Rectângulo, quadrado
13.3.- I- 16 E- 10
13.4.- I- diagonais concorrentes e perpendiculares, com igual comprimento
E- diagonais concorrentes e oblíquas, com igual comprimento
D- diagonais concorrentes e oblíquas, com diferente comprimento
G- diagonais concorrentes e perpendiculares, com igual
comprimento
13.5.- I- 8 E- 5
14-
II
1- A= 70 x 10 + 50 x 10 + 30 x 10 = 700 + 500 + 300 = 1500 m2
1500 x 5 = 7500 €
2.1.- A- 40 (fig 1), 20 (fig 2)
B- 32 (fig 1), 16 (fig 2)
2.2.- Não. Não têm a mesma área.
2.3.- PA= 2 x 4 + 2 x 6 = 8 x 12 = 20 cm2
3- A- 7; 21,98
B- 5; 31,4
C- 1,25; 2,5
4.1.- (98 x 3,14) + 110 x 2 = 307,72 + 220 = 527,72 m
4.2.- 527,72 : 2 = 263,86 – uma volta
2100: 263,86 = 7,95 quase oito voltas
5.1.- P= 17,5 + 18 + 15,5 + 11,5 + 20 + 12,5 = 95 m
5.2.- 95 : 5 = 19 dias
6.-
Acírculo= 3,14 x 32 = 3,14 x 9 = 27,26cm2 Asemi-círculo= 13,63 cm2
Arectângulo= 8 x 6 = 48 cm2
5 x 6 30 Atriângulo= = = 15 cm
2
2 2
Atotal= 13,63 + 48 + 15 = 76,63 cm2
27

28. III
1.1.-
2 =
4
16 32
1.2.-
2 : 2 =
1
16 8
2- 2 : 3
2 18
3
x
= ´ = =
18 3 54 27
2 2
=
x berlindes
3-
x
1250
100 80
1250 80 100000 1000€
100 100
x
=
= ´ = =
4- c= 57,5 m
5,75 5750
1
x
5750 : 5,75 1000
x
=
= =
1 : 1000
IV
1.1.-
Avaliação na disciplina de Matemática
Nota Contagem Frequência absoluta
2 |||| 5
3 |||| |||| 9
4 |||| |||| 10
5 || 2
1.2.- Moda é 4
Média = ´ + ´ + ´ + ´ = + + + = =
2 5 3 9 4 10 5 2 10 27 40 10 87 3,35
26 26 26
2.1.- Alex.
2.2.- Tuxa.
2.3.- Pepe e Ruca.
2.4.- 8 minutos.
3.1.- 40 crianças.
3.2.- Verão.
3.3.- 20 x 14 = 280 crianças
4-
Estação do Ano Preferida Frequência Absoluta
Primavera 80
Verão 100
Outono 60
Inverno 40
Total 280
28

29. V
1- Vcilindro= Ab x h = 3,14 x 52 x 8 = 3,14 x 25 x 8 = 3,14 x 200 = 628 cm3
2- Vsólido= 14 cm3
3- Vparalelepípedo rectângulo= 50 x 20 x 30 = 3000 cm3 = 3000 ml = 3 l
VI
1.1.- M2= {0,2,8,12,20,80,300}
1.2.- M3= {0,3,12,300}
1.3.- D5={5,20,25,80,300}
1.4.- M3 e M5= {0,300}
1.5.- D10= {20,80,300}
2.1.- 6290
2.2.- 75100
2.3.- 650,4
2.4.- 0,763
2.5.- 5,521
3.1.- Oitenta mil, trezentos e vinte e cinco unidades e quatrocentos e quarenta
e três milésimas.
3.2.- 3- centenas de unidades 4- centésimas
3.3.- 803,256 décimas
5.1.- A = {Múltiplos de três menores que dez}
5.2.- B= {0,2}
5.3.- zero
6.1.- C= {Múltiplos de três menores que dezanove}
6.2.- D= {0,2,4}
7- 2015,01>2013,01>546,25>546,2>465>456,23>456,2
8.1.- V 8.2.- F 8.3.- F 8.4.- F 8.5.- V 8.6.- F
9.1.- 60:3+10:5+32=20+10:5+9=20+2+9=31
9.2.- 65-240:10+25=65-24+25=41+25=66
9.3.- 530
9.4.- 1,635
9.5.- 18,7
9.6.- 230-21+21=230
9.7.- 0,4-0,3-0,1=0
9.8.- 12-29:5=12-4=8
9.9.- 100+10x4+6x10-10=100+40+60-10=190
9.10.- 40-21-5=14
9.11.- 60:3+2+3=20+2+3=25
9.12.- 3x(8+9)+5=3x17+5=46
9.13.- 65-240:10+9=65-24+9=41+9=50
10.1.- (10000-2500):12
10.2.- 7500:12=625€ mensais
11.1.- 2+2x0,5
11.2.- 2+1=3 kg
12.1.- 18:2+4x5=
12.2.- (8x14)-(16-10)
VII
1- 2/4=1/2; 5/9; 8/12=2/3; 4/6=2/3; 2/5
29

30. 1.1.- Dois quartos, cinco nonos, dois terços, três oitavos, dois terços e dois
quintos.
2.1.- 12
2.2.- 7
2.3.- 18
2.4.- 2
3.1.-
16 =
4
20 5
3.2.- 21/45
3.3.-
9 =
3
15 5
4.1.-
35 - 1 ´ 1 = 35 - 1 = 35 - 2 = 33 =
11
12 2 3 12 6 12 12 12 4
4.2.-
1 + 1 ´ 7 - 1 = 1 + 7 - 1 = 2 + 21 - 18 =
5
9 2 3 9 6 1 18 18 18 18
4.3.-
8 5 7 : 3 8 5 35 : 3 8 40 : 3 320 10 320
´æ + ö = ´æ + ö = ´ = ´ = çè ø¸ èç ø¸
10 2 10 10 10 10 10 10 10 3 3
5.1.-
3 2 3 5 6 1 17 3 5 5 5 17 12 5 20 10 17 7 20 10 17 27 10 17 37 17 20 5
-æ ö æ ö çè + + + - - = - + + - = - + + - = + + - = + - = - = = 4 4 ø¸ èç 2 2 ø¸
4 4 2 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
5.2.-
5 2 3 7 3 1 1 5 5 7 2 1 150 25 210 6 10 125 210 6 10 335 6 10 319
-æ + ö + - æ - ö - = - + - - = - + - - = + - - = - - = çè ø¸ èç ø¸
5.3.-
6 6 10 10 3 6 10 3 30 30 30 30 30 30 30 30 30 30 30 30 30
10 9 4 3 1 1 2 1
12 12 12 12 12 12 12 6
æ - ö + æ - ö = + = = çè ø¸ èç ø¸
5.4.-
7 + 3 = 10 =
5
8 8 8 4
5.5.-
25 ´ 1 - 1 = 25 - 1 = 25 - 5 = 20 =
2
10 2 10 2 10 10 10
5.6.-
4 + 1 - 1 = 12 + 1 - 9 = 13 - 9 =
4
3 9 9 2 9 9 9 9
5.7.-
1 + 1 =
9
8 8
5.8.-
1 : 2 = 1 ´ 5 =
5
3 5 3 2 6
5.9.-
1 + 4 ´ 10 = 1 + 2 =
3
5 4
5.10.-
30

31. 2 ´ 5 + 4 = 2 + 4 = 4 + 4 = 8 =
4
5 3 6 3 6 6 6 6 3
5.11.-
35 - 1 = 35 - 2 =
33
10 5 10 10 10
5.12.-
5 2 : 3 7 2 7
4 4 2 4 3 6
æ + ö = ´ = çè ø¸
5.13.-
1 + 1 ´ 9 - 1 = 1 + 9 - 1 = 9 - 8 =
1
8 4 2 8 8 8 8 8
6.1.- 9/10; 0,4; 1/3; 2/100; 7/5
6.2.- 25/5; 6/3; 26/2
6.3.- 9/10; 0,4; 2/100
6.4.-
2 < 1 < 0,4 < 9 < 1,4 < 6 < 25 <
26
100 3 10 3 5 2
7.1.- 10/3; 9/2
7.2.- 6/6, 3/3
7.3.- 6/6=3/3 ou ¾=6/8
7.4.- 4/10 e 1/100
8- 10/5; 2; 1; 5; 1/5
9.1.- < 9.2.- > 9.3.- > 9.4.- > 9.5.- < 9.6.- =
10.1.- b) e d)
10.2.- 2/3 x 30= 20
11.-
6 : 4/3 = 6 x ¾ = 9/2 = 4,5 5 embalagens.
12.1.- 3/5 + 2/7 12.2.- 9/7 – 0,3 12.3.- 2 x ( 11/4 + 2/3 )
12.4.- 3/8 x 8/3 12.5.- ¾ : 5 12.6.- 2 x ( 8 : 1/3 )
12.7.- 0,5 + ( 8 : 4 ) 12.8.- (2/5 + 3 ) x 42 12.9.- ( 8 + 15 ) : ( 16 + 3/5 )
12.10.- (15 + 23 ) : ( 16 – 9 ) 12.11.- (18 x 3) – (20 : 4)
12.12.- 15 x 3 + 7 = 135
13-
1 - 1 - 1 = 6 - 1 - 2 = 3 =
1
6 3 6 6 6 6 2
14-
1 - 4 + 1 = 40 - 32 + 5 = 8 + 5 =
13
5 8 40 40 8 40 40 40
15-
1 2 : 2 5 2 : 2 3 : 2 3 1 3 0,3
æ ö æ ö çè - ø¸ = èç - ø¸
= = ´ = = 5 5 5 5 5 2 10
16.1.- Alex.
1 =
5
4 20
2 =
8
5 20
16.2.- A fracção da fruta que o Pepe e o Alex comeram.
16.3.-
5 8 13
20 20 20
æ + ö = çè ø¸
31

32. 16.4.-
1 1 2 20 5 8 20 13 7
- æ + ö = - æ + ö = - = çè ø¸ èç ø¸
4 5 20 20 20 20 20 20
17.1.- a) Peso das bananas e da pêras.
b) Peso das maças e das castanhas.
17.2.- 25/10 = 2,5 e 10/4 = 2,5 pesam a mesma coisa.
17.3.- 4/5 = 0,800 kg 2,500 – 0,800 = 1,700 kg
17.4.-
4 2,5 10 1 4 25 10 1 16 50 50 10 126 6,300
5 4 2 5 10 4 2 20 20 20 20 20
+ + + = + + + = + + + = = kg
32