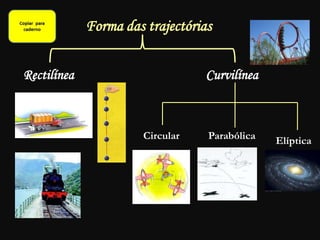
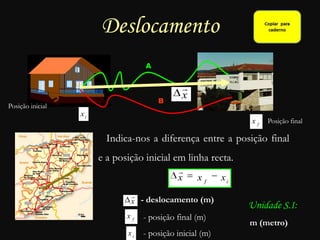
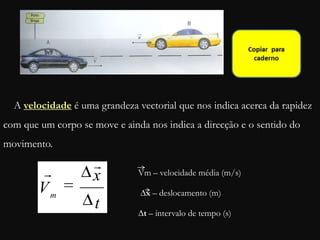
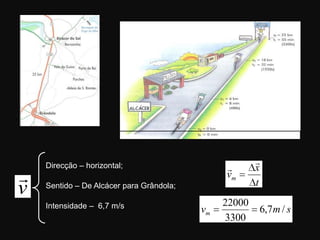
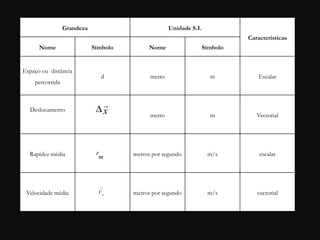
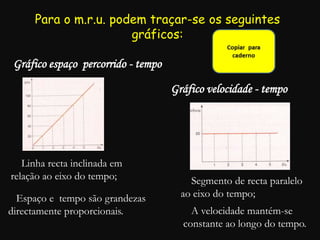
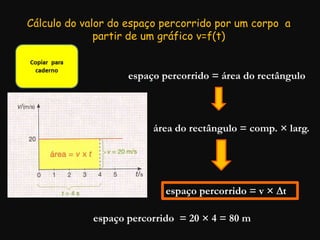
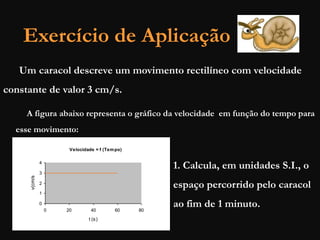
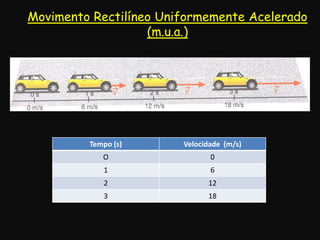
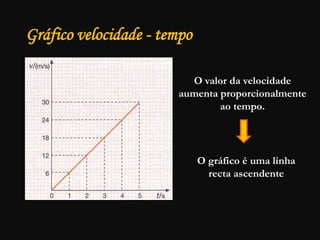
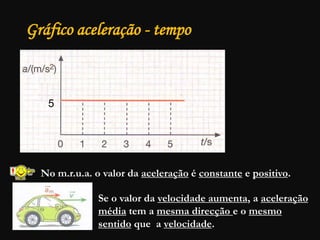
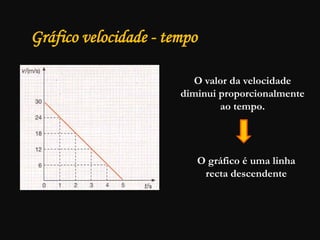
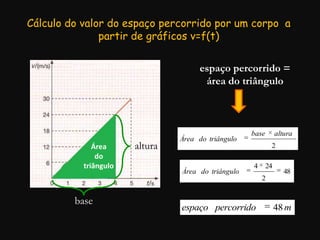
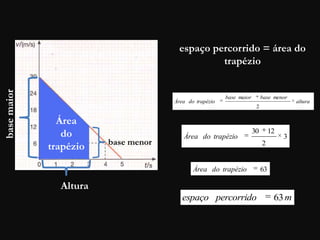
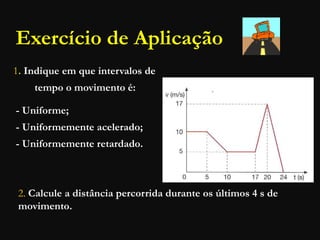
O documento descreve conceitos fundamentais de movimento, incluindo repouso, referencial, trajetória, deslocamento, velocidade média e tipos de movimento. Aborda movimento retilíneo uniforme, uniformemente variado, uniformemente acelerado e retardado.

1. Estudo de movimentos

2. Descrição do movimento

3. Repouso e Movimento de um corpo
Repouso - diz-se que um corpo está em repouso quando
a sua posição não varia ao longo do tempo.
Movimento – diz-se que um corpo está em movimento
quando a sua posição varia ao longo do tempo.
Repouso e movimento são conceitos relativos
É necessário indicar sempre o referencial em relação ao
qual o movimento se efectua.

4. Referencial
Para descrever o movimento de um corpo é necessário
escolher, previamente, um referencial.
Referencial – ponto de referência relativamente ao qual se analisa
a variação da posição do corpo em estudo, ao longo do tempo.
Um corpo pode estar em movimento relativamente a um
dado referencial e em repouso em relação a outro..

5. A B
Será que a águia B está efectivamente em repouso?
A águia da figura B encontra-se:
Em repouso, quando tomamos como referência a árvore;
Em movimento, relativamente ao Sol.

6. Exercício de Aplicação 1
Para um observador A, a carrinha está em ____________.
Para um observador B, a carrinha está em ____________.
movimento
repouso

7. Trajectória
Trajectória - linha imaginária que define as sucessivas posições
ocupadas por um corpo durante o seu movimento..
A
B

8. Forma das trajectórias
Rectilínea Curvilínea
Circular Parabólica Elíptica

9. Espaço percorrido
Comprimento da trajectória Espaço Percorrido/ Distância percorrida
Unidade S.I: m (metro)
É uma grandeza que nos dá o comprimento do percurso efectuado
desde o ponto de partida até ao ponto de chegada.

10. x

Corresponde a um vector que tem:
x

Direcção - é a linha recta que une a posição inicial à posição final.
Sentido - da posição inicial para a posição final.
Ponto de aplicação – corresponde à posição inicial ocupada pelo
corpo.
Intensidade - valor igual à diferença entre a posição final e a posição
inicial, em linha recta.
Deslocamento

11. Deslocamento
A
B
Posição inicial
i
x
Posição finalf
x
Indica-nos a diferença entre a posição final
e a posição inicial em linha recta.
if
xxx

- deslocamento (m)
- posição final (m)
- posição inicial (m)
x

i
x
f
x
x

Unidade S.I:
m (metro)

12. Exercício de Aplicação 2
Uma tartaruga encontra-se a 0,7 m da origem das posições e ao fim
de 30 s localiza-se na posição 0,3m, percorrendo uma trajectória
rectilínea.
xi = 0,7 m
ti = 0 s
xf = 0,3 m
tf = 30 s
x (m)
Calcula:
1. O deslocamento da tartaruga.
2. A distância percorrida pela tartaruga, durante o seu movimento.
3. Representa, na figura, o vector deslocamento.
4. Caracteriza o vector deslocamento.

13. Rapidez média
Medalhados nos jogos olímpicos de atenas – 2004
Prova de Atletismo – 100 m
CLASSIFICAÇÃO ATLETA (NACIONALIDADE) TEMPO
1º J. Gatlin (USA) 9,85 s
2º F. Obikwelu (Port.) 9,86 s
3º M. Greene (USA) 9,87 s
Rapidez média =Rapidez média =
rm – rapidez média (m/s)
d – distância percorrida (m)
∆t – intervalo de tempo (s)
t
d
r
empoervalo
eercorridopespaço
médiaRapidez m
tdeint
Unidade S.I: m/s
(metros por segundo)

14. Velocidade média
A velocidade é uma grandeza vectorial caracterizada por:
Direcção
- a direcção da trajectória no caso do movimento rectilíneo;
- a direcção da tangente à trajectória se o movimento é curvilíneo.
Sentido – o do movimento;
Ponto aplicação – coincide com a posição ocupada pelo corpo no instante considerado;
Intensidade – corresponde ao valor da rapidez média.

15. t
x
Vm
 Vm – velocidade média (m/s)
∆x – deslocamento (m)
∆t – intervalo de tempo (s)
A velocidade é uma grandeza vectorial que nos indica acerca da rapidez
com que um corpo se move e ainda nos indica a direcção e o sentido do
movimento.

16. v

Direcção – horizontal;
Sentido – De Alcácer para Grândola;
Intensidade – 6,7 m/s
t
x
vm


smvm /7,6
3300
22000

17. Grandeza Unidade S.I.
Características
Nome Símbolo Nome Símbolo
Espaço ou distância
percorrida
d metro m Escalar
Deslocamento
metro m Vectorial
Rapidez média metros por segundo m/s escalar
Velocidade média metros por segundo m/s vectorial
x

m
V

m
r

20. Tipos
de
Movimento

21. O movimento de um corpo pode classificar-se
de acordo com:
a trajectória descrita por esse corpo;
a velocidade adquirida durante o seu movimento.
Linha recta Velocidade se mantém constante
tanto em valor numérico como em
direcção e sentido
Movimento Rectilíneo Uniforme (m.r.u.)

22. Tempo (s) Espaço percorrido (m)
0 0
1 20
2 40
3 60
4 80
5 100

23. Conclusão:
No movimento rectilíneo uniforme o corpo percorre espaços
iguais em intervalos de tempo iguais;
O espaço percorrido e o tempo gasto a percorrê-lo são
directamente proporcionais.
A velocidade do corpo mantém-se constante em valor, direcção
e sentido.
Movimento Rectilíneo Uniforme

24. Para o m.r.u. podem traçar-se os seguintes
gráficos:
Gráfico espaço percorrido - tempo
Gráfico velocidade - tempo
Linha recta inclinada em
relação ao eixo do tempo;
Espaço e tempo são grandezas
directamente proporcionais.
Segmento de recta paralelo
ao eixo do tempo;
A velocidade mantém-se
constante ao longo do tempo.

25. Cálculo do valor do espaço percorrido por um corpo a
partir de um gráfico v=f(t)
espaço percorrido = área do rectângulo
área do rectângulo = comp. × larg.
espaço percorrido = v × t
espaço percorrido = 20 × 4 = 80 m

26. Exercício de Aplicação
Um caracol descreve um movimento rectilíneo com velocidade
constante de valor 3 cm/s.
A figura abaixo representa o gráfico da velocidade em função do tempo para
esse movimento:
Velocidade = f (Tempo)
0
1
2
3
4
0 20 40 60 80
t (s)
v(cm/s)
1. Calcula, em unidades S.I., o
espaço percorrido pelo caracol
ao fim de 1 minuto.

27. O movimento de um corpo pode classificar-se de acordo
com:
a trajectória descrita por esse corpo;
a velocidade adquirida durante o seu movimento.
Linha recta Velocidade varia ao longo do tempo
Se os valores da velocidade
aumentam, dizemos que o
movimento é acelerado
Se os valores da velocidade
diminuem, dizemos que o
movimento é retardado
Movimento Rectilíneo Uniformemente Variado (m.r.u.v)

28. Movimento Rectilíneo Uniformemente Acelerado
(m.u.a.)
Tempo (s) Velocidade (m/s)
O 0
1 6
2 12
3 18

29. Gráfico velocidade - tempo
O valor da velocidade
aumenta proporcionalmente
ao tempo.
O gráfico é uma linha
recta ascendente

30. Gráfico aceleração - tempo
5
No m.r.u.a. o valor da aceleração é constante e positivo.
Se o valor da velocidade aumenta, a aceleração
média tem a mesma direcção e o mesmo
sentido que a velocidade.

31. Movimento Rectilíneo Uniformemente Retardado
(m.u.r.)
Tempo (s) Velocidade (m/s)
O 18
1 12
2 6
3 0

32. Gráfico velocidade - tempo
O valor da velocidade
diminui proporcionalmente
ao tempo.
O gráfico é uma linha
recta descendente

33. Gráfico aceleração - tempo
No m.r.u.r. o valor da aceleração é constante e negativo.
5
Se o valor da velocidade diminui, a
aceleração média tem a mesma direcção
mas sentido contrário ao da velocidade.

34. Cálculo do valor do espaço percorrido por um corpo a
partir de gráficos v=f(t)
Área
do
triângulo
altura
base
espaço percorrido =
área do triângulo
2
alturabase
triângulodoÁrea
48
2
244
triângulodoÁrea
mpercorridoespaço 48

35. Área
do
trapézio base menor
espaço percorrido = área do
trapézio
Altura
basemaior
altura
menorbasemaiorbase
trapéziodoÁrea
2
3
2
1230
trapéziodoÁrea
63trapéziodoÁrea
mpercorridoespaço 63

36. Exercício de Aplicação
1. Indique em que intervalos de
tempo o movimento é:
- Uniforme;
- Uniformemente acelerado;
- Uniformemente retardado.
2. Calcule a distância percorrida durante os últimos 4 s de
movimento.