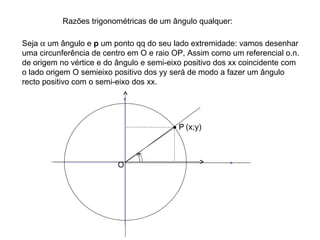
1. Razões trigonométricas de um ângulo qualquer: Seja  um ângulo e p um ponto qq do seu lado extremidade: vamos desenhar uma circunferência de centro em O e raio OP, Assim como um referencial o.n. de origem no vértice e do ângulo e semi-eixo positivo dos xx coincidente com o lado origem O semieixo positivo dos yy será de modo a fazer um ângulo recto positivo com o semi-eixo dos xx. (x;y) O  P

2. Para se poder falar de razões trigonométricas de um ângulo qualquer  elas vão ser assim definidas Por exemplo .Determine as razões trigonométricas de um ângulo com o vértice na origem do referencial, cujo lado origem está sobre o semieixo positivo dos xx e cujo lado extremidade contém o ponto de coordenadas: a) (4; 3) b) (-5;12) c) (-6;-8) xx` x  P(x;y) y O  yy

3. sin  = : cos  = ; tg  = A) xx` x  P(x;y) y O  yy

4. xx` -5  P(-5;12) 12 O yy  sin  = : cos  = tg  = B)

5. sin  = : cos  = ; tg  = C) xx` -6  P(x;y) -8 O  yy

6. Notas:  se o denominador for zero a razão trigonométrica não existe.  O valor da razão trigonométrica não depende do raio da circunferência, mas se o raio for igual a um facilita os cálculos. Nesta situação o círculo passa a chamar-se circulo trigonométrico. Círculo trigonométrico é um círculo de raio um e centro na origem do referencial Determine as razões trigonométricas de um ângulo com o vértice na origem do referencial, cujo lado origem está sobre o semieixo positivo dos xx e cujo lado extremidade contém o ponto de coordenadas : Nota: No círculo trigonométrico o seno de um ângulo é igual à ordenada do ponto do ângulo que está sobre o círculo e o co-seno é igual à abcissa do mesmo ponto . xx` x  P(x;y) y O  yy