O documento apresenta uma aula sobre juros simples com o objetivo de conceituar e calcular juros simples. A aula inclui atividades de aquecimento, principal, discussão de soluções e sistematização do conceito, com resolução de exemplos para fixar o conteúdo sobre juros simples.

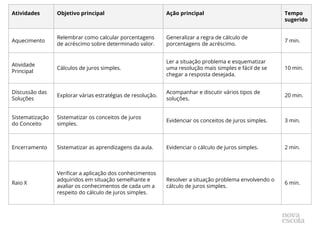
1. Atividades Objetivo principal Ação principal Tempo
sugerido
Aquecimento
Relembrar como calcular porcentagens
de acréscimo sobre determinado valor.
Generalizar a regra de cálculo de
porcentagens de acréscimo.
7 min.
Atividade
Principal
Cálculos de juros simples.
Ler a situação problema e esquematizar
uma resolução mais simples e fácil de se
chegar a resposta desejada.
10 min.
Discussão das
Soluções
Explorar várias estratégias de resolução.
Acompanhar e discutir vários tipos de
soluções.
20 min.
Sistematização
do Conceito
Sistematizar os conceitos de juros
simples.
Evidenciar os conceitos de juros simples. 3 min.
Encerramento Sistematizar as aprendizagens da aula. Evidenciar o cálculo de juros simples. 2 min.
Raio X
Verificar a aplicação dos conhecimentos
adquiridos em situação semelhante e
avaliar os conhecimentos de cada um a
respeito do cálculo de juros simples.
Resolver a situação problema envolvendo o
cálculo de juros simples.
6 min.

2. Objetivo: Conceituar e calcular juros simples

3. Joaquim foi no banco conferir seu saldo.
Em sua última consulta, tinha R$ 3400,00,
durante o mês ele fez um depósito de R$
500,00, pagou algumas contas no débito
que totalizaram R$ 980,00 e fez um
pagamento em cheque de R$ 320,00. Qual
será o saldo após essas transações
financeiras? Após 30 dias, sabe-se que o
dinheiro rende 2% de aumento. Ao passar
1 mês, quando Joaquim voltar ao banco e
consultar seu saldo, que valor deverá
encontrar?

4. Resolução:
Seu último saldo era de R$ 3400,00, fez um depósito de R$ 500,00 e
pagou algumas contas que totalizaram R$980,00, também fez um
pagamento com cheque de R$ 320,00.
Então, devemos somar o depósito e retirar os pagamentos:
3400 + 500 - 980 - 320 = 2600.
Após as transações financeiras, o seu novo saldo é de R$ 2600,00.
Agora vamos encontrar 2% de 2600:
Mentalmente: 1% de 2600 é 26 reais, então 2% de 2600 é 52 reais.
Seu saldo após o rendimento será R$2652,00.
Ou,
calculando diretamente: como queremos um aumento de 2%, basta
multiplicar por 1,02, então 1,02 . 2600 = 2652 reais.

5. Juliana foi ao banco solicitar um
empréstimo de R$ 15 000,00. Ela terá que
pagar essa quantia ao término de 3 anos,
com taxa de juros simples de 3% ao mês.
Quanto ela pagará de juros? Qual o
montante vai ser pago por Juliana ao
banco no final do empréstimo?

6. Mentalmente
O capital emprestado é de R$ 15 000,00.
O juro é de 3% ao mês.
1% é a centésima parte de 15000, ou seja, 15000 : 100 = 150.
Assim 3% = 3 . 150 = 450.
O prazo da dívida é de 3 anos = 36 meses (1 ano = 12 meses).
Podemos calcular assim: 10 anos + 10 anos + 10 anos + 6 anos = 4500 +
4500 + 4500 + 6x450= 16 200.
Portanto, Juliana deverá pagar R$ 16200,00 de juros ao banco.
Para saber a quantia final a ser paga, devemos acrescentar o capital com
o juros: 15000 + 16200 = 31 200 (isto é conhecido como montante).

7. Geometricamente
15 000
Capital inicial
Taxa de 3 %
450 450 450 450 450 450 450 450 450 450
450 450 450 450 450 450 450 450 450 450
450 450 450 450 450 450 450 450 450 450
450 450 450 450 450 450
tempo:
36 meses
Juros: 16200
Montante: 15000 + 16200 = 31 200

8. Outra resolução:
O capital emprestado é de R$ 15 000,00.
O prazo da dívida é de 3 anos = 36 meses.
O juro é de 3% ao mês.
Primeiro, vamos calcular o juro de 3% ao mês.
3% de 15 000 = 0,03 x 15 000 = 450.
Como o intervalo de tempo é 36 meses e nesse sistema o cálculo de juro é
sempre sobre o capital inicial, devemos multiplicar o juro de um mês por
36: 450 x 36 = 16 200.
Portanto, Juliana deverá pagar R$ 16 200,00 de juros ao banco.
Para saber a quantia final a ser paga, devemos acrescentar o capital com
o juros: 15000 + 16200 = 31 200.

9. Outra resolução:
O capital emprestado é de R$ 15 000,00.
O prazo da dívida é de 3 anos = 36 meses ( 1 ano = 12 meses).
O juro é de 3% ao mês.
Então, podemos multiplicar o tempo pela taxa de juros 36 x 3% = 108%,
transformando em número decimal, temos 1,08.
Em seguida, multiplicamos pelo capital: 1,08 x 15 000 = 16 200.
Portanto, Juliana deverá pagar R$ 16200,00 de juros ao banco.
Para saber a quantia final a ser paga devemos acrescentar o capital com o
juros: 15000 + 16200 = 31 200 (isto é conhecido como montante).

10. Outra resolução:
O capital emprestado é de R$ 15 000,00.
O prazo da dívida é de 3 anos = 36 meses (1 ano = 12 meses).
O juro é de 3% ao mês, transformando a porcentagem em decimal temos
0,03.
Então, podemos multiplicar o tempo pela taxa de juros 36 x 0,03 = 1,08.
Em seguida, multiplicamos pelo capital: 1,08 x 15 000 = 16 200.
Portanto, Juliana deverá pagar R$ 16200,00 de juros ao banco.
Para saber a quantia final a ser paga, devemos acrescentar o capital com
o juros: 15000 + 16200 = 31 200 (isto é conhecido como montante).

11. Utilizando fórmulas:
Note que, para determinar a quantia de juros, multiplicamos o valor do
empréstimo (capital), pela taxa de juros e pelo intervalo de tempo.
Generalizando essa ideia, temos esta fórmula:
juros = capital(c) x taxa(i) x tempo(t)
j = C . i . t
j = 15 000 . 0,03 . 36 = 16 200.
Portanto, Juliana deverá pagar R$ 16 200,00 de juros ao banco.
Para saber a quantia final a ser paga, devemos acrescentar o capital com
o juros, o montante:
M = C + j
M = 15000 + 16200 = 31 200.

12. Os juros simples são resultados da
multiplicação do capital inicial pela taxa e
por um determinado período de tempo.
Podemos utilizar a fórmula para calcular o
juros simples: j = C . i . t
A taxa de juro e o intervalo de tempo
devem estar sempre na mesma unidade,
por exemplo, se a taxa de juro é dada em
mês, o tempo também devem estar em
meses.
Sobre o tempo, utilizamos o mês comercial
de 30 dias e o ano comercial de 360 dias.

13. Capital (C) é o dinheiro que se empresta ou que se
pega emprestado, é a quantia que se investe, é o
valor que se deve;
Juros (j) é o aluguel que se paga pelo capital, ou seja,
é o rendimento ou o acréscimo pago pelo
empréstimo de uma determinada quantia;
Montante (M) é a soma do capital com o juros.
Taxa de juros (i) é a porcentagem que se recebe de
rendimento em um investimento ou empréstimo de
uma quantia por certo tempo.
Tempo (t) é o período em que se investe ou
empresta certo valor, pode ser calculado em dias,
meses ou anos.

14. Nesta aula, aprendemos que juros
simples é o valor pago por um
empréstimo ao final do período de tempo
calculado apenas sobre o capital inicial,
mantendo-se constante durante todo o
tempo da transação.

15. Joaquim foi numa loja pagar uma fatura
no valor de R$ 550,00 com 4 dias de
atraso. Para o pagamento em atraso,
constava uma taxa de juros simples de
1% ao dia. Quanto Joaquim pagou?