1) O documento discute três tópicos: tratamento da informação, gráficos e dados estatísticos sobre vários temas como câmbio, pobreza, agricultura e saúde. 2) Há nove questões com gráficos ou tabelas e perguntas relacionadas sobre esses dados. 3) As questões abordam tópicos como análise e interpretação de dados, cálculos matemáticos e raciocínio lógico.

1. TRATAMENTO DA INFORMAÇÃO
1) (ENEM) No gráfico abaixo, mostra-se como variou o valor do dólar, em relação ao real, entre o final de
2001 e o início de 2005. Por exemplo, em janeiro de 2002, um dólar valia cerca de R$ 2,40. Durante esse
período, a época em que o real esteve mais desvalorizado em relação ao dólar foi no
a) final de 2001.
b) final de 2002.
c) início de 2003.
d) final de 2004.
e) início de 2005.
2) (ENEM) Analise o quadro acerca da distribuição da miséria no mundo, nos anos de 1987 a 1998.
A leitura dos dados apresentados permite afirmar que, no período considerado,
a) no sul da Ásia e na África Subsaariana está, proporcionalmente, a maior concentração da população
miserável.
b) registra-se um aumento generalizado da população pobre e miserável.
c) na África Subsaariana, o percentual de população pobre foi crescente.
d) em números absolutos a situação da Europa e da Ásia Central é a melhor dentre todas as regiões
consideradas.
e) o Oriente Médio e o Norte da África mantiveram o mesmo percentual de população miserável.
1

2. 3) Considerando os conhecimentos sobre o espaço
agrário brasileiro e os dados apresentados no gráfico, é
correto afirmar que, no período indicado,
a) ocorreu um aumento da produtividade agrícola devido
à significativa mecanização de algumas lavouras, como
a da soja.
b) verificou-se um incremento na produção de grãos
proporcionalmente à incorporação de novas terras
produtivas.
c) registrou-se elevada produção de grãos em virtude do
uso intensivo de mão-de-obra pelas empresas rurais.
d) houve um salto na produção de grãos, a partir de 91,
em decorrência do total de exportações feitas por
pequenos agricultores.
e) constataram-se ganhos tanto na produção quanto na produtividade agrícolas resultantes da efetiva reforma
agrária executada.
4) (ENEM) Em uma área observa-se o seguinte regime pluviométrico:
Os anfíbios são seres que podem ocupar tanto ambientes aquáticos quanto terrestres. Entretanto, há
espécies de anfíbios que passam todo o tempo na terra ou então na água. Apesar disso, a maioria das
espécies terrestres depende de água para se reproduzir e o faz quando essa existe em abundância. Os
meses do ano em que, nessa área, esses anfíbios terrestres poderiam se reproduzir mais eficientemente são
de
a) setembro a dezembro.
b) novembro a fevereiro.
c) janeiro a abril.
d) março a julho.
e) maio a agosto.
2

3. 5) (ENEM) A escolaridade dos jogadores de futebol nos grandes centros é maior do que se imagina,
como mostra a pesquisa abaixo, realizada com os jogadores profissionais dos quatro principais clubes de
futebol do Rio de Janeiro.
De acordo com esses dados, o percentual dos jogadores dos quatro clubes que concluíram o Ensino Médio é
de aproximadamente:
a) 14%
b) 48%
c) 54%
d) 60%
e) 68%
6) (ENEM) Os dados do gráfico foram coletados por meio da Pesquisa Nacional por Amostra de
Domicílios.
Supondo-se que, no Sudeste,
14 900 estudantes foram
entrevistados nessa pesquisa,
quantos deles possuíam
telefone móvel celular?
a) 5 513
b) 6 556
c) 7 450
d) 8 344
e) 9 536
3

4. 7) (ENEM) O gráfico expõe alguns números da gripe A-H1N1. Entre as categorias que estão em
processo de imunização, uma já está completamente imunizada, a dos trabalhadores da saúde.
De acordo com o gráfico, entre as demais categorias, a que está mais exposta ao vírus da gripe A-H1N1 é a
categoria de
a) indígenas.
b) gestantes.
c) doentes crônicos.
d) adultos entre 20 e 29 anos.
e) crianças de 6 meses a 2 anos.
8) (ENEM) Os dados do gráfico seguinte foram gerados a partir de dados colhidos no conjunto de seis regiões
metropolitanas pelo Departamento Intersindical de Estatística e Estudos Socioeconômicos (Dieese). Supondo
que o total de pessoas pesquisadas na
região metropolitana de Porto Alegre
equivale a 250000, o número de
desempregados em março de 2010,
nessa região, foi de
a) 24500.
b) 25000.
c) 220500.
d) 223000.
e) 227500.
4

5. 9) OBSERVE atentamente o gráfico que representa a distribuição do
número de horas diárias de sono de um conjunto de pessoas.
RESPONDA:
a) De quantas pessoas se registou o número de horas de sono?
b) Qual é o número de horas de sono mais frequente neste conjunto de
pessoas?
c) Neste estudo, quantas pessoas dormem menos de 8 horas?
d) Qual é a percentagem de pessoas do estudo que dormem mais de 8
horas?
e) JULGUE como verdadeira ou falsa cada uma das seguintes
afirmações. JUSTIFIQUE suas respostas:
( ) 50% das pessoas dorme mais do que 7,5 horas
( ) 25% das pessoas dorme menos do que 7 horas.
10) Em relação à notícia abaixo, ESCREVA um pequeno texto (10 linhas) com três informações significativas
retiradas dos gráficos.
5

6. CONJUNTO DOS NÚMEROS INTEIROS
1) Leia as manchetes e represente os valores com números negativos ou positivos.
..............................
...............................
................................
2) Veja no quadro abaixo as temperaturas médias registradas pelos termômetros em algumas cidades, num
determinado dia.
a) Nesse dia, Joana embarcou num avião em Porto Alegre e fez escala em São Paulo, rumo a Londres. Em
qual dessas três cidades a temperatura média era mais baixa? ......................................................
b) Em qual das cidades do quadro a temperatura média foi mais alta? ......................................................
3) Considere os pontos A, B, C, D e O sobre a reta numérica, na qual O é a origem, para responder as
questões seguintes.
a) D está relacionado a um número positivo ou negativo? ...............................................................
b) B é a imagem geométrica de qual número inteiro?.......................................................................
c) Qual é a abscissa do ponto C? .....................................................................................................
d) Dos pontos representados na reta acima, através das letras, quais são opostos? .....................
6

7. 4) RESPONDA o que se pede em cada item.
a) DETERMINE o módulo de +9 → ...............
b) I– 30I = ..............
c) Qual é o número de maior módulo: -6 ou +2? ....................
d) Qual é o valor de: I– 16I + I– 4I ? ...................
5) ASSINALE com V(verdadeiro) ou F (falso) cada afirmação.
a) ( ) O zero é maior que qualquer número negativo.
b) ( ) Qualquer número negativo é maior que qualquer número positivo.
c) ( ) O zero é menor que qualquer número positivo.
6) COMPLETE com os símbolos >, < ou = .
a) - 4 ...............+ 5
b) + 9.............. – 9
c) - 100........... – 1000
d) + 15 ............. 15
7) ASSINALE a sentença verdadeira.
a) 57 = – 57
b) 100 ≠ + 100
c) – 41 = + 41
d) –3 ≠+3
8) ASSINALE a sentença verdadeira.
a) - 12 > 4
b) - 12 > - 6
c) - 12 > 0
d) - 12 > - 20
9) ASSINALE a afirmativa verdadeira.
a) O produto de dois números inteiros negativos é um número negativo.
b) O quociente de dois números negativos é um número negativo.
c) A soma de dois números negativos é um número negativo.
d) A soma de dois números inteiros opostos é um número positivo.
7

8. 10) Uma pessoa tem R$ 600,00 em sua conta bancária e faz as operações abaixo. Qual é o seu saldo
final?
Retira R$ 73,00
Deposita R$ 180,00
Retira R$ 466,00
Retira R$ 125,00
________________________________________________________________________________________
11) CALCULE os valores das expressões seguintes.
a) (+ 14) + (– 5) + (+ 7) – (–11) =
b) 28 : (– 4) + 9 . (– 1) – 3 . ( 5 – 16) =
12) OBSERVE atentamente a figura e COMPLETE corretamente a pilha de números, seguindo o padrão
apresentado:
+1
+4
–5 +6 –2 –6
13) Fábio adicionou um número ao módulo dele e obteve zero como resultado. O número adicionado é
positivo ou negativo? ___________________________
14) Imagine uma cidade em que o termômetro está marcando 10°C depois de haver subido 7°C, baixado
5°C, subido outros 8°C e baixado 9°C. Qual era a temperatura inicial nessa cidade?
8

9. 15) Substitua a letra x pelo número inteiro que torna as sentenças verdadeiras.
a) (-84) : x = 4 x = ________
b) (-200 . x = 20 x = _________
c) |x| = 5 x = _________ ou x = _________
d) (x)3 = - 8 x = _________
e) x = 144 x = _________
16) COMPLETE corretamente o extrato bancário:
17) ASSINALE V nas sentenças verdadeiras e F nas falsas.
( ) -52 = ( -5 )2 ( ) ( -5 )2 = 52
( ) -23 = ( -2 )3 ( ) -27 = ( - 2 ) 7
18) CALCULE:
a) ( -2 )4 = _________ b) 1010 = _________
c) ( -49 )1 = _________ d) 169 = _________
19) RESOLVA as expressões:
a) ( -54 ) : ( -6 ) – 72 : 9 + 36 : ( - 12 ) + 8
2
b) 32 . (– 2)5 + (– 3)2 – 25
9

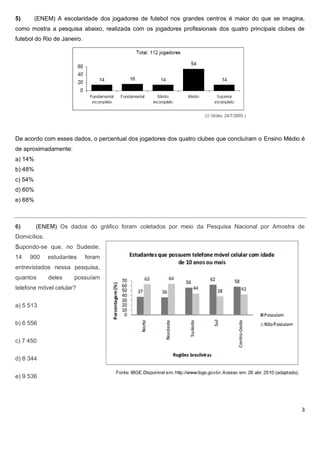
10. 20) O gráfico mostra os lucros de uma companhia de seguros nos quatro primeiros meses de 2010.
a) Nesse período, a empresa teve lucro positivo ou negativo? _______________
b) De quanto? _______________
________________________________________________________________________________________
21) COMPLETE corretamente a sequência:
22) Imagine que x e y sejam números negativos. Nesse caso, efetuando x.y.x:y obtém-se como resultado um
número:
a) negativo.
b) positivo.
c) nem positivo nem negativo.
d) nulo.
23) O resultado da expressão 13 – [ 3 . ( -5 ) ] é:
a) -2 b) 2 c) 28 d) -28
24) ASSINALE a alternativa falsa.
a) O oposto de -10 é 10.
b) O módulo de +15 é 15.
c) O antecessor de -10 é -9.
d) O sucessor de +15 é +16.
10

11. 25) O valor da expressão (– 12) : (+ 2) . (– 2 – 3 – 5) é
a) 16. b) 60. c) – 16. d)– 60.
26) ASSINALE a sentença verdadeira.
a) (– 2)2 = – 4 b) (– 3)2 = (+ 3)2 c) – 22 = 4 d) (– 2)1 = 2
27) Se a = 3 e b = – 5, então a2 +2ab + b2 é:
a) – 46. b) 4. c) 19. d) 64.
28) CALCULE:
a) (+ 28) + (+17) = ___________ d) (+ 10) – ( + 3) = ___________
b) (+3) . (– 5) = ___________ e) (– 40) : (– 4) = ___________
c) (– 2) – (– 7) = ___________ f) (– 8)2 = ___________
________________________________________________________________________________________
29) ASSOCIE corretamente V(verdadeiro) ou F(falso) a cada afirmação (você deve fazer os cálculos para
verificar se a sentença está verdadeira ou falsa).
a) ( ) – 2 + 8 > -2 + 7
b) ( ) 3 + (– 4) > 5 + (– 5)
c) ( ) –10 + 4 > –18 + 12
30) Em um quadrado mágico, as somas na horizontal, na vertical e na diagonal são todas iguais.
Determine os números que faltam para se obter um quadrado mágico na figura.
31) CALCULE o valor da seguinte soma algébrica: – (– 3 ) + { – [ ( + 8 ) + (– 10 ) ] + (– 5 ).
11

12. 32) CALCULE o valor dos produtos:
a) 7 . (–1 ) . ( + 10 ) . ( +2 ) =
b) (– 3 ) . (– 5 – 7 ) =
33) CALCULE o valor das seguintes divisões:
a) ( + 45 ) : (– 15 ) = b) (– 48 ) : (– 48 ) = c) 160 : (– 20 )= d) 0 : ( + 9 ) =
34) O valor da expressão (– 50) : (–10 ) : 5 é:
a) 1 b) 25 c) –1 d) –25
35) CALCULE:
a) (– 8 )2 = b) (+ 3 )3 = c) (– 2 )5 = d) (+ 7 )0 = e) (– 4 )1=
36) REDUZA a uma só potência, aplicando as propriedades da potenciação:
a)(– 3 )4 . (– 3 ) . (– 3 )3 =
b) ( + 14 )8 : ( + 14 )6 =
c) [ ( - 6 ) 6 ] 3 =
37) CALCULE o valor da expressão: (– 3 )2 + 5 0 – (– 2 )4 ?
38) DETERMINE o valor de:
a) - 121 b) 64 c) - 81
39) RESPONDA: que número inteiro deve ser colocado no lugar de x para que sejam verdadeiras as
igualdades?
a) x . ( + 3 ) = – 6 → x = ..............
b) x : ( + 3 ) = + 5 → x = ..............
c) ( x ) 3 = – 8 → x = ..............
d) (– 3 ) + x = – 18 → x = ..............
40) CALCULE o valor de:
a) A 100 b) B 1 9 4 c) A B
12

13. CONJUNTO DOS NÚMEROS RACIONAIS
1) ASSINALE a alternativa correta:
3 1
a) 5 IN b IN Z 16 Q
7 c) 2 d)
19
2) Simplificando a fração obtemos:
38
1 1
a) – 2 b) c) 2 d)
2 2
________________________________________________________________________________________
3) ESCREVA os valores correspondentes às quantias:
4) ESCREVA as frações decimais na forma de números decimais:
228 98 1336 61 129
a) b) c) d) e)
10 1000 1000 000 100 10 000
____________________________________________________________________________________
5) ESCREVA cada um dos números a seguir na forma de fração decimal:
a) 14,3 b) 0,016 c) 0,276 d) 2,203 e) 1,405
13

14. 6) Usando algarismos, escreva na forma decimal:
a) quatro inteiros e sete décimos d) dois inteiros e trezentos e cinqüenta e um
centésimo de milésimos
b) dois inteiros e trinta e cinco milésimos
e) sete inteiros e oito centésimos de milésimo
c) quarenta e sete centésimos
7) Usando os sinais = , > ou < , compare os seguinte decimais:
a) 8,69 _______ 9,1 e) 2,08 _______ 2,0095
b) 28,11 _______ 28,108 f) 5,09 _______ 5,3
c) 0,09500 _______ 0,095 g) 10,02 _______ 10,0075
d) 49,02 _______ 45,8 h) 4,03 _______ 4,0300
8) Escala Richter - A quantidade de energia liberada por um terremoto é medida pela escala Richter. De
forma geral, terremotos com magnitudes até 3,5 ou menos são raramente percebidos; de 3,5 a 6,0 são
sentidos e causam poucos danos, entre 6,1 e 6,9, podem ser destrutivos e causar danos em um raio de cem
quilômetros do epicentro; entre 7,0 e 7,9, causam danos sérios em áreas maiores; e de 8,0 em diante são
destrutivos por um raio de centenas de quilômetros.
Sandra e Paulo estão pesquisando e respeito dos superterremotos de 8,0 ou mais na escala Richter. Na
tabela baixo estão alguns locais onde ocorreu esse tipo de catástrofe.
Terremotos
Data Local Pontos na escala Richter
1755 Lisboa (Portugal) 8,75
1906 São Francisco (EUA) 8,3
1950 Assan (Índia) 8,7
1977 Indonésia 8,0
1985 Cidade do México (México) 8,1
RESPONDA: Em qual desses lugares ocorreu o terremoto mais arrasador e o menos? ESCREVA os locais
onde os terremotos aconteceram em ordem decrescente.
9) Construa uma reta numérica e localize os seguintes números:
1 1 2 2 1 1
a) e b) e c) e
3 3 5 5 2 5
14

15. 10) Localize os números abaixo na reta numérica que você construiu:
a) + 1,2 e - 1,2
b) + 5,6 e - 5,6
c) + 7,4 e - 7,4
11) Copie a listagem de números abaixo ordenando-os do menor para o maior:
12) Na reta numérica, entre os números 0 e 1 existe:
a) um número finito de números racionais?
b) um número infinito de números racionais?
b) E em outros intervalos como, por exemplo, entre 1 e 2?
13) Relacione cada número indicado na primeira coluna com o intervalo da reta numérica em que ele se
localiza:
14) Registre dois procedimentos que ajudam a localizar números racionais escritos na forma decimal, na
reta numérica.
15) Lembrando da localização de números racionais na reta numérica, compare cada par de números e
coloque entre eles os símbolos > ou <:
1 1 2 5
a) ..........
..... d) ..........
.....
2 3 3 3
1 1 2 5
b) ..........
..... e) ..........
.....
2 3 3 3
1 1 2 5
c) ..........
..... f) ..........
.....
2 3 3 3
15