Carregado porAlvaro Augusto
Teoria dos jogos
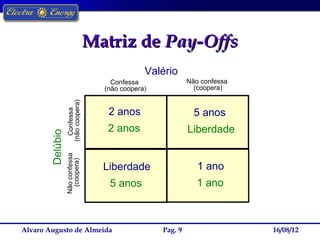
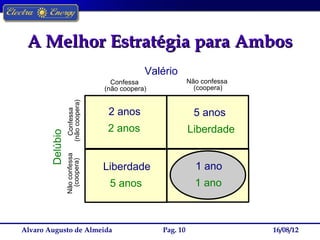
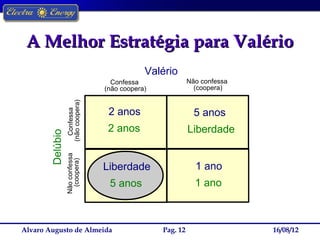
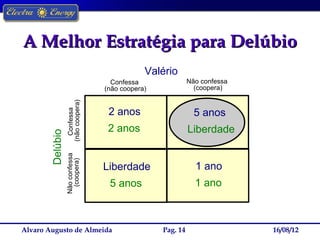
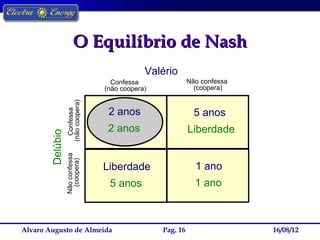
A Teoria dos Jogos estuda as interações estratégicas entre agentes em situações formais. O documento descreve o dilema do prisioneiro, no qual a melhor estratégia individual leva a um resultado ruim para ambos, e como a estratégia de "olho por olho, dente por dente" levou à cooperação em torneios repetidos.
Mais conteúdo relacionado
Teoria dos jogos
- 1. Teoria dos Jogos f Alvaro Augusto de Almeida Pag. 1 16/08/12
- 2. Tudo está emJogo! • A Teoria dos Jogos é um ramo da Matemática Aplicada que usa modelos para estudar as interações entre agentes (jogadores) em estruturas formais de incentivo (jogos). Alvaro Augusto de Almeida Pag. 2 16/08/12
- 3. Os Jogos • Osjogos em questão podem ser de várias formas: – Relações interpessoais. – Relações econômicas. – Estratégias militares, de caça e de negociação. – Comportamento animal (etologia). Alvaro Augusto de Almeida Pag. 3 16/08/12
- 4. Jogos Mais Interessantes •No contexto da Teoria dos Jogos, os jogos mais interessantes são aqueles que induzem a raciocínios do tipo: “o que será que ele está pensando sobre o que eu estou pensando que ele está pensando?” Alvaro Augusto de Almeida Pag. 4 16/08/12
- 5. Jogos de SomaZero • John von Neumann e Oskar Morgenstern, 1944. • Jogos de “Soma Zero”: o ganho de um jogador é igual à perda do outro. • Ex.: xadrez, pôquer. Alvaro Augusto de Almeida Pag. 5 16/08/12
- 6. Jogos de SomaNão Zero • John Nash, 1950. • Jogos de “Soma Não Zero”: os ganhos dos jogadores são não nulos. • Equilíbrio de Nash. Alvaro Augusto de Almeida Pag. 6 16/08/12
- 7. Dilema do Prisioneiro • Protótipo para jogos de soma não zero. • Cada jogador tenta maximizar os seus resultados, sem conhecimento das escolhas do outro jogador. Alvaro Augusto de Almeida Pag. 7 16/08/12
- 8. Estrutura do Dilemado Prisioneiro • Dois ladrões cometem um crime em conjunto e são capturados. • A polícia interroga cada um deles separadamente e oferece as seguintes opções: – Se ficarem calados (cooperação), ambos são condenados a um ano de cadeia; – Se ambos confessarem (falta de cooperação), ambos são condenados a dois anos; – Se apenas um confessar (traição), aquele que confessou ganha liberdade (“delação premiada”), e o outro é condenado a cinco anos . Alvaro Augusto de Almeida Pag. 8 16/08/12
- 9. Matriz de Pay-Offs Valério Confessa Não confessa (não coopera) (coopera) (não coopera) 2 anos 5 anos Confessa 2 anos Liberdade Delúbio Não confessa (coopera) Liberdade 1 ano 5 anos 1 ano Alvaro Augusto de Almeida Pag. 9 16/08/12
- 10. A Melhor Estratégiapara Ambos Valério Confessa Não confessa (não coopera) (coopera) (não coopera) 2 anos 5 anos Confessa 2 anos Liberdade Delúbio Não confessa (coopera) Liberdade 1 ano 5 anos 1 ano Alvaro Augusto de Almeida Pag. 10 16/08/12
- 11. A Melhor Estratégia? •A Estratégia anterior depende de absoluta confiança entre os dois ladrões. Mas, se eles são ladrões... • Assim, rapidamente Valério perceberá que pode trair Delúbio e sair em liberdade. Alvaro Augusto de Almeida Pag. 11 16/08/12
- 12. A Melhor Estratégiapara Valério Valério Confessa Não confessa (não coopera) (coopera) (não coopera) 2 anos 5 anos Confessa 2 anos Liberdade Delúbio Não confessa (coopera) Liberdade 1 ano 5 anos 1 ano Alvaro Augusto de Almeida Pag. 12 16/08/12
- 13. Problemas • O problemaé que Valério não sabe o que Delúbio fará. • Ocorre que Delúbio também chegou à conclusão que é melhor trair Valério e sair em liberdade... Alvaro Augusto de Almeida Pag. 13 16/08/12
- 14. A Melhor Estratégiapara Delúbio Valério Confessa Não confessa (não coopera) (coopera) (não coopera) 2 anos 5 anos Confessa 2 anos Liberdade Delúbio Não confessa (coopera) Liberdade 1 ano 5 anos 1 ano Alvaro Augusto de Almeida Pag. 14 16/08/12
- 15. A Melhor Estratégiacom Restrições • Como Valério não sabe o que Delúbio fará, e vice-versa, a informação é restrita. • A “melhor” solução, que levará ao equilíbrio de Nash, ocorre quando ambos os jogadores tentam maximizar seus resultados, traindo o companheiro. Alvaro Augusto de Almeida Pag. 15 16/08/12
- 16. O Equilíbrio deNash Valério Confessa Não confessa (não coopera) (coopera) (não coopera) 2 anos 5 anos Confessa 2 anos Liberdade Delúbio Não confessa (coopera) Liberdade 1 ano 5 anos 1 ano Alvaro Augusto de Almeida Pag. 16 16/08/12
- 17. Dilema do Prisioneirocom Repetição • As coisas mudam quando o jogo é repetido, como acontece na vida real. • Quando os jogadores voltarem a se encontrar, saberão que não podem confiar um no outro. • Qual a melhor estratégia, então? Alvaro Augusto de Almeida Pag. 17 16/08/12
- 18. Os Torneios deAxelrod • Robert Axelrod é professor de Ciência Política na Universidade de Michigan. • Em 1984, ele organizou um torneio cibernético onde os parcipantes deveriam apresentar estratégias para o Dilema do Prisioneiro Iterado. Alvaro Augusto de Almeida Pag. 18 16/08/12
- 19. Tit for Tat •A estratégia vencedora foi a Tit for Tat, nome que deriva da expressão Tip for Tap, que significa “retaliação equivalente”. • Tit for Tat inicia cooperando, e depois imita a atuação do adversário: – Se o adversário cooperou, Tit for Tat coopera; – Se o adversário traiu, Tit for Tat trai. Alvaro Augusto de Almeida Pag. 19 16/08/12
- 20. Características de Titfor Tat • Tit for Tat é transparente: após algumas jogadas, qualquer adversário percebe qual é a estratégia; • Tit for Tat não guarda rancor; • Tit for Tat é rápida na retaliação; • Tit for Tat implica no estabelecimento de uma reputação. Alvaro Augusto de Almeida Pag. 20 16/08/12
- 21. O Papel da“Banca” • Todo jogo de soma não zero pode ser transformado em um jogo de soma zero, bastando adicionar-se um jogador extra, que assume o ganho ou prejuizo: a “banca”. • No caso do Dilema do Prisioneiro, por exemplo, os prisioneiros perdem, mas alguém ganha. Quem? Alvaro Augusto de Almeida Pag. 21 16/08/12
- 22. Jogos com MútiplosParticipantes • Quando mais de um participante faz parte do jogo, o Dilema do Prisioneiro evolui para a Tragédia dos Comums. Alvaro Augusto de Almeida Pag. 22 16/08/12
- 23. A Tragédia dosComuns • Na Inglaterra medieval, não havia propriedade privada, no sentido atual deste termo. • Havia somente as propriedades dos reis e nobres, onde a caça e o pasto eram proibidos, e os terrenos baldios (“commons”), de uso comum. • A Tragédia dos Comuns surge quando os camponeses, que levavam as vaquinhas para pastar, tentavam maximizar os resultados individuais, em detrimento do bem comum. Alvaro Augusto de Almeida Pag. 23 16/08/12
- 24. Exemplos de Tragédiados Comuns • Jantar ou almoço comunitário, com equipartição das despesas (rateio). • Crescimento populacional descontrolado. • Consumo de combustível fóssil. • Pesca em águas internacionais. • Envio de e-mails não solicitados (spam). • Conta de Resultados a Compensar (CRC). Alvaro Augusto de Almeida Pag. 24 16/08/12
- 25. Solução para aTragédia dos Comuns • Quando for possível, privatize o pasto. • Quando não for possível, cobre multas. • Quando nada disso der certo, chore! Alvaro Augusto de Almeida Pag. 25 16/08/12
- 26. O Dilema doLobo • Variação interessante da Tragédia dos Comuns. • Várias pessoas são convidadas a ficar 15 minutos dentro de uma cabine individual, dentro da qual há um botão que aciona uma campainha. • Se ninguém apertar o botão, cada participante ganha R$ 1.000. • Se alguém apertar o botão, aquele que apertou ganha R$ 100, e os outros não ganham nada. • Qual o resultado do experimento? Alvaro Augusto de Almeida Pag. 26 16/08/12
- 27. O Dilema doLobo de Verdade • Lobos caçam em grupos, usando uma estratégia coletiva e dividindo a caça de acordo com uma hierarquia rígida. • De vez em quando, um lobo acaba pensando ser o único responsável pela caça e tenta apropriar-se integralmente dela. Alvaro Augusto de Almeida Pag. 27 16/08/12
- 28. Solução para oDilema do Lobo • Puna o lobo • Expulse-o da matilha! Alvaro Augusto de Almeida Pag. 28 16/08/12
- 29. O Leilão daNota de US$ 1,00 • O leilão da nota de US$ 1,00 foi proposto por Martin Schubik, que usou estudantes universitários como cobaia. • Leilão clássico: – Uma nota de US$ 1,00 é posta em leilão. – Qual será o lance máximo ofertado por ela? Alvaro Augusto de Almeida Pag. 29 16/08/12
- 30. Leilão Modificado • Anota de US$ 1,00 é posta em leilão. • O maior lance paga e leva a nota, mas... • O segundo maior lance paga, mas não leva. • Coalisões são proibidas. • Qual o resultado? Alvaro Augusto de Almeida Pag. 30 16/08/12
- 31. Sunk Costs • Quandonão há mais esperanças de ter lucro, as pessoas tentam minimizar o prejuízo. • Os custos incorridos nessa situação são denominados Sunk Costs (Custos Afundados). • Quando ainda há esperanças de recuperar os custos, os economistas falam em Stranded Costs (Custos Encalhados). Alvaro Augusto de Almeida Pag. 31 16/08/12
- 32. Conclusões “É melhor serum chacal vivo do que um leão morto, mas é ainda melhor ser um leão vivo!” Robert Heinlein Alvaro Augusto de Almeida Pag. 32 16/08/12
- 33. FIM! Alvaro Augusto deAlmeida Pag. 33 16/08/12