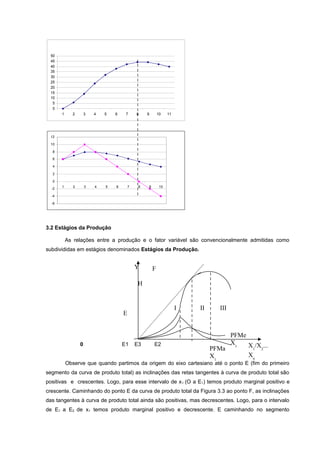
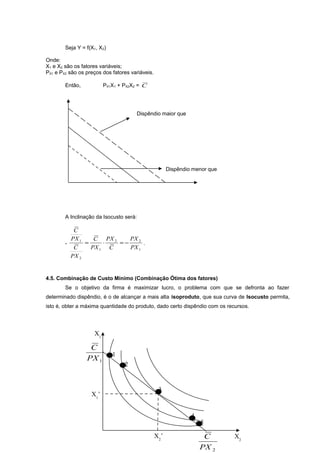
Este documento fornece uma introdução à teoria da produção, discutindo conceitos-chave como empresa, produção, processos produtivos, fatores de produção, curto e longo prazo, funções de produção, eficiência técnica e econômica, estágios da produção e determinação da quantidade ótima do fator variável. O documento destaca a importância de entender esses conceitos para analisar custos, oferta, preços e alocação de recursos na economia.

1. UNIVERSIDADE FEDERAL DO CEARÁ
CENTRO DE CIÊNCIAS AGRÁRIAS
DEPARTAMENTO DE ECONOMIA AGRÍCOLA
DISCIPLINA: TEORIA ECONÔMICA APLICADA
Teoria da Produção
Francisco Casimiro Filho
Professor Adjunto III – DEA/CCA/UFC
1. INTRODUÇÃO
A Teoria da Firma é a parte da microeconomia que se preocupa em estudar o comportamento
da firma. Esse tópico foi pouco abordado até agora, sendo que apresentamos apenas a curva de
oferta de mercado A Teoria da Firma é a parte da Economia que engloba a Teoria da Produção,
Teoria dos Custos de Produção e os Rendimentos da Firma.
Na Teoria da Produção a unidade econômica em estudo e a firma ou empresa. Assim esta
teoria visa proporcionar ao produtor a base racional necessárias para suas decisões, com relação à
produção, que é precondição para se chegar a oferta.
A importância do estudo da Teoria da Produção reside no fato de que:
•
seus princípios gerais proporcionam as bases para a análise dos custos e da oferta dos bens
produzidos; e
•
seus princípios, também, se constituem peças fundamentais para a análise dos preços e do
emprego dos fatores de produção, bem como da alocação desses fatores entre os diversos
usos alternativos na economia.
Para um melhor entendimento temos que explicitar, inicialmente, alguns conceitos básicos da
Teoria da Produção, que são apresentados a seguir
2. CONCEITOS BÁSICOS
2.1 Empresa ou Firma
É uma unidade técnica que produz bens e/ou serviços de forma racional, procurando
maximizar seus resultados relativos a produção e o lucro. Esse conceito abrange um
empreendimento de modo geral, que inclui as atividades industriais e agrícolas, as
atividades
profissionais, técnicas e de serviços. Assim, é uma firma um mecânico de automóveis, um barbeiro,
um médico, uma loja de confecções etc.
2.2. Produção
É o processo pelo qual uma firma transforma os fatores de produção em produtos e serviços.
Insumos
Mão-de-obra
Capital
Terra
Processo de
Produção
Produto

2. 2.3 Processo de Produção
É a técnica por meio da qual um ou mais produtos vão ser obtidos a partir da utilização de
determinadas quantidades de fatores de produção.
2.4. Fatores de Produção
Os fatores de produção são bens ou serviços transformáveis em produção, e se dividem
em:
•
fatores de produção primários - são os fatores naturais, que existem
independentemente da ocorrência de um processo produtivo anterior. Exemplo de
fator de produção primário é a terra; e
•
fatores de produção secundários - são aqueles que necessitam de um
processo produtivo anterior para criá-los. Exemplo de um fator de produção
secundário são as máquinas;
Os fatores de produção também podem ser classificados considerando uma distinção
puramente temporal em:
Fatores fixos: São aqueles cuja quantidade utilizada não se modifica, embora se altere a
quantidade produzida do produto. Ex: mão-de-obra permanente (contratada) beifeitorias etc.
Fatores variáveis: São aqueles em que a quantidade varia com a variação na quantidade
produzida do produto. Ex: semente, adubo, mão-de-obra etc.
2.5 Curto Prazo e Longo Prazo
a) Curto prazo: É o período de tempo no qual existe pelo menos um fator de produção fixo.
Y = f(X1/X2, X3,... , Xn)
b) Longo prazo: É o período de tempo no qual todos os fatores de produção variam.
Y = f(X1, X2, X3,... Xn)
2.6. Funções de Produção
É a relação técnica entre as quantidades físicas produzidas de determinado produto e as
quantidades fisicas dos fatores empregados na sua produção em determinada unidade de tempo.
Ex: milho→ terra, trabalho, semente, fertilizante etc.
A função de produção pode ser representada por:
Y = f(X1, X2, X3,... Xu),
onde:
Y = quantidade máxima produzida do bem, sendo q > 0 e
X1 , X2, ..., Xn são as quantidades utilizadas dos diversos fatores de produção, sendo xi > 0 (i
= 1, 2, ..., n).

3. i) O nível de produção depende de técnicas de produção utilizada (tenologia)
ii) O nível de produção depende dos níveis de uso dos fatores (alocação).
Admitir-se-á que o produtor utilizará a mais eficiente tecnologia, assim, o problema tornar-seá apenas um problema de alocação dos insumos.
2.7. Eficiência técnica e a eficiência econômica
Na teoria de produção há ainda dois conceitos, a saber, os quais fazem a diferença entre
empresas ou firmas e em cooperativas. A eficiência técnica e a eficiência econômica são meios
pelos quais afetam a produção.
A eficiência técnica envolve aspectos físicos da produção. Assim, a produção é tecnicamente
eficiente quando não há a possibilidade de substituir um processo produtivo por outro capaz de obter
o mesmo nível de produção com uma quantidade inferior de insumos, exemplo: Se para produzir 10
ton de feijão são necessários 100 Kg de sementes e 10ha, e se verificar que utilizando 90Kg de
sementes não afeta na produção com a mesma área, desta forma podemos dizer que houve uma
eficiência técnica.
A eficiência econômica envolve os aspectos monetários da produção de modo a conduzir o
processo produtivo de forma a deter máximo lucro ou menor custo.
Para entender melhor esses conceitos consideremos oseguinte exemplo suponha que temos
uma fazenda de 100 hectares, dos quais 80 são aptos ao plantio de milho.
A fazenda é uma firma. Os 80 hectares de terra
adequados ao plantio de milho, o trabalho utilizado, as
sementes, os inseticidas, os corretivos de solo etc., são os
fatores de produção. Esses serão combinados, através de
determinada técnica, para gerar a produção de milho.
Existem várias técnicas de plantio de milho, sementes por metro linear, agrotóxicos,
variedades etc. Cada uma dessas técnicas é um processo de produção. A função de produção
considera o processo de produção que permite obter o máximo produto a partir de certa quantidade
de fatores de produção.
Portanto, a função de produção indica o máximo de produto que se pode obter com
as quantidades dos fatores, uma vez escolhido determinado processo de produção mais
conveniente.
3. FUNÇÃO DE PRODUÇÃO COM UM FATOR VARIÁVEL ou Relação Fator-Produto (Análise de
curto prazo)
Consideremos uma função de produção com apenas dois fatores de produção, sendo um
fixo (que não varia com a realização do processo produtivo) e outro variável:
q = f(x1, x 2),
onde: q = quantidade de produto;

4. x1 = fator variável; e
x2 = fator fixo;
Esta relação se fundamenta na Lei dos Rendimentos Decrescentes ou Lei das
Proporções Variáveis que diz:
“Quando aumentamos a quantidade do fator variável, mantendo as demais constantes, a
produção aumenta inicialmente a taxas crescentes, depois a taxas decrescentes, atinge um máximo e
finalmente decresce”.
Três pontos devem ser ressaltados na Lei dos Rendimentos Decrescentes:
a) só ocorre quando temos apenas um fator variável e todos os demais fixos;
b) ocorre devido a uma alteração nas proporções da combinação entre os fatores e
c) foi considerada por Ricardo como válida para a agricultura e generalizada pelos
Neoclássicos para toda a economia.
Devido a Lei dos Rendimentos Decrescentes, a curva do produto total é formada de três
segmentos: o primeiro é convexo em relação ao eixo de x 1, o segundo é côncavo em relação ao eixo
de x1 e o terceiro tem inclinação negativa (Figura 5.1).
3.1. Conceito de Produção Total, Produtividade Média e Produtividade Marginal
3.1.1 Produção Total (PT)
Representa as máximas quantidades do produto (Y) que podem ser obtidas a determinados
níveis de usos do insumo (mediante adequada escolha do processo produtivo).
Figura 3.1. Função de produção e alterações na proporção dos fatores fixos e variáveis
Como um exemplo, considere que q é a quantidade produzida de milho, x 1 é a quantidade
utilizada de fertilizantes e x 2 é a área plantada (igual a 80 hectares). A quantidade do produto (q)
altera à medida que x1 muda sua magnitude.
A partir da curva de PT podemos derivar as curvas de PMe X1, PMaX1 que são conceitos
bastante importantes na tomada de decisão pela firma com respeito ao uso dos fatores.

5. 3.1.2 Produtividade Média do Fator Variável
Relação entre o nível do produto e a quantidade do fator de produção, num determinado
período de tempo:
Exemplos:
- Produtividade média da mão-de-obra:
PMe m.o. =
PT
(é o produto por trabalhador)
m.o.
- Produtividade média do capital:
PMe K =
PT
( é o produto pelo capital empatado)
K
- Produtividade média da terra:
PMeT =
PT
(é a produção por hectare)
T
3.1.3 Produtividade Marginal do Fator Variável
É a variação no PT decorrente da variação na quantidade do fator, num determinado período
de tempo.
PMa x1 =
∆PT
∆Y
=
no arco
∆X 1
∆X 1
PFMa x1 =
dY
no ponto
dX 1
Exemplo:
Fator Fixo
X2
10
10
10
10
10
10
10
10
10
10
10
Fator Variável
X1
0
1
2
3
4
5
6
7
8
9
10
Produção Total
Y
0
6
14
24
32
38
42
44
44
42
40
Y/X1
∆Y/∆X1
6
7
8
8
7,6
7,0
6,2
5,4
4,6
4,0
6
8
10
8
6
4
2
0
-2
-4

6. 50
45
40
35
30
25
20
15
10
5
0
1
2
3
4
5
6
1
2
3
4
5
7
6
8
9
10
11
12
10
8
6
4
2
0
-2
7
8
9
10
-4
-6
3.2 Estágios da Produção
As relações entre a produção e o fator variável são convencionalmente admitidas como
subdivididas em estágios denominados Estágios da Produção.
Y
F
H
I
E
0
E1
E3
E2
II
III
PFMe
X1
X1/X2...
PFMa
Xn
X1
Observe que quando partimos da origem do eixo cartesiano até o ponto E (fim do primeiro
segmento da curva de produto total) as inclinações das retas tangentes à curva de produto total são
positivas e crescentes. Logo, para esse intervalo de x 1 (O a E1) temos produto marginal positivo e
crescente. Caminhando do ponto E da curva de produto total da Figura 3.3 ao ponto F, as inclinações
das tangentes à curva de produto total ainda são positivas, mas decrescentes. Logo, para o intervalo
de E1 a E2 de x1 temos produto marginal positivo e decrescente. E caminhando no segmento

7. decrescente da curva de produto total temos inclinações negativas das tangentes à curva de produto
total. Logo, a partir de E2 o produto marginal é negativo.
No segmento OH da curva de produto total, os raios que ligam cada ponto da curva de
produto total à origem do eixo cartesiano têm inclinações ascendentes, mas menores do que as
inclinações das retas tangentes à curva de produto total nesses pontos. Logo, o produto médio é
crescente, mas menor do que o produto marginal. No ponto H da curva de produto total, o raio que
liga esse ponto à origem do eixo cartesiano também é tangente à curva de produto total. Logo, no
ponto H da curva de produto total, o produto médio e o produto marginal são iguais. A partir do ponto
H da curva de produto total, as inclinações dos raios que ligam esses pontos até a origem do eixo
cartesiano são positivas, mas decrescentes. Esses raios têm inclinações maiores do que as
tangentes à curva de produto total. Logo, a partir de E 3 o produto médio é positivo, mas decrescente,
e maior do que o produto marginal.
O segmento OH da curva de produto total da Figura 3.3 é chamado de estágio I da função de
produção (é o segmento onde o produto médio é crescente). O segmento HF da curva de produto
total é chamado de estágio II da função de produção. E o segmento a partir de F da curva de
produto total é chamado de estágio III da função de produção.
Estágio I:
Y↑
Y/X1 ↑
 Y
∆Y/∆X1 (crescente e decrescente) Termina quando 
X
 1




max
=
∆Y
∆X 1
Estágio II:
Y↑
Y/X1 ↓
 Y
Começa quando 
X1

∆Y/∆X1 ↓ > 0
max
max
=
Termina quando (Y )
Estágio III:
Y↓ > 0
Y / X1 ↓
∆Y / ∆X1 < 0




Começa quando
=
∆Y
∆X 1
∆Y
=0
∆X
∆Y
=0
∆X 1
Onde deveria (em qual estágio) o empresário racional produzir? O empresário deveria
produzir no estágio II que é o estágio racional de produção.
Obs: “A localização do nível de uso de insumo no estágio II, dependerá dos preços dos fatores fixos e
do preço do fator variável”.
3.3. Determinação da Quantidade Ótima do Fator Variável a se Empregar
Sabemos que um dos objetivos do empresário é maximizar lucros.
Matematicamente:

8. Seja a função física de produção:
Y = f(X1/X2 ... Xn)
Receita Total ou Bruta = Y . Py
Custos = X1 PX1 + K (Custo dos fatores fixos)
Receita líquida (RL) = Y . Py – (X1 PX1 + K)
A RL para ser máxima deve satisfazer as seguintes condições:
a)Condição necessária ou de 1ª ordem
dy PX 1
dL
dY
=
⋅ Py − PX 1 = 0 ∴
⋅
dX 1 dX 1
dX 1 Py
PFMa =
PX 1
.
PY
b)Condição suficiente ou de 2ª ordem
d 2L
dX 1
2
Logo
=
d2y
dX 1
d 2Y
dX 1
2
2
⋅ Py < 0
< 0.
Exemplo:
Dada a função de produção Y = 12 + 0,44X 1 – 0,0005X12 onde Y representa peso vivo de carne
suína em Kg e X1 quantidade de ração (milho mais concentrado protéico/em Kg. Considere que o
custo da ração seja 3,00 u.m./Kg e o preço da carne 15,00u.m./Kg. Pede-se:
a) Qual a quantidade de ração que proporcione a máxima produção de carne? (máxima
eficiência técnica)
b) Qual a quantidade de ração que proporciona o máximo lucro? (máxima eficiência econômica)
c) Admitindo-se que o custo dos fatores fixo é da ordem de 100,00 u.m. determine o lucro em
(a) e em (b)
Solução:
a) Y = 12 + 0,44X1 – 0,0005X12
Ymax → PFMaX1 = dY/dX1 = 0
dY
= 0,44 + 0,0010 X 1 = 0
dX 1

9. X1 = 440Kg de ração.
b) Lmax = PFMaX1 = PX1/Py
0,44 − 0,0010 X 1 =
3,00
∴0,44 − 0,2 = 0,0010 X 1
15,00
X1 = 240Kg de ração.
c) Cálculo da Produção
c1) Para X1 = 440Kg de ração
Y = 12 + 0,44X1 – 0,005X12 = 12 + 0,44(440) – 0,0005(440)2 = 108,8Kg de carne
de porco
L = RT – CT = YPy – (X1PX1 + K)
L = (108,8 x 15,00) – (440 x 300 – 10.000) = 163.200 – 142.000 = 212 u.m.
L = 212 u.m.
c2) Para X1 = 240Kg de ração
Y = 12 + 0,44X1 – 0,0005X12
Y = 12 + 0,44 (240) – 0,0005 (240)2 = 12 + 105,6 – 28,8 = 88,8Kg de carne de porco
Y = 88,8 Kg de carne de porco.
L = YPy – X1PX1 – K
L = 88,8 x 15,00 – 240 x 3,00 – 10.000
L = 51.200u.m.
3.4 Elasticidade da Produção
É um conceito importante para tomada de decisões ao nível da firma, já que mostra
mudanças percentual na produção derivada de movimentos percentuais no fator variável.
Dada: Y = f(X1/X2... Xn)
Ey =
Então
Variável Percentual na Produção (Y)
Variável Percentual no Fator Variação (X1)
∆Y
∆%Y
∆Y X 1 PFMaX 1
= Y =
⋅
=
Ey =
∆% X 1 ∆X 1 ∆X 1 Y
PFMeX 1
X1
∆Y X 1
⋅
→ (no arco), isto é, elasticidade média da produção
Ey =
∆X 1 Y
Ey =
dY X 1
⋅
dX 1 Y
→ (no ponto).

10. 3.4.1.Relação entre a Elasticidade da produção e os estágios da produção
Ey =
∆Y X 1 ∆Y / ∆X 1 PFMaX 1
⋅
=
=
∆X 1 Y
Y / X1
PFMeX 1
Estágio I
PFMaX1 > PFMeX1 → Ey > 1
Fim do I estágio e começo do II → PFMaX1 = PMeX1 → Ep = 1 1
Estágio II
PMaX1 < PMeX1 → Ey < 1
Fim do II estágio e começo do III → PMaX1 = 0 → Ep = 0
Estágio III → PFMaX1 < 0 → Ey < 0.
4. FUNÇÃO DE PRODUÇÃO COM DOIS FATORES VARIÁVEIS -Relação FATOR – FATOR
Vamos considerar que todos os fatores de produção são variáveis, ou seja, façamos a análise
no longo prazo. Para permitir um tratamento geométrico considere apenas dois fatores variáveis:
Esta relação pode ser expressa da seguinte forma:
Y = f(X1, X2 / X3, X4 ... Xn)
F.V.
F.F.
Nestas condições, da mesma maneira que na teoria do consumidor, aqui há possibilidade
de substituição de um fator por outro e a curva representando o mesmo nível de produção para
diferentes combinações pode ser derivada da mesma forma que a curva de indiferença.
“Uma função de produção com estas características pode ser determinada por uma curva
denominada isoquanta”.
X1
(farinha
de carne)
Isoquanta – é uma linha que mostra diferentes combinações de 2 fatores (X 1 e X2) que indicam a
mesma quantidade produzida.
As isoquantas têm três propriedades fundamentais:
X
2
(mil
• são decrescentes da esquerda para a direita;
ho)
• são convexas com relação à origem dos eixos cartesianos; e

11. • não se cruzam e nem se tangenciam.
Uma infinidade de isoquantas no espaço x1 versus x2 denomina-se mapa de isoquantas
4.1. Mapa de Isoproduto
Da mesma forma que as curvas de Indiferença as isoquantas mais elevadas representam
níveis de produção (Y) mais altos e vice-versa.
O nível de produção Y3 é maior que Y2, eY2 é maior que Y1.
X
1
Y
4.2. Taxa Marginal Técnica de Substituição Y
Y
3
Conceito semelhante a TMS na Teoria do Consumidor, isto é, mostra um montante de um
2
1
X
recurso (X1) que o produtor deve liberar para adquirir uma unidade do outro recurso (X 2) a fim de que
a produção permaneça constante.
∆X 1
TMTSx1 x 2 = −
∆X 2 ou
2
TMTSx1 x 2 = −
dX 1
dX 2 (inclinação no ponto considerado).
Como o Produto tem que permanecer constante para qualquer movimento numa
determinada Isoquanta, a contribuição para o produto de uma variação de X1 tem que ser
exatamente compensada pela contribuição de X2 para o produto. Daí, temos:
- ∆X1 PMaX1 = ∆X2 . PMaX2
TMTSX1X2 = -
∆X 1 PMaX 2
=
∆X 2
PMaX 1
ou
TMTSX1X2 =
∆X 1
PMaX 2
=−
∆X 2
PMaX 1
Em qualquer ponto da isoquanta a TMTSX1X2 é dada para inclinação no
ponto considerado .
TMTSX1X2 = -
dX 1
dX 2

12. X
1
A
∆X1
B
∆X 2
X
Obs: A TMTSX1X2 decrescente diz que o empresário está disposto a abrir mão de quantidades cada
2
vez menor do fator X1 por unidades adicionais de X2 .
Exemplo: Se Y= feijão e os fatores de produção são X 1 (mão-de-obra) e X2 (equipamentos). O que
quer dizer uma TMSTx1,x2 = - 3? Significa dizer que: para que o produtor de feijão continue com a
mesma produção deverá retirar três empregados, para a colocação de um equipamento.
4.3. A Região Racional (Econômica) da Produção
Podemos dividir o mapa de Isoquantas em 3 áreas distintas.
X1
•
•
•
TMTSX1X2 = ∞
A
•
•
•
B TMTS
=0
X1X2
0
X2
As linhas OA e OB são chamadas Fronteiras de Produção ou linhas Rigidas ou linhas de
CUME.
A linha OA → é a linha de fronteiras que une os pontos onde as isoquantas tem TMTS X1X2
Infinitas. Elas nos mostra as mínimas quantidades do fator X2 necessárias para produzir diferentes
quantidades do produto.
A linha OB → é a linha de fronteira que une os pontos onde as isoquantas têm TMTS X1X2
nulas. Ela nos mostra as mínimas quantidades do fator X 1 necessárias para produzir diferentes
quantidades do produto.
Conclusão: A área compreendida entre as linhas rigidas é que é a área racional de produção.
4.4. Isocusto
Representa as diferentes combinações de fatores que a firma pode adquirir a um mesmo
custo (com um dado nível de despesa).

13. Seja Y = f(X1, X2)
Onde:
X1 e X2 são os fatores variáveis;
PX1 e PX2 são os preços dos fatores variáveis.
Então,
PX1X1 + PX2X2 = C
Dispêndio maior que
Dispêndio menor que
A Inclinação da Isocusto será:
-
C
PX 1
C
PX 2
=
PX 2
C PX 2
⋅
=−
.
PX 1 C
PX 1
4.5. Combinação de Custo Mínimo (Combinação Ótima dos fatores)
Se o objetivo da firma é maximizar lucro, o problema com que se defronta ao fazer
determinado dispêndio, é o de alcançar a mais alta isoproduto, que sua curva de Isocusto permita,
isto é, obter a máxima quantidade do produto, dado certo dispêndio com os recursos.
X1
C
PX 1
X1’
•1
•2
3
•
X2’
4
••5
C
PX 2
X2

14. Y2 – representa a máxima produção que pode ser obtida com o dispêndio C → pois, qualquer outra
combinação de X1 e X2 sobre a linha de Isocusto, levará a firma para uma isoquanta mais baixa
(veja ponto 2).
Alternativamente a combinação X1’ e X2’ (combinação 3) pode ser conbsiderada como aquela
que produz dada quantidade do produto (Y2 no caso) ao menor custo possível (veja ponto 1 e 2).
No ponto 3, (equilíbrio) temos:
Inclinação do Isoquanta = -
Inclinação da Isocusto = -
∆X 1 dX 1
=
∆X 2 dX 2
como TMTS =
dX 1
PMaX 2
=−
dX 2
PMaX1
PX 2
PX 1
Estas inclinações são iguais no ponto 3:
Logo:
TMTSX1X2 =
dX 1 PMaX 2 PX 2
=
=
dX 2 PMaX 1 PX 1
(no ponto de equilíbrio)
ou
PFMaX 1 PFMaX 2
=
PX 1
PX 2
X
4.6. Caminho de Expansão ou Linha de Escala
1
Existem certas ocasiões que é interessante para a firma aumentar a produção. Para isto ela
deve aumentar o dispêndio com os recursos (X 1 e X2). Porém, qualquer que seja a despesa, a firma
deverá produzir sempre a máxima produção com aquele dispêndio, C alternativamente, produzir
ou
determinada quantidade sempre ao menor custo.
E
Mudança no dispêndio da firma dados os preços de X 1 e X2 deslocarão a curva de Isocusto
paralelamente.
Y
Y4
Y
Y
2
3
C1 1 C 2 C 3
PX 2 PX 2 PX 2
C4
PX 2
X
2

15. Assim, C1 seria o menor custo possível para produzir Y 1, C2 seria o menor custo possível para
produzir Y2, etc.
A linha a b c d chama-se caminho de expansão e mostra o comportamento da firma quando
ela se expande.
LINHA DE EXPANSÃO: é a linha que une os pontos de equilíbrio (combinação de menor custo) para
cada dispêndio possível de firma (quando a firma resolve se expandir).
Mostra o modo mais barato de produzir cada volume de produção, dado os preços dos
fatores.