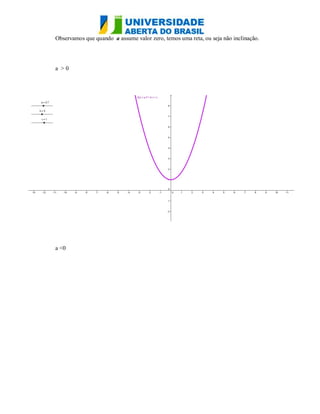
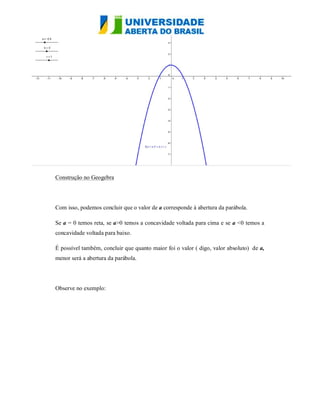
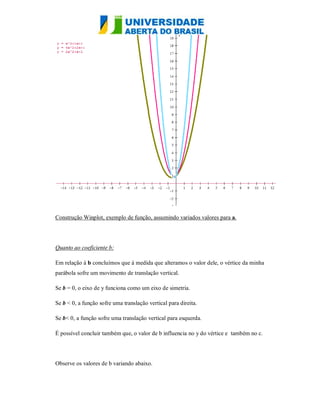
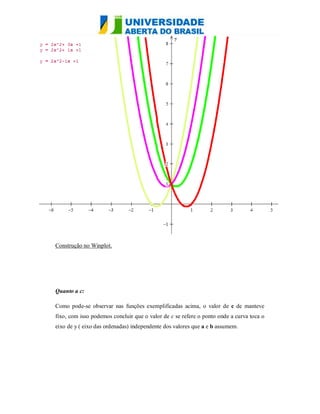
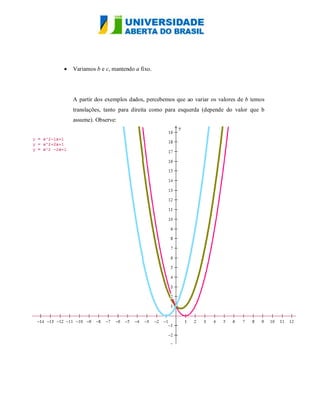
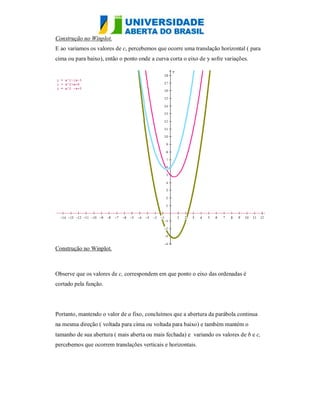
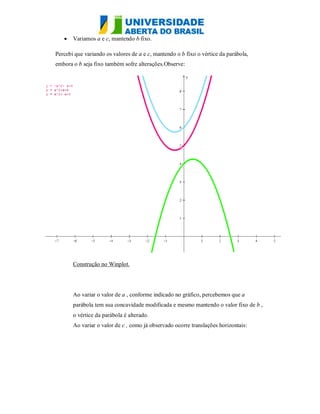
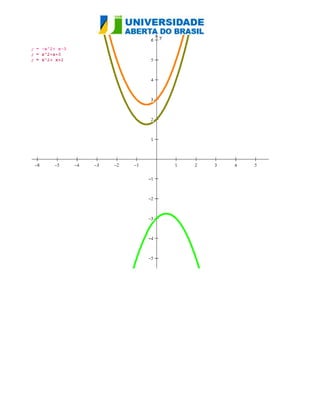
O documento analisa as funções quadráticas f(x) = ax² + bx + c, destacando como a variação dos coeficientes a, b e c afeta o gráfico da parábola. O coeficiente a determina a concavidade e a abertura da parábola, enquanto b provoca translações verticais e influencia a posição do vértice. O coeficiente c define onde a curva intercepta o eixo y, e suas variações causam translações verticais da função.

1. Aluna: Carla Soares Restier Lima Carvalho
Polo: Volta Redonda
Tarefa IV
Em uma função quadrática qualquer, f (x) = ax² + bx + c, diga quais restrições impostas
ao gráficos de f quando:
 Variamos a e b , mantendo c fixo.
Ao variarmos o valor de a e b, mantendo c fixo, observamos os seguintes
comportamentos:
Quanto ao coeficiente a:
a=0
Gráfico desenvolvido no Geogebra, utilizando a ferramenta “seletor” com o objetivo de
manipular o gráfico, variando as constante a e b, sem necessidade de traçar outros
gráficos.

2. Observamos que quando a assume valor zero, temos uma reta, ou seja não inclinação.
a >0
a <0

3. Construção no Geogebra
Com isso, podemos concluir que o valor de a corresponde à abertura da parábola.
Se a = 0 temos reta, se a>0 temos a concavidade voltada para cima e se a <0 temos a
concavidade voltada para baixo.
É possível também, concluir que quanto maior foi o valor ( digo, valor absoluto) de a,
menor será a abertura da parábola.
Observe no exemplo:

4. Construção Winplot, exemplo de função, assumindo variados valores para a.
Quanto ao coeficiente b:
Em relação à b concluímos que à medida que alteramos o valor dele, o vértice da minha
parábola sofre um movimento de translação vertical.
Se b = 0, o eixo de y funciona como um eixo de simetria.
Se b < 0, a função sofre uma translação vertical para direita.
Se b< 0, a função sofre uma translação vertical para esquerda.
É possível concluir também que, o valor de b influencia no y do vértice e também no c.
Observe os valores de b variando abaixo.

5. Construção no Winplot.
Quanto a c:
Como pode-se observar nas funções exemplificadas acima, o valor de c de manteve
fixo, com isso podemos concluir que o valor de c se refere o ponto onde a curva toca o
eixo de y ( eixo das ordenadas) independente dos valores que a e b assumem.

6.  Variamos b e c, mantendo a fixo.
A partir dos exemplos dados, percebemos que ao variar os valores de b temos
translações, tanto para direita como para esquerda (depende do valor que b
assume). Observe:

7. Construção no Winplot.
E ao variamos os valores de c, percebemos que ocorre uma translação horizontal ( para
cima ou para baixo), então o ponto onde a curva corta o eixo de y sofre variações.
Construção no Winplot.
Observe que os valores de c, correspondem em que ponto o eixo das ordenadas é
cortado pela função.
Portanto, mantendo o valor de a fixo, concluímos que a abertura da parábola continua
na mesma direção ( voltada para cima ou voltada para baixo) e também mantém o
tamanho de sua abertura ( mais aberta ou mais fechada) e variando os valores de b e c,
percebemos que ocorrem translações verticais e horizontais.

8.  Variamos a e c, mantendo b fixo.
Percebi que variando os valores de a e c, mantendo o b fixo o vértice da parábola,
embora o b seja fixo também sofre alterações.Observe:
Construção no Winplot.
Ao variar o valor de a , conforme indicado no gráfico, percebemos que a
parábola tem sua concavidade modificada e mesmo mantendo o valor fixo de b ,
o vértice da parábola é alterado.
Ao variar o valor de c , como já observado ocorre translações horizontais: