(1) O documento apresenta dois exercícios resolvidos e quatro propostos sobre a equação da continuidade aplicada a escoamentos de fluidos. (2) Os exercícios tratam de problemas de escoamento permanente em tubulações e caixas com entradas e saídas de diferentes seções. (3) São solicitados cálculos de velocidades nos diferentes pontos dos sistemas usando a equação da continuidade.

1. 3ª Lista de Exercícios
Conservação de Massa – Equação da Continuidade
EXERCÍCIOS RESOLVIDOS
(1) Considere o movimento permanente da água (ρ = 999,8 Kg/m3
) através do
volume conforme figura.
y
(4)
60º x
(1) (3)
30º
(2)
• As seções de cada entrada ou saída possuem as seguintes áreas:
A1 = 0,0186 m2
A2 = 0,0464 m2
A3 = A4 = 0,0371 m2
• A massa fluida que sai pela seção (3) é igual a 56,648 Kg/s.
• O volume que entra pela seção (4) é de 0,0283 m3
/s.
• A velocidade em (1) é V1 = 3,048. î (m/s)
Admitindo que as propriedades do fluido sejam uniformes em todas as seções,
determinar a velocidade do escoamento na seção (2).
Solução:
1

2. - Em primeiro lugar definir o volume de controle (VC)
(4)
VC
60º
(1) (3)
30º
(2)
- Equação básica:
∂ → →
 ρ. dVol + ρ. V . dA = 0
∂t VC SC
Para movimento permanente, por definição, temos que o primeiro termo da equação
básica é nulo, portanto:
→ →
ρ. V . dA = 0
SC
Assim,
→ → → → → → → → → →
ρ. V . dA = ρ. V. dA + ρ. V. dA + ρ. V. dA + ρ. V . dA = 0
SC A1 A2 A3 A4
Logo,
→ → → → → → → →
ρ. V. dA = − ρ. V. dA − ρ. V. dA − ρ. V . dA
A2 A1 A3 A4
2

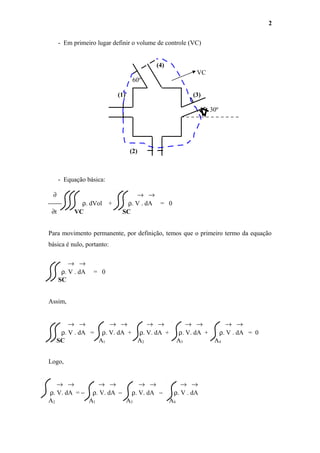
3. Verificar cada uma das seções:
• Seção (1):
→ →
ρ . V . dA = −ρ . V1 . A1
A1
• Seção (3):
→ → •
ρ . V . dA = ρ . V3 . A3 = m3
A3
• Seção (4):
→ →
ρ . V . dA = −ρ . V4 . A4 = − ρ.Q4
A4
Assim, para a seção (2):
→ → •
ρ. V. dA = ρ . V1 . A1 − m3 + ρ.Q4
A2
→ →
ρ. V. dA = [999,84 × 3,048 × 0,0186 ] − 56,648 + [999,84 × 0,0283] = 28,331 Kg/s
A2
Portanto, em (2) sai um fluxo de 28,331 Kg/s (positivo)
→ →
Logo: ρ . V . dA = ρ . V2 . A2
A2
ρ . V2 . A2= 28,331 Kg/s
V2 = [28,331 / 999,84 × 0,0464] = 0,61 m/s
Como V2 é negativo em relação ao eixo (y) temos:
3

4. V2 = − 0,61. ĵ (m/s)
(2) Um recipiente de volume 0,05 m3
, contem ar a 800 Kpa (absoluto) e a 15º C. Ao
tempo (t = 0), o ar começa a escapar deste recipiente através da válvula, com área
igual a 65 mm2
. Ao passar pela válvula, o ar tem velocidade de 311 m/s e massa
especifica de 6,13 Kg/m3
. Em cada instante, as propriedades do ar no resto do tanque
são consideradas constantes. Determinar a taxa de variação da massa especifica do ar
no recipiente no instante (t = 0).
Dados:
• Volume do recipiente = 0,05 m3
• Ar = pressão 800 KPa, T = 15ºC, no (t = 0)
• Velocidade = 311 m/s
• ρ = 6,13 Kg/m3
• Área da válvula = 65 mm2
VC y
(1) SC
x
Solução:
- Equação básica:
∂ → →
 ρ. dVol + ρ. V . dA = 0
∂t VC SC
Como as propriedades no tanque foram consideradas constantes em qualquer instante
temos:
∂ → →
 [ ρVC dVol ] + ρ. V . dA = 0
∂t VC SC
(1)
4

5. ∂ → → V
 [ ρVC . Vol ] + ρ. V . dA = 0 sinal (+)
∂t VC A1 A1
∂
 [ ρVC . Vol ] +  ρ1. V1 . A1  = 0
∂t
∂
 [ ρVC . Vol ] = − ρ1. V1 . A1
∂t
Como o volume (Vol) não é função do tempo, a expressão acima fica:
∂ ρVC
[ Vol ]  = − ρ1. V1 . A1
∂t
∂ ρVC − ρ1. V1 . A1
 = 
∂t Vol
Portanto no instante (t = 0):
∂ ρVC − 6,13 × 311 × 65.10−6
 =  = − 2,48 Kg/m3
/s
∂t 0,05
5

6. EXERCÍCIOS PROPOSTOS
(1) Considere o escoamento de um fluido incompressível em regime permanente,
interno a uma tubulação, atravessando um acessório convergente para ligar um tubo
de maior diâmetro a um tubo de menor diâmetro, conforme figura. Utilize a equação
da continuidade para caracterizar a velocidade em cada região do escoamento. Fazer
as hipóteses que julgar necessário.
A1 A2
(1) (2)
(3)
D1 V1 V2 D2
Resposta: V1 . A1 = V2 . A2
(2) Na junção de duas tubulações, conforme figura, são misturados dois fluidos. Na
tubulação (1) escoa um fluido com massa especifica (ρ1) e vazão (Q1). Na tubulação
(2) escoa um fluido com massa especifica (ρ2) e vazão (Q2). Sabendo que a vazão na
tubulação (3) é (Q3). Calcular a massa especifica (ρ3) da mistura.
(1)
(3)
(2) VC
(ρ1) × (Q1) + (ρ2) × (Q2)
Resposta: (ρ3) = 
(Q3)
(3) A massa especifica de um fluido é (ρ = 1.050 Kg/m3
). Este fluido escoa em
movimento permanente através de uma caixa de seção retangular conforme figura.
Pede-se V3 . V2
(2)
(y)
6
VC

7. → (1) (3) (x)
V1
Dados:
- A1 = 0,05 m2 e V1 = 4.î (m/s)
- A2 = 0,01m2 e V2 = - 8.ĵ (m/s)
- A3 = 0,06 m2 e V3 = ?
Resposta: V3 = (4,04.î − 2,34.ĵ) m/s
(4) Um fluido em contato com o contorno de um corpo sólido estacionário tem
velocidade nula. Não há deslizamento neste contorno. O escoamento sobre aplaca
plana adere à superfície e forma a camada limite conforme figura. O escoamento
antes da placa é uniforme com velocidade (V = U.î), sendo (U = 30 m/s). A
distribuição das velocidades no interior da camada limite (0 ≤ y ≤ δ) na seção “c.d”
é aproximadamente, u = 2.U.[(y/δ) − (y/δ)2
] .
A espessura da camada limite nesta seção é de (5 mm).
O fluido é o ar com massa especifica (ρ = 1,24 Kg/m3
).
Admitindo se (0,60 m) a largura da placa, pede-se calcular o escoamento de massa
através da superfície no traço “b.c” do volume de controle que se projeta “ a.b.c.d ”.
y
x
U Fronteira da
(b) (c) camada limite
δ = 5 mm
(a) (d)
Dados:
- ρ = 1,24 Kg/m3
- Largura da placa w = 0,60 m
- A velocidade na placa é uniforme V = U.î, sendo U = 30 m/s.
- Em “c.d”:
δ = 5 mm
u = 2.U.[(y/δ) − (y/δ)2
]
Determinar o escoamento de massa fluida através da superfície de traço “b.c”.
7
VC

8. .
Resposta : mbc = ∫∫ ρ . V . dA = 0,0372 Kg/s
Abc
8