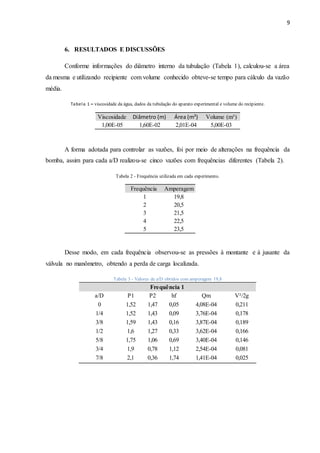
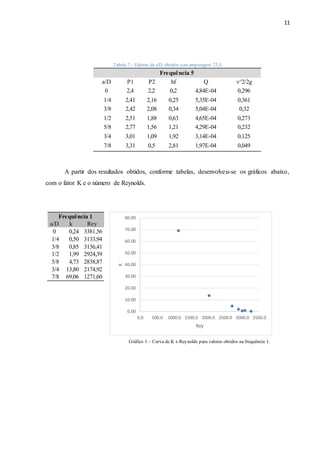
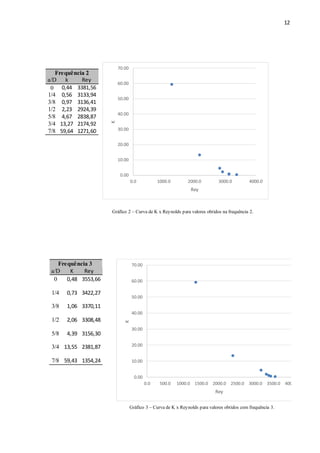
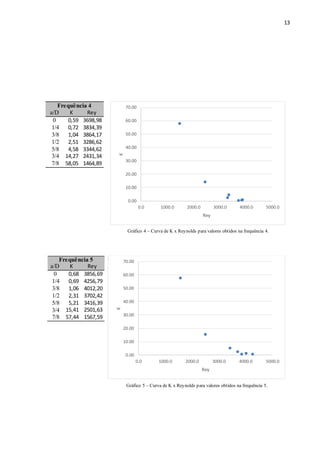
O documento aborda a análise das perdas de carga localizadas em condutos forçados, com foco na influência da válvula de gaveta. O estudo foi realizado por meio de experimentos com tubos de PVC e medições de pressão, buscando comparar os resultados encontrados com dados tabelados na literatura. Os principais objetivos incluem avaliar as variações de vazão e o efeito do fechamento da válvula nas perdas de carga, utilizando métodos de cálculo específicos.

1. 1
UNIVERSIDADE FEDERAL DE MATO GROSSO
FACULDADE DE ARQUITETURA, ENGENHARIA E TECNOLOGIA
DEPARTAMENTO DE ENGENHARIA SANITÁRIA E AMBIENTAL
HIDRÁULICA EM CONDUTOS FORÇADOS
PERDAS DE CARGA LOCALIZADAS
Igor Pinto London
Julyane Souza Cruz
Lucas Olegário Bueno
Maria Eduarda Curvo Jaudy
CUIABÁ – MT
JUNHO/2017

2. 2
UNIVERSIDADE FEDERAL DE MATO GROSSO
FACULDADE DE ARQUITETURA, ENGENHARIA E TECNOLOGIA
DEPARTAMENTO DE ENGENHARIA SANITÁRIA E AMBIENTAL
HIDRÁULICA EM CONDUTOS FORÇADOS
PERDAS DE CARGA LOCALIZADAS
Relatório apresentado à disciplina de
Hidráulica de Condutos Forçados do curso de
Engenharia Sanitária e Ambiental da
Universidade Federal de Mato Grosso, como
requisito parcial de avaliação.
Prof. Dr. Wellintom Ttatom Pereira da Silva
CUIABÁ – MT
JUNHO/2017

3. 3
SUMÁRIO
1. Introdução .....................................................................................................................4
2. Modelo Conceitual.........................................................................................................5
3. Objetivo .........................................................................................................................5
4. Aparato Experimental..................................................................................................6
5. Materiais e Métodos......................................................................................................7
5.1. Materiais.........................................................................................................................7
5.2. Procedimentos................................................................................................................7
6 Resultados e Discussões.................................................................................................7
7. Conclusões ..................................................................................................................12
8. Referências Bibliográficas...........................................................................................13

4. 4
1. INTRODUÇÃO
O estudo do comportamento hidráulico de fluidos em condutos forçados é importante
devido ao conhecimento que se obtém referente à pressão com a qual o mesmo sairá de alguma
estação e com as perdas que ele sofrerá durante seu percurso, tanto as perdas distribuídas quanto
as localizadas, mas nesse experimento foram objeto de estudo durante o procedimento
laboratorial apenas as perdas de cargas localizada.
As instalações de transporte de água sob pressão, de qualquer porte, são constituídas por
tubulações montadas em sequências, de eixo retilíneo, unidas por acessórios de diversas
natureza, os quais causam variações bruscas, devido a geometria dos escoamentos, como
mudanças de direção ou da seção do fluxo com válvula, curvas, derivações, registros ou
conexões de qualquer tipo e uma máquina hidráulica com bomba (PORTO, 2006)
Em virtude da presença dos acessórios necessários para a operação do sistema, ocorre a
alteração de módulo ou direção da velocidade média e consequentemente de pressão localizada.
Desse modo, isto se reflete em um acréscimo de turbulência que produz perdas de carga que
deverá ser agregada às perdas distribuídas, devido ao atrito, ao longo dos trechos retilíneos das
tubulações, a essas perdas denomina-se como perdas de carga localizada ou singulares
(PORTO, 2006).
A perda de carga localizada pode ser estimada por três métodos: Expressão de Borda-
Belanger (fator K), comprimento equivalente e diâmetro equivalente. Existem várias tabelas
que permitem determinar a perda de carga localizada por esses métodos para fluidos
newtonianos (SAMPAIO, 2010).
Perdas de carga em válvulas de gaveta, a qual será desenvolvida neste experimento,
podem oferecer uma grande resistência ao escoamento. Mesmo quando totalmente aberto,
haverá uma perda de carga sensível devido à sua própria construção (NETTO, 1998).

5. 5
2. MODELO CONCEITUAL
Para que fosse notada a diferença, durante o desenvolvimento do estudo, as
características hidráulicas no fluido em consequência da parcela de abertura da válvula, a
equação 1 foi analisada a fim de que ao final se descobrisse o K, cujo qual apresenta os valores
do coeficiente K em função do grau de fechamento da válvula.
∆𝐻 = 𝑘
𝑣2
2𝑔
(𝑚) (1)
Onde:
∆H = perda de carga localizada, causada pela válvula de gaveta
𝑘 = coeficiente adimensional
𝑣2
2𝑔
= velocidade cinética
O fator (K) depende da geometria da conexão, do número de Reynolds (𝑅 𝑒 ), da
rugosidade (Ɛ) da parede e, em alguns casos da velocidade do escoamento. A velocidade (V) é
uma velocidade média de referência, em geral nas peças em que há mudança de diâmetro,
tomada como a velocidade média na seção de menor diâmetro (PORTO, 2006).
Figura 1 - Perda de carga localizada em válvula de gaveta (PORTO, 2006).
Durante o procedimento as marcações de abertura foram realizadas justamente para que
se tivesse conhecimento do quão aberto estava a válvula, para que posteriormente pudesse ser
comparada com a literatura.

6. 6
3. OBJETIVOS
O presente trabalho tem por objetivo analisar as perdas de cargas localizadas, em um
tubo de PVC, verificando a influência da vazão, diâmetro do tubo e do registro de gaveta,
comparando os resultados obtidos através das observações com valores tabelados. Assim,
verificar a perda de caga localizada ao longo do fechamento da gaveta.
4. APARATO EXPERIMENTAL
Figura 2 - Esquema do aparato simplificado de corpo de prova. Fonte: Autor
O aparato experimental para realização do trabalho, consistiu nos seguintes
componentes:
A. Reservatório contendo água
B. Bomba
C. Válvula de Gaveta
1. Manômetro de Entrada
2. Manômetro de Saída
A figura 2 apresenta um sistema simplificado de corpo de prova, em escala de
laboratório, onde foi realizado os estudos acerca das perdas de cargas localizadas com

7. 7
escoamento turbulento, por meio da observação das pressões nos manômetros e controle da
vazão pela válvula de gaveta.
Considerou-se o tubo PVC roscável de ½” (0,016 m) de diâmetro interno, vazão e fator
de atrito.
O corpo de prova é composto por duas perfurações no cano com engates rápidos para
acoplar os manômetros e duas válvulas para controle do fluxo de água.
Entre o manômetro 1 ao 2 encontra-se a válvula de gaveta.
5. MATERIAIS E MÉTODOS
5.1 Materiais
Utilizou-se, além do aparato experimental supracitados anteriormente, relógio
cronômetro e recipiente com marcação e volume de 5L para cálculo de tempo e vazão.
O acessório implementado como objeto de estudo da perda de carga localizada foi o
Registro de Gaveta, ou Válvula de Gaveta, que permite regular a vazão transportada e até
mesmo promover o fechamento total. Além disso, foi utilizado um regulador de frequência,
para controlar a vazão.
Com os dados coletados e tabelados em Microsoft Excel 2013, calculou-se o fator de
atrito e o número de Reynolds.
5.2 Procedimento Experimental
O experimento em laboratório consistiu no seguinte procedimento:
a) Instalou-se o corpo de prova junto a saída de água do sistema e instalou-se os
manômetros. A bomba foi acionada, juntamente com os registros e foi aguardada a
estabilização do sistema.
b) Ajustou-se a vazão com o auxílio da frequência da bomba;
c) Iniciou-se as tomadas de pressão a montante e jusante do registro de gaveta e seus
respectivos tempos, em triplicatas, necessários para encher um recipiente com
volume de 5 litros.
Partindo-se do princípio de que a válvula de menores proporções, na qual era pretendida
analisar a perda de carga, era aberta regularmente para que mantivesse o padrão já
preestabelecido na tabela que contém os coeficientes de K.

8. 8
Elaborou-se uma planilha de cálculos utilizando a ferramenta MS Excel, calculou-se:
a) Vazão média;
b) Velocidade;
c) Perda de carga em mmg e m.c.a;
d) Coeficiente K
Os valores obtidos auxiliaram ao para projetar a tabela K x a/D, possibilitando assim a
comparação de seu comportamento com o esperado, baseado na literatura.
Quando totalmente abertas, essas válvulas não produzem efeito significativo no
escoamento, porém, quando altera-se a relação de diâmetro neste ponto, por meio do
fechamento deste registro, provocam perdas de cargas localizada consideráveis.
Como objeto de estudo, seu processo de fechamento se dá através de uma lâmina
vertical, mostrado na Figura 3, que diminui a passagem do fluido pela tubulação, alterando a
vazão deste.
Figura 3: Registro aberto e Registro fechado
Fonte:(NETTO, MANUAL DE HIDRÁULICA, 1998)

9. 9
6. RESULTADOS E DISCUSSÕES
Conforme informações do diâmetro interno da tubulação (Tabela 1), calculou-se a área
da mesma e utilizando recipiente com volume conhecido obteve-se tempo para cálculo da vazão
média.
Tabela 1 – viscosidade da água, dados da tubulação do aparato experimental e volume do recipiente.
Viscosidade Diâmetro (m) Área (m²) Volume (m³)
1,00E-05 1,60E-02 2,01E-04 5,00E-03
A forma adotada para controlar as vazões, foi por meio de alterações na frequência da
bomba, assim para cada a/D realizou-se cinco vazões com frequências diferentes (Tabela 2).
Tabela 2 - Frequência utilizada em cada experimento.
Frequência Amperagem
1 19,8
2 20,5
3 21,5
4 22,5
5 23,5
Desse modo, em cada frequência observou-se as pressões à montante e à jusante da
válvula no manômetro, obtendo a perda de carga localizada.
Tabela 3 - Valores de a/D obtidos com amperagem 19,8
Frequência 1
a/D P1 P2 hf Qm V²/2g
0 1,52 1,47 0,05 4,08E-04 0,211
1/4 1,52 1,43 0,09 3,76E-04 0,178
3/8 1,59 1,43 0,16 3,87E-04 0,189
1/2 1,6 1,27 0,33 3,62E-04 0,166
5/8 1,75 1,06 0,69 3,40E-04 0,146
3/4 1,9 0,78 1,12 2,54E-04 0,081
7/8 2,1 0,36 1,74 1,41E-04 0,025

10. 10
Tabela 4 - Valores a/D obtidos com amperagem 20,5.
Frequência 2
a/D P1 P2 hf Q V²/2g
0 1,69 1,59 0,1 4,25E-04 0,228
1/4 1,68 1,57 0,11 3,94E-04 0,196
3/8 1,72 1,53 0,19 3,94E-04 0,196
1/2 1,77 1,39 0,38 3,67E-04 0,17
5/8 1,91 1,16 0,75 3,57E-04 0,16
3/4 2,09 0,84 1,25 2,73E-04 0,094
7/8 2,3 0,38 1,92 1,60E-04 0,032
Tabela 5 - Valores de a/D obtidos com amperagem 21,5.
Frequência 3
a/D P1 P2 hf Q v^2/2g
0 1,92 1,8 0,12 4,46E-04 0,251
1/4 1,93 1,76 0,17 4,30E-04 0,233
3/8 1,92 1,68 0,24 4,23E-04 0,226
1/2 2 1,55 0,45 4,16E-04 0,218
5/8 2,16 1,29 0,87 3,97E-04 0,198
3/4 2,36 0,83 1,53 2,99E-04 0,113
7/8 2,59 0,42 2,17 1,70E-04 0,037
Tabela 6 - Valores de a/D obtidos com amperagem 22,5
Frequência 4
a/D P1 P2 hf Q v^2/2g
0 2,14 1,98 0,16 4,65E-04 0,272
1/4 2,16 1,95 0,21 4,82E-04 0,293
3/8 2,17 1,86 0,31 4,85E-04 0,297
1/2 2,26 1,72 0,54 4,13E-04 0,215
5/8 2,43 1,41 1,02 4,20E-04 0,223
3/4 2,67 0,99 1,68 3,05E-04 0,118
7/8 2,94 0,46 2,48 1,84E-04 0,043

11. 11
Tabela 7 - Valores de a/D obtidos com amperagem 23,5.
Frequência 5
a/D P1 P2 hf Q v^2/2g
0 2,4 2,2 0,2 4,84E-04 0,296
1/4 2,41 2,16 0,25 5,35E-04 0,361
3/8 2,42 2,08 0,34 5,04E-04 0,32
1/2 2,51 1,88 0,63 4,65E-04 0,273
5/8 2,77 1,56 1,21 4,29E-04 0,232
3/4 3,01 1,09 1,92 3,14E-04 0,125
7/8 3,31 0,5 2,81 1,97E-04 0,049
A partir dos resultados obtidos, conforme tabelas, desenvolveu-se os gráficos abaixo,
com o fator K e o número de Reynolds.
Frequência 1
a/D k Rey
0 0,24 3381,56
1/4 0,50 3133,94
3/8 0,85 3136,41
1/2 1,99 2924,39
5/8 4,73 2838,87
3/4 13,80 2174,92
7/8 69,06 1271,60
Gráfico 1 – Curva de K x Reynolds para valores obtidos na frequência 1.
0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
80.00
0.0 500.0 1000.0 1500.0 2000.0 2500.0 3000.0 3500.0
K
Rey

12. 12
Gráfico 2 – Curva de K x Reynolds para valores obtidos na frequência 2.
0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
0.0 1000.0 2000.0 3000.0 4000.0
K
Rey
Frequência 2
a/D k Rey
0 0,44 3381,56
1/4 0,56 3133,94
3/8 0,97 3136,41
1/2 2,23 2924,39
5/8 4,67 2838,87
3/4 13,27 2174,92
7/8 59,64 1271,60
Frequência 3
a/D K Rey
0 0,48 3553,66
1/4 0,73 3422,27
3/8 1,06 3370,11
1/2 2,06 3308,48
5/8 4,39 3156,30
3/4 13,55 2381,87
7/8 59,43 1354,24
Gráfico 3 – Curva de K x Reynolds para valores obtidos com frequência 3.
0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
0.0 500.0 1000.0 1500.0 2000.0 2500.0 3000.0 3500.0 4000.0
K
Rey

13. 13
Frequência 4
a/D K Rey
0 0,59 3698,98
1/4 0,72 3834,39
3/8 1,04 3864,17
1/2 2,51 3286,62
5/8 4,58 3344,62
3/4 14,27 2431,34
7/8 58,05 1464,89
Gráfico 4 – Curva de K x Reynolds para valores obtidos na frequência 4.
0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
0.0 1000.0 2000.0 3000.0 4000.0 5000.0
K
Rey
Frequência 5
a/D K Rey
0 0,68 3856,69
1/4 0,69 4256,79
3/8 1,06 4012,20
1/2 2,31 3702,42
5/8 5,21 3416,39
3/4 15,41 2501,63
7/8 57,44 1567,59
Gráfico 5 – Curva de K x Reynolds para valores obtidos na frequência 5.
0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
0.0 1000.0 2000.0 3000.0 4000.0 5000.0
K
Rey

14. 14
7. CONCLUSÃO
Em tubulações onde ser trabalha com sistemas de abastecimentos, ou seja, que utiliza
condutos forçados, existirá sempre trechos com diâmetros diferentes e diversos acessórios, e
portanto, estará sempre sujeitos a perda de carga durante todo o percurso do fluido, desde perda
de carga distribuída e perda de carga localizada
Analisando os resultados obtidos através do experimento, nota-se escoamento
turbulento, com valores de Reynolds calculados entre 2 mil e 40 mil. Devido às limitações
laboratoriais, não foi possível obter valores de Reynolds entre 20.000 e 120.000, em virtude do
diâmetro do tubo utilizado ser pequeno, assim as frequências utilizadas foram relativamente
baixas.
Concluiu-se que quanto maior o coeficiente K da parede do tubo menor é o número de
Reynolds. Evidenciando que o valor do coeficiente de perda de carga aumenta conforme o
fechamento da válvula, havendo queda de energia.
.

15. 15
Bibliografia
NETTO, A. (1998). MANUAL DE HIDRÁULICA. SÃO PAULO: ACÁCIO EIJI ITO - 8ª
EDIÇÃO.
PORTO, R. D. (2006). HIDRÁULICA BÁSICA. SÃO CARLOS, SP: Escola de Engenharia de
São Carlos, Universidade de São Paulo, 4 Ed., 2006, .
SAMPAIO, S. (2010). PERDA DE CARGA DISTRIBUÍDA E LOCALIZADA EM
TUBULAÇÕES. p. 15.
.