1) O documento discute os conceitos básicos de eletrostática e eletrodinâmica, incluindo carga elétrica, eletrização, condutores e isolantes.
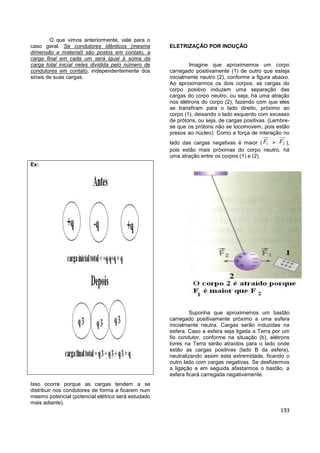
2) Existem dois tipos de carga elétrica: positiva e negativa. Cargas do mesmo sinal se repelem e cargas de sinais opostos se atraem.
3) A carga elétrica de um corpo é medida pelo número de elétrons ou prótons em excesso, e pode ser positiva, negativa ou neutra.