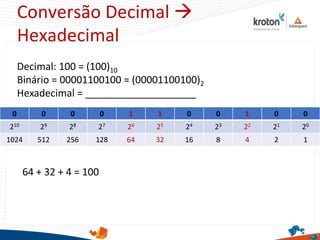
1) O documento discute sistemas de numeração como binário, decimal, octal e hexadecimal. Mostra como converter entre esses sistemas de numeração. 2) Apresenta o sistema BCD (Binary Coded Decimal) que representa cada dígito decimal com 4 bits binários de acordo com o sistema ponderado 8, 4, 2, 1. 3) Explica que números binários entre 0000 e 1001 são válidos em BCD, enquanto números entre 1010 e 1111 são inválidos porque não representam um único dígito decimal.

1. SISTEMAS DIGITAIS
Aula 4: Unidade 1 Seção 2
Prof.ª M.ª Eng.ª Elaine Cecília Gatto
Material Extra
1

2. Sistemas de Numeração
•LSB = Least Signifcant Bit ou Bit Menos Significativo
•MSB = Most Significant Bit ou Bit Mais Significativo
•Até onde você pode contar usando um número de x
bits?
• X = 5  2x – 1 = 25 – 1 = 32 – 1 = 3
•Quantos nímeros podem ser representados com x
bits?
• X = 1  2x = 21 = 2 combinaçoões
• X = 10  2x = 210 = 1.024 combinações

3. Binário: 00001110001 = (00001110001)2
Decimal: ___________
Colocar o número binário na tabela
Obs.: este número binário tem 11 BITS.
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
Conversão Binário  Decimal

4. Conversão Binário  Decimal
Binário: 00001110001 = (00001110001)2
Decimal: ___________
Agora somar os números onde o número
1 aparece:
0 0 0 0 1 1 1 0 0 0 1
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1

5. Conversão Binário  Decimal
Binário: 00001110001 = (00001110001)2
Decimal: ___________
0 0 0 0 1 1 1 0 0 0 1
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
64 + 32 + 16 + 1 = 113

6. Conversão Binário  Decimal
Binário: 00001110001 = (00001110001)2
Decimal: 113 = (113)10
0 0 0 0 1 1 1 0 0 0 1
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1

7. Conversão Decimal  Binário
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
Decimal: 234 = (234)10
Binário: _________________

8. Conversão Decimal  Binário
1 1
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
Decimal: 234 = (234)10
Binário: _________________
Colocar o número 1 nas posições onde der para somar. Verificar na tabela, onde o
número se encaixa. 256 é maior que 234, portanto, não podemos colocar o
número 1 em 256. Entretanto, 128 + 64 = 192, que é menor que 234, então,
colocamos 1 em 128 e em 64. O processo se repete até conseguir completar o
número. Onde não der para somar, colocamos zero.

9. Conversão Decimal  Binário
0 0 0 1 1 1 0 1 0 1 0
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
Decimal: 234 = (234)10
Binário: 00011101010 = (00011101010)2
128 + 64 + 32 + 8 + 2 = 234

10. Conversão Octal  Decimal
Octal: 627 = (627)8
Decimal: _______
6 2 7
86 85 84 83 82 81 80
262144 32768 4096 512 64 8 1
Para converter um número octal para decimal, basta colocar os números octais
em sequencia na tabela, como mostrado acima. Em seguida, deve ser feito o
seguinte calculo:
(6 * 82) + (2 * 81) + (7 * 80) =
(6 * 64) + (2 * 8) + (7 * 1) =
384 + 16 + 7 =
407

11. Conversão Octal  Decimal
Octal: 627 = (627)8
Decimal: 407 = (407)10
6 2 7
86 85 84 83 82 81 80
262144 32768 4096 512 64 8 1

12. Conversão Decimal  Octal
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
Decimal: 55 = (55)10
Octal: __________
1º Passo: Transformar o número decimal em
número binário

13. Conversão Decimal  Octal
0 0 0 0 0 1 1 0 1 1 1
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
Decimal: 55 = (55)10
Binário: 00000110111 = (00000110111)2
32 + 16 + 4 + 2 + 1 = 55

14. Conversão Decimal  Octal
0 0 0 0 0 1 1 0 1 1 1
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
Decimal: 55 = (55)10
Binário: 00000110111 = (00000110111)2
32 + 16 + 4 + 2 + 1 = 55
2º Passo: Separar os números binários em grupos de 3, começando da direita:
00 | 000 | 110 | 111
Agora completar outra tabela, conforme slide a seguir

15. Conversão Decimal  Octal
4º bit 3º bit do número octal 2º bit do número octal 1º bit do número octal
0 0 0 0 0 1 1 0 1 1 1
21 20 22 21 20 22 21 20 22 21 20
2 1 4 2 1 4 2 1 4 2 1
0 0 4 + 2 = 5 4 + 2 + 1 = 7
Decimal: 55 = (55)10
Binário: 00000110111 = (00000110111)2
Octal: _____________________
Agora, somar as posições que contem os números um,
separadamente, conforme mostra a tabela. O número octal será:
0057

16. Conversão Decimal  Octal
4º bit 3º bit do número octal 2º bit do número octal 1º bit do número octal
0 0 0 0 0 1 1 0 1 1 1
21 20 22 21 20 22 21 20 22 21 20
2 1 4 2 1 4 2 1 4 2 1
0 0 5 7
Decimal: 55 = (55)10
Binário: 00000110111 = (00000110111)2
Octal: 0057 = (0057)8

17. Conversão Hexadecimal 
Decimal
Hexadecimal: CF80 = (CF80)16
Decimal: _______
C F 8 0
165 164 163 162 161 160
12 15 8 0
1048576 65536 4096 256 16 1
Para converter um número hexadecimal para decimal, basta colocar
os números hexadecimais em sequencia na tabela, como mostrado
acima. Em seguida, devemos substituir as letras pelos valores
correspondentes. Somente depois, será feito o cálculo, da mesma
forma que os octais
A 10
B 11
C 12
D 13
E 14
F 15

18. Conversão Hexadecimal 
Decimal
Hexadecimal: CF80 = (CF80)16
Decimal: _______
C F 8 0
165 164 163 162 161 160
12 15 8 0
1048576 65536 4096 256 16 1
A 10
B 11
C 12
D 13
E 14
F 15
(12 * 163) + (15 * 162) + (8 * 161) + ( 0 * 160) =
(12 * 4096) + (15 * 256) + (8 * 16) + (0 * 1) =
49152 + 3840 + 128 + 0 =
53120

19. Conversão Hexadecimal 
Decimal
Hexadecimal: CF80 = (CF80)16
Decimal: 53120 = (53120)10
C F 8 0
165 164 163 162 161 160
12 15 8 0
1048576 65536 4096 256 16 1
A 10
B 11
C 12
D 13
E 14
F 15

20. Conversão Decimal 
Hexadecimal
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
Decimal: 100 = (100)10
Hexadecimal = ____________________
1º Passo: Transformar o número decimal em número binário

21. Conversão Decimal 
Hexadecimal
0 0 0 0 1 1 0 0 1 0 0
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1
64 + 32 + 4 = 100
Decimal: 100 = (100)10
Binário = 00001100100 = (00001100100)2
Hexadecimal = ____________________

22. Conversão Decimal 
Hexadecimal
2º Passo: Separar os números binários em grupos de 4, começando da direita:
000 | 0110 | 0100
Agora completar outra tabela, conforme slide a seguir
Decimal: 100 = (100)10
Binário = 00001100100 = (00001100100)2
Hexadecimal = ____________________
0 0 0 0 1 1 0 0 1 0 0
210 29 28 27 26 25 24 23 22 21 20
1024 512 256 128 64 32 16 8 4 2 1

23. BCD
• Cada dígito é representado com 4 bits binários, de acordo com o sistema
ponderado 8, 4, 2, 1.
• Para converter números decimais para BCD basta dividir o número em grupos de
quatro, cada grupo de 4 bit é correspondente a um número decimal.
• Exemplo: converta o número decimal 3906 para BCD
• Resposta: (3906)10 = (0011100100000110)2
3 9 0 6
0011 1001 0000 0110

24. BCD
• 4 bits = 1 a 15
• Os seis números acima de 9 não são números BCD
válidos, pois não se convertem em um único
número decimal
• Números binários BCD válidos: 0000, 0001, 0010,
0011, 0100, 0101, 0110, 0111, 1000, 1001
• Números binários BCD inválidos: 1010, 1011,
1100, 1101, 1110, 1111.

25. BCD
0110 1001 0011
6 9 3
Convertendo número binário em
número decimal: