[1] O documento apresenta um problema geométrico envolvendo a divisão de um retângulo ABCD em dois polígonos: um quadrado AEFD e um retângulo EBCF semelhante ao retângulo original.
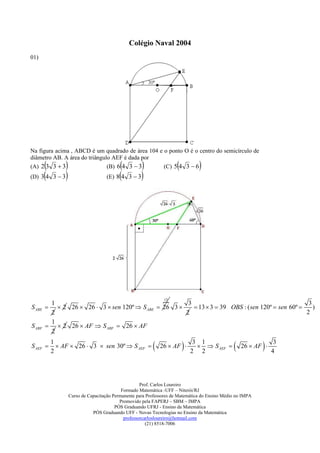
[2] É dada a informação de que os lados do retângulo original são AB = a e BC = b, sendo a > b.
[3] O problema não fornece mais detalhes, mas parece requerer a análise da divisão do retângulo e a caracterização geométrica dos dois polígonos formados.