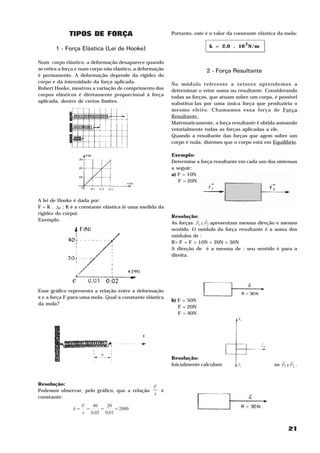
O documento discute diferentes tipos de força, incluindo a força elástica segundo a Lei de Hooke, a força resultante, e a força de atrito. A Lei de Hooke estabelece que a deformação de um corpo elástico é diretamente proporcional à força aplicada. A força resultante é a única força equivalente que produz o mesmo efeito que várias forças aplicadas a um corpo. A força de atrito sempre atua no sentido oposto ao movimento e depende do coeficiente de atrito e da força normal de

1. 21
TIPOS DE FORÇA
1 - Força Elástica (Lei de Hooke)
Num corpo elástico, a deformação desaparece quando
se retira a força e num corpo não elástico, a deformação
é permanente. A deformação depende da rigidez do
corpo e da intensidade da força aplicada.
Robert Hooke, mostrou a variação de comprimento dos
corpos elásticos é diretamente proporcional à força
aplicada, dentro de certos limites.
A lei de Hooke é dada por:
F = K . x∆ ; K é a constante elástica (é uma medida da
rigidez do corpo).
Exemplo:
Esse gráfico representa a relação entre a deformação
x e a força F para uma mola. Qual a constante elástica
da mola?
Resolução:
Podemos observar, pelo gráfico, que a relação
x
F
é
constante:
2000
01,0
20
02,0
40
====
x
F
k
Portanto, este é o valor da constante elástica da mola:
k = 2,0 . 10 N/m
2 - Força Resultante
No módulo referente a vetores aprendemos a
determinar o vetor soma ou resultante. Considerando
todas as forças, que atuam sobre um corpo, é possível
substituí-las por uma única força que produziria o
mesmo efeito. Chamamos essa força de Força
Resultante.
Matematicamente, a força resultante é obtida somando
vetorialmente todas as forças aplicadas a ele.
Quando a resultante das forças que agem sobre um
corpo é nula, dizemos que o corpo está em Equilíbrio.
Exemplo:
Determine a força resultante em cada um dos sistemas
a seguir:
a) F1
= 10N
F2
= 20N
Resolução:
As forças 21 e FF
HH
apresentam mesma direção e mesmo
sentido. O módulo da força resultante é a soma dos
módulos de :
R= F1
+ F2
= 10N + 20N = 30N
A direção de é a mesma de : seu sentido é para a
direita.
b) F1
= 50N
F2
= 20N
F3
= 40N
Resolução:
Inicialmente calculamos a resultante das forças 21 e FF
HH
.
3

2. 22
R = F1
– F2
= 50 – 20 = 30N
A seguir, calcula se 3FRR
HHH
+−
3 – Força de Atrito
Um bloco esta em repouso, no plano horizontal, uma
pessoa aplica uma força 1F
H
, mas não consegue move-
lo. Isso se deve à existência de uma força contrária
que equilibra a força aplicada. A essa força,
denominamos Força de Atrito.
“Modelo estático”
Se aumentarmos a força aplicada e observarmos que
o bloco continuou imóvel, podemos concluir que a força
de atrito também aumentou (Fig.2).
Aumentando a força aplicada até que o corpo esteja
na Iminência do movimento, a força de atrito
aumentará até atingir um Máximo.
“Bloco em movimento”
Agora aplicando uma força 4F
H
maior que 3F
H
, o bloco
entregará em movimento. Verificamos que, iniciado o
movimento do corpo, a força necessária para mantê-
lo em movimento é menor que a força de atrito máximo.
Verifica-se experimentalmente que o valor da força de
atrito máximo pe proporcional à força e compressão
( N
H
).
NFat ..max
µ=
→µ Coeficiente de atrito, depende da natureza das
superfícies em contato e do seu grau de polimento.
→µ não depende da área da superfície de contato.
OBS: O coeficiente de atrito cinético é menor que o
estático.
Exemplos:
1 – Um corpo de peso P está apoiado sobre uma
superfície inclinada de um ângulo em relação hori-
zontal. Determine o coeficiente de atrito estático entre
as superfícies, sabendo que o corpo está na iminência
de movimento.
Resolução:
O corpo está sob ação da força peso ( P
H
) e da força de
contato com o plano, que vamos decompor em duas:
força normal ( N
H
) e força de atrito ( atF
H
) orientada para
cima, pois o corpo tende a se mover para baixo. A força
de atrito é máxima pois o corpo está na iminência de
movimento.
Podemos decompor o peso P em duas componentes
nPP e1 nas direções do plano e perpendicular ao plano.
Como o corpo está em equilíbrio, podemos estabelecer
uma igualdade entre os valores das forças opostas:
N = Pn e 1max
PFat =
Projetando P, obtemos:
(
( µ
µ
sen1
cos
PP
PPn
=
=
Daí:
(
( µ
µ
sen
cos
max
PF
PN
at =
=
Podemos então obter ?µ :
µµ
µ
µ
µµ
tg
P
P
N
F
NF
at
at
=
====
?
??
cos
sen
. max
max
2 – Um corpo de 40N de peso está em repouso apoiado
sobre uma superfície horizontal cujo coeficiente de
atrito estático é ?µ = 0,3 e o cinético é cµ = 0,2.
Determine:
a) a força horizontal mínima capaz de fazer o corpo se
mover;
b) a força mínima necessária para manter o corpo em
movimento.
Resolução:
a) A força mínima capaz de fazer o corpo se mover
deve ter intensidade igual à força de atrito estática
máxima:
NFF eat µ== maxmin
→
→
→
N
→
→
F1
→
pt1
→
→
→
N
→
→
F2
→
pt2
→
→
→
→
N→
F2
→
pt2
→
→
→
→
N→
F4
→
fat. cinético

3. 23
sendo N = P, temos N = 40N
Logo:
NFF 1240.3,0 minmin ==−
b) Para manter o corpo em movimento, basta aplicar
uma força F de intensidade igual à força de atrito
cinético:
OBS: A força de atrito é sempre contrária à tendência
de movimento relativo entre as superfícies em contato.
Esta conclusão pode nos levar a acreditar que a força
de atrito sempre procura impedir movimento dos
corpos. Veremos no entanto que, sem a existência do
atrito alguns movimentos seriam impossíveis.
Tomemos como exemplo nossa própria locomoção.
Uma pessoa, para andar, empurra o solo, em sentido
contrário ao do movimento que deseja obter. Devido
ao atrito, o solo reage com uma força de mesma
intensidade e sentido contrário, favorável ao movimento
da pessoa. O atrito, neste caso, é responsável pelo
movimento.

4. 24
EXERCÍCIOS DE FIXAÇÃO
1. Converta em quilogramas as seguintes massas:
a) 0,1g
b) 10g;
c) 100g;
d) 10-3
;
e) 50g;
f) ??
g) 10-2
t;
h) 3t;
i) 106
g.
2. Para cada um dos sistemas a seguir, determine a
intensidade da força resultante:
a)
NF
NF
50
50
2
1
=
=
H
H
b)
NF
NF
15
20
2
1
=
=
H
H
c)
NF
NF
NF
NF
20
30
40
50
4
3
2
1
=
=
=
=
H
H
H
H
d)
NF
NF
3
4
2
1
=
=
H
H
3. Com o propósito de construir um instrumento para
medir a massa de um corpo, foi montado o seguinte
dispositivo: um carrinho que pode conter diversas
massas aferidas é puxado por um fio que passa por
uma polia e está preso a um corpo A, suspenso. O
ponto de partida do carrinho é, para cada experiência,
o mesmo ponto 0. com o auxilio de um cronômetro,
mede-se a duração do trajeto do carrinho até um ponto
B, situado uma distância fixa de 0.
Os resultados obtidos para diversos valores de M (to-
tal da massa aferida) constam desta tabela:
M (g) 0 100 200 300 400 500
T(s) 1,5 1,8 2,1 2,5 2,9 3,5
a) Construa o gráfico de t em função de M.
b) A partir do gráfico, determine o valor de uma massa
M desconhecida, cujo trajeto teve a duração de 3,1s.
4. O comprimento I de uma mola, em função da força
F aplicada à sua extremidade livre, é dado por esta
tabela:
I(cm)12,0 12,5 13,0 13,5 14,0 14,5 15,0 15,5
F(N) 0,0 1,0 2,0 3,0 4,0 5,0 6,0 7,0
a) Construa o gráfico I x F (gráfico de calibração da
mola).
b) Uma força desconhecida faz com que o comprimento
da mola seja de 14,3 cm. Qual o valor dessa força?
5. Qual a força F
H
horizontal mínima, necessária para
colocar na iminência de movimento um corpo em
repouso sobre uma superfície horizontal cujo
coeficiente de atrito estático ? = 0,8 ? O peso corpo é
de 20N.
6. Um corpo de 50N de peso, inicialmente em repouso,
encontra-se apoiado sobre uma superfície horizontal
cujos coeficientes de atrito estático são
respectivamente, ?? = 0,8 ?? = 0,7. Verifique se o corpo
permanecerá em repouso ou entrará em movimento
quando for submetido à ação de uma força horizontal
de intensidade 38N.

5. 25
7. Um corpo em repouso sobre um plano horizontal
esta sendo puxado por uma força F
H
, através de uma
dinamômetro.
Quando o corpo está na iminência de movimento, a
escala do dinamômetro registra 40N. determine o
coeficiente de atrito estático entre as superfícies do
corpo e do plano sendo o peso do corpo de 80N.
8. Os coeficientes de atrito estático e cinético entre as
superfícies de um corpo inicialmente em repouso e
seu apoio horizontal são?????. O peso do corpo é igual
a 100N e ela foi submetida a ação de uma força F
H
horizontal. Determine o valor da força de atrito para
os seguintes valores sucessivos de F:
a) F = 10N
b) F = 30N
c) F = 60N
d) F = 80N
9. Determine o coeficiente de atrito mínimo entre o
corpo A e o plano horizontal, para que os corpos A e B
estejam em repouso.
Dados: ??e10 ? ==∆ PNP
10. Um corpo de peso P encontra-se apoiado sobre
um plano inclinado de um ângulo de 30º em relação à
horizontal. Determine o coeficiente de atrito estático
entre as superfícies do corpo e do plano, sabendo que
o corpo encontra-se na iminência de movimento.
Dados: sen 30º =
2
1
; cos 30º =
2
3
; tg 30º =
3
3
11. O corpo de peso P está sendo puxado por uma
força F
H
de intensidade 50N, paralela à direção do
plano inclinado de ângulo ? em relação a horizontal. O
corpo, nessas condições, está na iminência de
movimento ascendente. Determine o valor da força de
atrito que age no corpo e o coeficiente de atrito estático
entre as superfícies.
Dados: P – 50N; cos ? = 0,8; sen ? = 0,6.
12. No exercício anterior, que valor deve apresentar a
força F
H
para que o corpo esteja na iminência de
movimento descendente?
13. (FCMSCSP) Não é necessária à existência de uma
força resultante atuando:
a) quando se passa do estado de repouso ao de
movimento uniforme;
b) para se manter um objeto em movimento retilíneo
e uniforme;
c) para manter um corpo em movimento circular e
uniforme;
d) para mudar a direção de um objeto sem alterar o
módulo de sua velocidade;
e) em nenhum dos casos anteriores.
14. (CESGRANRIO) Tendo sido danificado em trecho
da estrada, o motorista de um ônibus foi obrigado a
tomar um desvio, conforme indicado na figura.
Ao faze-lo o motorista julgou que não seria necessário
frear e manteve constante a velocidade escalar do
ônibus. Um passageiro, no entanto, reclamou desta
decisão, pois foi “sacudido” de uma extremidade para
outra do banco em que estava sentado. Qual das opções
abaixo indica corretamente em direção de qual
extremidade do banco (direita ou esquerda) o
passageiro foi sucessivamente jogado, ao longo da
trajetória (P.Q.R e S) do ônibus?
P Q R S
A) Direita Esquerda Esquerda Direita
B) Esquerda Direita Direita Esquerda
C) Direita Direita Esquerda Esquerda
D) Esquerda Direita Esquerda Direita
E) Direita Esquerda Direita Esquerda

6. 26
EXERCÍCIOS PROPOSTOS
1. Um plano inclinado forma um ângulo α com o
horizonte. Um corpo é lançado no sentido ascendente
sobre o plano inclinado, com velocidade 0v = 10 m/s.
Sabendo que o coeficiente de atrito entre o corpo e o
plano é 0,5 e que g = 10 m/s2
, determine a distância
percorrida pelo corpo até atingir velocidade nela.
2. (EPUSP) Um plano inclinado liso faz um ângulo de
30º em relação a um plano horizontal áspero. Um corpo
de massa m = 10kg, abandonado no plano inclinado
leva 2 segundos para atingir o plano horizontal.
Determine:
a) À distância percorrida pelo móvel no plano
inclinado.
b) À distância percorrida no plano horizontal, sabendo
que o coeficiente de atrito entre o corpo e plano
horizontal é igual a 0,2.
3. Deixam-se cair simultaneamente, no vácuo, dois
corpos de massa M = 100kg e m = 1kg.
a) qual dos blocos faz força sobre o outro?
b) Qual a aceleração de cada um deles?
4. Um plano horizontal perfeitamente liso é continuado
por um plano rugoso. No plano liso, um corpo em
movimento uniforme percorre a distância de 40m em
4s. O corpo atinge o plano rugoso, percorrendo neste
à distância de 20m até parar. Determine o coeficiente
de atrito entre o corpo e o plano rugoso.
5. Qual velocidade-limite de uma pára-quedista, sendo
sua massa, somada à do pára-quedas, iguais a 100kg,
e admitindo que, para esse conjunto, a força de
resistência do ar é dada por 1F = Kv2
, onde k = 100N =
s2
/m2
e g = 10m/s2
?
6. Determine a força de resistência do ar sobre um
corpo de 10kg de massa, em queda no ar, ao atingir a
sua velocidade-limite. Considere g constante e igual a
10 m/s2
.
7. Para arrastar um bloco sobre uma mesa horizontal,
aqui na terra, devemos fazer uma certa força horizon-
tal, vencendo o atrito cinético para dar ao bloco uma
certa aceleração. Se o corpo e a mesa fossem
transportados para a lua, e fosse aplicado ao bloco a
mesma força, poderíamos afirmar que:
a) o bloco adquiriria maior aceleração porque sua
massa, na lua, seria menor do que na terra;
b) o bloco adquiriria menor aceleração porque a força
de atrito seria maior;
c) o bloco adquiriria a mesma aceleração;
d) o bloco adquiriria maior aceleração porque a força
de atrito seria menor;
e) nenhuma das afirmativas é correta.
8. Um homem de 70 kg de massa se encontra num
elevador, em pé sobre uma balança de molas. A
aceleração da gravidade é g = 10 m/s2
. Determine a
leitura da balança (em Newtons) nos seguintes casos:
a) elevador subindo, com velocidade constante de 2
m/s;
b) elevador descendo, com velocidade constante de 2
m/s2
;
c) elevador subindo acelerado, com aceleração de 1
m/s2
;
d) elevador descendo acelerado, com aceleração de 1
m/s2
;
e) elevador subindo retardado, com aceleração de 1
m/s2
.
9. A figura mostra um elevador, no interior do qual se
pendurou um corpo em um dinamômetro. Quando o
elevador está descendo em movimento uniforme, o
experimentador lê no dinamômetro o valor 8,0N. Ao
atingir o térreo, o elevador breca e a leitura sobe
momentaneamente para 10,0N. Sendo g = 10 m/s2
,
determine vetor-aceleração ao elevador de quanto ele
está brecando módulo, direção e sentido.

7. 27
EXERCÍCIOS DE
APROFUNDAMENTO
1. (FESP) O sistema de dois blocos, ligados por um
fio, é puxado sobre um plano horizontal sem atrito por
uma força constante F
H
, paralela ao plano. A razão
entre os módulos da força e da força de tração no fio
AB é:
a) 1;
b) 2;
c)
2
1
;
d)
2
3
.
2. (PUCC-SP) Sobre um carrinho de massa m= 2kg
atuam as forças colineares 1F = 15N e 2F = 5N,
conforme indica a figura. Admitindo-se ausência de
atrito, a aceleração resultante do carrinho, em m/s2
,
será:
a) 2,5;
b) 5,0;
c) 7,5;
d) 10;
e) 12.
3. (CESGRANRIO) A figura representa
esquematicamente uma composição ferroviária com
uma locomotiva e três vagões idênticos, movendo-se
com aceleração constante a
H
. Sejam 321 e, FFF os
módulos das forças exercidas por cada uma das barras
de acoplamento (1), (2) e (3), respectivamente, sobre
os vagões. Se as forças de atrito exercidas sobre os
vagões forem desprezíveis, podemos afirmar que:
a) 321
2
1
3
1
FFF == ;
b) 321
3
1
2
1
FFF == ;
c) 321 FFF == ;
d) 321 32 FFF == ;
e) 321 23 FFF == .
4. (EEM-SP) Um motorista de um automóvel, viajando
por um trecho reto e plano de uma estrada, percebe
um obstáculo a 200 m de distância. Aplica os freios
de tal modo que o veículo adquire a máxima aceleração
de retardamento possível e consegue parar junto ao
obstáculo. O coeficiente de atrito entre as rodas do
automóvel e o pavimento é 0,2 e o peso daquele é de
9.800N. o automóvel pode ser considerado ponto
material e g = 9,8 m/s2
. Determine:
a) a aceleração do retardamento do veículo;
b) a velocidade,em km/h, que o mesmo desenvolve
no início da freada;
c) o tempo que o mesmo levou até parar.
5. (CESCEM-SP) O coeficiente de atrito de C sobre B é
0,2. O coeficiente de atrito de B sobre A é 0,05. São
dados: ma
= 10 kg, mc
= 5 kg e g = 10 m/s2
. Se o corpo C
é puxado com uma força F = 5N:
a) C desliza sobre B, mas B não desliza sobre A;
b) C não desliza sobre B, mas B desliza sobre A;
c) C não desliza sobre B e B não desliza sobre A;
d) C desliza sobre B e B desliza sobre A;
e) C desliza sobre B e B desliza sobre A em sentido
contrário.
6. (VUNESP) Uma locomotiva de massa igual a 5,0
velocidade de 72 km/h. Em dado momento ela enfrenta
uma obstrução na linha devida a um desabamento do
barranco. Sem que o maquinista acione qualquer
comando, ele vence a barreira em 5,0s, reduzindo sua
velocidade à metade.
a) calcule a força média exercida pela barreira sobre
a locomotiva;
b) explique os princípios físicos envolvidos.
7 – (FEI-SP) Pesa-se um corpo com um dinamômetro
preso ao forro de um elevador. Com este em repouso
ou em movimento, as leituras do dinamômetro são
respectivamente Pr
e Pm
. Podemos afirmar:
a) rm PP > , se o elevador subir em movimento
retardado;

8. 28
b) rm PP > , se o elevador descer em movimento
retardado;
c) rm PP > , se o elevador subir em movimento uniforme;
d) rm PP > , se o elevador descer em movimento
uniforme;
e) rm PP = , qualquer que seja o movimento do elevador.
8. (FAAP-SP) Tem-se mA
= 1 kg e mg
= 4 kg. O fio e a
polia são ideais e o atrito é desprezível. Calcule a
velocidade dos blocos 2s após terem sido abandonados.