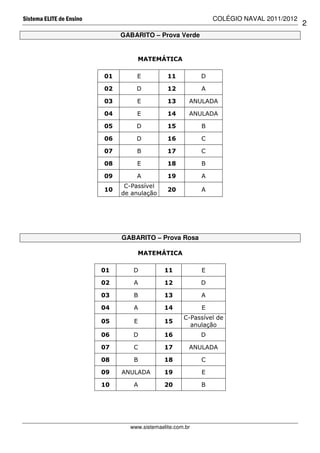
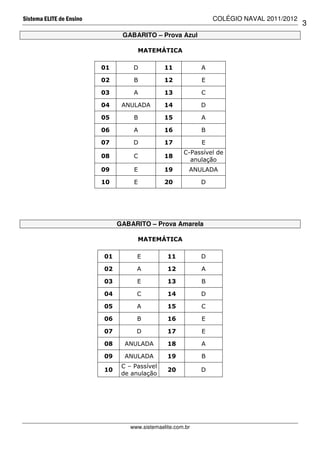
Este documento contém quatro gabaritos de provas de matemática realizadas no Colégio Naval em 2011/2012. Cada gabarito lista as questões e suas respectivas alternativas corretas. Além disso, um dos gabaritos é comentado, explicando a resolução de algumas questões.