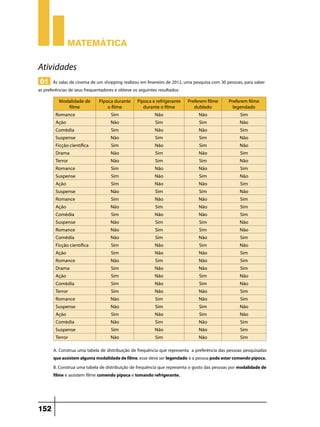
Este documento apresenta 50 aulas sobre conteúdos de matemática do 9o ano do ensino fundamental. As aulas abordam tópicos como conjuntos numéricos, operações com números naturais, racionais e reais, potenciação, radiciação, razão e proporção, perímetro e área de figuras planas e sólidas, e estatística. Há também exercícios para fixação dos conceitos apresentados.

1. Caderno
Caderno
educacional
educacional
Material do professor
Material do professor
Material do professor
MATEMÁTICA
Ciências
ciências
Material de apoio
Material de apoio
9
o
ano

2. Expediente
Marconi Ferreira Perillo Júnior
Governador do Estado de Goiás
Thiago Mello Peixoto da Silveira
Secretário de Estado da Educação
Erick Jacques Pires
Superintendente de Acompanhamento de Programas Institucionais
Raph Gomes Alves
Chefe do Núcleo de Orientação Pedagógica
Valéria Marques de Oliveira
Gerente de Desenvolvimento Curricular
Gerência de Desenvolvimento Curricular
Elaboradores
Abadia de Lourdes da Cunha
Alexsander Costa Sampaio
Aline Márcia dos Santos
Carlos Roberto Brandão
Deusite Pereira dos Santos
Inácio de Araújo Machado
Júnior Marques Carneiro
Lidiane Rodrigues da Mata
Márcio Dias de Lima
Marlene Aparecida Faria
Mônica Martins Pires
Regina Alves Costa Fernandes
Silma Pereira do Nascimento Vieira

3. Sumário
Apresentação...............................................................................................................................................5
Aula 01 Conjunto dos Números Naturais (N )........................................................................7
Aula 02 Conjunto dos números inteiros (Z ) – Operações............................................10
Aula 03 Conjunto dos Números Racionais (Q ) – Frações..............................................14
Aula 04 Conjunto dos números racionais (Q ) Números
Decimais – Operações..................................................................................................19
Aula 05 Conjunto dos números racionais (Q ): Equivalência de frações..................23
Aula 06 Conjunto dos números racionais (Q ) – Conversão..........................................27
Aula 07 Conjunto dos Números Irracionais.........................................................................30
Aula 08 Conjunto dos Números Reais (R ) ..........................................................................32
Aula 09 Os números racionais na reta numérica...............................................................35
Aula 10 Potenciação: Definição................................................................................................37
Aula 11 Potenciação: Propriedades........................................................................................41
Aula 12 Potência com expoente negativo...........................................................................43
Aula 13 Potenciação: expressões numéricas.......................................................................46
Aula 14 Decomposição em fatores primos..........................................................................48
Aula 15 Radiciação: Definição / Extração de raiz...............................................................50
Aula 16 Radiciação (propriedades).........................................................................................55
Aula 17 Radiciação inexata .......................................................................................................58
Aula 18 Relacionando potências e radicais..........................................................................60
Aula 19 Resolução de situações problema envolvendo números R .........................62
Aula 20 Exercícios – números Reais........................................................................................64
Aula 21 Rotação de polígonos – Propriedades..................................................................66
Aula 22 Reflexão de polígonos – Propriedades..................................................................70
Aula 23 Translação de polígonos – Propriedades.............................................................75
Aula 24 Plano Cartesiano Ortogonal......................................................................................79
Aula 25 Construção de polígonos no plano cartesiano..................................................83
Aula 26 Exercícios envolvendo polígonos............................................................................88
Aula 27 Circunferência e círculo: Definição e diferenças...............................................90
Aula 28 Razão I................................................................................................................................94
Aula 29 Razão II (situações problema envolvendo razões em porcentagens) ����100
Aula 30 Proporção ......................................................................................................................104

4. Aula 31
Aula 32
Aula 33
Aula 34
Aula 35
Aula 36
Aula 37
Aula 38
Aula 39
Aula 40
Aula 41
Aula 42
Aula 43
Aula 44
Aula 45
Aula 46
Aula 47
Aula 48
Aula 49
Proporção – Propriedade..........................................................................................111
Exercícios envolvendo razão e proporção.........................................................117
Perímetro de polígonos diversos...........................................................................118
Área de polígonos: quadrados e retângulos....................................................123
Área de polígonos – Triângulos.............................................................................126
Área de polígonos: paralelogramo.......................................................................131
Área de polígonos: trapézio....................................................................................135
Área de polígonos: pentágono e hexágono.....................................................138
Área de superfície de figuras não planas: cubo, cilindro
e paralelepípedo..........................................................................................................142
Exercícios envolvendo a área de superfície de figuras não planas:
cubo, cilindro e paralelepípedo, aplicados em avaliações externas........146
Leitura de gráficos e tabelas...................................................................................150
Construir tabelas de dados estatísticos..............................................................155
Construir gráficos de frequência de dados estatísticos – coluna.............161
Construção de gráficos de frequência de dados estatísticos – barra �����166
Construção de gráficos de frequência de dados estatísticos
– setores..........................................................................................................................172
Conclusões com base na leitura de gráficos.....................................................177
Relacionar gráficos com tabelas............................................................................181
Relacionar tabelas com gráficos............................................................................187
Conclusões com base na leitura de tabelas......................................................195

5. Apresentação
O Governo do Estado de Goiás, por meio da Secretaria de Estado da Educação (SEDUC), criou o “Pacto pela Educação com o objetivo de avançar na
”
oferta de um ensino qualitativo às crianças, jovens e adultos do nosso Estado.
Assim, busca-se adotar práticas pedagógicas de alta aprendizagem.
Dessa forma, estamos desenvolvendo, conjuntamente, várias ações, dentre
elas, a produção deste material de apoio e suporte. Ele foi concebido tendo por
finalidade contribuir com você, professor, nas suas atividades diárias e, também, buscando melhorar o desempenho de nossos alunos. Com isso, espera-se
amenizar o impacto causado pela mudança do Ensino Fundamental para o
Médio, reduzindo assim a evasão, sobretudo na 1ª série do Ensino Médio.
Lembramos que a proposta de criação de um material de apoio e suporte
sempre foi uma reivindicação coletiva de professores da rede. Proposta esta
que não pode ser viabilizada antes em função da diversidade de Currículos que
eram utilizados. A decisão da Secretaria pela unificação do Currículo para
todo o Estado de Goiás abriu caminho para a realização de tal proposta.
Trata-se do primeiro material, deste tipo, produzido por esta Secretaria,
sendo, dessa forma, necessários alguns ajustes posteriores. Por isso, contamos
com a sua colaboração para ampliá-lo, reforçá-lo e melhorá-lo naquilo que for
preciso. Estamos abertos às suas contribuições.
Sugerimos que este caderno seja utilizado para realização de atividades dentro e fora da sala de aula. Esperamos, com sua ajuda, fazer deste um objeto de
estudo do aluno, levando-o ao interesse de participar ativamente das aulas.
Somando esforços, este material será o primeiro de muitos e, com certeza,
poderá ser uma importante ferramenta para fortalecer sua prática em sala de
aula. Assim, nós o convidamos para, juntos, buscarmos o aperfeiçoamento de
ações educacionais, com vistas à melhoria dos nossos indicadores, proporcionando uma educação mais justa e de qualidade.
A proposta de elaboração de outros materiais de apoio continua e a sua
participação é muito importante. Caso haja interesse para participar dessas elaborações, entre em contato com o Núcleo da Escola de Formação pelo e-mail
cadernoeducacional@seduc.go.gov.br
Bom trabalho!
5

7. Matemática
Aula 01
Conjunto dos Números Naturais (N)
Objetivo geral
Relembrar as quatro operações (adição, subtração,
multiplicação, divisão) do conjunto dos números naturais.
O que devo aprender
nesta aula
Conceito básico
u Reconhecer a aplicação
Os números naturais surgiram da necessidade de fazer
contagens, portanto, fica claro que tal conjunto é formado
pelos números que utilizamos para contar. Representa-se
o conjunto dos números naturais por N :
N = "0, 1, 2, 3, ... ,
u
A seguir faremos uma pequena revisão acerca das
operações de adição, subtração, multiplicação e divisão
trabalhadas no conjunto N .
Adição: É a operação matemática que permite juntar e/
ou acrescentar quantidades. Tais quantidades são chama­
das termos ou parcelas. A operação 2 936 + 4 652 = 7 588
indica uma adição.
dos números naturais e suas
diferentes formas de utilização
no cotidiano.
Reconhecer e aplicar as
propriedades das operações
com números naturais e
percebê-las como facilitadoras
na compreensão das técnicas
operatórias.
u Analisar, interpretar, formular
e resolver situações problema
em diferentes contextos sociais
e culturais.
Subtração: É a operação matemática que permite retirar certa quantidade de outra. Tais
quantidades, também, são chamadas termos ou parcelas. A operação 1527 – 1354 = 173 indica
uma subtração.
Multiplicação: É a operação matemática que permite adicionar quantidades iguais. O
resultado de uma multiplicação é chamado de produto. A operação 12 . 46 = 552 indica uma
multiplicação.
Divisão: É a operação matemática que permite repartir um número em quantidades iguais. A
operação 1554 ' 37 = 42 indica uma divisão.
Propriedades importantes da adição e da multiplicação
Quando trabalhamos com a adição ou a multiplicação de números naturais existem algumas
propriedades comuns que devem ser relembradas. São elas:
Comutativa: A ordem das parcelas não altera o resultado final da operação.
Adição: a + b = b + a
Exemplo: 5 + 7 = 12 e 7 + 5 = 12, portanto, 5 + 7 = 7 + 5.
7

8. Matemática
Multiplicação: a . b = b . a
Exemplo: 5 . 7 = 35 e 7 . 5 = 35, portanto, 5 . 7 = 7 . 5 = 35.
Associativa: O agrupamento das parcelas não altera o resultado.
Adição: (a + b) + c = a + (b + c)
Exemplo: (2 + 3) + 5 = 5 + 5 = 10 e 2 + (3 + 5) = 2 + 8 = 10, portanto, (2 + 3) + 5 = 2 + (3 + 5)
Multiplicação: (a . b) . c = a . (b . c)
Exemplo: (3 . 4) . 2 = 12 . 2 = 24 e 3 . (4 . 2) = 3 . 8 = 24, portanto, (3 . 4) . 2 = 3 . (4 . 2)
Observação: Quando temos uma expressão envolvendo parênteses, devemos realizar primei­
ramente as operações contidas em seu interior.
Expressão Numérica
Na expressão numérica, os sinais de associação devem seguir a ordem: os parênteses ( ) devem
ficar dentro dos colchetes [ ], e estes, dentro das chaves { }.
Nesse caso, deve-se efetuar primeiro as operações que estão entre parênteses, em seguida as
operações que estão nos colchetes e, finalmente, as que estiverem entre chaves.
Em relação as operações matemáticas devemos obedecer a seguinte ordem: multiplicação e/
ou divisão e, em seguida, adição e/ou subtração. Por exemplo:
8+5.3=
(I)
8 + 15 =
23
( II )
15 + [(3 . 6 - 2) - (10 - 6 : 2) + 1] =
15 + [(18 - 2) - (10 - 3) + 1] =
15 + [16 - 7 + 1] =
15 + [9 + 1] =
15 + 10 =
25
Atividades
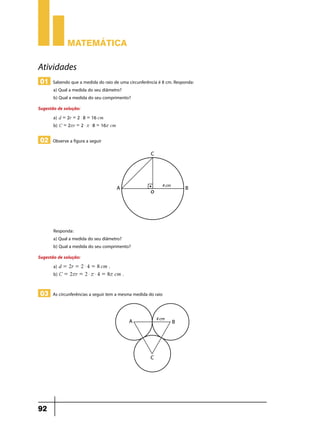
01 Efetue cada uma das operações a seguir:
a) 487 + 965
b) 1238 – 649
8

9. Matemática
c) 35 . 126
d) 9114 : 62
Sugestão de solução:
a) 1452; b) 589; c) 4410; d) 147.
02 Calcule o valor das seguintes expressões numéricas:
a) 50 – {15 + [16 : (10 – 2) + 5 . 2]} =
b) 70 – [5 . (4 : 4) + 9] =
c) 25 + {27 : 9 + [9 . 5 – 3 . (8 – 5)]} =
d) 25 – [27 – (4 – 1 + 6 – 4)] =
Sugestão de solução:
a) 23; b) 56; c) 64; d) 3.
03 Resolva os probleminhas a seguir:
a) Um pai deixou de herança para seus 3 filhos uma coleção com 3.216 selos de diversos países. Supondo uma divisão equilibrada, quantos selos caberão a cada filho?
(Desenvolva o algoritmo da divisão).
b) Antônio recebe R$ 35,00 de mesada de seu pai. Quanto ele terá recebido depois de 1 ano e meio?
c) Maria levou R$ 20, 00 para fazer compras no supermercado. Ela gastou R$ 5,00 com bolachas e chocolates e R$
9,00 com produtos de limpeza. Quantos reais sobraram para Maria?
d) Um funcionário precisa colocar 336 latas de refrigerantes em caixas de papelão. Se em cada caixa cabem 16 latas,
quantas caixas serão necessárias para armazenar todas as latas de refrigerante?
Sugestão de solução:
a) 1 072 selos; b) R$ 630,00; c) R$ 6,00; d) 21 caixas.
Desafio
Sabendo que Tiago tem uma coleção composta por 396 figurinhas, responda:
a) Se Tiago dividir suas figurinhas com seu primo Mateus em duas partes exatamente iguais, quantas
figurinhas terá cada um?
b) Se Tiago triplicar sua coleção a nova quantidade corresponderá a que valor?
c) Caso o pai de Tiago lhe dê mais 89 figurinhas qual será a nova quantidade obtida por ele?
d) Se Tiago der 129 figurinhas a Lucas, quantas figurinhas lhe sobrarão?
Sugestão de solução:
a) 198; b) 1 188; c) 485; d) 267.
9

10. Matemática
AULA 02
Conjunto dos números
inteiros (Z) – Operações
Objetivo Geral
Interpretar e resolver situações problema envolvendo
operações com números inteiros.
Conceitos Básicos
u Reconhecer a importância
O conjunto dos números inteiros ( Z ) encontra-se
presente em diversas situações do dia-a-dia, principalmente
quando apresentam o envolvimento de números negativos.
É formado pela união do conjunto dos números naturais
com os seus simétricos em relação ao zero. Portanto, é
formado por números positivos e negativos:
Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Dois números são ditos simétricos quando sua soma
for igual a zero. Portanto, dizemos que os números
negativos (-1, -2, -3, ...) são simétricos dos números
naturais, uma vez que:
1 + (-1) = 0,
O que devo aprender
nesta aula
2 + (-2) = 0,
3 + (-3) = 0
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.
Operações com Números Inteiros
As operações que envolvem os números inteiros requerem a utilização de regras matemáticas
envolvendo os sinais positivos (+) e negativos (–). Para isso é necessário que fique claro que
operação matemática está sendo desenvolvida: adição ou multiplicação.
Adição de números inteiros
É importante perceber que a expressão adição de números inteiros é utilizada quando há a
sequenciação de números positivos e negativos sem que haja as operações de multiplicação e/ou
divisão. Para isso é importante observar se as parcelas à serem operadas possuem sinais iguais ou
diferentes. Assim:
10

11. Matemática
 as parcelas possuírem sinais iguais o resultado final terá o mesmo sinal das parcelas e
Se
será obtido a partir da adição das mesmas, não importando se ambas forem positivas ou
negativas. Observe:
a) - 20 - 25 =- 45
b) 32 + 17 =+ 32 + 17 =+ 49 = 49
 as parcelas possuírem sinais diferentes o resultado final terá o sinal da parcela que
Se
possuir o maior valor absoluto e será obtido a partir da subtração das mesmas. Observe:
a) - 25 + 45 =+^ 45 - 25h =+ 20
b) 38 - 51 =- (51 - 38) =- 13
Multiplicação e ou divisão de números inteiros
Para operarmos a multiplicação ou a divisão de dois números inteiros assim como na adição de
números inteiros inicialmente é necessário perceber o sinal das parcelas à serem operadas. Assim:
 produto ou o quociente de duas parcelas que possuem o mesmo sinal é um número
O
positivo.
a) (- 6) $ (- 18) =+ 108 = 108
b) (5) $ (9) = (+ 5) $ (+ 9) =+ 45 = 45
c) (- 90) ' (- 15) =+ 6 = 6
d) (170) ' (17) = (+ 170) ' (+ 17) =+ 10 = 10
 produto ou quociente de dois números de sinais diferentes é um número negativo.
O
a) (- 8) $ (+ 9) =- 72
b) (+ 7) $ (- 13) =- 91
c) (- 45) ' (+ 5) =- 9
d) (+ 100) ' (- 10) =- 10
Atividades
01 Uma microempresa representou em um gráfico seus resultados do segundo semestre do ano.
11

12. Matemática
Atenção: Os números positivos indicam o lucro da empresa e os negativos indicam o prejuízo da empresa.
Analisando os dados do gráfico responda:
a) Em quais meses a microempresa teve lucro?
b) Em quais meses a microempresa teve prejuízo?
c) Em qual mês a microempresa apresentou o pior resultado? Porque?
d) Qual foi o lucro médio nesses semestre?
e) Contabilizando o lucro e o prejuízo total desta empresa nos seis meses apresentadas determine se a
empresa terminou com saldo positivo ou negativo? Qual foi o montante deste saldo?
Sugestão de solução:
a) Nos meses de agosto, outubro e dezembro.
b) Nos meses de julho, setembro e novembro.
c) No mês de novembro.
d) Lucro. 12 milhões.
e) 2 milhões.
12

13. Matemática
02 Observe o saldo bancário de Gabriel relativo aos meses de março a junho.
Mês
Março
Abril
Maio
Junho
Saldo
+ R$ 800,00
+ R$ 250,00
- R$ 150,00
- R$ 950,00
Qual é o saldo do Gabriel ao final desses quatro meses?
Sugestão de solução:
- 50 reais
03 Imagine uma sequência numérica onde o primeiro termo é o número (–8). Então:
a) Determine o segundo termo desta sequência sabendo que ele é o dobro do primeiro mais quatro.
b) Determine o terceiro termo desta sequência sabendo que ele é igual ao triplo do primeiro termo menos dez.
c) Determine o quarto termo desta sequência sabendo que ele é igual ao quádruplo do primeiro menos cinco.
d) Determine o sexto termo desta sequência sabendo que ele é igual ao quíntuplo do primeiro dividido por
menos quatro (-4).
Sugestão de solução:
a) -12; b) -34; c) -37; d) 10.
04 Em uma operação onde o resto é 0 e o dividendo é + 72 , o quociente é - 8. Qual é o divisor?
Sugestão de solução:
9
Desafio
Em um campeonato de damas ficou estabelecido o seguinte critério de pontuação:
Vitória
Empate
Derrota
+ 5 pontos
+ 3 pontos
- 2 pontos
Paulo terminou a primeira fase do campeonato com 30 pontos e, na segunda fase atingiu 3 vitórias, 1
empate e 2 derrotas.
Marcos, por sua vez, terminou a primeira fase do campeonato com 32 pontos e, na segunda fase atingiu
1 vitória, 2 empates e 3 derrota.
13

14. Matemática
Responda:
a) Quantos pontos Paulo e Marcos alcançaram, respectivamente, ao final da 2ª fase do campeonato?
b) Quem foi o ganhador?
Sugestão de solução:
a) Paulo 44 pontos e Marcos 37 pontos.
b) Paulo.
Aula 03
Conjunto dos Números Racionais (Q )
Frações
Objetivo Geral
Compreender a ideia de fração (parte-todo), razão e
divisão;
Efetuar cálculos e resolver situações problema que
envolvam as operações com números racionais na forma
fracionária.
O que devo aprender
nesta aula
u Compreender as frações
e utilizá-las em situações
diversas.
u Formular e resolver situações
Conceito básico
Os números racionais são os que podem ser escritos na
forma de fração a , em que a e b são números inteiros e b
b
! zero.
problema que envolva a
ideia de fração (parte-todo) e
também de razão e divisão.
O conjunto dos números racionais (representado por
Q ) é definido por:
a
a ! Z;b ! Zeb
Q=$
b
! 0.
Em outras palavras, o conjunto dos números racionais é formado por todos os quocientes de
números inteiros a e b, em que b é não nulo. Exemplos:
3 (lê-se: três décimos)
10
14
0 (é o mesmo que 0 )
1

15. Matemática
4 (lê-se: quatro quintos)
5
- 3 (é o mesmo que - 3 )
1
13 (lê-se: treze vinte avos)
20
- 8 (é o mesmo que 8 )
5
5
Fração
Fração é a parte de um todo. Em sua representação há o numerador e o denominador.
Significado
Numerador
Número colocado acima do traço que indica quantas partes da
unidade foram tomadas.
Denominador
Número colocado abaixo do traço que indica em quantas partes
iguais a unidade foi dividida.
Exemplo 1:
Observe a figura:
Ela representa uma pizza dividida em 8 pedaços iguais.
Cada pedaço representa uma fração da pizza, que é indicado
por 1 .
8
Como foram colocados em destaque dois pedaços, podemos
repre­ entá-los pela fração 2 .
s
8
Exemplo 2:
João pegou na biblioteca da escola um livro de 34 páginas para ler. Até o momento João leu
22 paginas.
Qual a fração que representa o número de páginas que João leu?
Para a resolução do problema, temos que identificar o conjunto universo, que neste caso é o
total de páginas do livro, ou seja, 34.
O total de páginas lidas por João é 22.
Logo a fração correspondente às páginas lida será: 22 .
34
15

16. Matemática
Operações com frações
Adiçao e subtração
Dividiu-se um hexágono em 6 partes iguais e pintou-se de vermelho 2 dessas partes, e de rosa,
outras 3, conforme figura abaixo.
Nesta condição podemos dizer que 2 do hexágono está pintado de vermelho e 3 está pintado
6
6
de rosa.
Assim, observando a figura temos que das 6 partes do hexágono, 5 estão pintadas.
Logo podemos dizer que no total, 5 do hexágono está pintado.
6
2 +3 = 5
Concluímos que:
6 6 6
Na soma ou subtração de frações com denominadores iguais, basta conservar o denominador
e operar os numeradores (somar ou subtrair).
Exemplos:
a) 3 + 8 = 11 (ou seja, 1 inteiro) b) 2 + 7 = 9
11 11 11
17 17 17
c) - 2 + 3 = 1 d) 5 - 3 = 2
6 6 6
9 9 9
e) 3 - 4 =- 1
5 5
5
Multiplicação e divisão
Observe a figura a seguir:
16

17. Matemática
Considerando o triplo da área pintada da figura acima teremos:
2 6
Assim, a parte pintada corresponde a 6 do retângulo. Logo, 3 $ = .
8 8
8
3
Lembre-se que todo numero inteiro pode ser escrito na forma de fração, assim 3 = .
1
Logo, 3 $ 2 = 6 , pois, 3 $ 2 = 6 .
1 8 8
1$8
8
O resultado de uma multiplicação entre duas frações é uma fração cujo numerador é o
produto dos numeradores e cujo denominador é o produto dos denominadores.
Para dividir duas frações, temos que:
O quociente de uma fração por outra é igual ao produto da primeira fração pelo inverso
da segunda fração.
Exemplos:
3 '5
2 4
&
3 ' 4 = 12
2 5 10
2 '1
5 3
&
2 '3 = 6
5 1
5
Atividades
01 Observe as figuras abaixo
Que fração a parte pintada representa em cada figura? Escreva por extenso.
Sugestão de soluçao:
17

18. Matemática
02 A mãe de Fabrício fez um delicioso bolo. Ela tinha uma dúzia de ovos, e, para fazer o bolo utilizou 4 ovos. Que
fração representa os ovos que sobraram? Qual o denominador dessa fração? E o numerador?
Sugestão de solução
12 – 4 = 8
A fração que representa os ovos que sobraram é:
O denominador é 12, e o numerador é 8.
8
12
.
03 Calcule
a)
1 2 = b) 2 3 = c) 3
5 =
'
$
$
5 4
3 5
2
6
Sugestão de solução:
a)
1 2 = 2
$
5 4
20
b)
2 3 = 6
$
3 5
15
c)
04 Amanda tem 15 anos. A idade de sua prima é
Quantos anos tem a prima de Amanda?
2
5
3 6 = 18
$
2 5
10
de sua idade.
Sugestão de solução:
2
5
de 15 = 15 : 5 = 3, 2 partes equivale a 6.
A prima de Amanda tem 6 anos.
05 Maurício leu 15 páginas de uma revista. Desse modo, Maurício leu
ta de Maurício?
Sugestão de solução:
A revista tem 25 páginas.
06 Efetue a seguinte operação:
a)
2
1
6
2 3
' $ $ 8 - ` + jB. =
3
2 7
7 7
Sugestão de solução:
2
1
6 5
' $ $ 8 - B. =
3
2 7 7
2
1 1
'$ $ . =
3
2 7
2
1
'
3 14
18
=
2 14
$
3 1
=
28
3
3
5
da revista. Quantas páginas tem a revis-

19. Matemática
Desafio
Marina ganhou certa quantia de dinheiro de sua mãe, dessa quantia ela gastou
tes. Do que sobrou, ela gastou 1 com pirulitos.
2
5
comprando chocola-
2
Que fração do dinheiro que Marina ganhou foi gasto com pirulitos?
Sugestão de solução:
3
10
Aula 04
Conjunto dos números racionais (Q )
Números Decimais – Operações
Objetivo Geral
Operar com números decimais e resolver situações
problema do cotidiano envolvendo as operações com
números decimais.
Conceito básico
Um número é dito decimal quando apresentar uma
vírgula em sua escrita. Por exemplo 3,7 .
Para ler o número escrito na forma decimal
primeiramente faz-se a leitura do número como se
não existe vírgula. Assim, no número 14,2 lê-se cento e
quarenta e dois.
O passo seguinte é especificação da parte decimal. Para
isso basta seguir as seguintes orientações:
 Se houver apenas um número após a vírgula será
usada a expressão décimos.
u 1,4 (lê-se: quatorze décimos)
 Se houverem dois números após a vírgula será
usada a expressão centésimos.
u 1,13 (lê-se: cento e treze centésimos)
O que devo aprender
nesta aula
u Reconhecer a importância
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.
19

20. Matemática
 Se houverem três números após a vírgula será usada a expressão milésimos.
u 2,075 (lê-se: dois mil e setenta e cinco milésimos).
É válido salientar que todo número escrito na forma de fração pode ser escrito como decimal.
Para isso basta dividir o numerador pelo denominador. Veja os exemplos:
3 =
0, 3
10
- 11 =- 1, 22222.......
9
4 =
0, 8
5
71 =
0, 71
100
13 =
0, 65
20
8 =
1, 6
5
Este processo é extremamente importante para auxiliar na localização de um número racional
na reta numérica.
Para transformar um número decimal em uma fração decimal, escreve-se uma fração cujo
numerador é o numero decimal sem vírgula, o denominador será o algarismo um (1) seguido de
tantos zeros quanto forem as casas decimais do número decimal dado.
Exemplos:
1, 22
duas casas
=
122
13
0, 013 =
100
1000
3
0, 3 =
10
dois zeros
Comparando dois números decimais
Para comparar dois números decimais é necessário, primeiramente, igualar as casas decimais
dos dois, acrescentando zeros á direita do número que possuir menor quantidade de algarismos.
Em seguida, é preciso eliminar a vírgula de ambos. Após o desenvolvimento destas duas etapas
faz-se a comparação dos produtos finais.
Exemplos:
Vamos comparar os números 0,197 e 0,0987, usando os sinais: < (menor), > (maior) ou =
(igual).
0, 0987
S
4 casas
0, 1970
S
acrescenta-se um zero para igualar as casas decimais com o outro número
Elimina-se a vírgula dos dois números e os compara:
987 e 1970 " 987 < 1970.
Logo, 0,0987 < 0,197
20

21. Matemática
Operações com números decimais
Adição e subtração
Para somar ou subtrair dois números decimais, primeiramente, é preciso acrescentar quantos
zeros forem precisos para igualar o número de casas decimais de ambos:
2, 7 + 3, 0456
2, 7 + 3, 0456
" 2, 7 + 3, 0 456
S
"
3 casas a mais
2, 7 000
S
+ 3, 0456
3 casas completadas com o 0
Mesma quantidade de casas decimais
6 44 ?
4
4
? 7 44 8
2, 7000 + 3, 0456
O passo seguinte será a organização do algoritmo de forma que ambos fiquem com suas
respectivas vírgulas uma embaixo da outra.
Vírgula debaixo
de vírgula
.
2, 7000
+ 3, 0456
Desta forma realiza-se a operação identificada (adição ou subtração) colocando o resultado
com sua respectiva vírgula alinhada com as anteriores.
Vírgula debaixo
de vírgula
.
2, 7000
+ 3, 0456
5, 7456
Multiplicação
Para multiplicar dois números decimais primeiramente multiplica-se ambos omitindo a
vírgula do processo.
3, 21
# 2, 4
1284
642 +
7704
No resultado obtido coloca-se a vírgula na casa decimal correspondente ao resultado da soma
das casas decimais das parcelas da multiplicação.
21

22. Matemática
3, 21
# 2, 4
"
"
Duas casas após a vírgula
Total de três casas decimais
Uma casa após a vírgula
1284
642 +
7 704
3, 21
# 2, 4
1284
642 +
7, 704
Divisão
O procedimento inicial para dividir dois números decimais assemelha-se ao utilizado na adição
e subtração de números decimais uma vez que é necessário igualar as casas decimais das parcelas.
Assim, para dividir o número 4,7 pelo número 2,35 será necessário igualar a quantidade de
casas decimais do primeiro número com a quantidade de casas decimais do segundo.
Portanto,
Uma casa
decimal
4, 7 2, 35
"
?
Duas casas
decimais
?
4, 7 2, 35
"
Mesma quantidade
de casas decimais
?
?
4, 70 2, 35
"
4, 70 2, 35
A etapa seguinte consiste em eliminar as vírgulas de ambas as parcelas (dividendo e divisor) e
desenvolver o algoritmo da divisão.
4, 70 2, 35
"
470 235
Atividades
01 Efetue as operações a seguir:
a) 2,47 + 0,0165
b) 3 – 1,276
c) 4 x 2,195
d) 66 : 2,2
e) 32,51 + 0,4
f) 13,31 – 2,3
g) 5,2 x 2,3
h) 4,50 : 1,5
Sugestão de solução:
a) 2,4865; b) 1,724; c) 8,78; d) 30; e) 32,91; f) 11,01; g) 11,96; h) 3.
22

23. Matemática
02 Dona Ângela foi ao supermercado fazer compras e levou consigo R$ 50,00. Comprou 3 latas de milho que custam
R$ 1,15 cada uma, 1 pacote de macarrão que custa R$ 2,10 e 2 kg de carne que custam R$ 9,80 cada quilo.
a) Quanto ela gastou no supermercado?
b) Com o total do troco dona Ângela comprou 3,5 metros de tecido par fazer cortinas. Quanto custa o metro
desse tecido?
Sugestão de solução:
a) R$ 25,15; b) R$ 7,10.
03 Uma fábrica de refrigerantes produz 55 litros de refrigerante por hora e deseja encher garrafas com 2,5 litros
cada uma. Quantas garrafas serão utilizadas em uma hora?
Sugestão de solução:
22 garrafas
Desafio
(UFRJ) Em uma viagem ao exterior o carro de um turista brasileiro consumiu, em uma semana, 50 galões
de gasolina, a um custo total de 152 dólares. Considere que um dólar, durante a semana da viagem, valia
1,60 reais e que a capacidade do galão é de 3,8 L.
Durante essa semana, o valor, em reais, de 1 L de gasolina era de:
a) 1,28
b) 1,40
c) 1,75
d) 1,90
Sugestão de solução:
Letra a
Aula 05
Conjunto dos números racionais (Q ):
Equivalência de frações
Objetivo geral
Relembrar o conceito de frações equivalentes.
23

24. Matemática
Conceito básico
Pode-se falar que duas ou mais frações são equivalentes
se estas representam a mesma quantidade de uma grandeza.
O que devo aprender
nesta aula
u Reconhecer a importância
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
Observe que nas duas figuras a parte pintada é a mesma.
Daí, conclui-se que as frações 2 e
4
1 representam a
2
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.
mesma quantidade, logo, são frações equivalentes, e podem
ser indicadas como: 2 = 1 , ou, 2 + 1 .
4
2
4
2
Portanto, dizemos que duas ou mais frações são equivalentes quando corresponderem à
mesma quantidade.
Exemplo:
Ana e Maria ganharam duas pizzas do mesmo tamanho. Ana dividiu sua pizza em 8 partes
iguais e comeu 4 delas. Maria dividiu a sua em 4 partes iguais e comeu duas partes. Quem comeu
mais pizza?
24

25. Matemática
A partir das ilustrações fica perceptível que 2 e 4 representam a mesma quantidade, logo,
4
8
as frações são equivalentes. Podemos concluir, então, que ambas comeram a mesma quantidade
de pizza.
Para saber se duas frações são equivalentes, há um método extremamente simples: basta
multiplicar o numerador da primeira fração pelo denominador da segunda fração e multiplicar
o denominador da primeira fração pelo numerador da segunda fração. Se os resultados obtidos
forem iguais conclui-se que as frações são equivalentes.
Exemplos:
Verifique se cada um dos pares de frações a seguir são equivalentes:
a) 2 e 4 .
4
8
2
4
4
8
2$8 = 4$4
"
16 = 16
Como os resultados foram iguais (16 = 16) temos que as frações são equivalentes.
Logo, 2 + 4 .
4
8
b) 9 e 6 .
12
8
9
12
6
8
9 $ 8 = 6 $ 12
"
72 = 72
Como os resultados foram iguais (72 = 72) temos que as frações são equivalentes.
Logo, 9 + 6 .
12
8
c) 1 e 4 .
2
6
1
2
4
6
1$6 = 2$8
"
6=8
Como os resultados foram diferentes ( 6 ! 8 ) temos que as frações não são equivalentes.
25

26. Matemática
Simplificação de frações
Simplificar uma fração implica em dividir seus termos (numerador e denominador) por um
mesmo número diferente de zero. É importante perceber que haverá situações em que os termos
terão mais de um divisor comum. Por exemplo, a fração 18 onde tanto numerador como o
24
denominador são múltiplos de 2, 3 e 6.
Por conta disso é importante simplificar a fração até que ela fique na sua forma irredutível,
ou seja, até que não seja mais possível encontrar um número que divida seus termos ao mesmo
tempo.
Exemplos:
Simplifique as frações a seguir até sua forma irredutível:
a) 60 ' 2 = 30 ' 3 = 10 ' 5 = 2
90 ' 2
45 ' 3 15 ' 5 3
b)
84 ' 2 = 42 ' 3 = 14 ' 7 = 2
126 ' 2
63 ' 3
21 ' 7 3
Atividades
01 Simplifique cada uma das frações a seguir até torná-las irredutíveis.
a)
54
81
c)
512
600
b)
d)
150
180
125
175
Sugestão de solução:
a) a)
2
5
64
5
; b)
; c)
; d) .
3
6
75
7
02 Verifique quais dos pares de frações são equivalentes:
a)
36
36
e
24
24
c)
100
400
e
125
500
b)
d)
36
50
e
60
70
7
84
e
5
60
Sugestão de solução:
a) não; b) não; c) sim; d) sim.
03 Marque V se a afirmativa for verdadeira e F se a afirmativa for falsa.
a) ( ) A fração
26
30
35
encontra-se em sua forma irredutível.

27. Matemática
b) ( ) As frações
86
56
e
93
63
c) ( ) Se simplificar a fração
são equivalentes.
84
108
por 2 e o resultado obtido por 3, a nova fração será igual a
d) ( ) A forma irredutível da fração
136
140
é igual a
34
35
.
.
7
9
14
18
.
Sugestão de solução:
a) F; b) F; c) V; d) V.
Desafio
Determine três frações equivalentes à forma irredutível
Sugestão de solução:
14 21 35
;
;
18 27 45
AULA 06
Conjunto dos números racionais (Q ) –
Conversão
Objetivo geral
Compreender e transformar fração em números
decimais e vice-versa.
Conceito básico
Em nosso dia a dia nos deparamos com números
escritos na forma de fração e precisamos transformá-los
em números decimais para facilitar a resolução de diversas
situações problema.
Exemplo 1:
Márcio passou R$10,00 para que seus 20 sobrinhos
dividissem em partes iguais. Quanto cada um ganhou?
O que devo aprender
nesta aula
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.
27

28. Matemática
Sugestão de solução:
Total em dinheiro: R$ 10,00
Quantidade de sobrinhos: 20
100
20
100
0, 5
0
Portanto, cada sobrinho ganhará R$ 0,50.
Exemplo 2:
Efetue a divisão e escreva na forma decimal
a)
32 =
125 =
3, 2 b)
1, 25
10
100
c)
5 =
0, 005
1000
e)
5 =
0, 005
1000
d)
28 =
0, 028
1000
Atividades
01 Represente a fração decimal
Sugestão de solução:
1,21
121
100
na forma decimal.
02 Represente cada uma das frações na forma decimal.
a)
2
10
d)
3 148
10
e)
68
100
g)
2 634
100
h)
538
1 000
j)
8 356
1 000
b)
l)
35
10
518
10
c)
448
100
f)
4 761
10 000
i)
5 114
1 000
m)
15 832
10 000
Sugestão de solução:
a) 0,2; b) 3,5; c) 51,8; d) 314,8; e) 0,68; f) 4,48; g) 26,34; h) 0,538; i) 5,114; j) 8,356; l) 0,4761; m) 1,5832.
28

29. Matemática
03 Represente os números decimais em frações:
a) 0,3 =
b) 5,3 =
d) 0,654 =
c) 6,99 =
e) 4,336 =
Sugestão de solução:
a)
3
10
d)
654
1 000
b)
e)
53
10
c)
699
100
4 336
1 000
Desafio
Observe as frações e suas respectivas representações decimais.
I.
3 =
0, 003
1000
II.
2 367 =
23, 67
100
III.
129 =
0, 0129
10 000
IV.
267 =
2, 67
10
Analisando as igualdades apresentadas, escolha a alternativa que expressa as representações corretas.
a) I e II
b) I e IV
c) I, II e III
d) I, II, III e IV
Sugestão de solução
Letra c.
29

30. Matemática
AULA 07
Conjunto dos Números Irracionais
Objetivo Geral
Ampliar os conceitos sobre o conjunto dos números
irracionais bem como suas operações.
O que devo aprender
nesta aula
u Reconhecer que a união dos
Conceito Básico
Os números irracionais são os números que não podem
ser representados pela divisão de dois inteiros; ou seja, são
números reais, mas não são racionais. O conjunto dos
números irracionais é representado por alguns autores
pelo símbolo I .
Sendo assim, representando a ideia expressa ante­ ior­
r
mente em forma de diagrama temos:
números Racionais e Irracionais
constitui o conjunto dos
números Reais.
u Reconhecer um número
irracional.
u Criar e resolver situações
problema que envolve
números irracionais.
Exemplos de números irracionais.
r , { , p , onde p é um número primo.
Observação: a raiz quadrada de qualquer número primo é um número irracional.
Atividades
01 Observe os números escritos no quadro a seguir
30

31. Matemática
4
3600
3
36
17
Quais desses números são racionais e quais são irracionais?
Sugestão de solução
Racionais: 4 = 2 ; 36 = 6 ; 3600 = 60 ;
Irracionais: 3 ; 17 , pois 3 e 17 são primos.
02 O número irracional r está compreendido entre os números:
a) 0 e 1
c) 2 e 3
b) 1 e 2
d) 3 e 4
Sugestão de solução:
d.
03 Considere a expressão: 3
2 -4 2 +
2 -3 3
Qual das alternativas corresponde ao resultado simplificado desta expressão?
a) 0
b) 4 4 - 4 2 - 3 3
c) - 3 3
d) não tem como simplificar esta expressão
Sugestão de solução:
Letra c.
Desafio
Escreva quatro números irracionais que estejam compreendidos entre 1 e 10
Sugestão de solução
Existem infinitos números irracionais entre 1 e 10, como exemplo, podemos citar um número bem famoso:
r , 3, 14 ;
3 ;
5 ;
7 ; e
8.
31

32. Matemática
AULA 08
Conjunto dos Números Reais (R )
Objetivo Geral
Conhecer a definição conceitual de números reais
Conceito Básico
O conjunto dos números reais R é determinado
pela união do conjunto dos números racionais com o
conjunto dos números irracionais.
Como já estudamos nas aulas anteriores:
O que devo aprender
nesta aula
u Reconhecer que a união dos
números Racionais e Irracionais
constitui o conjunto dos números
Reais.
u Identificar cada número real
N " simboliza o conjunto dos Números Naturais
com um ponto da reta e viceversa.
N = "0, 1, 2, 3, 4, 5 ... ,
u Utilizar as propriedades das
Z " simboliza o conjunto dos Números Inteiros
Z = "... , - 3, - 2, - 1, 0, 1, 2, 3... ,
Q " simboliza o conjunto dos Números Racionais
5
3
Q = '... , - 3, - , - 2, - 1, 0, , 1, 2, 3 ... 1
2
5
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
problema que envolvem números
reais ampliando e consolidando
os significados das operações
adição, subtração, multiplicação,
divisão, potenciação e radiciação.
Observação: usaremos o símbolo I para representar o
conjunto dos Números Irracionais
Assim, I é o conjunto formado pelos números que
não podem ser representados na forma de uma fração, ou seja, não podem ser obtidos pela divisão
de dois números inteiros. Então podemos falar que os irracionais são números decimais infinitos
e não periódicos.
Exemplos:
2 , 3 , e r.
R " simboliza o conjunto dos Números Reais
R = Q,I
Representando os conjuntos na forma
de diagrama temos:
32

33. Matemática
Na reta numérica o conjunto dos números reais pode ser representado da seguinte forma:
Quando trabalhamos com operações no campo dos números reais nos retratamos das operações
revisadas anteriormente no conjunto N, Z, I, Q e R .
Veja o seguinte exemplo que retrata operações no campo dos números reais:
Calcule e descubra o valor do resultado das seguintes operações:
a) 3 3 + 2 3 = b)
c)
3 $ 3 = d)
Sugestão de solução
a) 5 3
b) 1
c)
9 =3
d)
18 =
2
0 + 1 =
18 =
2
9 =3
Atividades
01 Seja o conjunto B = "
3 , 13 , 16 ,
25 ,
30 ,
64 , .
a) Quais desses números são naturais?
b) Quais desses números são racionais?
c) Quais desses números são irracionais?
d) Quais desses números são reais?
Sugestão de solução
a) 16 , 25 ,
b)
16 ,
c)
3 , 13 ,
d) 3 ,
reais.
25 ,
64 ,
pois são raízes quadradas exatas.
64 ,
pois todo número natural também é um número racional.
30 ,
13 , 16 ,
são irracionais, pois se trata de raiz quadrada não exata.
25 ,
30 ,
64 ,
todo número racional ou irracional faz parte do conjunto dos números
02 O valor numérico da expressão x2 – 3x + y + 9 para x = 6 e y = 5 indica a idade da professora Rita.
Faça os cálculos e descubra quantos anos a professora Rita tem.
Sugestão de solução
Substituindo os valores de x e y na expressão temos:
33

34. Matemática
x2 – 3x + y + 9 = 62 – 3.6 + 5 + 9 = 36 – 18 + 5 + 9 = 32.
Portanto, a professora Rita tem 32 anos.
03 Indique corretamente a localização dos números reais a seguir na reta númérica:
3
r
-3,4
- 1
5
-3
2
Sugestão de solução
Distribuindo esses números na reta numérica temos:
04 O número
51
é um número pertencente ao conjunto dos números
a) naturais
b) inteiros
c) racionais
d) reais
Sugestão de solução
Como já sabemos o número 51 não possui raiz quadrada exata, logo é um número irracional e todo número
irracional pertence ao conjunto dos números reais. Alternativa d.
Desafio
Determine o que se pede na tabela a seguir:
01 Escreva cinco números naturais ( N )
02 Escreva cinco números inteiros positivos ( Z+)
03 Escreva cinco números inteiros negativos ( Z- )
04 Escreva cinco números Racionais ( Q )
05 Escreva cinco números irracionais ( I )
06 Escreva cinco números Reais ( R )
34

35. Matemática
AULA 09
Os números racionais na reta numérica
Objetivo geral
Possibilitar ao estudante a ampliação sobre o conjunto dos números racionais, relacionandoos com outros conjuntos e representando-os na reta numérica.
Conceito básico
Um número é dito racional quando puder ser escrito na
for­ma fracionária a , sendo a (numerador) e b (denominador)
b
números inteiros e o b ser, obrigatoriamente, diferente de
zero. Sendo assim, o quociente dessa divisão também será
denominado número racional.
Portanto,
O que devo aprender
nesta aula
u Identificar cada número real
com um ponto da reta e viceversa.
 Todo número natural ( N ) é um número racional uma vez que qualquer natural n é escrito
na forma n .
1
3
Ex: 3 = 1 e 15 = 15 .
1
 Todo número inteiro ( Z ) é um número racional uma vez que qualquer inteiro n é escrito
na forma n .
1
-7
- 26
7
Ex: - 7 = 1 =- 1 e - 26 = 1 =- 26 .
1
 Todo número escrito na forma decimal, também, é um número racional, uma vez que todo
número decimal pode ser escrito na forma ` a , com a e b ! Z, com b ! 0j .
b
2
Ex: 1, 8 = 18 e 0, 6 = 3 .
10
O conjunto dos números racionais é formado pelos números racionais positivos e negativos,
juntamente com o zero. Este conjunto é representado pela letra ( Q ), por ser a letra inicial da
palavra quociente.
35

36. Matemática
Atividades
01 A professora Raquel escreveu os seguintes alguns números no quadro, conforme mostra a figura a seguir.
Quais dos números escritos pela professora Raquel são racionais:
a) inteiros?
b) escritos na forma decimal?
c) escritos na forma fracionária?
Sugestão de solução
a) 1, +4, +6 e 12 b) -2,1; 0,11 e +3,5 c) - 1
5
e+
3
5
02 Escreva a quais conjuntos (IN, Z ou Q) pertencem os números:
a) – 6
b) + 8
d) – 5,9
c) + 3
5
Sugestão de solução
a) Z e Q b) IN, Z e Q c) Q d) Q
e) 32
e) IN, Z e Q
03 Observe a reta numérica a seguir e indique:
a) O ponto que corresponde ao número + 3 .
4
b) O número racional que corresponde ao ponto N.
c) O número racional que corresponde ao ponto X.
d) O ponto que corresponde ao número - 1 2 .
4
e) O ponto que corresponde ao número – 3.
Sugestão de solução
a) Z b)
36
7
3
ou 1
4
4
c) - 11
4
3
ou - 2
4
d) T
e) X

37. Matemática
Desafio
Se necessário, troque ideias com seus colegas e complete a tabela com números racionais, substituindo o
símbolo
por números que tornam as igualdades verdadeiras.
Sugestão de solução
AULA 10
Potenciação: Definição
Objetivo geral
Recordar os conceitos de potenciação com expoente
inteiro não negativo e base real diferente de zero.
Conceito básico
a n = a $ a $ a $ ... $ a,
1 44 2 44 3
4
4
n - vezes
a!R e n!Z
a ) base
u Reconhecer a importância das
operações que envolvem números
reais, inclusive potenciação e
radiciação, para a resolução de
problemas dos mais variados
contextos sociais e culturais.
u Utilizar as propriedades das
A potenciação é a operação matemática que envolve o
produto de fatores iguais. Denominaremos por
a n ) potência
O que devo aprender
nesta aula
operações com números reais
como facilitadoras da resolução de
situações problema.
u Criar e resolver situações
n)
expoente.
Numa potenciação, o expoente indica quantas vezes a
base será multiplicada.
problema que envolvem números
reais ampliando e consolidando os
significados das operações adição,
subtração, multiplicação, divisão,
potenciação e radiciação.
37

38. Matemática
Note que o expoente n é um número inteiro. Iremos trabalhar inicialmente com valores
positivos para n.
Exemplo:
Calcular o valor de 54.
5 4 = 5 $ 5 $ 5 $ 5 = 625
Expoente maior que 1.
Vejamos o exemplo:
a) Calcular 25.
2 ) base
5 ) expoente
25 ) potência
2 $ 2 $ 2 $ 2 $ 2 ) fatores
25 = 2 $ 2 $ 2 $ 2 $ 2 = 32
Perceba que o expoente indica quantas vezes a base será multiplicada.
b) Calcular ^- 5h3
^- 5h ) base
3 ) expoente
^- 5h3 ) potência
^- 5h $ ^- 5h $ ^- 5h ) fatores
^- 5h $ ^- 5h $ ^- 5h = - 125
Observação: Professor, lembre-se nesse momento da importância de relembrar as
operações com sinais.
Expoente igual a 1.
Como o expoente indica quantas vezes a base será multiplicada, então se o expoente é igual a
1, a potência será igual à base.
Vejamos os exemplos:
71 = 7
7 ) base
1 ) expoente
71 ) potência
^- 12h1 =- 12
^- 12h ) base
1 ) expoente
^- 12h1 ) potência
Deste modo, podemos afirmar que todo número elevado a é igual ao próprio número.
Expoente igual a 0
Todo número não nulo elevado a zero é igual a 1.
38

39. Matemática
Exemplo: 20 = 1, 30 = 1 e 50 = 1.
Vejamos como isso acontece:
26 = 64
25 = 32
24 = 16
23 = 8
22 = 4
36 = 729
53 = 125
32 = 9
'2
54 = 625
33 = 27
'2
55 = 3 125
34 = 81
'2
56 = 15 625
35 = 243
'2
52 = 25
Observe que quando o expoente é igual a 1, o resultado é a própria base, que pode ser obtido
utilizando a mesma estratégia acima.
21 = 2
31 = 3
51 = 5
Seguindo o processo de divisão, concluímos que todo número não nulo elevado a zero é igual
a 1. Não podemos esquecer que a base tem que ser diferente de zero uma vez que 00 gera uma
indeterminação.
20 = 1
30 = 1
50 = 1
Atividades
01 Calcule as seguintes potências:
a) 24
b) (-3)2
c) (-5)1
d) 70
e) (-12)3
f) ` 3 j2
g)
4
`- 2 j
5
h)
4
5
`- 3 j
10
i) 1,24
j) -(-0,2)2
Sugestão de solução:
a) 16; b) 9; c) -5; d) 1; e) -1 728; f)
9
16
; g)
16
625
; h) -
243
100 000
; i) 1,44 j) -0,04
02 Uma das maneiras de obter a medida da área do quadrado é através da fórmula l2, onde l indica a medida do
seu lado. Nessas condições, qual é a medida da área do quadrado, quando o lado mede
a) 3 cm. b) 2,5 m.
c) 3 km. d) 7 m.
e) 9,3 m.
39

40. Matemática
Sugestão de solução:
a) A = 9 cm2.
d) A = 49 m2.
b) A = 6,25 m2. c) A = 9 km2.
e) A = 86,49 m2.
03 Responda:
a) Se a base tem sinal positivo e expoente par, qual será o sinal da potência?
b) Se a base tem sinal positivo e expoente ímpar, qual será o sinal da potência?
c) Se a base tem sinal negativo e expoente par, qual será o sinal da potência?
d) Se a base tem sinal negativo e expoente ímpar, qual será o sinal da potência?
Sugestão de solução
Base
+
+
–
–
Expoente
Par
Ímpar
Par
Ímpar
Potência
+
+
+
–
Desafio
Márcio fez a seguinte proposta a seu filho Gustavo. Daria R$ 1,00 no primeiro mês e iria dobrando esse
valor a cada mês, enquanto isso Gustavo daria a seu pai R$ 50,00, por mês. Ao final de 9 meses, quem terá
recebido mais dinheiro? Quanto?
Sugestão de solução:
Pagamentos feitos a Gustavo por Márcio
1 mês 2 mês 3 mês 4o mês 5o mês
6o mês
7o mês
8o mês
9o mês
R$ 1,00 R$ 2,00 R$ 4,00 R$ 8,00 R$ 16,00 R$ 32,00 R$ 64,00 R$ 128,00 R$ 256,00
o
o
o
Portanto, Márcio pagou R$ 511,00 para Gustavo.
Pagamentos feitos a Márcio por Gustavo
1 mês 2 mês 3 mês 4o mês 5o mês
6o mês 7o mês
8o mês
R$ 50,00 R$ 50,00 R$ 50,00 R$ 50,00 R$ 50,00 R$ 50,00 R$ 50,00 R$ 50,00
o
o
o
Portanto, Gustavo pagou R$ 450,00 para Márcio.
Logo, Gustavo recebeu mais que Márcio R$ 61,00.
40
9o mês
R$ 50,00

41. Matemática
AULA 11
Potenciação: Propriedades
Objetivo geral
Recordar as propriedades de potenciação com expoente inteiro não negativo e base real
diferente de zero.
Conceito básico
Como podemos resolver 5 $ 5 $ 5 e apresentar o resulta­ o
d
em forma de potência?
3
2
4
O que devo aprender
nesta aula
u Reconhecer a importância
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
Vamos lá.
53 = 5 $ 5 $ 5
52 = 5 $ 5
54 = 5 $ 5 $ 5 $ 5
Sabendo que o expoente indica quantas vezes a base será
multiplicada, então
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
Portanto teremos nove vezes o valor 5, assim 5 $ 5 $ 5 = 5 .
3
2
4
9
1ª propriedade:
Em um produto de potência de mesma base, devemos
conservar a base e somar os expoentes.
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.
Dado a ! R e n, m ! N , então a n $ a m = a n + m .
Observe o seguinte quociente: 5 4 ' 5 2
54 ' 52 =
5$5$5$5
5$5
Simplificando os fatores comuns,
54 ' 52 =
5 $5 $5$5
5 $5
Assim,
54 ' 52 = 54 - 2 = 52
41

42. Matemática
2ª propriedade:
Em uma divisão de potência de mesma base, devemos conservar a base e subtrair os expoentes.
n
Dado a ! R* e n, m ! N , então a n ' a m = a n + m ou am = a n - m .
a
Uma outra situação é apresentada na propriedade a seguir:
Calcule (23)4
^23h4 = 23 $ 23 $ 23 $ 23 = 2 $ 2 $ 2 $ 2 $ 2 $ 2 $ 2 $ 2 $ 2 $ 2 $ 2 $ 2 = 212
SSSS
2
3
2
3
2
3
2
3
Assim, ^23h4 = 23 $ 4 = 212
3ª propriedade:
Em uma potência, onde a base é uma potência, devemos conservar a base e multiplicar os
expoentes.
Dado a ! R* e n, m ! N , então ^a nhm = a n - m .
Exercícios
01 Aplicando as propriedades, escreva o resultado na forma de uma só potência.
a) 95 $ 93 b) ^- 4h2 $ ^- 4h $ ^- 4h3
c) 0, 5 $ 0, 52 $ 0, 53 d) `- 3 j3 $ `- 3 j2 $ `- 3 j5 $ `- 3 j1
5
5
5
5
Sugestão de solução:
a) 98 b) ^- 4h6
c) 0, 56 d) `- 3 j11
5
02 Aplicando as propriedades, escreva o resultado na forma de uma só potência.
a)
3
9 5 b) ^- 3h
2
9
^- 3h2
`- 2 j
7
c)
6
5 d) 10
2 4
10 5
`- j
5
Sugestão de solução:
b) -3
a) 93
42
c) `- 2 j3
5
d) 10

43. Matemática
03 Resolva as seguintes expressões:
a) ^35h2 b) ^42h6 c) ^53h3 d) `` 2 j j
3
6 3
Sugestão de solução:
a) 310
c) 59 d) ` 2 j
3
18
b) 412
Desafio
Simplificando a expressão
;
^0, 0001h4 $ 1027 $ ^0, 01h5
E
6
100 3 $ ^0, 1h
Obtemos como resultado:
a) 10-6
b) 10-3
d) 10
e) 103
c) 10-2
Sugestão de solução:
Alternativa d.
AULA 12
Potência com expoente negativo
Objetivo geral
Recordar os conceitos de potenciação com expoente
inteiro e base real diferente de zero.
O que devo aprender nesta aula
u Reconhecer a importância das
Conceito básico
A professora Marina pediu para que seus alunos
resolvessem o seguinte quociente: 53 ' 5 4 .
Julieth resolveu de duas maneiras e perguntou a
professora qual era a maneira correta.
operações que envolvem números reais,
inclusive potenciação e radiciação, para
a resolução de problemas dos mais
variados contextos sociais e culturais.
u Utilizar as propriedades das
Vejamos suas respostas.
operações com números reais como
facilitadoras da resolução de situações
problema.
1º maneira:
u Criar e resolver situações problema
5 $5 $5
53
=1
5 '5 = 4 =
5
5 $5 $5 $5 5
3
4
2ª maneira:
53 ' 5 4 =
53 = -1
5
54
que envolvem números reais ampliando
e consolidando os significados
das operações adição, subtração,
multiplicação, divisão, potenciação e
radiciação.
43

44. Matemática
A resposta da professora surpreendeu Julieth pois as duas estavam corretas.
No estudo de potências, nos deparamos com expoente negativo. Vejamos como proceder
nesse caso:
23 = 8
22 = 4
21 = 2
20 = 1
2-1 =
1 = -1
2
2
2-2 =
1 = -2
2
2-2
1
2 = -3 = 2-3
2
33 = 27
32 = 9
'2
'2
51 = 5
30 = 1
'2
52 = 25
31 = 3
'2
53 = 125
50 = 1
1
3
5-1 =
1
5
3-2 =
1
32
5-2 =
1
52
3-3 =
1
33
5-3 =
1
53
31 =
'2
'2
-3
Assim quando o expoente é negativo e a base é um número real diferente de zero, então:
a- n =
1 = ` 1 jn
a
an
Exemplo:
1) Calcule cada uma das potências a seguir:
a) 3-3
2 -4
b) c 3 m
c) -^- 4h 2
-2
d) `- 10 j
12
Sugestão de solução:
2
-2
4
2
2 -4
81
1
1
a) 3-3 = 13 = 27 ; b) c 3 m = ` 3 j = 16 ; c) -^- 4h 2 = c- 1 m =- 16 ; d) `- 10 j = `- 12 j = 144
12
10
100
2
4
3
Atividades
01 Calcule as potências a seguir:
a) - 4-2
b) `- 5 j c) 7-3
2
-2
1
d) ` 10 j e) -^0, 3h-5
-5
Sugestão de solução:
a) -
44
1 b) 4
16
25
c)
1
343

45. Matemática
d) 1000 000
e) -`
3 -5 = - 10 5 = - 100 000
j
` j
10
3
243
02 Determine o valor da expressão:
^- 2h-3 - `- 2 j
-3
5
Sugestão de solução:
124
8
03 Calcule o valor de ^5
-1
+ 3 -2h-2
Sugestão de solução:
2 025
196
Desafio
Os círculos a seguir estão empilhados formando um triângulo. Utilizando as propriedades da potenciação,
calcule os valores de x, y e z, sabendo que o produto de cada lado é igual .
Sugestão de solução:
45

46. Matemática
AULA 13
Potenciação: expressões numéricas
Objetivo geral
Trabalhar as propriedades da potenciação com expoente
inteiro e base real diferente de zero em expressões numéricas.
u Reconhecer a importância
Conceito básico
Em muitos casos as operações matemáticas se misturam.
Quando nos deparamos com tais situações devemos tomar
cuidado com a ordem de resolução dessas operações. Assim,
primeiramente levamos em conta a ordem de resolução de
parênteses, colchetes e chaves, respectivamente. Em paralelo,
devemos respeitar a seguinte ordem:
1o resolvemos as potenciações e/ou radiciações;
2o resolvemos as multiplicações e/ou divisões;
3 resolvemos as adições e/ou subtrações.
o
Exemplo: Calcule o valor da expressão numérica:
"5 2 + 6^- 3h5 ' ^- 3h4 @3 + ^10 - 4 2h2 ,
Sugestão de solução:
"25 + 6^- 3h5 - 4 @3 + ^10 - 16h2 ,
"25 + 6^- 3h1 @3 + ^- 6h2 ,
"25 + ^- 3h3 + 36 ,
"25 - 27 + 36 ,
"- 2 + 36 ,
34
Atividades
01 Resolva as expressões numéricas a seguir:
a) 32 - 25 ' 23
b) 28 $ 23 - 53 $ 32
c) ^10-3 $ 105h ' 52
46
O que devo aprender
nesta aula
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.

47. Matemática
Sugestão de solução:
a) 5
b) 923
c) 4
02 Gustavo resolveu corretamente a expressão a seguir
;c
5 2 -1 -2
m E
2 -3
2
Qual foi o resultado encontrado por ele?
a) 1
b) 25
c) 625
d) 1
25
e)
1
625
Sugestão de solução:
Alternativa C.
03 Simplifique a expressão x
a-2
$ x - a + 3 $ x a + 1 $ x 2a - 5
Sugestão de solução:
x 3a - 3
Desafio
Qual é o resultado da expressão E =
-3
4
3
2 +5 '5
32
.
Sugestão de solução:
E=
41
.
72
47

48. Matemática
AULA 14
Decomposição
em fatores primos
O que devo aprender
nesta aula
Objetivo Geral
u Reconhecer a importância
Relembrar como decompor um número natural em
fatores primos.
Conceito Básico
A princípio é válido ressaltar que todo número natural
maior que 1 pode ser escrito como produto de dois ou
mais fatores primos. Por exemplo, o número 50 pode ser
escrito como o produto 2 x 5 x 5.
Assim, para se determinar os fatores primos de um
número natural, maior que 1, uma opção é proceder da
seguinte forma:
I) Divida o número especificado pelo menor número
primo que resulte em uma divisão exata. Escreva o valor
obtido da divisão imediatamente abaixo do número a ser
decomposto.
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.
II) Repita o procedimento adotado no tópico anterior de forma iterativa (repetida) até chegar
ao resultado igual a 1(quociente igual a 1). Assim:
48

49. Matemática
III) Os valores (resultados) encontrados na coluna da direita serão os fatores primos do número
em questão (300).
Assim, o número 300 pode ser escrito como produto dos fatores obtidos:
300 = 2 . 2 . 3 . 5 . 5 = 22 . 3 . 52
Atividades
01 Quais desses números abaixo são divisíveis por 2, 3, 4, 5 ou 6?
a) 116
d) 60
b) 30
e) 210
c) 111
f) 405
Sugestão de solução:
116 (2 e 4); 30 (2, 3, 5 e 6); 111 (3); 60 (2, 3, 4, 5 e 6); 210 (2, 3, 5 e 6); 405 (3 e 5).
02 Determine os fatores primos dos números naturais a seguir:
a) 150
c) 62
b) 93
d) 768
Sugestão de solução:
a) 2 . 3 . 52; b) 3 . 31; c) 2 . 31; d) 28 . 3
03 Qual é o número cuja fatoração é:
a) 2 . 33 . 5 . 7
b) 11 . 13
c) 23 . 5 . 7 . 31
d) 2 . 3 . 5 . 7 . 11
Sugestão de solução:
a) 1 890; b) 143; c) 8 680; d) 2 310.
49

50. Matemática
Desafio
No 8º ano da escola BOA NOTA há 35 alunos, e no 9º ano há 42 alunos. Para realizar uma gincana, os estudantes serão organizados em grupos, todos com o mesmo número de alunos e com a condição de que
não se misturem (estudantes de anos diferentes).
A) Qual é o número máximo de alunos que podem haver em cada grupo?
B) Nesse caso, quantos grupos serão formados em cada ano?
Sugestão de solução:
A) 7
B) 5 e 6 respectivamente
AULA 15
Radiciação: Definição / Extração de raiz
Objetivo Geral
Extrair a raiz de números reais apresentados na forma
de radical.
O que devo aprender
nesta aula
Conceito Básico
u Reconhecer a importância
O termo radiciação define a operação inversa da potenciação. O símbolo utilizado na radiciação é o radix ( ).
Ele possui a seguinte estrutura:
9 512 = 2
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
" radical
512 " radicando
9 " índice
2 " raiz
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
É válido ressaltar que o radical que possui índice igual
a 2 omite tal índice de sua simbologia. Veja:
a)
"
lê-se: raiz quadrada (índice igual a 2);
b)
3
" lê-se: raiz cúbica (índice igual a 3);
c)
4
" lê-se: raiz quarta (índice igual a 4).
50
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.

51. Matemática
Extração de raízes por meio da decomposição em fatores primos.
Para extrair uma raiz por meio da decomposição em fatores primos basta seguir os seguintes
passos:
1º passo: Identifique o índice da raiz solicitada. Veja os exemplos:
2º passo: Faça a decomposição em fatores primos do radicando da raiz solicitada:
3º passo: O índice de cada radical determinará o agrupamento dos fatores obtidos. Portanto,
 Em um radical de índice igual 2 os fatores “iguais” da decomposição deverão ser agrupados
de dois em dois.
 Em um radical de índice igual 3 os fatores “iguais” da decomposição deverão ser agrupados
de três em três
 E assim sucessivamente.
51

52. Matemática
4º passo: Substitua o radicando pelo produto dos fatores agrupados de acordo com o índice do
radical e simplifique aqueles fatores cujo expoente são iguais ao seu respectivo índice. O produto
do resultado obtido será a raiz procurada.
I) 144 = 2 2 $ 2 2 $ 3 2 = 2 2 $ 2 2 $ 3 2 = 2 $ 2 $ 3 = 12
II)
125 = 3 53 = 5
3
III)
4
81 = 4 3 4 = 3
IV)
5
1024 = 5 25 $ 25 = 5 25 $ 5 25 = 2 $ 2 = 4
V)
6
64 = 6 26 = 2
Observação: Os exemplos I e IV apresentam em seus desenvolvimentos o produto de
radicandos. Neste caso há uma propriedade de radiciação que diz que a raiz do produto é igual
ao produto das raízes.
Veja a seguinte situação:
Adão e Adriana receberam de herança dois terrenos, ambos com a mesma medida de área.
Adriana ficou com o terreno que possuía 16 m de largura por 36 de comprimento. Sabendo que o
terreno de Adão possuía dimensões iguais de largura e comprimento (terreno no formato de um
quadrado), determine as dimensões do terreno dele.
Inicialmente será necessário determinarmos a medida da área dos terrenos.
As dimensões do terreno de Adriana (16 m de largura x 36 de comprimento) implica em uma
área de medida igual a 576 m2.
Como o terreno de Adão tem o formato de um quadrado e possui 576 m2, temos que:
x $ x = 576 m2 , onde x corresponde à medida do lado do terreno de Adão. Portanto,
x2 = 576
"
x = 576
576 = 2 2 $ 2 2 $ 2 2 $ 3 2 = 2 $ 2 $ 2 $ 3 = 24
52

53. Matemática
Atividades
01 Determine a solução de cada uma das raízes a seguir utilizando método de extração de raízes por meio da
decomposição de fatores primos:
a) 3 27
b) 4
625
c) 7
1258
d) 3
343
Sugestão de solução
a) 3
27 = 3 3 3 = 3
b) 4
625 = 4 5 4 = 5
c) 7
128 = 7 27 = 2
d) 3
343 = 3 7 3 = 7
02 Encontre o valor de cada uma das expressões numéricas:
a)
169 - 3 216 =
b)
2 4 + 3 2 - 3 10 2 + 5 2 =
c)
36 + 6 729 - 3 64 =
Sugestão de solução
a)
169 - 3 216 = 13 - 6 = 7
b)
2 4 + 3 2 - 3 10 2 + 5 2 =
c)
36 + 6 729 - 3 64 = 6 + 3 - 4 = 5
16 + 9 - 3 100 + 25 =
25 - 3 125 = 5 - 5 = 0
53

54. Matemática
03 Qual o comprimento da aresta de uma caixa que possui todas as suas dimensões iguais e medida de volume
igual a 729 dm3?
Sugestão de solução
Temos que o volume (V) de um paralelepípedo é dado pelo produto de suas três dimensões:
V = altura x comprimento x largura
Como o paralelepípedo em questão em um cubo, suas três dimensões serão todas iguais. Portanto,
V = a $ a $ a = a3
O enunciado do problema diz que o volume desta caixa corresponde a 729 dm3, então,
V = a $ a $ a = a3 = 729 dm3
a3 = 729
a = 3 729
a = 9 dm3
Desafio
Obtenha os valores de A, B, C, D, E e F nos quadros a seguir percebendo as relações expressas pelas setas
direcionais.
Sugestão de solução:
A = 484; B = 31; C = 8; D = 4; E = 10; F = 4 096.
54

55. Matemática
Aula 16
Radiciação (propriedades)
Objetivo geral
Compreender e aplicar as propriedades da radiciação.
Conceito básico
Nesta aula estudaremos as propriedades da radiciação
que são muito importantes não só para o estudo dos
radicais mas também para outros temas da Matemática.
Lembrando,
O que devo aprender
nesta aula
u Reconhecer a importância
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
Ao se trabalhar com radicais surgirão uma série de situações nas quais será necessário a
utilização de algumas propriedades. Vejamos algumas delas:
1ª propriedade: a raiz de índice n de um radicando r de expoente, também, n é o próprio
radicando.
n
r n = r , onde r ! R+ , n ! N e n 2 1
Exemplo:
5
32 = 5 25 = 2
2ª propriedade: a raiz de índice n de um radicando r de expoente m pode ser escrita como
uma potência de expoente fracionário onde a base é o radicando r, o numerador do expoente é o
expoente inicial m e o denominador será o índice n do radical.
n
r m = r n , onde r ! R+ , n, m ! N e n 2 1
m
Exemplo:
5
20
2 20 = 2 5 = 2 4 = 16
55

56. Matemática
3ª propriedade: O radical de outro radical pode ser escrito como um radical único onde o índice
deste é igual ao produto dos índices dos radicais anteriores.
n
m
r = n.m r , onde r ! R+ , n, m ! N e n 2 1 e m 2 1
Exemplo:
3
5 = 2.3 5 = 6 5
4ª propriedade: O radical de um produto de radicandos pode ser escrito como o produto dos
radicais de cada radicando.
n
r $ s = n r $ n s , onde r, s ! R+ , n ! N e n 2 1
Exemplo:
4 $ 25 = 4 $ 25 = 2 $ 5 = 10
5ª propriedade: O radical de um quociente de radicandos pode ser escrito como o quociente
dos radicais de cada radicando.
n
r =
s
n
n
r
*
, onde r ! R+, s ! R+, n ! N e n 2 1
s
Exemplo:
25 = 5
3
9
25 =
9
Importante:
n
0 =0
n
1 =1
n
r =r
Atividades
01 Aplicando as propriedades de radiciação, determine o valor de cada radical:
a) 4
b) 3
8
c) 5
3 125
d)
56
16
49

57. Matemática
Sugestão de solução:
a) 4 16 = 2, sendo que 2 4 = 16
b) 3 8 = 2, sendo que 23 = 8
c) 5 3 125 = 5, sendo que 55 = 3 125
d) 49 = 7
02 Encontre o valor de cada uma das expressões:
a) 100 + 3 64 - 4 16
b) 5 8 256 + 3 5 243 - 625
c) 4 3 125 - 8 64 + 400
Sugestão de solução:
a) 12; b) -6; c) -24
03 Aplique a propriedade adequada para cada questão a seguir:
a) 2 $ 7
b) 5 a $ b
c)
d) 4
e) 8
36
16
4$y
37
Sugestão de solução:
a) 2 $ 7 = 2 $ 7
b) 5 a $ b = 5 a $ 5 b
c)
d) 4
7
e) 3 8
36 =
16
36
= 6
4
16
4 $ y = 8 4y
Desafio
Os números a e b são números reais positivos. Nessas condições simplifique os radicais
calculando em seguida a expressão que representa o produto dos radicais obtidos.
6
a3
e 12 b6 ,
Sugestão de solução:
ab
57

58. Matemática
AULA 17
Radiciação inexata
Objetivo geral
Compreender e extrair a raiz de números reais.
Conceito básico
O que devo aprender
nesta aula
u Criar e resolver situações
Como já estudamos na aula 15, o índice de cada radical
determinará o agrupamento dos fatores obtidos. Quando
não for possível agrupar todos os termos iguais obtidos na
decomposição de acordo com o índice indicado no radical,
temos um caso de radiciação inexata. Por exemplo, a 18 .
problema que envolve
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.
Observe que na fatoração acima obtivemos o produto 2.3²; assim, o número 2 ficou fora do
agrupamento, resultando em 3 2 . Portanto, o número 18 possui raiz inexata, sendo assim um
radical irracional já que a raiz quadrada de todo número primo é irracional.
Veja também os exemplos a seguir:
1. Calcule o valor do radical
Sugestão de solução:
3
3
135
135 = 3 33 $ 5 = 3 3 5
2. Qual o resultado da expressão
Sugestão de solução:
48 + 27 ?
48 + 27 = 2 4 $ 3 + 3 2 $ 3 = 4 3 + 3 3 = 12 3
Atividades
01 Calcule o valor das raízes inexatas, usando a decomposição em fatores.
a) 12
b) 20
c) 45
d) 3 54
e) 288
58

59. Matemática
Sugestão de solução:
a)
12 =
2$2$3 =
b)
20 =
22 $ 5 = 2 5
c)
45 =
32 $ 5 = 3 5
d) 3
54 = 3 2 $ 3 3 = 3 3 2
e)
288 =
22 $ 3 = 2 3
2 2 $ 2 2 $ 3 2 2 = 4 $ 3 2 = 12 2
02 Determine o resultado das expressões numéricas a seguir.
a) 3
24 + 3 81
b)
80 + 20
Sugestão de solução:
a) 3
b)
24 + 3 81 = 3 2 3 $ 3 + 3 3 3 $ 3 = 2 3 3 + 3 3 3 = 5 3 3
80 + 20 =
22 $ 22 $ 5 + 22 $ 5 = 4 5 + 2 5 = 6 5
03 Identifique como racional ou irracional cada um dos números a seguir.
a)
b)
c) 3
30
36
27
Sugestão de solução:
a)
b)
c) 3
irracional
36 racional
27 racional
30
Desafio
Determine a solução da expressão
Sugestão de solução:
3
54 + 3 250
3
128
.
8 2
3 2 +5 2
=
=2
4 2
4 2
59

60. Matemática
AULA 18
Relacionando potências e radicais.
Objetivo geral
Identificar e relacionar a potenciação com sua operação
inversa, a radiciação.
Conceito básico
u Reconhecer a importância
Até o momento já vimos que potenciação e radiciação
são operações inversas. Assim:
 Se 9 2 = 81 , então, 81 = 9 ;
 Se 33 = 27 , então,
3
27 = 3 .
Analisemos, agora, os casos que se seguem:
32 = 9
9 = 32 = 3
"
5 2 = 25
"
25 = 5 2 = 5
7 2 = 49
"
49 = 7 2 = 7
103 = 1 000
63 = 216
210 = 1 024
O que devo aprender
nesta aula
"
3
"
"
3
1 000 = 3 103 = 10
216 = 3 23 $ 33 = 2 $ 3 = 6
10
1 024 = 10 210 = 2
das operações que envolvem
números reais, inclusive
potenciação e radiciação, para
a resolução de problemas dos
mais variados contextos sociais
e culturais.
u Utilizar as propriedades das
operações com números reais
como facilitadoras da resolução
de situações problema.
u Criar e resolver situações
problema que envolvem
números reais ampliando e
consolidando os significados
das operações adição,
subtração, multiplicação,
divisão, potenciação e
radiciação.
Observando cada uma das situações acima descritas surge uma dúvida: é possível indicar uma
raiz sem o uso do radical?
Para isso, basta trocarmos o índice do radical e o expoente do radicando por um expoente
fracionário de modo que o expoente do radicando se transforme em numerador e o índice do
radical em denominador.
60

61. Matemática
É importante ressaltar que no conjunto dos números reais não existem soluções para os radicais
cujo radicando é negativo e o índice é par. Veja as situações que se seguem:
 - 4 não possui raiz real, pois se elevarmos tanto o (-2) quanto o (+2) ao quadrado não
chegaremos ao valor do radicando (-4).
 4 - 81 não possui raiz real, pois se elevarmos tanto o (-3) quanto o (+3) à quarta potência
não chegaremos ao valor do radicando (-81).
Exemplo:
Escreva na forma de potência com expoente fracionário as raízes:
a)
5,
33 ,
4
23 e
3
75
1
5 = 52 .
5 : Note que o expoente do radicando é 1 e o índice da raiz é 2, então
3
b) 33 : Note que o expoente do radicando é 3 e o índice da raiz é 2, então 33 = 3 2
3
c)
4
23 : Note que o expoente do radicando é 3 e o índice da raiz é 4, então
4
23 = 2 4
d)
3
75 : Note que o expoente do radicando é 5 e o índice da raiz é 3, então
3
75 = 7 3
5
Atividades
01 Escreva na forma de potência com expoente fracionário as raízes a seguir:
3 3 b)
a) 5
5 4 c)
7
x7
10
Sugestão de solução:
3
7
a) 3 5 b) 5 7 c) x 10
4
02 Escreva na forma de raiz as seguintes potências com expoente fracionário:
1
2
a) 2 7 b) 3 9
7
c) 5 4
Sugestão de solução:
a) 7
2 b)
03 O valor da expressão
a) 1
d) 4
2
3
125 3 $ 9 2
225
3 2 c)
9
4
57
é
b) 2
e) 5
c) 3
Sugestão de solução:
Alternativa C
61

62. Matemática
Desafio
Determine o valor da expressão
Sugestão de solução:
432
3
2
4
4 6 $ 8 3 ' 27 12
5
3
92
729 2
AULA 19
Resolução de
situações problema
envolvendo
números R
Objetivo geral
Resolver situações problema diversas envolvendo números reais, particularmente a potenciação e
a radiciação.
A maioria da população tem acesso à internet
e dentre os muitos sites visitados o facebook é um
dos líderes. A proliferação de uma notícia nesse site
se alastra facilmente. Imagine que Mateus tenha
100 amigos em sua lista. Agora se cada amigo tiver
mais 100 outros amigos, uma notícia publicada por
Mateus pode ser vista por 10 000 pessoas facilmente.
O que devo aprender nesta aula
u Reconhecer que a união dos
números Racionais e Irracionais
constitui o conjunto dos números Reais.
u Reconhecer a importância das
operações que envolvem números
reais, inclusive potenciação e
radiciação, para a resolução de
problemas dos mais variados contextos
sociais e culturais.
u Utilizar as propriedades das
operações com números reais como
facilitadoras da resolução de situações
problema.
u Criar e resolver situações
problema que envolvem números
reais ampliando e consolidando os
significados das operações adição,
subtração, multiplicação, divisão,
potenciação e radiciação.
Atividades
01 Em uma brincadeira de amigo secreto, Marina resolveu surpreender seu amigo. Comprou 5 caixas e, dentro
de cada caixa colocou 5 pacotes. Em cada pacote colocou 5 cartões. Quantos cartões Marina precisou comprar para
surpreender seu amigo secreto?
Sugestão de solução:
53 = 125
62

63. Matemática
02 Observe as figuras a seguir
Com base nessas figuras, podemos realizar a operação matemática (potenciação) para determinar a quantidade de triângulos em casa estágio, veja o quadro.
ESTÁGIO
QUANTIDADE DE TRIÂNGULOS
1
40 = 1
2
41 = 4
3
42 = 16
Continuando com esse processo, quantos triângulos teremos no estágio 5?
a) 32
b) 64
c) 128
d) 256
e) 512
Sugestão de solução:
Alternativa d.
03 Márcio comprou uma caixa em formato de cubo, conforme a ilustração a seguir
A medida do volume dessa caixa é igual 216 cm3. Determine a medida da sua lado, sabendo que a fórmula da
área do cubo é A = a3, onde a corresponde a medida da aresta do cubo.
Sugestão de solução:
a = 6 cm
63

64. Matemática
Desafio
O colégio MJ passará por reformas. Dentre elas, a quadra de esporte será modificada em 10 ambientes
em forma de quadrado de mesma medida de área.
Sabendo que A1 = 36 m2, determine as dimensões da quadra.
Sugestão de solução:
Aula 20
Exercícios – números Reais
Objetivo geral
Revisar por meio de itens e questões o conteúdo relativo a conjuntos numéricos.
Atividades
01 Identifique a alternativa que corresponde à sequencia crescente dos números 2,83; 2,8; 2,75 e 2,6458.
a) 2,6458; 2,8; 2,75; 2,83.
c) 2,6458; 2,83; 2,75; 2,6458.
b) 2,8; 2,75; 2,83; 2,6458.
d) 2,6458; 2,75; 2,8; 2,83.
Sugestão de solução: Letra d.
02 Identifique na reta numérica, a seguir, os números:
64
3
;
10
5
32 ; 2, 5;
3
; 3;
2
4
256 .

65. Matemática
Sugestão de solução:
03 A solução da expressão
a) 1
50 + 32 - 18
72
b) 2
é igual a:
c) 3
d) 4
Sugestão de solução: Letra a.
04 O número decimal correspondente a fração
a) 7,5
b) 1,4
7
5
c) 5,7
é o:
d) 0,75
Sugestão de solução: Letra b.
05 Carlos comprou os produtos relacionados na tabela a seguir:
Produto
Valor
Arroz (5kg)
R$ 8,90
Feijão (1kg)
R$ 3,35
1 lata de óleo
R$ 2,00
O valor total que Carlos pagou foi de:
a) 14,25
b) 14,35
c) 14,45
d) 14,55
Sugestão de solução: Letra a.
06 Identifique entre os números abaixo o único que não é irracional.
a)
8
c)
121
b)
90
d)
200
07 O resultado correto da expressão
2+
3
3
5
3
Sugestão de solução: Letra c.
a)
55
9
c)
é:
5
d) 11
11
5
b) 1
Sugestão de solução: Letra d.
65

66. Matemática
AULA 21
Rotação de polígonos – Propriedades
Objetivo Geral
Reconhecer a simetria de rotação de um
polígono e perceber quais medidas e propriedades
são preservadas.
O que devo aprender nesta aula
Conceito Básico
de reflexão e de translação e perceber
que em cada uma delas se preservam
medidas e propriedades.
Rotação é o movimento de girar uma figura ou
objeto ao redor de um ponto chamado centro de
rotação. A medida do giro é chamada ângulo de
rotação.
u Identificar as simetrias de rotação,
Exemplos:
1º) Rotação em torno de um ponto que pertence a figura ou forma:
2º) Rotação em torno de um ponto fora da figura ou forma:
66

67. Matemática
Atividades
01 A figura a seguir mostra duas semicircunferências.
a) Em torno de que ponto deve-se fazer a rotação de uma das semicircunferência para obter uma circunferência?
b) A rotação deve ser no sentido horário ou anti-horário?
c) De quantos graus deve ser esta rotação?
Sugestão de solução:
a) B.
b) Em qualquer sentido.
c) 180º
02 Observe a figura a seguir e responda os itens
a) Em qual dos quadrados deve-se fazer uma rotação para se obter um triângulo de lados 3, 4 e 5 unidades?
b) Em qual dos pontos deve-se fazer a rotação para obter o triângulo do item a?
c) Em qual sentido deve-se fazer a rotação (no sentido horário ou anti-horário)?
67

68. Matemática
Sugestão de solução:
a) No quadrado de lado 5.
b) No ponto C.
c) Anti-horário.
03 Observe a figura a seguir:
Qual dos itens abaixo se refere a rotação de 90º em torno do ponto E no sentido horário da figura?
Sugestão de solução:
Letra b.
68

69. Matemática
Desafio
Deseja-se encaixar a peça vermelha na peça branca conforme a figura a seguir
Para que isto aconteça deve-se realizar uma única rotação na peça vermelha em que ponto? É
possível determinar o ângulo de rotação? Qual?
Sugestão de solução:
Deve-se realizar uma rotação no ponto A no sentido anti-horário. Quanto ao ângulo observe o
desenho a seguir
Este ângulo mede 45o, pois se trata da diagonal de um quadrado.
69

70. Matemática
AULA 22
Reflexão de polígonos – Propriedades
Objetivo Geral
Identificar a simetria de reflexão e perceber
quais medidas e propriedades são preservadas.
Conceito Básico
Como exemplo pode-se citar que qualquer
imagem ou forma refletida no espelho é uma
reflexão. A reflexão ocorre através de uma reta
chamada eixo de reflexão.
O que devo aprender nesta aula
u Identificar as simetrias de rotação,
de reflexão e de translação e perceber
que em cada uma delas se preservam
medidas e propriedades.
Exemplos:
Sobre a reflexão é válido destacar as seguintes propriedades:
• A figura original e a sua reflexão são geometricamente iguais.
70

71. Matemática
• Dado um ponto e sua reflexão, os mesmos são equidistantes em relação ao eixo de reflexão a
partir de uma reta que os une perpendicularmente ao eixo de reflexão.
• Um ponto sobre o eixo de reflexão é sua própria reflexão.
Atividades
01 Assinale o item a seguir que representa uma reflexão:
71

72. Matemática
Sugestão de solução:
Letra C
02 Quais das alternativas a seguir não representam uma reflexão? Por quê?
72

73. Matemática
Sugestão de solução:
As alternativas que não representam uma reflexão são:
Letra b) Pois, não satisfaz as seguintes propriedades: A figura original e a sua reflexão são geometricamente
iguais; Um ponto e a sua reflexão estão à mesma distância do eixo de reflexão a partir de uma reta que os
une perpendicularmente ao eixo de reflexão.
Letra d) Pois, não satisfaz a seguinte propriedade: A figura original e a sua reflexão são geometricamente
iguais.
Letra e) Pois, não satisfaz a seguinte propriedade: Um ponto e a sua reflexão estão à mesma distância do eixo
de reflexão a partir de uma reta que os une perpendicularmente ao eixo de reflexão.
03 Observe as figuras a seguir na malha quadriculada:
Represente por meio de desenhos todas as reflexões dessas figuras segundo o eixo especificado.
Sugestão de solução:
73

74. Matemática
Desafio
Represente por meio de desenhos duas reflexões seguidas, sendo uma no sentido do eixo y e
outra, a partir da primeira solução, na direção do eixo x respectivamente.
Sugestão de solução:
74

75. Matemática
AULA 23
Translação de polígonos –
Propriedades
Objetivo Geral
Identificar a simetria de translação e perceber
quais medidas e propriedades são preservadas.
O que devo aprender nesta aula
u Identificar as simetrias de rotação,
Conceito Básico
A translação é o termo usado para “mover”
formas, sendo necessárias duas especificações:
a direção (que pode ser medida em graus) e o
deslocamento (que pode ser medida em alguma
unidade de comprimento: cm, m, km, ...).
de reflexão e de translação e perceber
que em cada uma delas se preservam
medidas e propriedades.
Exemplos:
1o) Translação na horizontal (0º ou 180º):
2o) Translação na vertical (90º ou 270º):
75

76. Matemática
3o) Translação na diagonal (diferente de: 0º, 90º , 180º ou 270º):
Atividades
01 Observe a figura a seguir.
Em quantos centímetros, na vertical, deve-se transladar o retângulo ABCD para que ele fique centralizado no
retângulo EFHG?
Sugestão de solução:
Deve-se transladar o retângulo ABCD em 7cm na vertical.
76

77. Matemática
02 Observe as translações 1, 2 e 3.
a) Existe translação na vertical? Qual?
b) Existe translação na horizontal? Qual?
c) Existe translação na diagonal? Qual?
Sugestão de solução:
Letra a) Sim, a 3
Letra b) Sim, a 1
Letra c) Sim, a 2
03 A figura a seguir representa um telhado, que na sua construção utilizou a propriedade da translação.
77

78. Matemática
a) Qual é a medida da translação AA”?
b) Qual é a medida da translação CC’?
c) Quantas translações foram feitas? Quais?
d) As translações ocorreram em quais sentidos? (vertical, horizontal ou diagonal)
Sugestão de solução:
Letra a) 4 m + 3 m = 7 m
Letra b) 4 m
Letra c) duas: ABC para A’B’C’ para A”B”C”
Letra d) as duas translações ocorreram no sentido horizontal.
Desafio
Observe a figura a seguir
Realize apenas três translações indicando o deslocamento em cm e a direção de cada uma delas
para construir um retângulo. Indique também a largura e o comprimento do retângulo.
Sugestão de solução:
78

79. Matemática
Ficando assim:
As dimensões são: Largura 12cm; Comprimento: 12cm.
AULA 24
Plano Cartesiano Ortogonal
Objetivo Geral
Identificar e representar o plano cartesiano e as coordenadas cartesianas.
Conceito Básico
O plano cartesiano ou espaço cartesiano é um esquema semelhante a uma rede quadriculada (reticulada) necessário para especificar pontos num determinado “espaço” com dimensões. Ele é composto de
duas retas perpendiculares e orientadas, uma horizontal denominada de eixo x ou eixo das abscissas e outra
vertical chamada de eixo y ou eixo das ordenadas. Elas
se interceptam no ponto (0,0), denominado origem
do sistema.
A orientação positiva das retas é representada por
uma seta conforme a figura a seguir.
O que devo aprender
nesta aula
u Construir figuras no plano com
base em informações relevantes,
como: construir pontos dadas suas
coordenadas, construir polígonos
dadas as coordenadas de seus
vértices e circunferência dadas as
coordenadas do centro e a medida
de seu raio etc.
79

80. Matemática
Um ponto no plano cartesiano é definido por meio de dois valores, um para o eixo x e outro
para o eixo y, respectivamente nesta ordem, que são denominados “par ordenado”. Esses valores
correspondem as coordenadas do ponto. Por exemplo, o ponto A apresentado no plano cartesiano
anterior corresponde ao par ordenado x = -2 e y = 3, ou seja, às coordendas A(-2, 3).
Atividades
01 Relacione algumas situações onde utilizamos a orientação de linhas e colunas.
Sugestão de solução:
Localizar uma peça no tabuleiro; localizar uma cidade ou estado em mapas; localizar um endereço na planta
baixa; entre outros.
02 No Teatro Palco Iluminado as poltronas são dispostas conforme a figura a seguir.
Sabendo que o primeiro número do par indica a coluna e o segundo indica a linha, escreva as coordenadas
que indicam a posição das poltronas A, B e C.
80

81. Matemática
Sugestão de solução:
A(4,3); B(1,2) e C(3,5).
03 Observe os pontos A, R, G, M, H e P marcados no mapa de uma cidade.
Encontre as coordenadas em que eles se localizam.
Sugestão de solução:
Ponto A = (-1,1); Ponto R = (2,1); Ponto G = (4,1); Ponto M = (-2,-1); Ponto H = (-3,-3) e Ponto P = (2,-2).
04 Observe o plano cartesiano representado a seguir. Escreva os pares ordenados (x, y) que correspondem aos
pontos: A, B, C, D, E e F:
Sugestão de solução:
A = (1, -2); B = (-2, 1); C = (2, 2); D = (-3, -2); E = (0,0); F = (2, 3).
81

82. Matemática
Desafio
Marque no plano cartesiano os pontos a seguir:
A = (-1 , 2), B = (4 , -2), C = (-1 , -2), D = (1 , 2) e F = (-2 , 0).
Sugestão de solução:
82

83. Matemática
AULA 25
Construção de polígonos no plano
cartesiano
Objetivo Geral
Representar, identificar e construir no plano
cartesiano polígono e circunferência.
O que devo aprender
nesta aula
u Construir figuras no plano com
Conceito Básico
Inicialmente é necessário relembrar um polígono
é uma superfície plana limitada por segmentos de reta
(ou linhas poligonais) fechadas onde cada um de seus
vértices é formado pela sucesão de dois segmentos de
retas seguidos.
base em informações relevantes,
como: construir pontos dadas suas
coordenadas, construir polígonos
dadas as coordenadas de seus
vértices e circunferência dadas as
coordenadas do centro e a medida
de seu raio etc.
O polígono divide o plano em duas regiões: a região interior ao polígono e a região exterior
a ele.
À região interior ao polígono damos o nome de região poligonal.
Os polígonos são classificados de acordo com o número de lados e ângulos, conforme a tabela
a seguir:
Números de lados ou
ângulos
3
4
5
6
7
8
9
10
11
12
15
20
Nome do Polígono
Em função do número de ângulos
Em função do número de lados
Triângulo
Trilátero
Quadrângulo
Quadrilátero
Pentágono
Pentalátero
Hexágono
hexalátero
Heptágono
Heptalátero
Octógono
Octolátero
Eneágono
Enealátero
Decágono
Decalátero
Undecágono
Undecalátero
Dodecágono
Dodecalátero
Pentadecágono
Pentadecalátero
Icoságono
Icosalátero
83

84. Matemática
Atividades
01 Observe alguns polígonos presentes em sua sala de aula e represente-os na malha quadricula a seguir.
Classifique os polígonos construídos quanto ao número de lados e ângulos.
02 Observe o plano cartesiano representado a seguir e escreva as coordenadas dos vértices dos triângulos BCF e
ADE. Desenhe os triângulos.
84

85. Matemática
Sugestão de solução:
Triângulo BCF = (-2 , 1); (2 , 2); (2 , 3)
Triângulo ADE = (1 , -2); (-3 . -2); (0 , 0)
03 Quais são as coordenadas do retângulo ABCD?
Sugestão de solução:
A = (1 , 4); B = (4 , 4); C = (4 , 0); D = (1 , 0).
85

86. Matemática
04 Marque os pontos a seguir no plano cartesiano e depois ligue-os de maneira que formem um único polígono.
A = (-2 , 3), B = (2 , 3), C = (4 , 1), D = (-4 , -1), E = (-4 , -2) F = (4 , -2), G = (2 , -4) e H = (-2 , -4).
Sugestão de solução:
86

87. Matemática
Desafio
Represente no plano cartesiano:
a) uma circunferência de centro A = (1 , 2) e raio 2.
b) um triângulo cujos vértices são: A = (0 , 0), B = (-4 , 2) e C = (3 , 4).
Sugestão de solução:
87

88. Matemática
Aula 26
Exercícios envolvendo polígonos
Objetivo geral
Revisar por meio de itens e questões o conteúdo relativo a polígonos.
Atividades
01 Para determinar a quantidade de diagonais que partem de um único vértice de um polígono devemos utilizar
a fórmula d = n - 3, onde d representa a quantidade de diagonais que partem de um único vértice e n a quantidade
de lados deste polígono.
A quantidade de diagonais que partem do vértice A de um eneágono é igual a:
a) 6
b) 7
c) 8
d) 9
Sugestão de solução: Letra d.
02 Para determinar a quantidade de diagonais de um polígono devemos utilizar a fórmula D =
D representa a quantidade de diagonais e n a quantidade de lados deste polígono.
A quantidade de diagonais de um icoságono corresponde a:
a) 340
b) 170
c) 34
d) 17
Sugestão de solução: Letra b.
03 Observe o polígono a seguir.
88
^ n - 3h $ n
2
, onde

89. Matemática
Quantas diagonais faltam para que sejam traçadas todas as diagonais deste octógono?
a) 5
c) 36
b) 20
d) 40
Sugestão de solução: c.
04 Observe o polígono:
A medida do perímetro 2P deste polígono é igual a:
a) 17,11 cm
b) 17,9 cm
c) 18 cm
d) 18,1 cm
Sugestão de solução: d.
05 Construa no plano cartesiano ortogonal a seguir um pentágono e determine as coordenadas de cada um de
seus vértices.
06 Determine a medida do lado de um hexágono regular cujo perímetro (2P) mede 17,4 cm.
89

90. Matemática
AULA 27
Circunferência e círculo:
Definição e diferenças
Objetivo geral
Compreender os conceitos e os elementos de
circunferência e círculo.
Conceito básico
Uma das principais características que podemos
notar na circunferência sobrecai ao fato dela ser a
única figura plana que pode ser girada em torno de
um ponto (centro) sem modificar sua posição.
Assim, podemos dizer que circunferência é o lugar
geométrico de todos os pontos de um plano que estão
localizados a uma mesma distância r, denominado
raio, de um ponto fixo O, denominado o centro da
circunferência.
O que devo aprender
nesta aula
u Construir figuras no plano com
base em informações relevantes,
como: construir pontos dadas suas
coordenadas, construir polígonos
dadas as coordenadas de seus
vértices e circunferência dadas as
coordenadas do centro e a medida
de seu raio etc.
Círculo é a reunião da circunferência com todos os pontos que estão em seu interior.
90

91. Matemática
Observe a circunferência a seguir
Vamos identificar seus elementos:
Centro
Raios
O
A0 , B0 , E0 e G0
Cordas
Diâmetro
AE , BG , CH e DF
AE e BG
OBS: denominaremos por r o raio da circunferência e por d o seu diâmetro.
INFORMAÇÕES IMPORTANTES
1) o diâmetro é a maior corda de uma circunferência;
2) o diâmetro é igual a duas vezes o raio (d = 2r);
3) a medida do comprimento C de uma circunferência é obtida pela fórmula C = 2rr .
Exemplo:
Identifique os elementos na circunferência a seguir
Quais dos segmentos indicados são cordas?
R: O segmento AB e AC.
Quais dos segmentos indicados são raios?
R: O segmento A0, B0 e C0.
Qual do segmento indicado é diâmetro?
R: O segmento AB.
91

92. Matemática
Atividades
01 Sabendo que a medida do raio de uma circunferência é 8 cm. Responda:
a) Qual a medida do seu diâmetro?
b) Qual a medida do seu comprimento?
Sugestão de solução:
a) d = 2r = 2 $ 8 = 16 cm
b) C = 2rr = 2 $ r $ 8 = 16r cm
02 Observe a figura a seguir
Responda:
a) Qual a medida do seu diâmetro?
b) Qual a medida do seu comprimento?
Sugestão de solução:
a) d = 2r = 2 $ 4 = 8 cm .
b) C = 2rr = 2 $ r $ 4 = 8r cm .
03 As circunferências a seguir tem a mesma medida do raio
92

93. Matemática
Determine:
a) Perímetro do triângulo ABC.
b) Soma das medidas do comprimento das circunferências.
Sugestão de solução:
a) perímetro = 24 cm.
b) Soma dos comprimentos = 24r cm .
Desafio
Sabendo que a medida do lado do quadrado é 10 cm, R é o raio da circunferência C2 e r o raio
de C1.
Determine a medida do comprimento da circunferência C1.
Sugestão de solução:
C = 2rr = 2 $ r $ 2, 5 = 5r
93

94. Matemática
Aula 28
Razão I
Objetivo geral
Compreender e aplicar as relações lógicas das
razões matemáticas em situações problema.
Conceito básico
Em matemática a comparação entre dois números
racionais, através de uma divisão, chama-se razão.
Assim, na razão temos uma divisão ou o quociente
entre dois números racionais a e b, representada por
a:b ou a/b ou a , com b ! 0 .
b
O que devo aprender
nesta aula
u Formular e resolver situações-
problema que envolva a ideia de
fração (parte-todo) e também de
razão e divisão.
Lê-se a para b, ou a está para b.
Exemplo:
3: 5 ou 3/5 ou
3
, lê-se 3 para 5, ou 3 está para 5.
5
Os termos de uma razão recebem nomes específicos: o número a é denominado antecedente e
o número b é denominado consequente.
Exemplo:
3 " antecedente
5 " consequente
Razões inversas
Dizemos que duas razões são inversas quando elas têm o produto igual a 1.
Importante: verifique que nas razões inversas o antecedente de uma é o consequente da outra,
e vice-versa.
Exemplo:
5
5
i) 3 e 3 são razões inversas, pois: 3 $ 3 = 1
5
5
4
4
ii) 7 e 7 são razões inversas, pois: 7 $ 7 = 1
4
4
94

95. Matemática
Razões equivalentes
Dada uma razão entre dois números, obtemos uma razão equivalente multiplicando-se ou
dividindo-se os termos de uma razão por um mesmo número racional (diferente de zero).
Obs.: o símbolo + significa equivalente.
Exemplos:
x2
i) 5 + 10 são razões equivalentes, pois: 5 $$ 2 = 10 ou 5 = 10
6 12
6 2 12
6 12
x2
:3
'
5
5
5
ii) 15 + 3 são razões equivalentes, pois: 15' 3 = 3 ou 15 = 3
9
9
9 3
:3
Exercícios resolvidos
01) Em uma avaliação do Enem com 180 questões, Michael acertou 156. Que razão você
poderia escrever para representar a comparação entre o número de acertos e o total de questões
da avaliação?
Sugestão de solução:
Do enunciado temos que Michael acertou 156 das 180 questões do Enem. Como queremos
a razão entre o número de acertos e o total de questões, basta escrevermos a seguinte razão,
simplificando-a, o máximo possível.
:2
número de acertos
=
número de questões
:2
:3
156 = 78 = 39 = 13
180
90
45
15
:2
:2
:3
Portanto, a razão é 13 .
15
02) Isabelle recortou dois pedaços de cartolina, conforme as figuras a seguir, nas seguintes
medidas:
95

96. Matemática
De acordo, com as figuras, determine qual a razão entre a medida do lado do
e a medida do lado do quadrado
quadrado
.
Sugestão de solução:
Do enunciado com a figura temos as seguintes medidas:
seu lado mede 20 cm e quadrado
quadrado
seu lado mede 30 cm.
Como queremos determinar a razão entre a medida do lado do quadrado
lado do quadrado
e a medida do
, basta escrevermos a seguinte razão, simplificando-a, o máximo possível:
:10
lado do quadrado
lado do quadrado
=
20 = 2
30 3
:10
Portanto, a razão é 2 .
3
03) O time de futebol do Goiás obteve, durante o ano de 2012, 23 vitórias, 9 empates e 6
derrotas. Qual é a razão do número de vitórias para o número total de partidas disputadas?
Sugestão de solução:
Do enunciado temos que o time de futebol do Goiás obteve 23 vitórias, 9 empates e 6 derrotas
no ano de 2012.
Como queremos saber qual é a razão do número de vitórias para o número total de partidas
disputadas, primeiro vamos somar a quantidade de vitórias, empates e derrotas:
23 + 9 + 6 = 38
Então, basta escrevermos a seguinte razão:
número de vitórias
número total de partidas disputadas
= 23 , neste caso não dá para simplificar a razão.
38
Portanto, a razão é 23 .
38
Atividades
01 Marcos Vinícius acertou 16 das 20 questões propostas pela professora em uma atividade na aula de matemática.
a) Que razão você poderia escrever para representar a comparação entre o número de acertos e o total de
questões da atividade?
b) Que razão você poderia escrever para representar a comparação entre o número de erros e o total de questões da atividade?
96

97. Matemática
c) Que razão você poderia escrever para representar a comparação entre o número de acertos e o número de
erros da atividade?
Sugestão de solução:
Do enunciado temos que Marcos Vinícius acertou 16 questões, como a avaliação tinha 20 questões, ele errou
4 questões.
:4
a)
número de acertos
número total de questões
Portanto, a razão é
= 16 = 4
20
5
:4
4.
5
:4
b)
número de erros
número total de questões
= 4 =1
20 5
:4
Portanto, a razão é 1 .
5
:4
c)
número de erros
número de acertos
= 4 = 1
16
4
:4
Portanto, a razão é
1.
4
02 O time de futebol do Flamengo obteve, durante o ano de 2012, 12 vitórias, 14 empates e 12 derrotas. Qual é a
razão do número de vitórias para o número total de partidas disputadas?
Sugestão de solução:
Do enunciado temos que o time de futebol do Flamengo obteve 12 vitórias, 14 empates e 12 derrotas no ano
de 2012.
Como queremos saber qual é a razão do número de vitórias para o número total de partidas disputadas,
primeiro vamos somar a quantidade de vitórias, empates e derrotas:
12 + 14 + 12 = 38
Então, basta escrevermos a seguinte razão, simplificando-a, o máximo possível:
:2
número de vitórias
número total de partidas disputadas
= 12 = 6
38 19
:2
Portanto, a razão é
6
19
.
97

98. Matemática
03 Vanessa desenhou as seguintes figuras:
De acordo, com as figuras, determine qual a razão entre:
e a medida da hipotenusa do triângulo
a) a medida da hipotenusa do triângulo
e a medida da hipotenusa do triângulo
b) a medida da hipotenusa do triângulo
.
.
Sugestão de solução:
Do enunciado temos que Vanessa desenhou dois triângulos onde a medida da hipotenusa do triângulo
de 5cm e a medida da hipotenusa do triângulo
é de 25cm.
é
a) Como queremos determinar a razão entre a medida da hipotenusa do triângulo
e a medida da hipotenusa do triângulo , basta escrevermos a seguinte razão, simplificando-a, o máximo possível:
:5
hipotenusa do triângulo
hipotenusa do triângulo
= 5 =1
25 5
:5
Portanto, a razão é 1 .
5
b) Como queremos determinar a razão entre a medida da hipotenusa do triângulo
e a medida da hipotenusa do triângulo , basta escrevermos a seguinte razão, simplificando-a, o máximo possível:
:5
hipotenusa do triângulo
hipotenusa do triângulo
= 25 = 5 = 5
5
1
:5
Portanto, a razão é 5.
98

99. Matemática
Desafio
(Olimpíada Brasileira de Matemática - OBMEP 2007)
Em uma certa cidade, a razão entre o número de homens e mulheres é
res e crianças é 8 . A razão entre o número de adultos e crianças é:
2
3
e entre o número de mulhe-
1
(A) 5
1
(B)
16
1
(C)
12
1
(D)
40
3
(E)
13
1
Sugestão de solução:
Do enunciado temos:
A razão entre o número de homens e mulheres é
2
h =2
"
3
m 3
.
Ou seja, em cada 2 homens teremos 3 mulheres, 4 homens para 6 mulheres ou mesmo, 16 homens para
24 mulheres.
8
8
A razão entre o número de mulheres e crianças é 1 " m = 1 .
c
Ou seja, em cada 8 mulheres teremos 1 criança, 16 mulheres para 2 crianças ou mesmo, 24 mulheres para
cada 3 crianças .
Se para cada 16 homens temos 24 mulheres e para cada 24 mulheres temos 3 crianças, teremos 16 homens para cada 3 crianças, ou, como pede o desafio, 24 + 16 = 40 adultos para cada 3 crianças
Portanto, a razão entre o número de adultos e crianças é de
40 .
3
99

100. Matemática
Aula 29
Razão II (situações problema
envolvendo razões em porcentagens)
Objetivo geral
Representar e aplicar as razões matemáticas no
estudo das porcentagens através da resolução de
situações problema.
O que devo aprender
nesta aula
u Formular e resolver situações-
Conceito básico
As razões além das formas fracionária e decimal,
também podem ser representadas na forma percentual,
onde se utiliza o símbolo %.
Geralmente, podemos dizer que toda razão na
problema que envolvam a ideia de
fração (parte-todo) e também de
razão e divisão.
forma a , onde b = 100, pode ser representada na forma de porcentagem.
b
Exemplo:
30 =
30% , onde lê-se trinta por cento.
100
Na representação de uma razão a , temos:
b
i) Frações equivalentes:
O conseqüente b é um fator natural de 100.
Exemplo:
x 20
4 = 80 =
80%
5
100
x 20
razão equivalente de
consequente igual a 100
Para descobrir que devo multiplicar por 20, basta dividir 100 por 5.
ii) Forma decimal:
O consequente b não é um fator natural de 100.
Exemplo:
0, 375 $ 100 37, 5
3 =
=
= 37, 5%
0, 375 =
8
100
100
forma decimal de
100
3
8

101. Matemática
Exemplos
01) No final de ano sempre há liquidação nos shopping de Goiânia, onde os descontos variam
muito. Suponha que em determinada loja um produto teve o desconto de 7 mil reais sobre um
preço de 20 mil reais. Quanto por cento equivale esse desconto?
Sugestão de solução:
Do enunciado temos inicialmente, a razão de 7 para 20, ou seja, 7 .
20
Aqui podemos resolver este exercício de duas formas:
i)
Usando frações equivalentes, temos:
x5
7 = 35 =
35%
20 100
x5
Para descobrir que devo multiplicar por 5, basta dividir 100 por 20.
ii) Usando a forma decimal, temos:
0, 35 $ 100
7 =
= 35 = 35%
0, 35 =
20
100
100
Portanto, o desconto de 7 mil reais equivale a 35%.
02) O Brasil tem um total de 8.514.876 km2 de superfície territorial. A região CentroOeste ocupa cerca de 1.606.371.505 km2. A área ocupada pela região Centro-Oeste representa,
aproximadamente, quantos por cento da área total do Brasil?
Sugestão de solução:
Do enunciado temos:
área total do Brasil " 8.514.876 km2
área da região Centro-Oeste " 1.606.371.505 km2
Usando a razão:
número de erros
número total de questões
"
1 606 371505 km2
8 514 876 km2
Aplicando a forma decimal, temos:
0, 182 $ 100
1 606 371505
= 18, 2%
- 0, 182 =
8 514 876
100
Portanto, a área ocupada pela região Centro-Oeste no Brasil representa, aproximadamente
18,2%.
101

102. Matemática
03) Obtive um lucro de R$ 3,00 sobre o preço de um produto vendido a R$ 120,00. Quanto
por cento obtive de lucro?
Sugestão de solução:
Do enunciado temos inicialmente, a razão de 3 para 120, ou seja, 3 .
120
Logo simplificando a razão e aplicando a forma decimal, temos:
0, 025 $ 100 2, 5
1 =
=
= 2, 5%
0, 025 =
40
100
100
Portanto, obtive um de lucro 2,5%.
Atividades
01
Representar na forma de porcentagem as seguintes razões:
a) 6
100
b) 15, 4
100
c) 3
4
d) 7
16
Sugestão de solução:
a)
6 =
6%
100
b)
15, 4
= 15, 4%
100
c) Primeiro faço 100 ' 4 = 25
3 = 3 $ 25 = 75 =
75%
4
4 $ 25 100
d) Primeiro faço 100 ' 16 = 6, 25
7 = 7 $ 6, 25 = 43, 75 =
43, 75%
16 16 $ 6, 25
100
02 Nas férias de verão na praia do Futuro em Fortaleza foram coletados 400 kg de lixo. Desse total, 250 kg eram de materiais plásticos.
A quantidade de materiais plásticos representa quanto por cento do total do lixo recolhido?
Sugestão de solução:
Do enunciado temos:
total de lixo coletado na praia " 400 kg
lixo de material plástico " 250 kg
102

103. Matemática
Usando a razão:
lixo de material plástico
total de lixo coletado na praia
"
250 kg
400 kg
Logo, simplificando a razão e aplicando a forma decimal, temos:
0, 625 $ 100
62, 5
5 =
=
= 62, 5%
0, 625 =
8
100
100
Portanto, quantidade de materiais plásticos representa 62,5% do lixo recolhido.
03 Um livro de literatura tem 80 páginas numeradas de 1 a 80. Neste livro 9 páginas tem numeração cuja soma dos algarismos é igual
a 8. Essa quantidade representa quanto por cento do número total de páginas do livro?
Sugestão de solução:
Do enunciado temos:
número total de páginas do livro " 80
número de páginas cuja soma dos algarismos é 8 " 9
Usando a razão:
número de páginas cuja soma dos algarismos é 8
9
"
80
número total de páginas do livro-------------Logo aplicando a forma decimal, temos:
0, 1125 $ 100 11, 25
9 =
=
= 11, 25%
0, 1125 =
80
100
100
Portanto, número de páginas cuja soma dos algarismos é 8 representa 11,25% do número total de páginas do livro.
Desafio
(Enem 2005)
A escolaridade dos jogadores de futebol nos grandes centros é maior do que se imagina, como mostra a pesquisa a seguir,
realizada com os jogadores profissionais dos quatro principais clubes de futebol do Rio de Janeiro, em 2005.
103

104. Matemática
De acordo com esses dados, o percentual dos jogadores dos quatro clubes que concluíram o Ensino Médio é de aproximadamente:
(A) 14%.
(B) 48%.
(C) 54%.
(D) 60%.
(E) 68%.
Sugestão de solução:
Pelo gráfico de colunas, podemos ver que os jogadores que concluíram o Ensino Médio são aqueles que estão indicados nas
duas últimas colunas (é importante observar que para ingressar no Ensino Superior é necessário concluir o Ensino Médio).
Logo, temos 54 + 14 = 68 jogadores que concluíram o ensino médio.
Utilizando uma regra de três simples e lembrando que foram 112 jogadores pesquisados, temos:
112 " 100%
, onde x representa o percentual de jogadores que concluíram o ensino médio.
68 "
x
112 = 100
18
x
6800
" 112 $ x = 68 $ 100 " x =
112
" 60, 71%.
Portanto, o percentual dos jogadores dos quatro clubes que concluíram o Ensino Médio é de aproximadamente 60%.
Aula 30
Proporção
Objetivo geral
Relembrar os conceitos de proporção.
Conceito básico
Matematicamente, numa proporção é uma
sentença que expressa uma igualdade entre duas
razões.
Assim, dizemos que quatro números racionais a,
b, c e d, diferentes de zero, tomados nessa ordem,
expressam uma proporção quando:
a = c
a: b = c: d ou
b
d
O que devo aprender
nesta aula
u Resolver, analisar e formular
situações problema envolvendo
porcentagem e proporcionalidade.
u Construir estratégias para
resolver situações que envolvem
proporcionalidade.
Lê-se a está para b, assim como c está para d.
Exemplo:
6 : 9 = 12 :18 ou
104
12
, lê-se 6 está para 9, assim como 12 está para 18.
18

105. Matemática
Os números a, b, c e d são denominados termos da proporção, onde a e d são denominados
extremos e b e c são denominados meios.
Exemplo:
extremo
extremos
6 : 9 = 12 : 18
6 = 12
19 18
ou
meios
meio
meio
extremo
Propriedade fundamental das proporções
De modo geral, em toda proporção temos que o produto dos extremos é igual ao produto dos
meios e vice-versa.
produto dos extremos
a = c
) a$d = b$c
b d
produto dos meios
Exemplo:
Verifique se os números 3, 7, 12 e 28 formam, nessa ordem, uma proporção.
Use a propriedade fundamental da proporção.
Sugestão de solução:
Do enunciado temos que os números estão em ordem, assim:
a = 3, b = 7 c = 12 e d = 28
Então podemos escrever a seguinte proporção, aplicando a propriedade fundamental:
3 = 12
a = c
+ a$d = b$c "
+ 3 $ 28 = 7 $ 12 "
7 28
b d
)
produto dos extremos: 3 $ 28 = 84
produto dos meios: 7 $ 12 = 84
Como o produto dos extremos é igual ao produto dos meios, temos uma proporção.
Portanto, os números 3, 7, 12 e 28 formam, nessa ordem, uma proporção.
Exemplos
01) Em uma panificadora, para fazer 600 pães, são gastos 100 kg de farinha. Quantos pães
podem ser feitos com 25 kg de farinha?
Sugestão de solução:
Do enunciado, podemos escrever a seguinte relação:
600
x
-
100 , onde x é a quantidade de pães a serem feitos.
25
105

106. Matemática
Daí, temos a seguinte proporção:
600 = 100
x
25
Aplicando a propriedade fundamental da proporção, temos:
600 $ 25 = x $ 100
100x = 15 000
x=
15 000
100
x = 150
Portanto, podem ser feitos 150 pães.
02) Paula usou 40 laranjas para fazer 26 litros de suco, mas como ainda tem 25 laranjas, quantos
litros de suco aproximadamente ainda poderão serão feitos?
Sugestão de solução:
Do enunciado, podemos escrever a seguinte relação:
40 25 -
26 , onde x é a quantidade de litro de sucos que poderão ser feitos, com as 25 laranjas.
x
Daí, temos a seguinte proporção:
40 = 26
25
x
Aplicando a propriedade fundamental da proporção, temos:
40 $ x = 26 $ 25
40x = 650
x=
650
40
x = 16, 25
Portanto, podem ser feitos aproximadamente 16 litros de suco de laranja.
03) Em um colégio estadual da cidade de Ipameri, para cada 4 moças há 5 rapazes estudando.
Como no colégio há 580 rapazes matriculados, quantos estudantes existem no colégio?
Sugestão de solução:
Do enunciado, podemos escrever a seguinte relação:
4 5 -
106
x
, onde x é a quantidade de moças que estudam no colégio.
580

107. Matemática
Daí, temos a seguinte proporção:
4 = x
5 580
Aplicando a propriedade fundamental da proporção, temos:
4 $ 580 = 5 $ x
5x = 2320
x=
2320
5
x = 464
Logo, no colégio existem 464 moças.
Mas, como queremos saber quantos estudantes existem no colégio, basta somarmos o número
de moças e o de rapazes. Assim, temos:
464 + 580 = 1044
Portanto, existem 1044 estudantes no colégio.
Atividades
01 Sabendo que os números 6, 24, 5e o x formam, nessa ordem, uma proporção, aplicando a propriedade fundamental determine o valor de x.
Sugestão de solução:
Do enunciado temos que os números estão em ordem, assim:
a = 6, b = 24 c = 5 e d = x
Então podemos escrever a seguinte proporção, onde aplicando a propriedade fundamental, temos:
a = c
+ a$d = b$c
b
d
"
6 = 5
24
x
120
" 6 $ x = 24 $ 5 " 6x = 120 " x =
6
" x = 20
Portanto, o valor de x é igual a 20.
02 Em uma determinada empresa uma secretária recebe R$ 200,00 pela construção de 16 relatórios. Se ela construiu no fim do mês 42 relatórios, quanto dinheiro ela recebeu?
Sugestão de solução:
Do enunciado, podemos escrever a seguinte relação:
200
x
-
16
42
, onde x é o valor em dinheiro que a secretária recebeu.
107

108. Matemática
Daí, temos a seguinte proporção:
200 = 16
x
42
Aplicando a propriedade fundamental da proporção, temos:
200 $ 42 = x $ 16
16x = 8400
8400
x=
16
x = 525
Portanto, a secretária recebeu R$ 525,00.
03 Em uma receita de bolo, são necessários 2 ovos para cada 0,5 kg de farinha utilizada. Quantos ovos serão
necessários para 2 kg de farinha?
Sugestão de solução:
Do enunciado, podemos escrever a seguinte relação:
2
x
-
0, 5
2
, onde x é a quantidade de ovos a serem gastos.
Daí, temos a seguinte proporção:
2 = 0, 5
x
2
Aplicando a propriedade fundamental da proporção, temos:
2 $ 2 = x $ 0, 5
(Transformando 0,5 em fração temos 1 )
2
1 =
x 4
2
x = 4$2
x=8
Portanto, serão necessários 8 ovos.
108

109. Matemática
Desafio
(Enem 2011)
Um mecânico de uma equipe de corrida necessita que as seguintes medidas realizadas em um carro
sejam obtidas em metros:
a) distância a entre os eixos dianteiro e traseiro;
b) altura b entre o solo e o encosto do piloto.
Ao optar pelas medidas a e b em metros, obtêm-se, respectivamente,
(A) 0,23 e 0,16.
(B) 2,3 e 1,6.
(C) 23 e 16.
(D) 230 e 160.
(E) 2 300 e 1 600.
Sugestão de solução:
Do enunciado, temos a gravura onde a distância a entre os eixos dianteiro e traseiro é de 2300 mm e
que altura b entre o solo e o encosto do piloto é de 160 cm.
Como queremos o valor das medidas a e b em metros, respectivamente, primeiro vamos transformar
mm e cm em m. Assim, usando a tabela básica das unidades de medidas, temos que:
m dcm cm m
1 0
0 0
Logo, temos que 1 m corresponde a 100 cm e a 1000 mm.
Agora, vamos calcular os valores de a e b em metros.
Então, podemos escrever as seguintes relações:
i)
1000 mm 2300 mm -
1m
a
Daí, temos a seguinte proporção:
1000 = 1
2300
a
109

110. Matemática
Aplicando a propriedade fundamental da proporção, temos:
1000 $ a = 2300 $ 1
1000a = 2300
2300
a=
1000
a = 2, 3
Logo, distância a entre os eixos dianteiro e traseiro é de 2,3 m.
ii)
100 cm
160 cm
-
1m
b
Daí, temos a seguinte proporção:
100 = 1
160
b
Aplicando a propriedade fundamental da proporção, temos:
100 $ b = 160 $ 1
100b = 160
160
b=
100
b = 1, 6
Logo, a altura b, entre o solo e o encosto do piloto, é de 1,6 m.
Portanto, as medidas a e b são, respectivamente, 2,3 m e 1,6 m.
110

111. Matemática
Aula 31
Proporção – Propriedade
Objetivo geral
Aplicar as propriedades das proporções matemáticas na resolução de situações problema.
O que devo aprender
nesta aula
u Resolver, analisar e formular
Conceito básico
Na aula anterior estudamos a propriedade
fundamental das proporções. É uma propriedade
extremamente importante no estudo de proporções,
porém, não é a única. Existem, na matemática, uma
série de situações as quais são necessárias a aplicação
de outros propriedades das proporções. A seguir
vamos analisar duas delas:
situações problema envolvendo
porcentagem e proporcionalidade.
u Construir estratégias para
resolver situações que envolvem
proporcionalidade.
1ª propriedade:
Dizemos que em toda proporção, a soma dos dois primeiros termos está para o primeiro (ou
para o segundo), assim como a soma dos dois últimos está para o terceiro (ou para o quarto).
Matematicamente, temos:
 Soma
a = c
a+b = c+d
a+b = c+d
"
e
b d
a
c
b
d
Demonstração
Prove que:
a = c
a+b = c+d
a+b = c+d
"
e
b d
a
c
b
d
Considere as proporções:
a = c
b d
e
b = d
a c
Adicionando 1 a cada membro obtemos:
a+ = c+
1
1 e
b
d
a+b = c+d
b b d d
b+ = d+
1
1
a
c
b+a = d+c
a a c c
111

112. Matemática
a+b = c+d
b
d
b+a = d+c
a+b = c+d
"
a
c
a
c
 c.q.d
Obs: c.q.d significa como queríamos demonstrar.
2ª propriedade:
Dizemos que em toda proporção, a diferença dos dois primeiros termos está para o primeiro
(ou para o segundo), assim como a diferença dos dois últimos está para o terceiro (ou para o
quarto).
Matematicamente, temos:
 Subtração
a = c
a-b = c-d
a-b = c-d
"
e
b d
a
c
b
d
Demonstração
Prove que:
a = c
a-b = c-d
a-b = c-d
"
e
b d
a
c
b
d
Considere as proporções:
a = c
b = d
e
b d
a c
Subtraindo 1 de cada membro obtemos:
a- = c1
1 e
b
d
b- = d1
1
a
c
a-b = c-d
b b d d
a-b = c-d
b
d
b-a = d-c
a a c c
b-a = d-c
(multiplicando ambos os membros por -1)
a
c
a-b = c-d
a
c
c.q.d
Exemplos
01) Em uma festa, a diferença entre o número de moças e rapazes é 20. Sabendo que a razão
entre o número de moças e rapazes é de 7 para 5, quantas moças e quantos rapazes estão na festa?
Sugestão de solução:
Do enunciado temos:
112

113. Matemática
i) a diferença entre o número de moças e rapazes é 20
ii) a razão entre o número de moças e rapazes é de 7 para 5
Assim, fazendo x = o número de moças e y = o número de rapazes, temos o sistema:
*
x - y = 20
x =7
y 5
4
Como temos uma subtração x - y, então aplicando a 2ª propriedade das proporções, na segunda
equação temos:
x-y 7-5
x =7
=
"
7
y 5
x
(como x - y = 20) "
20 = 2
" 2x = 140 " x = 70
7
x
Logo, substituindo o valor de x na primeira equação temos:
x - y = 20 " 70 - y = 20 " - y =- 20 - 70 " - y =- 50 (- 1) " y = 50
Portanto, estão na festa 70 moças e 50 rapazes.
02) Para pintar uma parede da sala de cor diferente, Ricardo deve misturar tinta branca com
tinta azul, na razão de 5 para 3. Sabendo que ele vai utilizar 24 l dessa mistura, quantos litros de
cada cor de tinta serão necessários?
Sugestão de solução:
Do enunciado temos:
i) a razão entre o número de tinta branca e tinta azul é de 5 para 3
ii) vai ser utilizado 24 l da mistura das tintas " tinta azul + tinta branca = 24 l
Assim, fazendo x = tinta branca e y = tinta azul, temos o sistema:
*
x =5
y 3
x + y = 24
4
Como temos uma soma x + y, então aplicando a 1ª propriedade das proporções, na primeira
equação temos:
x+y 5+3
24 = 8
x =5
=
"
" 8x = 120 " x = 15
(como x + y = 24) "
5
5
y 3
x
x
Logo, substituindo o valor de x na segunda equação temos:
x + y = 24 " 15 + y = 24 " y = 24 - 15 " y = 9
Portanto, serão necessários 15 l de tinta branca e 9 l de tinta azul.
113

114. Matemática
03) A soma da idade de Rogério e de seu filho é 45 anos. Sabendo que a idade do pai está para
a idade do filho, assim como 7 está para 2, qual é a idade do pai e a do filho?
Sugestão de solução:
Do enunciado temos:
i) a idade de Rogério (pai) e de seu filho é 45
ii) a razão entre a idade do pai e do filho é de 7 para 2
Assim, fazendo x = idade do pai e y = idade do filho, temos o sistema:
*
x + y = 45
x =7
y 2
4
Como temos uma subtração x + y, então aplicando a 1ª propriedade das proporções, na segunda
equação temos:
x+y 7+2
45 = 9
x =7
=
"
" 9x = 315 " x = 35
(como x + y = 45) "
7
7
y 2
x
x
Logo, substituindo o valor de x na primeira equação temos:
x + y = 45 " 35 + y = 45 " y = 45 - 35 " y = 10
Portanto, Rogério tem 35 anos e seu filho tem 10 anos.
Atividades
01 Jéssica foi fazer uma laranjada e para isso misturou caldo de laranja com água, na proporção de 2 para 9.
Quantos litros de caldo de laranja e de água serão necessários para fazer 5,5 l de laranjada?
Sugestão de solução:
Do enunciado temos:
i) mistura de caldo de laranja com água, na proporção de 2 para 9
ii) a laranjada vai ter 5,5 l
Assim, fazendo x = caldo de laranja e y = água, temos o sistema:
*
x = 2
y
9
x + y = 5, 5
4
Como temos uma subtração x + y, então aplicando a 1ª propriedade das proporções, na segunda equação
temos:
x = 2
y
9
114
"
x+y 2+9
=
x
2
(como x + y = 5, 5) "
5, 5 11
=
x
2
" 11x = 11 " x = 1

115. Matemática
Logo, substituindo o valor de x na primeira equação temos:
x + y = 5, 5 " 1 + y = 5, 5 " y = 5, 5 - 1 " y = 4, 5
Portanto, serão necessários 1 l de caldo de laranja e 4,5 l de água.
02 A diferença entre a idade de dois irmãos é de 12 anos. Sabendo que a idade do mais velho está para a idade
do mais novo, assim como 5 está para 3. Qual é a idade dos dois irmãos?
Sugestão de solução:
Do enunciado temos:
i) a diferença entre a idade de dois irmãos é de 12 anos
ii) a razão entre a idade do mais velho e a idade do mais novo é de 5 para 3
Assim, fazendo x = idade do irmão mais velho e y = idade do irmão mais novo, temos o sistema:
*
x - y = 12
x = 5
y
3
4
Como temos uma subtração x - y, então aplicando a 2ª propriedade das proporções, na segunda equação
temos:
x = 5
y 3
"
x-y 5-3
=
x
5
12 = 2
(como x - y = 12) "
x
5
" 2x = 60 " x = 30
Logo, substituindo o valor de x na primeira equação temos:
x - y = 12 " 30 - y = 12 " - y = 30 - 12 " - y = - 18 (- 1) " y = 18
Portanto, o irmão mais velho tem 30 anos e o mais novo tem 18 anos.
03 Em um grupo de 300 pessoas. Sabe-se que a razão entre o número de homens e mulheres é de 3 para 2,
quantos homens e quantas mulheres fazem parte desse grupo?
Sugestão de solução:
Do enunciado temos:
iii) um grupo de 300 pessoas (homens + mulheres = 300)
iv) a razão entre o número de homens e mulheres é de 3 para 2
Assim, fazendo x = homens e , temos o sistema:
*
x + y = 300
x = 3
y
2
4
Como temos uma subtração x + y, então aplicando a 1ª propriedade das proporções, na segunda equação
temos:
x = 3
y 2
"
x+y 3+2
=
x
3
(como x + y = 300) "
300 = 5
x
3
" 5x = 900 " x = 180
115

116. Matemática
Logo, substituindo o valor de x na primeira equação temos:
x + y = 300
180 + y = 300 " y = 300 - 180 " y = 120
Portanto, fazem parte desse grupo 180 homens e 120 mulheres.
Desafio
Em um determinado colégio o professor de Matemática desafiou seus alunos a descobrirem as idades
de seus dois filhos, em anos. Para isso, ele deu as seguintes informações:
i) O mais velho tinha x anos e o mais novo tinha y anos.
ii) A razão entre a idade do mais velho e do mais novo é de 5 para 3.
iii) A soma das idades era 16 anos.
Qual a idade de cada filho do professor?
Sugestão de solução:
Do enunciado temos:
i) O mais velho tinha x anos e o mais novo tinha y anos.
ii) A razão entre a idade do filho mais velho e do filho mais novo é de 5 para 3.
iii) a soma das idades é 16 anos.
Assim, x = idade do filho mais velho e y = idade do filho mais novo.
Logo, podemos escrever o sistema:
*
x = 5
y
3
x + y = 16
4
Como temos uma subtração x + y, então aplicando a 1ª propriedade das proporções, na segunda equação temos:
x = 5
y 3
"
x+y 5+3
=
x
3
16 = 8
(como x + y = 16) "
x
5
" 8x = 80 " x = 10
Logo, substituindo o valor de x na primeira equação temos:
x + y = 16 " 10 + y = 16 " y = 16 - 10 " y = 6
Portanto, o filho mais velho do professor tem 10 anos e o mais novo tem 6 anos.
116

117. Matemática
Aula 32
Exercícios envolvendo razão
e proporção
Objetivo geral
Revisar por meio de itens e questões o conteúdo relativo a razão e proporção.
Itens e questões
01 Determine dentre as frações a seguir a única que é uma proporção da fração
a)
78
57
b)
156
171
c)
171
156
d)
156 .
342
26
57
Sugestão de solução: d.
02 A forma irredutível da fração
a)
3
4
c)
2
3
d)
é:
2
7
b)
576
864
3
7
Sugestão de solução: c.
03 Identifique o par de frações que encontra-se em proporção.
a)
16
60
e
10
20
b)
9
60
e
18
80
117

118. Matemática
c)
72
12
e
120
20
d)
18
54
e
20
70
Sugestão de solução: c.
04 Determine a forma irredutível da fração
96 .
120
05 Encontre uma fração que esteja em proporção com
06 Determine o valor de x de forma que as frações
12
28
3
5
e
e que seja uma fração composta por múltiplos de 6.
36
x
estejam em proporção.
Aula 33
Perímetro de polígonos diversos
Objetivo geral
Calcular perímetro de polígonos diversos, despertando no aluno o interesse por geometria.
O que devo aprender
nesta aula
u Determinar o perímetro de
Conceitos Básicos
Polígonos são figuras geométricas formadas por
segmentos de retas e caracterizam-se pelos seguintes
elementos: ângulos, vértices, diagonais e lados.
118
polígonos diversos, como quadrado,
retângulo, losango, paralelogramo,
trapézio e hexágono.

119. Matemática
Seguem alguns polígonos
Quadrado
Retângulo
Paralelogramo
Trapézio
Losango
Hexágono
• Existem diversos outros polígonos que não serão citados no momento mas que são bastante utilizados na
matemática, em outras áreas do conhecimento, no dia-a-dia e na natureza. Portanto, fica como atividade extra
a pesquisa sobre eles.
Perímetro (2P): É a soma das medidas de todos os lados de um polígono.
Veja o exemplo: A figura a seguir apresenta um retângulo (dimensões 30m e 40 m) e um
quadrado (lado 20 m).
Observando os dados responda:
119

120. Matemática
a) O perímetro de retângulo e do quadrado.
b) O perímetro total da figura.
Sugestão de solução
a) Retângulo: P = 40 + 40 + 30 + 30 = 140 m e Quadrado: P = 20 + 20 + 20 + 20 = 80 m
b) P total = P (retângulo) + P (quadrado) = 140 + 80 = 220 m.
Atividades
01 O lado de cada quadradinho da malha abaixo mede 1 cm.
De acordo com a figura analise as afirmações:
I – O perímetro da figura I é 12 cm.
II – O perímetro da figura II é 12 cm.
III – O perímetro da figura III é 16 cm.
IV – O perímetro da figura IV é 14 cm.
Quais das afirmações acima são verdadeiras?
a) I, II e III.
b) I, III e IV
c) II, III e IV
d) Todas estão corretas.
Sugestão de solução
Alternativa correta = b
Justificando as demais alternativas
Estão corretas as alternativas I, III e IV. A afirmativa II está incorreta, pois o perímetro da figura II é 14 cm.
120

121. Matemática
02 Observe a figura a seguir:
Determine:
a) O perímetro do retângulo maior considerando os pontilhados.
b) O perímetro da região em destaque, formada pela união dos pontos.
Sugestão de solução
a) Basta calcular o perímetro do retângulo de dimensões 9 cm e 5cm.
P = 9 + 9 + 5 + 5 = 28 cm
b) Perímetro da região em destaque.
P = 22 cm
03 Apresentamos a seguir dois polígonos:
Figura 01
Figura 02
De acordo com as figuras é correto afirmar que
a) O perímetro da figura 01 é 12,2cm e o perímetro da figura 02 é 17,3cm.
b) O perímetro da figura 02 em relação à figura 01 teve um acréscimo de 60%.
c) A diferença do perímetro da figura 02 para figura 01 é de 6,1cm.
Sugestão de solução
Alternativa correta = c
121

122. Matemática
Justificando as demais alternativas
a) Perímetro da figura 01 = 12,2cm
b) Figura 02 teve acréscimo de 50%.
Perímetro da figura 02 = 18,3cm
Desafio
Um milionário construiu sua casa em um condomínio de luxo. Ele deseja cercar o lote em que construiu
sua mansão.
Fonte: Disponível em: <http://www.escolakids.com/perimetro-de-um-poligono.htm/>. Acesso em: 12 de dez. 2012.
Observando a vista panorâmica do lote calcule:
a) Quantos metros de cerca ele deverá fazer considerando as dimensões da figura?
b) Quantos metros de cerca ele deverá fazer se aumentar em cada dimensão da casa 2 metros?
Sugestão de solução
a) P = 13 + 10 + 97 + 50 + 100 + 30 + 10 + 10 = 320m
b) P = (13 + 2) + (10 + 2) + (97 + 2) + (50 + 2) + (100 + 2) + (30 + 2) + (10 +2) + (10 +2) = 336m
122

123. Matemática
AULA 34
Área de polígonos: quadrados
e retângulos
Objetivo geral
Reconhecer e calcular áreas de quadrados e
retângulos.
Conceitos básicos
Retângulos são quadriláteros que possuem
somente ângulos retos. Desta forma, o quadrado
também é considerado um retângulo pois, também,
possui todos os seus ângulos retos. A diferença entre
o quadrado e retângulo, portanto, se dá por conta do
quadrado possuir todos os seus lados iguais.
O que devo aprender
nesta aula
u Compreender e utilizar as fórmulas
de área de figuras planas como
triângulo, losango, paralelogramo,
trapézio, retângulo, hexágono etc. e
de área de superfície de figuras não
planas como o cubo, o cilindro, e o
paralelepípedo.
Para calcular a área de um retângulo basta multiplicar a sua base (b) por sua altura:
A=b.h
Para calcular a área de um quadrado também usamos base x altura, mas, como no quadrado
a base e a altura tem o mesmo tamanho, podemos usar lado x lado, ou ainda, lado ao quadrado.
A = l2
Exemplo:
Vamos calcular a área da figura a seguir:
123

124. Matemática
Esta figura é formada pela junção de um quadrado e um retângulo, portanto, devemos calcular
a área de ambos separadamente e, em seguida, somá-las.
Área do quadrado: A = l2
A = 52 = 25 cm2
Área do retângulo: A = b . h = 5 . 10 = 50 cm2
Então ATotal = AQuadrado +ARetângulo = 25 + 50 = 75 cm2
Atividades
01 Determine a área da região azul na figura a seguir.
O lado do quadrado vermelho mede 4cm.
Sugestão de solução:
A área do quadrado maior é A = 2 8 $ 2 8 = 4 $ 8 = 32 cm2
A área do quadrado menor (vermelho) é A = 4 $ 4 = 16 cm2
Logo, a área azul será 32 - 16 = 16 cm2
124

125. Matemática
02 Observe a figura a seguir
Sabendo que os retângulos B e C possuem as mesmas dimensões, qual a área da região A?
Sugestão de solução:
Aregião_A = 15 . 7 – 2 . 5 . 5 = 105 - 50 = 55 m2
03 O lado de um quadrado mede 10 cm. Se aumentarmos em 50% a medida dos seus lados, qual a medida da
área do novo quadrado?
Sugestão de solução:
A = 15 . 15 = 225 cm2
Desafio
As flores de Geometrix têm formatos muito interessantes. Algumas delas possuem a forma mostrada na
figura abaixo na qual há seis quadrados e doze triângulos equiláteros.
Uma abelha pousou no ponto destacado e andou sobre a borda da flor no sentido horário até voltar ao
ponto inicial. Sabendo que a região cinza tem 24 cm² de área, qual é a distância percorrida pela abelha?
Sugestão de solução:
A área destacada corresponde à soma das áreas de seis quadrados. Portanto, cada quadrado possui 4 cm²
de área e lado 2 cm.
Os lados dos quadrados e dos triângulos equiláteros são todos iguais. Uma volta completa da abelha em
torno da flor corresponde a 24 vezes o lado do quadrado, ou seja, 48 cm.
125

126. Matemática
Aula 35
Área de polígonos – Triângulos
Objetivo geral
Compreender a ideia e calcular a área de triângulos.
Conceito básico
O foco desta aula será o cálculo da área de um
triângulo. O triângulo, como todos sabem é uma
forma geométrica de extrema importância em nossa
sociedade por conta de suas diversas aplicabilidades
do dia-a-dia. Discuta com o professor sobre as
aplicabilidades do triângulo.
A ideia do cálculo da área de uma região triangular
surge do retângulo, uma vez que, a diagonal de um
retângulo sempre divide o mesmo em dois triângulos.
O que devo aprender
nesta aula
u Compreender e utilizar as fórmulas
de área de figuras planas como
triângulo, losango, paralelogramo,
trapézio, retângulo, hexágono etc. e
de área de superfície de figuras não
planas como o cubo, o cilindro, e o
paralelepípedo.
Observe:
Observe as figuras a seguir
Note que em qualquer uma das figuras a área do triângulo ABC é igual à metade da área do
retângulo
126

127. Matemática
Assim, de modo geral, temos que:
ÁREA DO TRIÂNGULO = b $ h
2
Onde: b = medida da base do segmento AB;
h = medida da altura relativa ao lado do segmento AB.
Por exemplo: Observe os triângulos a seguir:
Para determinarmos a área do triângulo ( I ) devemos fazer:
b $ h = 13 $ 9 =
AI =
58, 5 cm2
2
2
Já a área do triângulo ( II) será calculada da seguinte maneira:
b $ h = 12 $ 9 =
AII =
54 cm2
2
2
Uma outra maneira de se calcular a área de um triângulo qualquer desde que sejam conhecidas
as medidas de seus lados a, b e c é pela fórmula:
A=
p $ ^ p - ah $ ^ p - bh $ ^ p - ch
+b+
sendo p = a 3 c o semiperímetro do triângulo
a, b, c " as medidas dos lados do triângulo
127

128. Matemática
Esta fórmula é conhecida como fórmula de Heron.
Assim sendo, observe o triângulo abaixo:
Temos que a medida do perímetro (2P) deste triângulo será:
2P = 13 cm + 14 cm + 17 cm = 44 cm
Portanto, o semiperímetro (P) terá a medida igual a
P=
2P = 44 =
22 cm " P = 22 cm
2
2
Pela fórmula de Heron A =
A=
p $ ^ p - ah $ ^ p - bh $ ^ p - ch , então
p $ ^ p - ah $ ^ p - bh $ ^ p - ch = 22 $ ^22 - 13h $ ^22 - 14h $ ^22 - 15h = 22 $ 9 $ 8 $ 7 = 11 088 cm2
Atividades
01
Observe os triângulos a seguir e descubra o valor de suas respectivas áreas.
Sugestão de solução
a) Aplicando a fórmula da área de triângulo, temos:
b$h
A=
2
"
6 $ 6 = 36 =
A=
18 .
2
2
Logo, a área do triângulo é 18 cm2.
b) Aplicando a fórmula da área de triângulo, temos:
b$h
A=
2
128
"
A=
12 $ 10, 5 126
=
= 63 cm2
2
2

129. Matemática
c) Aplicando a fórmula da área de triângulo, temos:
b$h
A=
2
"
A=
8, 8 $ 6, 6 58, 08
=
= 29, 04 cm2
2
2
Logo, a área do pedaço de madeira é 38,5 cm2.
02
Um pequeno pedaço de madeira tem a forma e as medidas indicadas na figura. Qual é a área desse pedaço de madeira?
Sugestão de solução:
Aplicando a fórmula da área de triângulo, temos:
b$h
A=
2
"
A=
14 $ 5, 5 77
=
= 38, 5 cm2
2
2
Logo, a área do pedaço de madeira é 38,5 cm2.
03
Aplicando a fórmula de Heron descubra o valor da área do triângulo cujos lados medem: 30 cm, 20 cm e 14 cm.
Sugestão de solução
Aplicando a fórmula de Heron temos:
a + b + c = 30 + 20 + 14 = 64 =
p=
32 cm2
2
2
2
A=
p $ ^ p - ah $ ^ p - bh $ ^ p - ch
A=
30 $ ^32 - 30h $ ^32 - 20h $ ^32 - 14h
A=
30 $ ^ 2 h $ ^12h $ ^18h
A = 12 960
A , 113, 84 cm2
de área
129

130. Matemática
Desafio
Um quadrilátero de papel foi recortado de acordo com a figura e as medidas nela indicadas. Sabendo que
as medidas estão em centímetros, determine a área da região A1+ A2.
Sugestão de solução
Aplicando a fórmula da área de triângulo,vamos calcular o valor da área da metade da figura que exatamente igual a A1 + A2:
b $ h = 100 $ 60 = 6000 =
A=
3 000 cm2
2
2
2
14 $ 5, 5 77
=
= 38, 5 cm2
2
2
Logo, A1 + A2 = 3 000 cm2 de área.
130

131. Matemática
AULA 36
Área de polígonos: paralelogramo
Objetivo geral
Reconhecer e calcular a área do paralelogramo.
O que devo aprender
nesta aula
Conceitos básicos
u Compreender e utilizar as fórmulas
Um paralelogramo é um quadrilátero cujos lados
opostos são iguais e paralelos.
de área de figuras planas como
triângulo, losango, paralelogramo,
trapézio, retângulo, hexágono etc. e
de área de superfície de figuras não
planas como o cubo, o cilindro, e o
paralelepípedo.
O paralelogramo possui as seguintes propriedades:
• Ângulos opostos iguais.
• Possui simetria rotacional.
• A diagonal divide o paralelogramo em dois triângulos congruentes.
• Os lados opostos e seus ângulos opostos são iguais.
• Os ângulos de mesmo lado são suplementares.
• As diagonais são suas próprias bissetrizes.
131

132. Matemática
Área de um paralelogramo
A área de um paralelogramo será determinada pelo produto da medida de sua base pela medida
de sua altura.
Exemplo:
A=b.h
Atividades
01 Seja um paralelogramo com as medidas da base e da altura respectivamente, indicadas por 15 cm e 5 cm.
Se construirmos outro paralelogramo que tenha o dobro das medidas da base e altura do outro paralelogramo, qual
será a diferença entre as áreas dos mesmos?
Sugestão de solução:
O primeiro paralelogramo
A = 15.5 = 75 cm²
O novo paralelogramo terá 30 cm de base e 10 de altura.
Então A = 30. 10 = 300cm²
A diferença será 300 – 75 = 225 cm²
02 Na figura abaixo PS mede 33 cm, PQ mede 5 cm, a área do triângulo 1 mede 25 cm² e a área do triângulo 3
mede 7,5 cm². Calcule a área do paralelogramo 4.
Sugestão de solução:
O triângulo 1 temos A = 25c m² e altura = 5cm
132

133. Matemática
Como área do triângulo é
Temos:
base # altura
2
b$5 =
25
2
5 $ b = 50
b = 10 cm
No triângulo 3 temos A = 7,5 cm2 e altura = 5 cm
Então,
b$5 =
7, 5
2
5 $ b = 15
b = 3 cm
Como PS = 33 cm, a base do paralelogramo 4 será:
33 – 3 – 10 =2 0 cm
Área do paralelogramo
A = b . a = 20 . 5 = 100 cm2
03 No plano coordenado, os vértices de um paralelogramo são os pontos A = (-3, -2), B = (6, -2), C = (10, 3) e D =
(1, 3). Determinar a área do paralelogramo ABCD.
Sugestão de solução:
Seja AB a base do paralelogramo e h sua altura, então, AB = 6 - (-3) = 9
h = 3 - (-2) = 5
A Área do Paralelogramo é a base vezes a altura, então,
A = 9 . 5 = 45 unidades de área.
133

134. Matemática
Desafio
(UERJ- 2010) Um terreno retangular tem 800 m de perímetro e será dividido pelos segmentos PA e CQ em
três partes, como mostra a figura.
Admita que os segmentos de reta PA e CQ estão contidos nas bissetrizes de dois ângulos retos do terreno
e que a área do paralelogramo PAQC tem medida S.
Determine o maior valor, em m2, que S pode assumir.
Sugestão de solução:
y será a base e x a altura do paralelogramo.
Através da figura vamos montar um sistema para encontra o valor de x e y.
4x + 2y = 800
2x + y = 400
y = 400 - 2x
SPAQC = xy = ^400 - 2xh x = 400x - 2x2
Logo, S máxima é o ponto máximo da parábola, que é o y do vértice
- D -^ b2 - 4ach - 160000
= 20.000 m2
=
=
-8
4a
4a
134

135. Matemática
AULA 37
Área de polígonos: trapézio
Objetivo geral
Reconhecer e calcular a área do trapézio.
O que devo aprender
nesta aula
Conceitos básicos
O trapézio é um quadrilátero com dois lados
paralelos, chamados de base maior e base menor.
Para calcular sua área temos que somar as duas bases,
dividir por dois e multiplicar o resultado pela altura.
Exemplos:
A=
A=
u Compreender e utilizar as fórmulas
de área de figuras planas como
triângulo, losango, paralelogramo,
trapézio, retângulo, hexágono etc. e
de área de superfície de figuras não
planas como o cubo, o cilindro, e o
paralelepípedo.
^ Base menor + Base maior h $ Altura
2
^ B + bh $ h
2
Observe o trapézio a seguir:
Neste trapézio a altura será 30 m e as bases 50 m e 20 m. Sendo assim:
A=
^50 + 20h $ 30
2
70 $ 30
A=
2
A = 1050 m2
135

136. Matemática
Obs.: Existem tipos diferentes de trapézio, como por exemplo, o trapézio retângulo que possui
um ângulo reto e o trapézio isósceles que tem dois lados iguais.
Atividades
01 No banheiro do colégio BOA NOTA será colocado um espelho com a forma e dimensões da figura abaixo. Precisa
calcular a área do espelho para saber quanto ele custará. Então, qual é a área deste espelho?
Sugestão de solução:
Base menor = 2,8 dm
Base maior = 1,4 + 1,4 + 2,8 = 5,6 dm
Altura = 2,8 dm
A=
^2, 8 + 5, 6h $ 2, 8
2
8, 4 $ 2, 8
A=
2
A = 11, 76 dm2
02 A piscina de um clube em caldas novas tem um formato de um trapézio. A professora Ana levou seus alunos
para um passeio neste clube e chegando lá pediu a eles que calculassem a área desta piscina. A administração do clube
informou a eles as medidas necessárias. Observe o desenho a seguir e calcule sua área.
136

137. Matemática
Sugestão de solução:
A=
^16 + 6h $ 8
2
= 88 m2
03 Com o excesso de chuvas na estrada entre Goiânia e Nerópolis surgiu um buraco que precisa ser pavimentado.
A área deste buraco é igual a 384 cm2. Para chegar a este cálculo foi necessário saber as dimensões do buraco. Observe
o desenho abaixo e calcule a base maior, a base menor e a altura.
Sugestão de solução:
A=
^ 2x + x h $ 2x
2
"
3x $ 2x = 2
A=
3x
2
Então:
3x2 = 384
Base menor = 8 2 cm
x = 128
Base maior = 2 $ 8 2 cm = 16 2 cm
x = 8 2 cm
Altura = 16 2 cm
2
Desafio
A área cinza do gráfico a seguir, representa a distância percorrida por uma pessoa em uma pista de corrida.
Qual foi a distância que essa pessoa percorreu, no intervalo entre 0 e 10 segundos?
Sugestão de solução:
Base menor = 2; Base maior = 4; Altura = 10.
A=
^4 + 2h $ 10
2
= 60 = 30 m
2
137

138. Matemática
AULA 38
Área de polígonos: pentágono
e hexágono
Objetivo geral
Reconhecer e calcular a área do pentágono e do
hexágono.
O que devo aprender
nesta aula
Conceitos básicos
u Compreender e utilizar as fórmulas
de área de figuras planas como
triângulo, losango, paralelogramo,
trapézio, retângulo, hexágono etc. e
de área de superfície de figuras não
planas como o cubo, o cilindro, e o
paralelepípedo.
• Hexágono regular:
Para calcular área de um hexágono regular basta
dividi-lo em seis triângulos equiláteros iguais. Desta
forma, calculamos a área de um triângulo e depois a
multiplicamos por seis. Para isto utilizamos a seguinte
fórmula:
2
Átriângulo equilátero = ^a 3 h
4
Áhexágono regular = 6 $ ^a
2
4
3h
2
Áhexágono regular = ^3 $ a 3 h
2
• Hexágono irregular:
Para calcular a área de um hexágono não regular, dividimos o mesmo em figuras conhecidas
como triângulos, trapézios, retângulos etc. Veja como no exemplo a seguir:
138

139. Matemática
Dividimos a figura em duas novas figuras: um retângulo de área = 11 . 4 = 44 m2 e um trapézio
de área = ^11 + 7h $ 2 = 18 m2
2
Para calcular a área do pentágono, podemos dividi-lo de forma a obter duas novas figuras, que
podem ser: um triângulo e um trapézio.
Observe o exemplo a seguir:
Desta forma, basta calcularmos as duas novas áreas e adicionar os resultados.
Atividades
01 Na figura a seguir está representado um hexágono regular no plano cartesiano. Qual é o valor da sua área?
Sugestão de solução:
Como o hexágono é regular, o ponto B terá como coordenadas (-1, 2), logo AB = 4A.
Este valor é do lado do triângulo ABO.
Logo:
A=
L2
3 $3
42 3 $ 3
=
= 8 3 $ 3 = 24 3 u.a
2
2
139

140. Matemática
02 Em uma cidade no interior de Goiás o prefeito está construindo um bonito jardim em um formato hexagonal.
Observe seu desenho abaixo:
No entanto esse jardim precisa ser gramado e o prefeito quer saber quantos metros quadrados de grama terá
que comprar. Qual é a área do jardim?
Sugestão de solução:
Como este hexágono é irregular, vamos dividi-lo da seguinte forma:
A Área 1 é de um retângulo
A1 = b $ h
A1 = 24 $ 12 = 288 m2
A Área 2 é de um trapézio
A2 =
A2 =
^ B + bh $ h
2
^16 + 6h $ 8
2
= 22 $ 8 = 88 m2
2
A Área 3 é de um triângulo
A3 =
A3 =
140
^ b $ hh
2
^12 $ 10h
2
= 60 m2

141. Matemática
Logo a área total será: 288 + 88 + 60 = 436 m2
Assim, o Prefeito terá que comprar 436 m2 de grama.
03 Calcule a área do pentágono a seguir, sabendo que o lado de cada quadradinho mede 1 cm.
Sugestão de solução:
Nesta figura temos 4 quadradinhos inteiros e 6 quadradinhos pela metade, se juntarmos os 6 quadrados
“metade” teremos 3 quadrados inteiros. Assim teremos: 3 + 4 = 7 quadradinhos inteiros.
Se o lado do quadrado mede 1cm, sua área será 1cm² (lado2).
Então o pentágono tem:
7 .1 cm² = 7 cm² de área.
Desafio
Laura tem um colar feito em couro, com peças cortadas em formato hexagonal regular, como mostra a
figura abaixo. O comprimento do colar é de 70 cm. Laura quer cobri-lo com tecido. Quantos centímetros
quadrados de tecido ela vai utilizar para cobrir o colar todo?
Sugestão de solução:
Vamos dividir o hexágono em 6 triângulos iguais e equiláteros, chamando seu lado de L.
Então, teremos: 70 = 14 L
L = 5 cm
A área de cada hexágono será:
A=
52
3 $3
= 37, 5 3 cm2
2
Como o colar tem 13 hexágonos, sua área será: A = 37, 5
Portanto, Laura vai utilizar 487, 5 3 cm2 de tecido.
3 cm2 $ 13 = 487, 5 3 cm2
141

142. Matemática
AULA 39
Área de superfície de figuras não
planas: cubo, cilindro e paralelepípedo
Objetivo geral
Reconhecer o cubo, o cilindro e o paralelepípedo
entre as figuras geométricas não planas e calcular suas
respectivas áreas, podendo essas encontrarem-se em
situações contextualizadas.
Conceitos básicos
O cubo, o paralelepípedo e o cilindro, são figuras
não planas ou espaciais chamadas de poliedros e
corpos redondos (cilindros). Estes possuem três
dimensões: altura, largura e comprimento.
O que devo aprender
nesta aula
u Compreender e utilizar as fórmulas
de área de figuras planas como
triângulo, losango, paralelogramo,
trapézio, retângulo, hexágono etc. e
de área de superfície de figuras não
planas como o cubo, o cilindro, e o
paralelepípedo.
O Cubo
Para calcular a área da superfície do cubo vamos planifica-lo:
À esquerda temos a imagem do cubo. Ele é formado por seis quadrados iguais. À direita temos
sua planificação, isto é, se abrimos o cubo, ele terá esta forma.
Para calcularmos sua área, basta calcular a área de um dos quadrados que compõem sua
planificação e depois multiplicá-la por seis.
A área do quadrado é Lado², mas o lado deste quadrado, no cubo, é chamado de aresta. Desta
forma, a área da superfície de um cubo é:
Acubo = 6 . Áquadrado = 6.a²
Por exemplo, se um cubo tem aresta a = 3cm, logo A = 6. 3² = 54 cm²
142

143. Matemática
O Paralelepípedo
Para calcular a área da superfície do paralelepípedo vamos planifica-lo:
À esquerda temos a imagem um paralelepípedo, que é formado por 6 retângulos. Porém, nem
todos os retângulos são iguais. Isto faz com que encontremos formas diferentes de paralelepípedos.
À direita temos sua planificação.
A área do retângulo é A = b . h. Para calcular a área da superfície de um paralelepípedo, temos
que calcular as áreas de todos os seis retângulos que o compõem e depois adicionar os resultados.
Exemplo:
Esse paralelepípedo tem dois retângulos de área = 7.3 = 21 cm²
Dois retângulos de A = 5.3 = 15 cm²
E dois retângulos de A = 7.5 = 35 cm²
Sendo assim, a área do paralelepípedo será 2 . (21 + 15 + 35) = 142 cm²
O cilindro
O cilindro tem na sua superfície, dois círculos iguais e um retângulo. Observe sua planificação.
Para calcular a área da superfície do cilindro temos que calcular a área dos dois círculos e da
superfície lateral (que é um retângulo), como mostra a figura anterior.
143

144. Matemática
Assim teremos:
Acilindro = 2 . Ácírculo + Álateral = 2 $ r $ r2 + 2 $ r $ r $ h = 2 $ r $ r^h + r h
Por exemplo, se neste cilindro a altura for 10 m e o raio da base é 5 m, então: h = 10 e r = 5.
A = 2 $ r $ 5^10 + 5h
A = 10r $ 15
A = 150r m2
Atividades
01 A área total da superfície de um cubo é igual a 54 cm². Calcule a medida da aresta deste cubo.
Sugestão de solução
A = 6.a²
54 = 6.a²
a² = 9
a = 3 cm
02 Maria tem uma caixinha de sapatos e quer decorá-la cobrindo-a com papel de presente. Esta é a caixinha de
Maria:
Quantos cm² ela vai gastar de papel para cobrir a caixinha?
Sugestão de solução
Área dos retângulos = 27 . 18 = 486 cm²
27 . 9 = 243 cm²
9 . 18 = 162 cm²
A = 2 . (486 + 243 + 162) = 2 . 891 = 1 782 cm²
Maria vai gastar 1 782 cm² de papel.
03 Uma indústria fabrica latas para embalagem em formato cilíndrico cujo raio da base mede 20 cm de comprimento e sua altura mede 80 cm. Para fabricação dessas latas, a indústria utiliza chapas metálicas. Quantos centímetros quadrados de chapa são necessários para fabricar uma lata? (use r = 3,14).
Sugestão de solução
r = 20 cm
h = 80 cm
A = 2 . π . r(h + r)
144

145. Matemática
A = 2 . 3,14 . 20 ( 80 + 20)
A = 125,6 . 100
A = 12 560 cm²
Serão necessários 12 560 cm² de chapa metálica.
Desafio
Em uma caixa de vidro com tampa, foi colocado um cilindro de cartolina como mostra a figura:
A caixa tem forma de um cubo de aresta 14 cm. Encontre cada uma das suas áreas e descubra qual das
duas figuras tem a maior superfície.
Sugestão de solução
A área do cubo será:
A = 6 . a² = 6 . 14² = 1 176 cm²
Como a aresta do cubo mede 14 cm o raio do cilindro será a metade, isto é, 7 cm, e a altura será 14 cm.
A = 2 $ r $ r^ h + r h
A = 2 $ r $ 7^14 + 7h
A = 14r $ 21 = 294r cm2
A área da superfície do cilindro é igual a 294 . 3,14 cm², que é, aproximadamente, 923,16 cm²
Logo, o cubo terá a maior superfície
145

146. Matemática
Aula 40
Exercícios envolvendo a área de
superfície de figuras não planas: cubo,
cilindro e paralelepípedo, aplicados em
avaliações externas
Objetivo geral
Compreender e calcular a medida da área de
superfície de figuras não planas: cubo, cilindro e
paralelepípedo, aplicados em avaliações externas.
Itens e questões
01 Observe o cubo a seguir.
O que devo aprender
nesta aula
u Compreender e utilizar as fórmulas
de área de figuras planas como
triângulo, losango, paralelogramo,
trapézio, retângulo, hexágono etc. e
de área de superfície de figuras não
planas como o cubo, o cilindro, e o
paralelepípedo.
A área dessa figura planificada é
(A) 8 cm2.
(B) 24 cm2.
(C) 64 cm2.
(D) 512 cm2.
Sugestão de solução
Sabemos que o cubo tem 6 faces iguais, para obter a medida da área total dessa figura planificada devemos
calcular o valor da área de uma face e em seguida multiplicar esse resultado por seis. Assim temos:
Área de uma face = 8 x 8 = 64 cm2.
Área total da figura planificada 64 x 6 = 512 cm2.
Portanto, a área da figura planifica será 512 cm2.
146

147. Matemática
02 A superfície total de um cilindro planificado como mostra a figura abaixo, é a reunião da superfície lateral com
os círculos das bases.
A área total da superfície desse cilindro é
(A) 28 r cm2
(B) 24 r cm2
(C) 20 r cm2
(D) 8 r cm2
Sugestão de solução:
Primeiramente, vamos calcular a área de um dos círculos e multiplicar o resultado por 2:
A = r $ r2 = r $ 22 = 4r cm2
Assim, a área dos dois círculos é igual a 2 $ 4r = 8r cm2 .
Em seguida, vamos calcular a área da superfície lateral (retângulo):
A = 2r $ r $ h = 4 r $ 5 = 20 r cm2
Logo, a área total da superfície desse cilindro será a soma da área dos dois círculos e do retângulo é:
8 r cm2 + 20 r cm2 + 28 r cm2
Portanto, a área total da superfície desse cilindro é 28 r cm2
03 Dado um paralelepípedo de dimensões como mostra a figura a seguir
147

148. Matemática
A medida da área total da superfície desse paralelepípedo é
(A) 8 cm2.
(B) 24 cm2.
(C) 48 cm2.
(D) 56 cm2.
Sugestão de solução:
Primeiramente, vamos calcular a medida da área de um dos quadrados e multiplicar o resultado por 2. Como
no quadrado temos l = 2 cm, basta fazer o seguinte calculo.
A = l x l = 2 x 2 = 4 cm2
Assim, a medida da área dos dois quadrados é A = 2 x 4 = 8 cm2.
Em seguida, vamos calcular a medida da área de um dos retângulos e multiplicar o resultado por 4. Como no
retângulo temos b = 2 cm e h = 6 cm, basta fazer o seguinte calculo.
A = b x h = 2 x 6 = 12 cm2
Assim, a medida da área dos quatro retângulos é A = 2 x 12 = 48 cm2.
Logo, a área total da superfície desse paralelepípedo será a soma da área dos dois quadrados e dos quatro
retângulos é:
8 cm2 + 48 cm2 = 56 cm2
Portanto, a medida da área total da superfície desse paralelepípedo é 56 cm2.
04 Em cada sólido representado a seguir, calcule a medida de sua área total
a)
Cilindro circular reto com 6 cm de raio da base e 12 cm de altura
b)
Medidas das arestas:
2 cm, 4 cm e 6 cm
148

149. Matemática
c)
Medida da aresta:
12 cm
Sugestão de ssolução:
a) 216 r cm2
b) 88 r cm2
c) 864 cm2
05 A aresta de um cubo cuja a medida da área de sua superfície corresponde à 294 cm2 é igual a:
a) 6 cm
b) 7 cm
c) 8 cm
d) 9 cm
Sugestão de solução:
b.
06 Determine a área lateral total de um paralelepípedo cujas dimensões são: 8 cm x 10 cm x 12 cm.
Sugestão de solução:
592 cm2
149

150. Matemática
Aula 41
Leitura de gráficos e tabelas
Objetivo geral
Apresentar conceitos básicos de estatística. Organizar os dados coletados em uma pesquisa, através de
tabela, para facilitar a análise.
O que devo aprender
nesta aula
u Construir tabelas e gráficos de
Conceitos básicos
frequências de dados estatísticos;
u Elaborar, oralmente ou por
Estatística: É uma ciência que atua na coleta de
escrito, conclusões com base em
dados (planejamento e obtenção dos dados), na sua
leitura, interpretação e análise
organização, descrição (resumo e apresentação dos
de informações apresentadas em
tabelas e gráficos.
dados) e análise dos dados (extrair conclusões para
tomada de decisões).
u Traduzir informações contidas em
tabelas e gráficos diversos.
População: Conjunto de todas as pessoas (objetos)
que têm em comum a característica que está sendo
analisada. Exemplo: Alunos da turma A
Amostra: É uma parte (parcela ou subconjunto) da população. Exemplo: alunos do sexo
masculino da turma A
Variável: É o item a ser avaliado na pesquisa.
A variável pode ser definida como qualitativa ou quantitativa.
Variável quantitativa: quando seus resultados forem numéricos, tais como:
peso, altura, idade, salário, etc.
Variável qualitativa: quando forem resultados de classificações em categorias que não são
números, tais como, cor, sexo, estado civil, religião, times de futebol, etc.
Tabela
É a forma de apresentar de forma resumida, através de colunas e linhas, um conjunto de dados.
A tabela deve ser construída de forma simples e conter informações claras e suficientes para o
entendimento do leitor. As informações são disponibilizadas no título (o quê,onde e quando se deu
a pesquisa), na fonte (indica onde foram coletados os dados) e nas colunas (variáveis e frequências).
Construção de tabela: A primeira coluna da tabela apresenta a variável e a segunda coluna
consiste nas frequências absolutas, ou seja, o número absoluto de ocorrências encontradas. Outras
colunas serão inseridas posteriormente, com a inclusão de novos conteúdos.
Elementos essenciais em uma tabela:
1. Título (aparece no topo da tabela) – É o local na tabela onde aparece o assunto (variável) que
está sendo apresentado, quando e onde ocorreu a pesquisa.
2. Corpo – São as colunas e as linhas da tabela onde aparecem informações sobre o assunto
(variável) em estudo.
150

151. Matemática
3. Fonte – Aparece no rodapé da tabela, é o local onde aparece o órgão ou instituição responsável
pela informação.
Exemplo: Colégio Estadual “Coronel Adamastor”, pesquisa realizada para obter a estatura
aproximada, em cm, dos alunos do turno noturno do ensino médio, no ano de 2011.
153
153
153
153
155
155
156
156
156
156
159
159
159
161
161
161
161
161
161
161
163
163
163
163
163
163
163
163
163
163
164
164
164
164
165
165
165
166
166
166
172
172
172
172
175
175
175
175
175
175
175
175
175
177
177
178
178
178
179
180
Para cada estatura contamos o número de ocorrências. Esse número obtido é chamado de
frequência absoluta (fa) que será representado na tabela abaixo:
153 (4)
155 (2)
156 (4)
159 (3)
161 (7)
163 (10) 164 (4)
165 (3) 166 (3)
172 (4)
175 (9) 177 (2)
178 (3)
179 (1)
180 (1)
Vamos à representação dos dados na tabela.
Tabela 1
Título
Cabeçalho e colunas
indicadoras
Corpo da tabela
Fonte
Estatura dos alunos do Ensino Médio/Noturno do Colégio Estadual
Coronel Adamastor – 2011
Estatura (cm)
Frequência absoluta (fa)
153
4
155
2
156
4
159
3
161
7
163
10
164
4
165
3
166
3
172
4
175
9
177
2
178
3
179
1
180
1
Total
60
Fonte: Secretaria do Colégio Estadual Coronel Adamastor
151

152. Matemática
Atividades
01 As salas de cinema de um shopping realizou em fevereiro de 2012, uma pesquisa com 30 pessoas, para saber
as preferências de seus frequentadores e obteve os seguintes resultados:
Modalidade de
filme
Pipoca durante
o filme
Pipoca e refrigerante
durante o filme
Preferem filme
dublado
Preferem filme
legendado
Romance
Sim
Não
Não
Sim
Ação
Não
Sim
Sim
Não
Comédia
Sim
Não
Não
Sim
Suspense
Não
Sim
Sim
Não
Ficção científica
Sim
Não
Sim
Não
Drama
Não
Sim
Não
Sim
Terror
Não
Sim
Sim
Não
Romance
Sim
Não
Não
Sim
Suspense
Sim
Não
Sim
Não
Ação
Sim
Não
Não
Sim
Suspense
Não
Sim
Sim
Não
Romance
Sim
Não
Não
Sim
Ação
Não
Sim
Não
Sim
Comédia
Sim
Não
Não
Sim
Suspense
Não
Sim
Sim
Não
Romance
Não
Sim
Sim
Não
Comédia
Não
Sim
Não
Sim
Ficção científica
Sim
Não
Sim
Não
Ação
Sim
Não
Não
Sim
Romance
Não
Sim
Não
Sim
Drama
Sim
Não
Não
Sim
Ação
Sim
Não
Sim
Não
Comédia
Sim
Não
Sim
Não
Terror
Sim
Não
Não
Sim
Romance
Não
Sim
Não
Sim
Suspense
Não
Sim
Sim
Não
Ação
Sim
Não
Sim
Não
Comédia
Não
Sim
Não
Sim
Suspense
Sim
Não
Não
Sim
Terror
Não
Sim
Não
Sim
A. Construa uma tabela de distribuição de frequência que representa a preferência das pessoas pesquisadas
que assistem alguma modalidade de filme, esse deve ser legendado e a pessoa pode estar comendo pipoca.
B. Construa uma tabela de distribuição de frequência que representa o gosto das pessoas por modalidade de
filme e assistem filme comendo pipoca e tomando refrigerante.
152

153. Matemática
Sugestão de solução
A. Para resolver a questão o aluno deve fazer a contagem do número de ocorrências das variáveis (três), levando em consideração a modalidade do filme, assistir filme legendado e comendo pipoca.
Tabela II – Salas de cinema de um shopping, tipos de filme legendados que as pessoas preferem, com a possibilidade de comer pipocas durante a seção – fevereiro de 2012.
Modalidade do filme (legendado)
fa
Romance
3
Comédia
2
Ação
2
Drama
1
Terror
1
Suspense
1
Total
10
Fonte: Gerência de markting das salas do cinema
B. Para resolver a questão o aluno deve fazer a contagem do número de ocorrências das variáveis (duas), levando em consideração a modalidade do filme, assistir filme comendo pipoca e tomando refrigerante.
Tabela III – Anápolis, salas de cinema de um shopping, tipos de filme que as pessoas preferem,
com a possibilidade de comer pipocas e tomar refrigerante durante a seção – fevereiro de 2012.
Modalidade do filme
fa
Ação
2
Suspense
4
Drama
1
Romance
3
Comédia
2
Terror
2
Total
14
Fonte: Gerência de markting das salas do cinema
02 Após a aplicação do teste de matemática (valor de zero a cem pontos) os alunos da turma do professor Aroldo
quiseram saber as notas de todos os colegas da sala, o professor sem falar o nome dos alunos foi ditando as notas
conforme apresentadas abaixo:
10
20
30
10
50
60
70
30
80
90
10
30
80
60
70
20
10
80
90
100
20
30
10
50
80
90
100
00
80
90
50
50
30
10
100
50
30
60
70
20
20
30
10
50
90
30
10
20
Organize as notas em ordem crescente ou decrescente (rol):
153

154. Matemática
Sugestão de solução
Para a solução desse exercício os alunos fazem a opção de colocar as notas em ordem crescente ou decrescente.
00
20
50
80
10
20
50
80
10
20
50
80
10
30
50
80
10
30
50
90
10
30
60
90
10
30
60
90
10
30
60
90
10
30
70
90
20
30
70
100
20
30
70
100
20
50
80
100
03 Aproveitando os dados do exercício anterior, represente as notas obtidas em uma tabela e em seguida responda:
•O
número de alunos que obtiveram notas inferiores a 50 pontos;
• O número de alunos que foram oprovadas no teste sabendo que a nota mínima é 60 pontos.
Sugestão de solução
Tabela III – Colégio Estadual Anísio Teixeira, notas dos alunos
de matemática da 3ª série do ensino médio, dezembro de 2011.
Notas
fa
00
1
10
8
20
6
30
8
50
6
60
3
70
3
80
5
90
5
100
3
Total
48
• 23 alunos obtiveram notas inferiores a 50 pontos.
• 19 alunos foram aprovados no teste.
Desafio
No inicio do ano de 2012, a bibliotecária da Escola Municipal “José Antônio da Fonseca” precisava identificar
os 200 (duzentos) livros de matemática, os 150 (cento e cinquenta) livros de física, os 280 (duzentos e
oitenta) livros de língua portuguesa, que estavam nas estantes da biblioteca. Deve organizar os livros de
forma a ficarem juntos em cada estante, os livros separados por disciplina e por editora. A bibliotecária
precisa saber também o número de livros de cada editora. A professora de Matemática ficou encarregada de
organizar os livros, para isso ela contou com a participação de seus alunos que foram dividos em três grupos.
Os dados foram organizados em uma tabela de distribuição de frequência.
154

155. Matemática
Sugestão de solução
Tabela IV – Escola Municipal de Aparecida de Goiânia, número de livros da
disciplina de matemática por editora – 2012.
Editora
fa
Ática
80
Saraiva
62
Moderna
58
Total
200
Fonte: Alunos da 3ª série do ensino médio da Escola Municipal de Aparecida de Goiânia.
Professor:
1. Além do desafio de construir a tabela, realizar a contagem dos livros por editara o professor
pode utilizar a ida dos alunos à biblioteca e instigá-los à pesquisa, ao estudo;
2.
Uma ótima maneira de dispertar interesse no aluno ao trabalhar estatística é utilizar o
laboratório de informática, utilizando o Excel ou programa semelhante na construção das
tabelas e gráficos.
Aula 42
Construir tabelas de dados estatísticos
Objetivo geral
Apresentar alguns conceitos básicos de estatística.
Organizar os dados coletados em uma pesquisa,
através de tabela, para facilitar a análise.
O que devo aprender
nesta aula
u Construir tabelas e gráficos de
Conceitos básicos
frequências de dados estatísticos.
População: Conjunto de pessoas (objetos) que têm
em comum a característica que está sendo analisada.
Por exemplo: um grupo de estudantes de determinada escola; pessoas residentes em um mesmo
bairro etc.
Amostra: É uma parte (parcela ou subconjunto) da população.
Variável: É o item a ser avaliado na pesquisa.
A variável pode ser definida como qualitativa ou quantitativa. As variáveis que exprimem
contagem, números, quantidade, são as variáveis quantitativas, enquanto as que exprimem
qualidade são chamadas variáveis qualitativas.
155

156. Matemática
Como exemplos de variáveis quantitativas temos idade, altura, salários, dentre outros e de
variáveis qualitativas, cor dos olhos, tipos de transporte, times de futebol dentre outros.
Tabela: é a forma de apresentar de forma sintetizada, por meio de colunas e linhas, um conjunto
de dados.
A tabela deve ser construída de forma simples e conter informações suficientes para o
entendimento do leitor. As informações são disponibilizadas no título (local da pesquisa, conteúdo
e data da pesquisa), na fonte (indica onde foram coletados os dados) e nas colunas (variáveis e
frequências).
Elementos essenciais em uma tabela
1. Título (aparece no topo da tabela) – É o local na tabela onde aparece o assunto (variável) que
está sendo apresentado, quando e onde ocorreu a pesquisa.
2. Corpo – São as colunas e as linhas da tabela onde aparecem informações sobre o assunto
(variável) em estudo.
3. Fonte – Aparece no rodapé da tabela, é o local onde aparece o órgão ou instituição responsável
pela informação.
Portanto, é imprescindível que ao se trabalhar com tabelas se evidencie o máximo de
informações possíveis acerca da mesma afim de evidenciar o maior número de dados para o leitor.
Observe o exemplo:
A tabela seguir expressa os dados obtidos em uma pesquisa realizada para obter a altura
aproximada, em cm, dos alunos do ensino médio ( turno noturno) do Colégio Estadual “Paulo
Freire”, no ano de 2011.
153
153
153
153
155
155
156
156
156
156
159
159
159
161
161
161
161
161
161
161
163
163
163
163
163
163
163
163
163
163
164
164
164
164
165
165
165
166
166
166
172
172
172
172
175
175
175
175
175
175
175
175
175
177
177
178
178
178
179
180
Observe que a partir dos dados apresentados na tabela o passo seguinte será a organização
dos mesmos para otimizarmos o processo estatístico. Sendo assim, para cada medida de altura
informada contamos o número de ocorrências. Esse número obtido é chamado de frequência
absoluta (fa) que será representado na tabela, conforme abaixo:
153 (4)
155 (2)
156 (4)
159 (3)
161 (7)
163 (10)
172 (4)
175 (9)
177 (2)
178 (3)
179 (1)
180 (1)
Vamos à representação dos dados na tabela.
156
164 (4)
165 (3)
166 (3)

157. Matemática
Tabela II – Colégio Estadual “Paulo Freire” - Altura dos alunos do ensino
médio noturno - 2011
Altura (cm)
fa
153
4
155
2
156
4
159
3
161
7
163
10
164
4
165
3
166
3
172
4
175
9
177
2
178
3
179
1
180
1
Total
60
Fonte: Secretaria do Colégio.
Atividades
01 O cinema de um shopping realizou em fevereiro de 2012, uma pesquisa com 30 pessoas, para saber as preferências de seus frequentadores conforme discriminado na tabela abaixo:
Modalidade de
filme
Pipoca durante
o filme
Pipoca e refrigerante
durante o filme
Preferem filme
dublado
Preferem filme
legendado
Romance
Sim
Não
Não
Sim
Ação
Não
Sim
Sim
Não
Comédia
Sim
Não
Não
Sim
Suspense
Não
Sim
Sim
Não
Ficção científica
Sim
Não
Sim
Não
Drama
Não
Sim
Não
Sim
Terror
Não
Sim
Sim
Não
Romance
Sim
Não
Não
Sim
Suspense
Sim
Não
Sim
Não
Ação
Sim
Não
Não
Sim
(continua)
157

158. Matemática
Modalidade de
filme
Pipoca durante
o filme
Pipoca e refrigerante
durante o filme
Preferem filme
dublado
Preferem filme
legendado
Suspense
Não
Sim
Sim
Não
Romance
Sim
Não
Não
Sim
Ação
Não
Sim
Não
Sim
Comédia
Sim
Não
Não
Sim
Suspense
Não
Sim
Sim
Não
Romance
Não
Sim
Sim
Não
Comédia
Não
Sim
Não
Sim
Ficção científica
Sim
Não
Sim
Não
Ação
Sim
Não
Não
Sim
Romance
Não
Sim
Não
Sim
Drama
Sim
Não
Não
Sim
Ação
Sim
Não
Sim
Não
Comédia
Sim
Não
Sim
Não
Terror
Sim
Não
Não
Sim
Romance
Não
Sim
Não
Sim
Suspense
Não
Sim
Sim
Não
Ação
Sim
Não
Sim
Não
Comédia
Não
Sim
Não
Sim
Suspense
Sim
Não
Não
Sim
Terror
Não
Sim
Não
Sim
1. Construa uma tabela de distribuição de frequência que represente o número de pessoas que estejam comendo pipoca e assistam a alguma modalidade de filme que seja legendado.
2. Construa uma tabela de distribuição de frequência que represente o gosto das pessoas por modalidade de
filme e levem em consideração as pessoas que estejam comendo pipoca e tomando refrigerante:
Sugestão de solução
Item 1 - Para resolver a questão o aluno deverá fazer a contagem do número de ocorrências das variáveis (três),
levando em consideração a modalidade do filme, assistir filme legendado e comendo pipoca.
Modalidade do filme (legendado)
fa
Romance
3
Comédia
2
Ação
2
Drama
1
Terror
1
Suspense
1
Total
10
Fonte: Gerência de markting das salas do cinema
158

159. Matemática
Item 2 - Para resolver a questão o aluno deverá fazer a contagem do número de ocorrências das variáveis
levando em considerações a modalidade do filme e comer pipoca e tomar refrigerante.
Modalidade do filme
fa
Ação
2
Suspense
4
Drama
1
Romance
3
Comédia
2
Terror
2
Total
14
Fonte: Gerência de markting das salas do cinema.
02 Após a aplicação do teste de matemática (valor de zero a cem pontos) os alunos da turma do professor Aroldo
quiseram sabem as notas de todos os colegas da sala. O professor sem falar o nome dos alunos ditou as notas conforme
apresentadas a seguir:
10
20
30
10
50
60
70
30
80
90
10
30
80
60
70
20
10
80
90
100
20
30
10
50
80
90
100
00
80
90
50
50
30
10
100
50
30
60
70
20
20
30
10
50
90
30
10
20
20
30
70
100
20
30
70
100
20
50
80
100
Organize as notas em ordem crescente ou decrescente (rol):
Sugestão de solução
00
20
50
80
10
20
50
80
10
20
50
80
10
30
50
80
10
30
50
90
10
30
60
90
10
30
60
90
10
30
60
90
10
30
70
90
03 Aproveitando os dados do exercício anterior, represente as notas obtidas em uma tabela e em seguida res-
ponda:
• Qual a quantidade de alunos que obtiveram notas inferiores a 50 pontos?
• Qual a quantidade de alunos que obtiveram a nota mínima de 60 pontos?
Sugestão de solução
Notas
00
10
20
30
fa
1
8
6
8
(continua)
159

160. Matemática
Notas
50
60
70
80
90
100
Total
fa
6
3
3
5
5
3
48
• 23 alunos obtiveram notas inferiores a 50 pontos.
• 19 alunos foram aprovados no teste.
Desafio
A partir dos dados apresentados na tabela a seguir, construa o rol determinando a quantidade de coleções
por disciplina, editora e coleção.
Disciplina
Língua portuguesa
Geografia
Geografia
Língua portuguesa
Língua portuguesa
Matemática
Matemática
Matemática
Língua portuguesa
Geografia
Matemática
Matemática
Matemática
Geografia
Língua portuguesa
Língua portuguesa
Geografia
Matemática
160
Editora
Editora A
Editora B
Editora B
Editora C
Editora C
Editora B
Editora C
Editora A
Editora A
Editora C
Editora C
Editora B
Editora B
Editora A
Editora A
Editora C
Editora C
Editora B
Coleção
Ensino Fundamental I
Ensino Fundamental II
Ensino Fundamental I
Ensino Fundamental II
Ensino Fundamental I
Ensino Fundamental II
Ensino Fundamental I
Ensino Fundamental I
Ensino Médio
Ensino Fundamental I
Ensino Fundamental II
Ensino Médio
Ensino Médio
Ensino Fundamental II
Ensino Fundamental II
Ensino Médio
Ensino Médio
Ensino Médio
(continua)

161. Matemática
Disciplina
Geografia
Língua portuguesa
Matemática
Matemática
Língua portuguesa
Língua portuguesa
Matemática
Língua portuguesa
Geografia
Editora
Editora C
Editora B
Editora B
Editora A
Editora B
Editora C
Editora A
Editora A
Editora A
Coleção
Ensino Fundamental II
Ensino Fundamental I
Ensino Fundamental I
Ensino Médio
Ensino Fundamental II
Ensino Médio
Ensino Fundamental II
Ensino Médio
Ensino Fundamental I
Aula 43
Construir gráficos de frequência de
dados estatísticos – coluna
Objetivo geral
Apresentar dados de uma pesquisa de forma
simples, através do gráfico em colunas, despertando
no aluno o interesse pela leitura e interpretação de
dados.
O que devo aprender
nesta aula
u Construir tabelas e gráficos de
frequências de dados estatísticos;
Conceito básico
Gráfico – Representação dos dados da tabela de
forma simples e clara.
Os gráficos de colunas, barras, linhas, dentre
outros são construídos utilizando o sistema de
coordenadas cartesianas (são os gráficos que estão
representados em forma de retângulo), enquanto
outros utilizam o sistema de coordenadas polares
(círculo trigonométrico). Um exemplo de gráfico no
círculo trigonométrico é o gráfico de setores.
u Elaborar, oralmente ou por
escrito, conclusões com base em
leitura, interpretação e análise
de informações apresentadas em
tabelas e gráficos.
u Traduzir informações contidas em
tabelas e gráficos diversos.
No gráfico é necessário colocar o título, a fonte e demais informações que sejam necessárias ao
entendimento dos dados.
161

162. Matemática
Gráfico em colunas
Gráficos de colunas são úteis para mostrar as alterações de dados em um período de tempo ou
para ilustrar comparações entre itens.
Observação:
1. Largura: definida no eixo horizontal (eixo x). As bases das colunas, bem como os espaços que
devem ser colocados entre cada coluna, devem possuir dimensões padronizadas.
2. Altura: definida no eixo vertical (eixo y), a altura deve corresponder à frequência absoluta
(fa).
Exemplo:
Vamos considerar a tabela construída nas atividades da aula anterior
Tabela I – Salas de cinema de um shopping, tipos de filme legendado que as pessoas
preferem, com a possibilidade de comer pipocas durante a seção – fevereiro de 2012.
Modalidade do filme (legendado)
fa
Romance
3
Comédia
2
Ação
2
Drama
1
Terror
1
Suspense
1
Total
10
Fonte: Gerência de markting das salas do cinema
Gráfico em colunas
Fonte: Gerência de markting das salas do cinema
162

163. Matemática
Atividades
01 Às pessoas presentes a um evento automobilismo foi feita a seguinte pergunta: Qual a sua marca de carro
preferida? Na tabela a seguir está representada a preferência dos entrevistados.
Tabela II – Preferência por marcas de carro das pessoas presentes em evento automobilístico.
Marcas
fa
Ford
8
Fiat
6
GM
12
Nissan
2
Peugeot
3
Volks
10
Total
48
Fonte: Organizadores do evento.
Os organizadores do evento, com o objetivo de divulgar o resultado nas mídias, solicitou que esses dados
fossem representados em gráfico de colunas. Então, essa é a sua tarefa, represente os dados da tabela em um
gráfico de colunas.
Sugestão de solução
Fonte: Organizadores do evento.
163

164. Matemática
02 O gráfico a seguir apresenta a distância percorrida diariamente até uma das Unidades da UEG, dos inscritos e
aprovados nos vestibulares, nos anos de 2010, 2011 e 2012.
Fonte: Núcleo de Seleção da UEG.
Observando o gráfico e as alternativas abaixo, podemos afirmar que:
a) O número de inscritos e aprovados, que residem em até 20 (vinte) km da UEG, representa a menor frequência nos anos pesquisados.
b) Menos de 10% (dez por centro) dos inscritos e aprovados nos três vestibulares, residem há mais de 100
(cem) km da escola.
c) O número de inscritos no ano de 2011/1, que residem entre 21 a 50 km é aproximadamente 30% (trinta por
cento).
d) No ano de 2012 o maior índice encontrado foi relativo aos inscritos que residem até 20 (vinte) km da UEG.
Sugestão de solução:
Alternativa correta = “b”
Justificando as demais alternativas:
a) Os residentes em até 20 (vinte) km da UEG representa em todos os itens um maior índice;
c) A resposta correta seria aproximadamente 20% (vinte por cento);
d) A resposta correta nessa alternativa séria em relação aos aprovados.
164

165. Matemática
Desafio
Os professores de Educação Física, Biologia, Química e Matemática organizaram um momento de estudo/
integração entre os alunos do 9° ano do ensino fundamental de um colégio. Um dos aspectos observados
foi o lanche oferecido pela escola.
Tabela III – Preferência pelos lanches oferecidos aos alunos do
9° ano do ensino fundamental de um colégio
Cardápio
fa
Galinhada
68
Bolacha com suco
22
Farrofa
35
Arroz doce
12
Feijão tropeiro
58
Pão com carne moída
45
Cachorro quente
50
Total
290
Após pesquisa de opinião, os professores observaram que a preferência dos alunos foi pela galinhada. Aos
professores de Educação Fisica, Biologia e Quimica cabe a tarefa de juntamente com os alunos, realizarem
um estudo sobre os benefícios de cada alimento e os cuidados que devem ser adotados para uma alimentação balanceada. Ao professor de matématica em parceria com os alunos fica a responsabilidade de
representar o gráfico em colunas que retrate a tabela acima. Ajude o professor de matemática construindo
o gráfico.
Sugestão de solução
165

166. Matemática
Aula 44
Construção de gráficos de frequência
de dados estatísticos – barra
Objetivo geral
Construir e interpretar tabelas e gráficos em
barras.
O que devo aprender
nesta aula
Conceito básico
Gráfico é uma representação utilizada para ajudar
a leitura e compreensão de dados numéricos. Por
ter uma visualização fácil ele auxilia a compreensão
das informações que desejamos comunicar. Existem
vários tipos de gráficos, neste momento estudaremos
o gráfico em barras.
u Construir tabelas e gráficos de
frequências de dados estatísticos;
u Elaborar, oralmente ou por
escrito, conclusões com base em
leitura, interpretação e análise
de informações apresentadas em
tabelas e gráficos.
u Traduzir informações contidas em
Gráfico em barras
tabelas e gráficos diversos.
O gráfico em barras é muito usado para comparar
quantidades. As barras podem aparecer na vertical ou
na horizontal, onde também são chamadas de colunas.
Dicas para interpretar o gráfico em barras:
• O eixo vertical apresenta quais valores ou grandezas (porcentagem, valores numéricos,
temperaturas, peso etc.) serão expressas.
• O eixo horizontal apresenta qual categoria (tempo, países, produção, sexo, períodos etc.)
deverá ser apresentada.
Exemplo
A tabela e o gráfico a seguir foram construídos a partir de uma pesquisa na escola BOA NOTA,
sobre as frutas preferidas dos estudantes.
Frutas Preferidas
Quantidade de Alunos
Banana
Pera
10
Uvas
25
Maçãs
166
15
20

167. Matemática
Atividades
01 O Brasil é formado por 5 (cinco) regiões, 26 (vinte e seis) Estados, o Distrito Federal e por 5564 (cinco mil, qui-
nhentos e sessenta e quatro) municípios.
Na tabela abaixo apresentamos os 10 (dez) Estados com maior número de municípios.
Tabela 02 - Estados brasileiros com maior número de municípios - 2012
Estados
Bahia
Goiás
Maranhão
Minas Gerais
Paraíba
Paraná
Piauí
Rio Grande do Sul
Santa Catarina
São Paulo
Municípios
417
246
217
853
223
399
224
496
293
645
Fonte: Disponível em: http://www.portalbrasil.net/brasil.htm. Acesso em: 06 de dez. 2012.
Dados atualizados até 29.11.2012
Com os dados apresentados na tabela acima, construa o gráfico em barras:
167

168. Matemática
Sugestão de solução
ou
02 Considerando os mesmos Estados do exercício 01, com a variável em análise sendo a população em cada
Estado, observe o gráfico em barras a seguir:
168

169. Matemática
Fonte: Disponível em: http://www.portalbrasil.net/brasil.htm. Acesso em: 06 de dez. 2012.
Analise o gráfico e responda:
a) Os Estados brasileiros citados no gráfico, representam mais de 60% (sessenta por cento) da população brasileira? Por que?
b) Coloque os Estados representados no gráfico em ordem crescente de acordo com a população em cada
Estado.
c) O Estado de São Paulo representa mais que1/4 da população brasileira?
d) Sendo a população brasileira composta de 190.732.694 habitantes, então Goiás possui mais de 7.000.000 de
habitantes?
Sugestão de solução:
a) Sim, pois: 21,6 + 3,3 + 5,6 + 1,6 + 5,5 + 2,0 + 10,3 + 3,4 + 3,1 + 7,3 = 63,7
Justificando as demais alternativas:
b) A sequência correta dos Estados em ordem crescente segundo a população é Piauí, Paraíba, Goiás, Santa
Catarina, Maranhão, Paraná, Rio Grande do Sul, Bahia, Minas Gerais e São Paulo.
c) São Paulo representa menos que 1/4 ou 25% da população brasileira;
d) Goiás possui aproximadamente 6.000.000 de habitantes = 190.732.694 x 3,1%.
03 Densidade demográfica ou densidade populacional é o quociente entre a população total de uma região e a
sua superfície. Geralmente é expressa em quilômetros quadrados. O Brasil tem uma densidade populacional de 22,4
hab./km2.
169

170. Matemática
Observe o gráfico:
Disponível em: http://www.portalbrasil.net/brasil.htm. Acesso em: 08 de dez. 2012.
Com os dados apresentados acima, podemos afirmar que:
a) A densidade populacional na Bahia indica que o Estado possui o maior número de habitantes por quilometro
quadrado;
b) São Paulo é o Estado que possui o menor número de habitantes por quilometro quadrado;
c) Piauí é dos Estados apresentados no gráfico, o 9° em maior número de habitantes por quilometro quadrado;
d) Goiás possui maior número de habitantes por quilometro quadrado em relação ao Estado de Rio Grande do
Sul.
Sugestão de solução
Alternativa correta = item “c”
Justificando as demais alternativas:
a) Bahia possui menor número de habitantes por quilometro quadrado;
b) São Paulo possui maior número de habitantes por quilometro quadrado;
d) Goiás possui menor número de habitantes por quilometro quadrado em relação ao Estado de Rio Grande
do Sul.
170

171. Matemática
Desafio
Observe os gráficos III (atividade 02) e IV (atividade 03)
Analise criticamente os dois itens a seguir:
a) São Paulo representa um Estado brasileiro com maior número de habitantes e com maior
densidade demográfica.
b) Goiás possui uma população que representa 3,1% (três vírgula um por cento) da população
brasileira e uma densidade demográfica menor que 10 (dez) habitantes por quilometro quadrado.
Sugestão de solução
a) Alternativa correta. São Paulo representa o Estado brasileiro com maior número de habitantes
(21,6%, da população brasileira) e possui uma densidade demográfica de 166,24 habitantes por
quilometro quadrado, que é a maior dos Estados brasileiros.
b) Alternativa correta no item população, onde Goiás representa 3,1% (três vírgula um por cento) da população brasileira. E errada no item densidade demográfica, pois Goiás possui densidade demográfica de 17,65, maior que 10 (dez) habitantes por quilometro quadrado.
171

172. Matemática
Aula 45
Construção de gráficos de frequência
de dados estatísticos – setores
Objetivo geral
Construir e interpretar tabelas e gráficos de setores.
Conceito básico
Gráfico em setores – também chamado de gráfico
circular ou gráfico de pizza, é construído no círculo
trigonométrico, sendo o círculo dividido em setores
circulares. Por exemplo:
O que devo aprender
nesta aula
u Construir tabelas e gráficos de
frequências de dados estatísticos;
u Elaborar, oralmente ou por
escrito, conclusões com base em
leitura, interpretação e análise
de informações apresentadas em
tabelas e gráficos.
u Traduzir informações contidas em
tabelas e gráficos diversos.
Para representar os dados em um gráfico de setores (manualmente) é preciso que os valores
estejam em graus. Para isso, devemos definir na tabela duas novas colunas: a coluna da porcentagem
e a coluna dos graus.
Exemplo
Com os dados apresentados na tabela a seguir, construa o gráfico de setores.
Tabela 01 - Idade dos alunos do 3° ano do ensino médio de uma Escola.
Idade
%
Grau
15
17
38
136
16
14
31
112
17
14
31
112
Total
172
fa
45
100
360

173. Matemática
Sugestão de solução
Etapas:
 Para calcular os graus de cada setor, devemos primeiro calcular a porcentagem de cada
ocorrência (calculada dividindo cada fa pelo total de ocorrências). Em seguida devemos
calcular a nova coluna (graus), calculada por regra de três, conforme abaixo:
 360º – 100%
x = 136º
 38º – x
 Desenhe um círculo de tamanho adequado e represente o gráfico.
(interessante o aluno ter compasso e transferidor)
Atividades
01 Represente os dados abaixo em gráfico de setores:
Tabela 04 - Estados brasileiros, habitantes por km2 (dados arredondados) – 2012.
Estados
Bahia
Goiás
Maranhão
Minas Gerais
Paraíba
Paraná
Piauí
Rio Grande do Sul
fa
3
18
20
33
67
52
12
40
Santa Catarina
65
São Paulo
166
Fonte: Disponível em: http://www.portalbrasil.net/brasil.htm. Acesso em: 06 de dez. 2012.
Dados atualizados até 29.11.2012
173

174. Matemática
Sugestão de solução
02 O gráfico abaixo representa as seis principais agências bancárias em Joinville – Santa Catarina.
Disponível em: <http://br.bing.com/images/search?q=ibge+cidades&view=detail&id=4C442B614B
99F5DC1B71488B38DB8CB56736954C>. Acesso em: 08 de dez. 2012.
Observe os dados apresentados no gráfico de setores acima e responda:
a) As agências do Banco Real, somadas as agências do Banco Itaú, representam 15% das agências da cidade;
b) As agências dos bancos do Brasil, Bradesco e Itaú representam percentualmente igual ao percentual das
outras agências;
c) Considerando que em Joinville possui 82 agências bancárias, podemos dizer que o Banco do Brasil possui
11 (onze) agências bancárias;
Sugestão de solução
Alternativa correta = item “b”
Justificando as demais alternativas:
a) A soma das agências do Banco Real com as agências do Banco Itaú totalizam 12%;
c) O banco do Brasil possui 9 agências na cidade de Joinville.
174

175. Matemática
03 No campeonato brasileiro 2012, série “A”, os times fizeram 111 (cento e onze) gols antes de completarem 15
(quinze) minutos de partida. O gráfico em setores a seguir representa os percentuais.
Disponível em: http://esporte.uol.com.br/futebol/campeonatos/brasileiro/2012/
serie-a/estatisticas/A. Acesso em: 08 de dez. 2012.
Considerando o gráfico e o fato que os times nesse campeonato conseguiram fazer 111 (cento e onze) gols
em menos de 15 (quinze) minutos de partida, represente os dados em uma tabela, colocando o número de
gols de cada time.
Sugestão de solução
Com o cálculo de regra de três o aluno consegue a tabela abaixo:
Times
Número de gols
Atlético-GO
Coritiba
São Paulo
Palmeiras
Botafogo
Flamengo
Santos
Outros
Total
9
9
9
8
7
7
6
56
111
175

176. Matemática
Desafio
Ainda sobre o campeonato brasileiro série “A”, o gráfico e a tabela a seguir apresentam os números de Gols
feitos com o pé direito, pé esquerdo e cabeça.
Forma
Cabeça
Pé direito
Pé esquerdo
Total
fa
210
492
229
931
Considerando os primeiros colocados em cada item: - São Paulo, com 39 (trinta e nove) gols de pé direito;
- Atlético-MG, com 18 (dezoito) gols de cabeça e Grêmio, 19(dezenove) gols com pé esquerdo, complete
a tabela abaixo.
Time
São Paulo
Atlético-MG
Grêmio
Porcentagem na categoria
Sugestão de solução
Basta calcular as porcentagens a que pertence cada time conforme abaixo:
São Paulo – categoria gols com pé direito
492 gols – 100%
x = 7,9%
39 gols – x
Atlético – MG – categoria gols de cabeça
210 gols – 100%
x = 8,6%
18 gols – x
Grêmio – categoria gols com pé esquerdo
229 gols – 100%
x = 8,3%
19 gols – x
Time
São Paulo
Atlético-MG
Grêmio
176
Porcentagem na categoria
7,9%
8,6%
8,3%

177. Matemática
Aula 46
Conclusões com base na leitura
de gráficos
Objetivo geral
Ler e interpretar dados apresentados em gráficos diversos.
Conceito básico – Uma conversa.
A matemática deve proporcionar e estimular
o estudante a entrar em contato com o mundo das
informações, analisando e interpretando-as através
dos vários tipos de gráficos.
As atividades envolvendo tabulação de dados e
construções de gráficos precisam ser supervisionadas pelo professor.
O que devo aprender
nesta aula
u Construir tabelas e gráficos de
frequências de dados estatísticos;
u Elaborar, oralmente ou por
escrito, conclusões com base em
leitura, interpretação e análise
de informações apresentadas em
tabelas e gráficos.
u Traduzir informações contidas em
tabelas e gráficos diversos.
Atividades
01 A maioria dos brasileiros ainda não tem acesso à rede de esgoto. A maior parte dos domicílios brasileiros não
tinha, em 2008, acesso à rede geral de esgoto e, nesse quesito, havia uma enorme discrepância entre as regiões brasileiras. Essas conclusões foram apontadas na última Pesquisa Nacional de Saneamento Básico, divulgada pelo IBGE.
O gráfico mostra o percentual de municípios por Estado que fazem tratamento do esgoto.
Fonte: Disponível em: <http://noticias.uol.com.br/cotidiano/ultimas-noticias/2010/08/20/maioria-dos-brasileiros-ainda-nao-temacesso-a-rede-de-esgoto-diz-ibge.htm>. Acesso em: 09 de dez. 2012.
177

178. Matemática
De acordo com o gráfico analise as informações:
a) Os Estados de Goiás, Acre e Amapá, juntos totalizam o mesmo número percentual no tratamento de esgoto
em relação ao Estado de Ceará.
b) O Estado de Pernambuco oferece tratamento de esgoto 3(três) vezes a mais que o Estado de Sergipe.
c) De São Paulo para a direita, as cidades aparecem em ordem decrescente dos Estados que oferecem tratamento de esgoto.
d) Da direita para esquerda os Estados apresentam uma queda na oferta do tratamento de esgoto.
Sugestão de solução
Alternativa correta = item “c”
Justificando as demais alternativas
a) Goiás, Acre e Amapá = 55,1 e Ceará = 48,9
b) Pernambuco = 27,6 Sergipe = 9,3. Portanto. Três vezes = 27,9.
d) Da direita para esquerda há um crescimento na oferta de tratamento de esgoto.
02 Votos obtidos na eleição 2010 (1° turno), para Presidente da República no município de Goiânia.
Fonte: Disponível em: <http://www.tse.jus.br/eleicoes/eleicoes-anteriores/eleicoes-2010/estatisticas>. Acesso em: 10 de dez. 2012.
Sobre o resultado da eleição, de acordo com os dados oferecidos no gráfico, é correto afirmar que
a) A candidata Dilma Rousseff obteve o maior número de votos.
b) Considerando que 703.159 (setecentos e três mil, cento e cinquenta e nove) eleitores votaram em um dos
candidatos, Marina da Silva obteve mais de um quarto dos votos.
c) Os votos de Marina da Silva, José Serra e Dilma Rousseff totalizam mais de setecentos mil votos.
d) José Serra ficou classificado em primeiro lugar no resultado das eleições.
178

179. Matemática
Sugestão de solução
Alternativa correta = item “d”
Justificando as demais alternativas
a) Dilma ficou em segundo lugar no resultado final.
.
b) 7034159 = 175, 8 Marina da Silva = 173.398.
c) Totalizam 691.598 votos.
03 Eleições 2010 (2° turno), para Presidente da República no município no Goiânia.
Fonte: Disponível em: <http://www.tse.jus.br/eleicoes/eleicoes-anteriores/eleicoes-2010/estatisticas>. Acesso em: 10 de dez. 2012.
Com base nestas informações, analise criticamente as afirmativas:
a) Considerando os votos em um dos dois candidatos, pode-se dizer que José Serra obteve mais de 60% (sessenta por cento) dos votos.
b) Dilma Rousseff obteve aproximadamente 42% (quarenta e dois por cento) dos votos.
Sugestão de solução
Alternativa correta = item “b”
Justificando a outra alternativa
a) José Serra obteve aproximadamente 57,57% (cinquenta e sete vírgula cinquenta e sete por cento) dos votos.
179

180. Matemática
Desafio
A dengue é uma doença infecciosa febril aguda causada por um vírus da família Flaviridae e é transmitida,
no Brasil, através do mosquito Aedes Aegypti, também infectado pelo vírus.
Atualmente, a dengue é considerada um dos principais problemas de saúde pública de todo o mundo.
Fonte: Disponível em:<Leia mais: http://www.combateadengue.com.br/o-que-e-dengue/#ixzz2EhlLmQQZ>.
De acordo com o gráfico, responda:
a) Em quais períodos acontece crescimento dos casos de dengue no Brasil?
b) Considerando que no ano de 2002 ocorreram 800.000(oitocentos mil) casos de notificações de dengue
e que, no ano de 2003 ocorreram 350.000 (trezentos e cinquenta mil) casos, qual o percentual de queda
nos índices de notificações?
Sugestão de solução
a) Teve crescimento nos períodos de = 1990 a 1991; 1993 a 1998; 1999 a 2002 e 2004 a 2007.
b) Percentual aproximado de 43,75%.
180

181. Matemática
Aula 47
Relacionar gráficos com tabelas
Objetivo geral:
Relacionar e interpretar dados apresentados em gráficos com os dados apresentados em tabelas.
Conceito básico
Gráficos
Os gráficos representam o desempenho de um
conjunto de dados que se identificam e podem ser
confrontados instantaneamente.
Tabela
É a organização dos dados de uma determinada
informação como também a organização dos
resultados de uma pesquisa. Os dados ficam dispostos
em linhas e colunas, o que possibilita uma visão geral
dos resultados.
O que devo aprender
nesta aula
u Elaborar, oralmente ou por
escrito, conclusões com base em
leitura, interpretação e análise
de informações apresentadas em
tabelas e gráficos.
u Traduzir informações contidas em
tabelas e gráficos diversos.
Orientação para análise dos gráficos e tabelas
Leia com atenção o que é perguntado no problema e confronte os questionamentos com os
dados apresentado nos gráficos e nas tabelas.
Exemplo de atividade:
O órgão de defesa do consumidor – PROCOM, realizou uma pesquisa de preço sobre um
determinado produto. O resultado da pesquisa está disposto no gráfico a seguir:
181

182. Matemática
Das tabelas a seguir, a que melhor apresenta os dados relacionados ao gráfico é
a)
Lojas
Pesquisa de Preço
Valor em R$
América
80
Beto’s
90
Lima
40
Masad
50
Pains
60
b)
Pesquisa de Preço
Lojas
Valor em R$
América
90
Beto’s
80
Lima
40
Masad
50
Pains
60
c)
Pesquisa de Preço
Lojas
Valor em R$
América
80
Beto’s
90
Lima
50
Masad
40
Pains
60
d)
Pesquisa de Preço
Lojas
Valor em R$
América
80
Beto’s
90
Lima
50
Masad
60
Pains
40
Sugestão solução:
Conforme a orientação dada, o aluno poderá relacionar os dados apresentados no gráfico e relacioná-los à
tabela.
182

183. Matemática
Pesquisa de Preço
lojas
América
Beto’s
Pains
Masad
Lima
Valor em R$
90
80
60
50
40
Solução:
Alternativa “b”
Atividades
01 O gráfico a seguir apresenta o desempenho dos alunos em uma avaliação de matemática.
Das alternativas a seguir, qual representa a leitura dos dados do gráfico do desempenho na disciplina de matemática?
183

184. Matemática
a)
b)
Desempenho
Ótimo
Bom
Regular
Ruim
fa
Desempenho
Ótimo
Bom
Regular
Ruim
35%
35%
25%
15%
b)
fa
25%
15%
25%
15%
c)
Desempenho
Ótimo
Bom
Regular
Ruim
fa
Desempenho
Ótimo
Bom
Regular
Ruim
25%
35%
55%
15%
fa
25%
35%
25%
15%
Resposta
Alternativa “d”
02 O gráfico a seguir representa a preferência por modalidades esportivas.
A forma correta de representar esses dados em tabela é:
a)
Modalidade
Futebol
Vôlei
Basquete
Natação
Outros
184
fa (%)
40
30
5
10
15
b)
Modalidade
Futebol
Vôlei
Basquete
Natação
Outros
fa (%)
40
30
15
10
5

185. Matemática
c)
Modalidade
Futebol
Vôlei
Basquete
Natação
Outros
fa (%)
40
20
15
10
5
d)
Modalidade
Futebol
Vôlei
Basquete
Natação
Outros
fa (%)
40
30
15
20
5
Resposta
Alternativa “b”
03 Observe o gráfico a seguir resultante de uma pesquisa sobre os meios de transporte mais utilizado pela
população.
Construa uma tabela que represente este gráfico.
Sugestão de solução
Meio de transporte mais utilizado
Meio de transporte
Número de pessoas
Automóvel
750
Metrô
1200
Ônibus
1500
Moto
580
185

186. Matemática
Desafio
O gráfico a seguir representa a evolução de uma população ao longo dos anos, segundo os dados
estatísticos.
a) Qual o valor aproximado da população no ano de 1992?
b) Qual ou quais o(s) ano(s) em que a população foi igual a 100 milhões?
c) A partir de que ano a população passa a ser mais de 10 milhões?
d) Qual parece ser a evolução nos próximos anos?
e) Construa uma tabela que se relacione com os dados apresentados no gráfico.
Respostas
a) 99 milhões.
b) 1983, 1984,1985, 1986 e 1987.
c) 1994.
d) De crescimento
OBS: Sugerimos ao professor que, após os alunos realizarem as atividades, realize juntamente com eles
as interpretações do gráfico e tabelas, discutindo cada item.
186

187. Matemática
Aula 48
Relacionar tabelas com gráficos
Objetivo geral
Fazer a relação e a interpretação entre os dados da
tabela com os dados dos gráficos.
Orientação para análise dos gráficos e tabelas
 Leia com atenção o que é perguntado no
problema, confronte os questionamentos com os
dados verificados na tabela e nos gráficos.
O que devo aprender
nesta aula
u Construir tabelas e gráficos de
frequências de dados estatísticos.
u Traduzir informações contidas em
tabelas e gráficos diversos.
Atividades
01 O Ranking Mundial de Clubes é um ranking divulgado mensalmente pela Federação Internacional de His-
tória e Estatísticas do Futebol - IFFHS. Não tem qualquer vínculo com a FIFA. Esse ranking, criado em 1991, leva em
consideração os resultados de todos os clubes nos últimos 365 dias.
A tabela a seguir apresenta a pontuação dos 10 (dez) primeiros Clubes brasileiros no ranking.
Posição
8
15
16
36
47
52
56
95
99
125
Clube
Corinthians
Santos
Fluminense
São Paulo
Grêmio
Vasco da Gama
Internacional
Flamengo
Palmeiras
Curitiba
Pontos
240,0
211,0
210,0
184,0
172,0
166,0
162,0
125,0
124,0
112,0
Fonte: Disponível em: <http://pt.wikipedia.org/wiki/Ranking_Mundial_de_Clubes_da_
IFFHS#Os_30_primeiros_no_ranking>. Acesso em: 09 de dez. 2012. Última atualização:
6 de dezembro de 2012
187

188. Matemática
Qual é o gráfico que representa o ranking dos clubes brasileiros nessa data?
a)
b)
c)
188

189. Matemática
d)
Resposta
Alternativa “d”
02 Ainda sobre o Ranking Mundial de Clubes, com dados retirados no mesmo emdereço eletrônico, a tabela a seguir
apresenta os 10 maiores times de todos os tempos.
Posição
1
2
3
5
6
7
8
9
10
Clube
Barcelona
Manchester United
Real Madrid
Juventus
Milan
Internazionale
Bayern de Munique
Arsenal
River Plate
Chelsea
A alternativa que representa os dados conforme colocados na tabela é:
a)
189

190. Matemática
b)
c)
d)
Resposta
Alternativa “b”
03 Jogos Olímpicos - A cada quatro anos, atletas de centenas de países se reúnem num país sede para disputarem um conjunto de modalidades esportivas. A própria bandeira olímpica representa essa união de povos e raças, pois
190

191. Matemática
é formada por cinco anéis entrelaçados, representando os cinco continentes e suas cores. A paz, a amizade e o bom
relacionamento entre os povos e o espírito olímpico são os princípios dos jogos olímpicos.
O Brasil é o 38º com 17 medalhas de ouro e em 2016, as Olimpíadas ocorrerão na cidade do Rio de Janeiro.
Os dez países com mais medalhas de ouro Olímpicas
País
Estados Unidos
União Soviética
Reino Unido
Alemanha
França
Itália
China
Hungria
Alemanha Oriental
Suécia
Medalhas
932
395
208
192
191
190
163
159
153
142
Fonte: Disponível em: <http://rankz.wordpress.com/2008/07/24/os-dez-paises-com-mais-medalhas-olimpicas/>. Acesso em: 09 de dez. 2012.
Qual dos gráficos a seguir representa os dez países com maior número de medalhas Olímpicas?
a)
b)
191

192. Matemática
c)
d)
Sugestão de solução: Alternativa “d”
192

193. Matemática
Desafio
Paraolimpíadas - As pessoas com deficiências tradicionalmente discriminadas pela sociedade, e desmotivados pela sua própria condição existencial, têm nas paraolimpíadas uma oportunidade para elevar sua
autoestima, direta ou indiretamente, além de provar para todos o seu valor como atleta e cidadão. Desde
a XVI Olimpíada, realizada em Roma, em 1960 , imediatamente após as Olimpíadas, e nas mesmas instalações são realizados as Paraolimpíadas ou os Jogos Paraolímpicos. (http://www.coladaweb.com/educacao-fisica/
paraolimpiadas)
Veja aqui o quadro de medalhas das Paraolimpíadas 2012. O Brasil terminou em sétimo lugar!
País
Total
China
231
Rússia
102
Grã Bretanha
120
Ucrânia
84
Austrália
85
E.U.A
98
Brasil
43
Alemanha
66
Polônia
36
Holanda
39
Fonte: Disponível em: <http://www.esportesemanal.
com.br/quadro-de-medalhas-paraolimpiadas.aspx>.
Acesso em: 09 de dez. 2012.
a)
O gráfico que representa os dados da tabela é:
193

194. Matemática
b)
c)
d)
Sugestão de solução:
Alternativa “d”
194

195. Matemática
Aula 49
Conclusões com base na leitura
de tabelas
Objetivo geral
Ler, interpretar e realizar conclusões a partir
da observação dos dados encontrados em tabelas.
u Construir tabelas e gráficos de
frequências de dados estatísticos;
u Elaborar, oralmente ou por escrito,
Atividades
conclusões com base em leitura,
interpretação e análise de informações
apresentadas em tabelas e gráficos.
01 A tabela a seguir apresenta os 10 (dez) cursos mais
concorridos oferecidos pela Universidade Estadual de Goiás UEG, no Processo Seletivo 2013/1.
Cursos
Agronomia
Arquitetura e Urbanismo
Educação Física
Enfermagem
Engenharia Agrícola
Engenharia Civil
Farmácia
Fisioterapia
Química Industrial
Zootecnia
O que devo aprender nesta aula
Cidade
Ipameri
Anápolis
Goiânia
Ceres
Anápolis
Anápolis
Anápolis
Goiânia
Anápolis
São Luís de Montes Belos
* número de candidatos por vaga
Fonte: Disponível em: <http://www.vestibular.ueg.br/>. Acesso em: 10 de dez. 2012.
u Traduzir informações contidas em
tabelas e gráficos diversos.
Concorrência*
12,71
30,29
21,88
11,96
12,17
85,79
21,67
39,92
18,50
11,17
Considerando os dados é correto afirmar:
a) O curso de Engenharia civil foi o mais procurado pelos alunos.
b) Enfermagem, oferecido na cidade de Ceres foi o segundo curso mais procurado.
c) Os cursos oferecidos na cidade de Goiânia estão colocados na segunda e na quinta posição dos mais procurados nesse processo seletivo.
d) Dos cursos oferecidos na cidade de Anápolis, Química Industrial foi o menos concorrido.
Sugestão de solução
Alternativa “a”.
195

196. Matemática
Justificando as demais alternativas
b) Enfermagem foi o nono curso mais procurado.
c) Educação Física = quarta posição; Fisioterapia = segunda posição.
d) Engenharia Agrícola o menos concorrido na cidade de Anápolis.
02 A tabela a seguir apresenta os 10 (dez) cursos mais concorridos oferecidos pela Universidade Federal de Goiás
- UFG, no Vestibular 2013/1, para a cidade de Goiânia.
Cursos
Concorrência
Arquitetura e Urbanismo
24,60
Direito*
29,25
Direito**
24,33
Engenharia Civil
41,81
Engenharia Mecânica
16,53
Engenharia Química
16,75
Medicina
64,48
Psicologia
22,75
Odontologia
22,56
Relações Internacionais
13,59
* Conforme documento.
Fonte: Disponível em: < http://www.vestibular.ufg.br/2013/ps2013_1/site/sistema/resultado/candidato_vaga_PS2013_1.pdf/>. Acesso em: 10 de dez. 2012.
Observando a tabela responda:
a) Qual o Curso, dentre os apresentados, mais procurado e o menos procurado pelos candidatos nesse vestibular da UFG?
b) Os cursos que ocupam a quarta e quinta posição dos mais procurados são:
Sugestão de solução
a) Mais procurado = Medicina
Menos procurado = Relações internacionais.
b) Quarto = Arquitetura e Urbanismo
Quinto = Direito**
196

197. Matemática
03 Observe a tabela a seguir. Ela apresenta os 10 (dez) primeiros Clubes brasileiros no Ranking Mundial de Clubes.
Posição
Clube
Pontos
8
Corinthians
240,0
15
Santos
211,0
16
Fluminense
210,0
36
São Paulo
184,0
47
Grêmio
172,0
52
Vasco da Gama
166,0
56
Internacional
162,0
95
Flamengo
125,0
99
Palmeiras
124,0
125
Curitiba
112,0
Última atualização: 6 de dezembro de 2012
Fonte: Disponível em: < http://pt.wikipedia.org/wiki/Ranking_Mundial_de_Clubes_da_
IFFHS#Os_30_primeiros_no_ranking>. Acesso em: 09 de dez. 2012.
De acordo com os dados é correto afirmar que
a) São Paulo ocupa a quinta posição no Ranking Mundial de Clubes.
b) Considerando que o Brasil só classifica para próxima fase os dois clubes mais bem pontuados, esses clubes
são o do Corinthians e o do Santos.
c) Curitiba esta na décima posição com 112 (cento e doze) pontos.
Sugestão de solução
Alternativa correta = item “b”
Justificando as demais alternativas
a) São Paulo ocupa a trigésima sexta posição.
c) Curitiba = 125ª posição com com 112 (cento e doze) pontos.
197

198. Matemática
Desafio
Considere as tabelas das atividades 01 e 02.
Cursos mais concorridos oferecidos pela UEG,
no Processo Seletivo 2013/1.
Cursos
Cidade
Concorrência
Agronomia
Ipameri
12,71
Arquitetura e
Anápolis
30,29
Urbanismo
Educação Física
Goiânia
21,88
Enfermagem
Ceres
11,96
Engenharia Agrícola Anápolis
12,17
Engenharia Civil
Anápolis
85,79
Farmácia
Anápolis
21,67
Fisioterapia
Goiânia
39,92
Química Industrial
Anápolis
18,50
São Luís de
Zootecnia
11,17
Montes Belos
Cursos mais concorridos oferecidos pela
UFG, no Vestibular 2013/1, para a cidade de
Goiânia.
Cursos
Concorrência
Arquitetura e Urbanismo
24,60
Direito*
29,25
Direito*
24,33
Engenharia Civil
41,81
Engenharia Mecânica
16,53
Engenharia Química
16,75
Medicina
64,48
Psicologia
22,75
Odontologia
22,56
Relações Internacionais
13,59
Com base nos dados das duas tabelas, responda:
a) Qual o curso mais concorrido nas duas Universidades.
b) A concorrência do curso de Arquitetura e Urbanismo das duas Universidades.
c) Cursos, dentre os apresentados oferecidos nas duas Universidades.
d) O curso mais concorrido na UEG e o menos concorrido na UFG.
Sugestão de solução:
a) UEG – Engenharia Civil e UFG – Medicina
b) Arquitetura e Urbanismo na UEG – 30,29
Arquitetura e Urbanismo na UFG – 24,60
c) Arquitetura e Urbanismo e Engenharia Civil
d) Mais concorrido UEG - Engenharia Civil
Menos concorrido UFG - Relações internacionais.
198