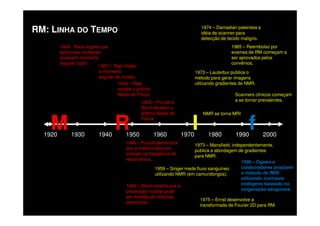
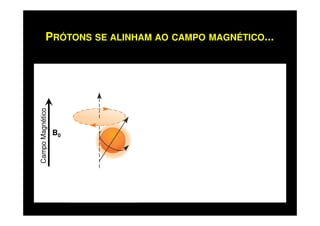
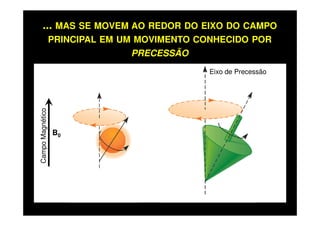
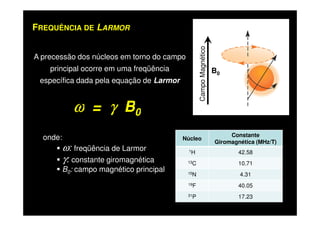
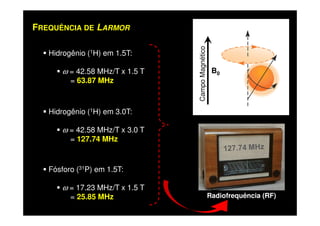
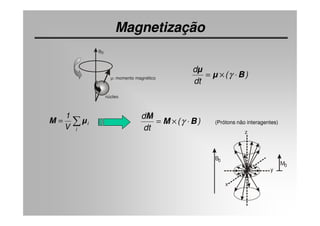
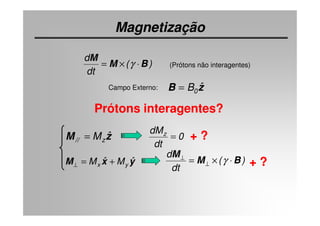
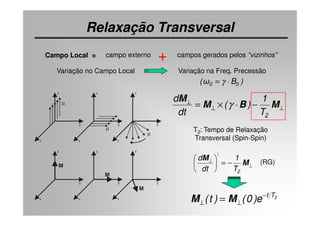
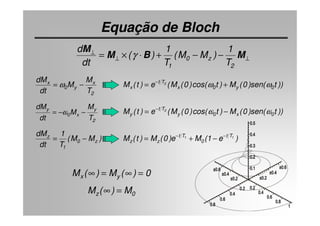
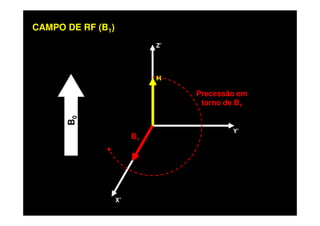
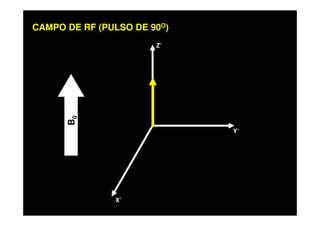
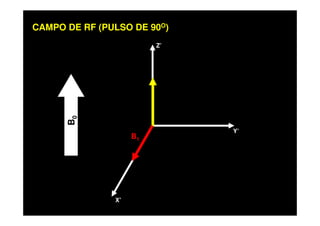
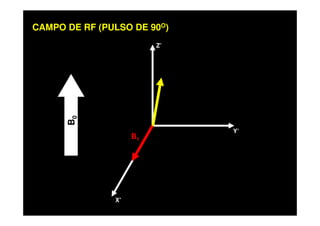
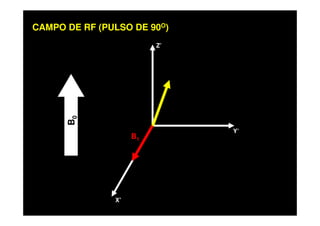
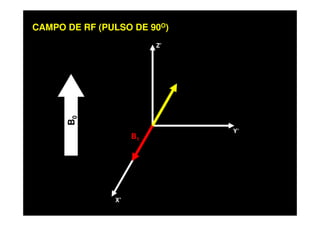
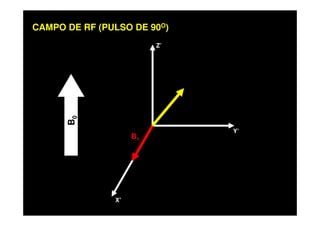
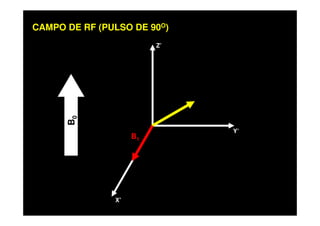
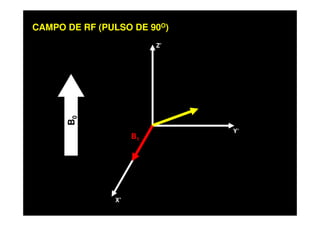
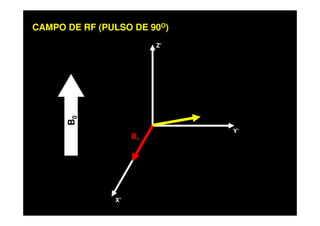
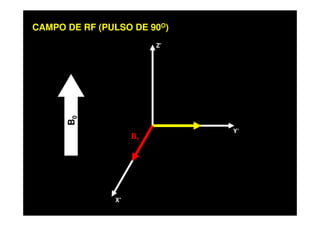
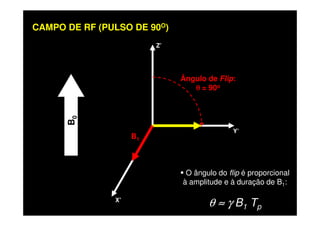
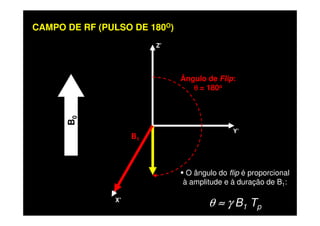
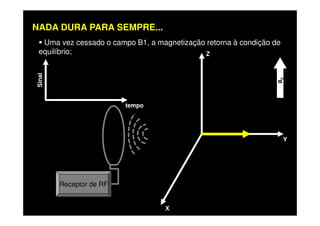
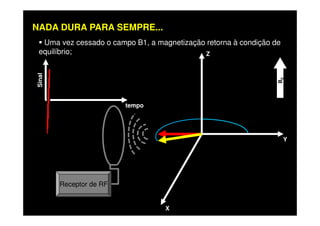
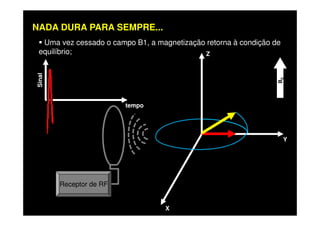
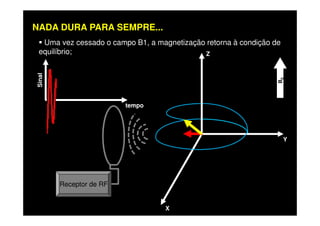
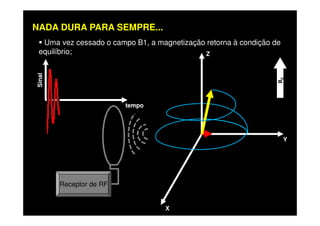
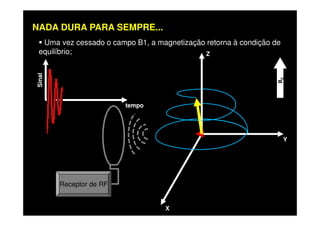
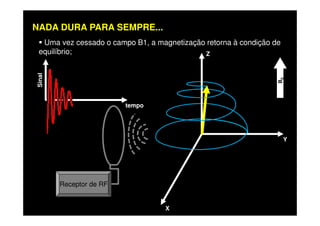
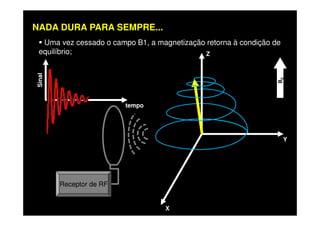
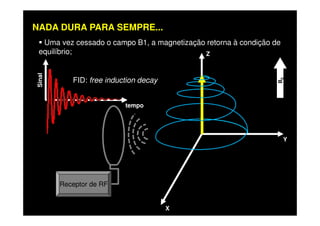
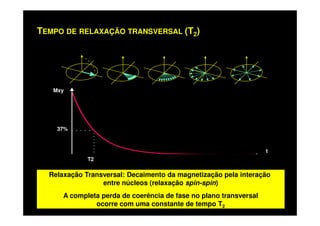
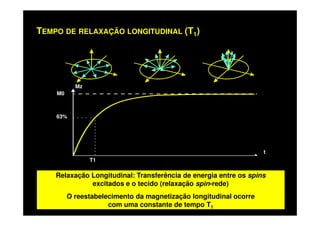
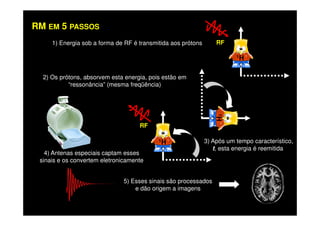
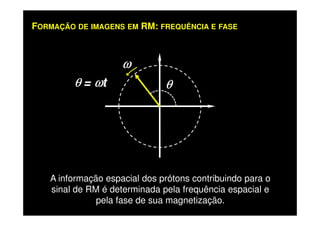
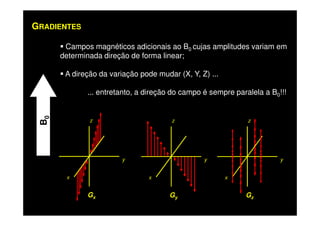
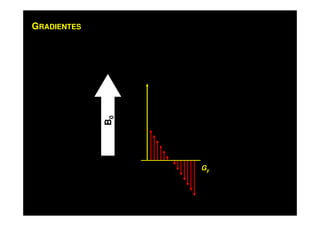
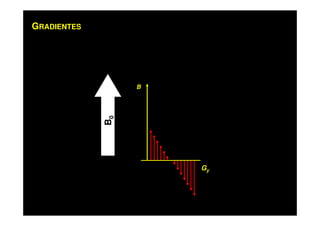
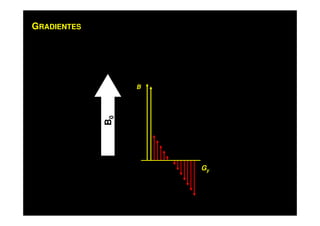
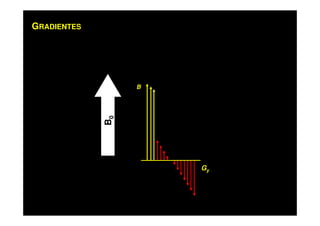
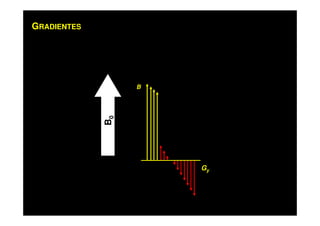
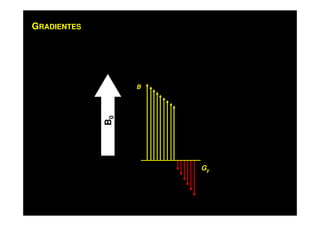
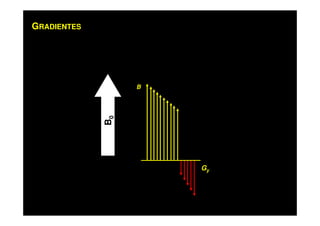
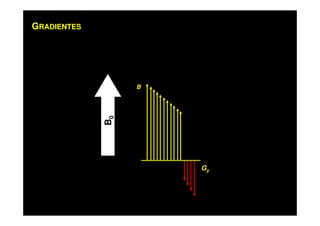
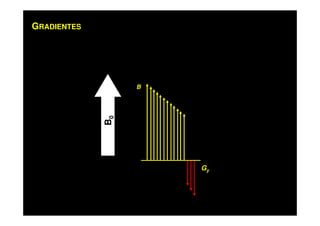
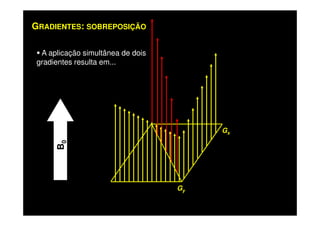
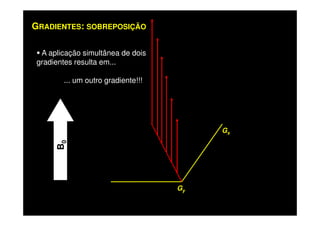
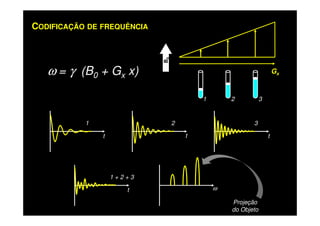
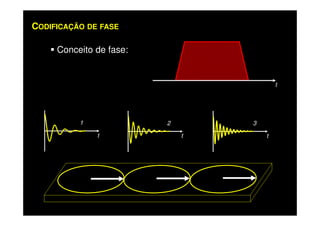
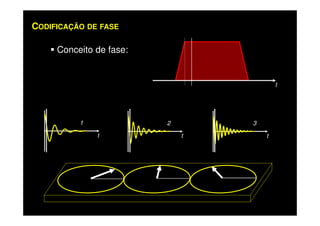
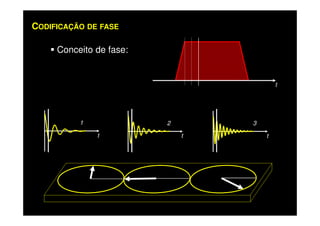
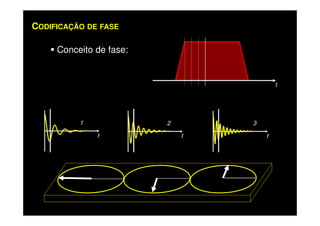
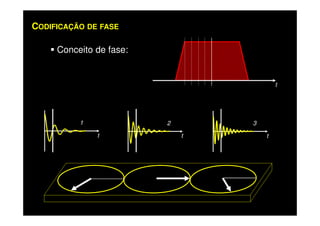
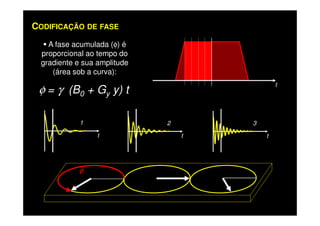
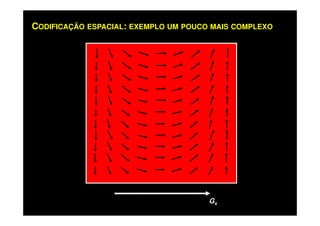
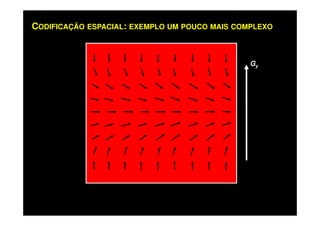
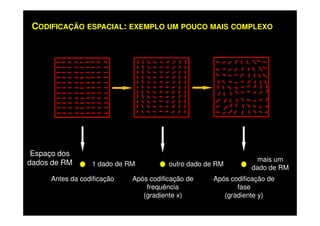
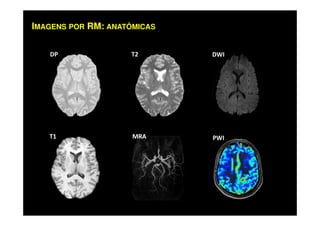
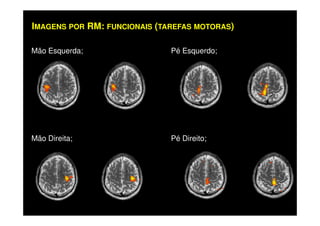
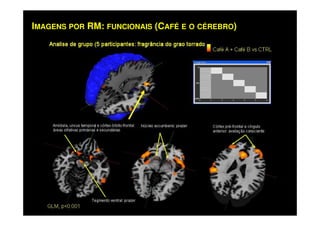
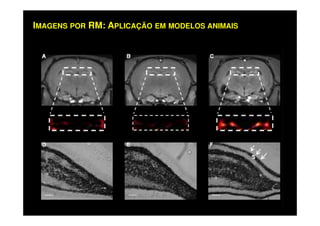
O documento discute os princípios da ressonância magnética (RM) e sua linha do tempo histórica. A RM utiliza campos magnéticos e ondas de rádio para gerar imagens anatômicas de alta qualidade sem o uso de radiação ionizante. O documento explica conceitos-chave como magnetização nuclear, relaxação spin-rede e spin-spin, frequência de Larmor, pulsos de rádiofrequência e a equação de Bloch.

1. Centro de Imagens e Espectroscopia
In Vivo por Ressonância Magnética
UNIVERSIDADE
DE SÃO PAULO
Instituto de Física de São Carlos
19/07/2012paiva@ifsc.usp.br
Imagens por Ressonância Magnética:
Princípios e Aplicações
Fernando F. Paiva

2. 1924 - Pauli sugere que
partículas nucleares
possuem momento
angular (spin).
1937 – Rabi mede
o momento
angular do núcleo.
1944 – Rabi
recebe o prêmio
Nobel de Física.
1952 – Purcell e
Bloch dividem o
prêmio Nobel de
M R
1974 – Damadian patenteia a
idéia de scanner para
detecção de tecido maligno.
1973 – Lauterbur publica o
método para gerar imagens
utilizando gradientes de NMR.
NMR se torna MRI
Scanners clínicos começam
a se tornar prevalentes.
1985 – Reembolso por
exames de RM começam a
ser aprovados pelos
convênios.
I f
RM: LINHA DO TEMPO
1920 1930 1940 1950 1960 1970 1980 1990 2000
1946 – Purcell demonstra
que a matéria absorve
energia na freqüência de
ressonância.
1946 – Bloch mostra que a
precessão nuclear pode
ser medida por bobinas
detectoras.
prêmio Nobel de
Física.
M R
1959 – Singer mede fluxo sanguíneo
utilizando NMR (em camundongos).
1973 – Mansfield, independentemente,
publica a abordagem de gradientes
para NMR.
1975 – Ernst desenvolve a
transformada de Fourier 2D para RM.
NMR se torna MRI
I
1990 – Ogawa e
colaboradores propõem
o método de fMRI
utilizando contraste
endógeno baseado na
oxigenação sanguínea.
f

3. A primeira tentativa de
obter uma imagem em
humanos. Dr. Raymond
Damadian foi o primeiro
paciente. Dadas as
MARÇO DE 1977
paciente. Dadas as
dúvidas sobre os
resultados, ele utilizou um
monitor cardíaco e um de
pressão.

4. A primeira tentativa bem sucedida de se obter uma imagem de
RM humanos. Dr. Lawrence Minkoff foi o voluntário.
JULHO DE 1977

5. A primeira imagem de RM obtida em humanos

6. ... 35 anos depois

7. A carga elétrica na
superfície do próton
cria um pequeno loop
de corrente, o que dá
origem ao momento
magnético ( );
A rotação do próton dá
origem ao momento
angular (J);
Ambos e J são
PROPRIEDADES DO NÚCLEO ATÔMICO
Ambos e J são
representados por
vetores que apontam ao
longo do eixo de rotação
e cuja direção pode ser
determinada pela regra
da mão direita;
Um núcleo pode ser observado por RM se tem momento angular e
magnético. Tal núcleo possui um número ímpar de prótons ou de nêutrons.

8. Na ausência de um
campo magnético
intenso, os spins ficam
randomicamente
PRÓTONS NA AUSÊNCIA DE CAMPO MAGNÉTICO
randomicamente
orientados.
Neste caso, a
magnetização (M) do
sistema é nula.

9. CampoMagnético
PRÓTONS SE ALINHAM AO CAMPO MAGNÉTICO...CampoMagnético
B0

10. Eixo de Precessão
CampoMagnético
... MAS SE MOVEM AO REDOR DO EIXO DO CAMPO
PRINCIPAL EM UM MOVIMENTO CONHECIDO POR
PRECESSÃO
CampoMagnético
B0

11. A precessão dos núcleos em torno do campo
principal ocorre em uma freqüência
específica dada pela equação de Larmor
ωωωω = γγγγ B0
FREQUÊNCIA DE LARMOR
CampoMagnético
B0
ωωωω = γγγγ B0
onde:
ω: freqüência de Larmor
γ: constante giromagnética
B0: campo magnético principal
Núcleo
Constante
Giromagnética (MHz/T)
1H 42.58
13C 10.71
15N 4.31
19F 40.05
31P 17.23

12. Hidrogênio (1H) em 1.5T:
ω = 42.58 MHz/T x 1.5 T
= 63.87 MHz
FREQUÊNCIA DE LARMOR
Hidrogênio (1H) em 3.0T:
CampoMagnético
B0
Núcleo
Constante
Giromagnética (MHz/T)
1H 42.58
13C 10.71
15N 4.31
19F 40.05
31P 17.23
Hidrogênio ( H) em 3.0T:
ω = 42.58 MHz/T x 3.0 T
= 127.74 MHz
Fósforo (31P) em 1.5T:
ω = 17.23 MHz/T x 1.5 T
= 25.85 MHz

13. Hidrogênio (1H) em 1.5T:
ω = 42.58 MHz/T x 1.5 T
= 63.87 MHz
FREQUÊNCIA DE LARMOR
Hidrogênio (1H) em 3.0T:
CampoMagnético
B0
Hidrogênio ( H) em 3.0T:
ω = 42.58 MHz/T x 3.0 T
= 127.74 MHz
Fósforo (31P) em 1.5T:
ω = 17.23 MHz/T x 1.5 T
= 25.85 MHz Radiofrequência (RF)

14. MagnetizaçãoMagnetização
núcleo
µ: momento magnético
B0
)(
dt
d
B⋅×= γ
dM1
)(
dt
d
BM
M
⋅×= γ (Prótons não interagentes)
x
y
z
B0
M0
∑=
i
i
V
1
M

15. MagnetizaçãoMagnetização
Prótons interagentes?Prótons interagentes?
)(
dt
d
BM
M
⋅×= γ (Prótons não interagentes)
zB ˆB0=Campo Externo:
yxM ˆMˆM yx +=⊥
zM ˆMz// = 0
dt
dMz
=
)(
dt
d
BM
M
⋅×= ⊥
⊥
γ
Prótons interagentes?Prótons interagentes?
+ ?+ ?
+ ?+ ?

16. Relaxação LongitudinalRelaxação Longitudinal
Interação dos prótons com a rede: )MM(
dt
dM
z0
z
−= ??
1T
1
Determinado Empiricamente
T1: Tempo de Relaxação Longitudinal (Spin-Rede)
)e1(Me)t(M)t(M 1010 T)tt(T)tt( −−−−
−+=
Tecido T1 (ms) T2 (ms)
matéria cinzenta 950 100
matéria branca 600 80
músculo 900 50
fluido cérebro-espinhal 4500 2200
gordura 250 60
sangue 1200 100-200
Valores típicos de tempos de relaxação, T1 e T2, de hidrogênio em diferentes
tecidos humanos medidos em 1.5T e 37ºC
)e1(Me)t(M)t(M 1010 T)tt(
0
T)tt(
0zz
−−−−
−+=

17. Relaxação TransversalRelaxação Transversal
Campo Local =Campo Local = campo externo campos gerados pelos “vizinhos”+
µ
z z z
Variação no Campo Local
)Bω( 00 ⋅= γ
Variação na Freq. Precessão
⊥⊥
⊥
−⋅×= MBM
M
2T
1
)(
dt
d
γ
M
M
M
µ
µ
yyy
y y y
zzz
xxx
x x x
2Tdt
T2: Tempo de Relaxação
Transversal (Spin-Spin)
⊥
⊥
−=





M
M
2
T
1
dt
d
(RG)
2Tt
e)0()t( −
⊥⊥ = MM

18. Equação de BlochEquação de Bloch
⊥⊥
⊥
−−+⋅×= MBM
M
2
z0
1 T
1
)MM(
T
1
)(
dt
d
γ
2
x
y0
x
T
M
M
dt
dM
−= ω
y
x0
y M
M
dM
−−= ω
))t(sen)0(M)tcos()0(M(e)t(M 0y0x
Tt
x
2
ωω += −
))t(sen)0(M)tcos()0(M(e)t(M 0x0y
Tt
y
2
ωω −= −
)MM(
T
1
dt
dM
z0
1
z
−=
2
x0
T
M
dt
−−= ω
)e1(Me)0(M)t(M 11 Tt
0
Tt
zz
−−
−+=
))t(sen)0(M)tcos()0(M(e)t(M 0x0yy ωω −=
0)(M)(M yx =∞=∞
0z M)(M =∞

19. Z’
M
Precessão em
torno de B1
CAMPO DE RF (B1)
X’
Y’
B0
B1

20. CAMPO DE RF (PULSO DE 90O)
Z’
X’
Y’
B0

21. CAMPO DE RF (PULSO DE 90O)
Z’
X’
Y’
B0
B1

22. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

23. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

24. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

25. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

26. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

27. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

28. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

29. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

30. Z’
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1

31. Z’
Ângulo de Flip:
θθθθ = 90o
CAMPO DE RF (PULSO DE 90O)
X’
Y’
B0
B1
O ângulo do flip é proporcional
à amplitude e à duração de B1:
θ ≈≈≈≈ γ B1 Tp

32. Z’
Ângulo de Flip:
θθθθ = 180o
CAMPO DE RF (PULSO DE 180O)
X’
Y’
B0
B1
O ângulo do flip é proporcional
à amplitude e à duração de B1:
θ ≈≈≈≈ γ B1 Tp

33. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
NADA DURA PARA SEMPRE...
tempo
Sinal
X
Y
Receptor de RF

34. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
tempo
Sinal
NADA DURA PARA SEMPRE...
X
Y
Receptor de RF

35. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
tempo
Sinal
NADA DURA PARA SEMPRE...
X
Y
Receptor de RF

36. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
tempo
Sinal
NADA DURA PARA SEMPRE...
X
Y
Receptor de RF

37. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
tempo
Sinal
NADA DURA PARA SEMPRE...
X
Y
Receptor de RF

38. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
tempo
Sinal
NADA DURA PARA SEMPRE...
X
Y
Receptor de RF

39. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
tempo
Sinal
NADA DURA PARA SEMPRE...
X
Y
Receptor de RF

40. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
tempo
Sinal
NADA DURA PARA SEMPRE...
X
Y
Receptor de RF

41. Uma vez cessado o campo B1, a magnetização retorna à condição de
equilíbrio; Z
B0
tempo
Sinal
FID: free induction decay
NADA DURA PARA SEMPRE...
X
Y
Receptor de RF

42. TEMPO DE RELAXAÇÃO TRANSVERSAL (T2)
Mxy
37%
T2
t
Relaxação Transversal: Decaimento da magnetização pela interação
entre núcleos (relaxação spin-spin)
A completa perda de coerência de fase no plano transversal
ocorre com uma constante de tempo T2
Relaxação Transversal: Decaimento da magnetização pela interação
entre núcleos (relaxação spin-spin)
A completa perda de coerência de fase no plano transversal
ocorre com uma constante de tempo T2

43. TEMPO DE RELAXAÇÃO LONGITUDINAL (T1)
M0
Mz
Relaxação Longitudinal: Transferência de energia entre os spins
excitados e o tecido (relaxação spin-rede)
O reestabelecimento da magnetização longitudinal ocorre
com uma constante de tempo T1
Relaxação Longitudinal: Transferência de energia entre os spins
excitados e o tecido (relaxação spin-rede)
O reestabelecimento da magnetização longitudinal ocorre
com uma constante de tempo T1
t
63%
T1

44. 2) Os prótons, absorvem esta energia, pois estão em
“ressonância” (mesma freqüência)
1) Energia sob a forma de RF é transmitida aos prótons RF
1H
RM EM 5 PASSOS
5) Esses sinais são processados
e dão origem a imagens
4) Antenas especiais captam esses
sinais e os convertem eletronicamente
3) Após um tempo característico,
t, esta energia é reemitida
1H
RF
1H

45. FORMAÇÃO DE IMAGENS: CONCEITO
Definição da localização espacialDefinição da localização espacial
das fontes que contribuem para o
sinal detectado.

46. UM EXEMPLO SIMPLES
Entretanto, RM não utiliza mecanismos como projeção,
reflexão ou refração, comumente utilizados em técnicas
óticas de formação de imagens.

47. FORMAÇÃO DE IMAGENS EM RM: FREQUÊNCIA E FASE
θθθθ
ωωωω
θθθθ = ωωωωt
A informação espacial dos prótons contribuindo para o
sinal de RM é determinada pela frequência espacial e
pela fase de sua magnetização.

48. Campos magnéticos adicionais ao B0 cujas amplitudes variam em
determinada direção de forma linear;
A direção da variação pode mudar (X, Y, Z) ...
... entretanto, a direção do campo é sempre paralela a B0!!!
GRADIENTES
B0
x
y
z
Gx
x
y
z
Gy
x
y
z
Gz

49. GRADIENTES
B0

50. GRADIENTES
Gy
B0

51. GRADIENTES
B
Gy
B0

52. GRADIENTES
B
Gy
B0

53. GRADIENTES
B
Gy
B0

54. GRADIENTES
B
Gy
B0

55. GRADIENTES
B
Gy
B0

56. GRADIENTES
B
Gy
B0

57. GRADIENTES
B
Gy
B0

58. GRADIENTES
B
Gy
B0

59. GRADIENTES
B
Gy
B0

60. GRADIENTES
B
Gy
B0

61. GRADIENTES
B
Gy
B0

62. GRADIENTES
B
Gy
B0

63. GRADIENTES
B
Gy
B0

64. GRADIENTES
B
Gy
B0

65. GRADIENTES
B
Gy
B0

66. GRADIENTES: SOBREPOSIÇÃO
A aplicação simultânea de dois
gradientes resulta em...
Gy
B0
Gx

67. GRADIENTES: SOBREPOSIÇÃO
A aplicação simultânea de dois
gradientes resulta em...
Gy
B0
Gx

68. GRADIENTES: SOBREPOSIÇÃO
A aplicação simultânea de dois
gradientes resulta em...
... um outro gradiente!!!
Gy
B0
Gx

69. ω = γ (B0 + Gx x)
CODIFICAÇÃO DE FREQUÊNCIA
Gx
B0
1 2 3
1 2 3
ttt
1 + 2 + 3
t ω
Projeção
do Objeto

70. CODIFICAÇÃO DE FASE
Conceito de fase:
t
3
t
2
t
1
t

71. CODIFICAÇÃO DE FASE
Conceito de fase:
t
3
t
2
t
1
t

72. CODIFICAÇÃO DE FASE
Conceito de fase:
t
3
t
2
t
1
t

73. CODIFICAÇÃO DE FASE
Conceito de fase:
t
3
t
2
t
1
t

74. CODIFICAÇÃO DE FASE
Conceito de fase:
t
3
t
2
t
1
t

75. CODIFICAÇÃO DE FASE
t
A fase acumulada (φ) é
proporcional ao tempo do
gradiente e sua amplitude
(área sob a curva):
φ = γ (B0 + Gy y) t
3
t
2
t
1
t
φφφφ

76. CODIFICAÇÃO ESPACIAL: EXEMPLO UM POUCO MAIS COMPLEXO
Gx

77. CODIFICAÇÃO ESPACIAL: EXEMPLO UM POUCO MAIS COMPLEXO
Gy

78. CODIFICAÇÃO ESPACIAL: EXEMPLO UM POUCO MAIS COMPLEXO
Espaço dos
dados de RM 1 dado de RM
Após codificação de
frequência
(gradiente x)
Após codificação de
fase
(gradiente y)
Antes da codificação
outro dado de RM
mais um
dado de RM

79. ESPAÇO K
CodificaçãoCodificação
de fasede fase
Passo #1Passo #1
PontoPonto
temporal #1temporal #1
……..……..
……..……..
PontoPonto
temporal #2temporal #2
PontoPonto
temporal #3temporal #3
PontoPonto
temporal #1temporal #1
PontoPonto
temporal #2temporal #2
PontoPonto
temporal #3temporal #3
CodificaçãoCodificação
de fasede fase
Passo #2Passo #2
……..……..
……..……..
Codificação de Frequência
temporal #1temporal #1 temporal #2temporal #2 temporal #3temporal #3
PontoPonto
temporal #1temporal #1
PontoPonto
temporal #2temporal #2
PontoPonto
temporal #3temporal #3
Passo #2Passo #2
CodificaçãoCodificação
de fasede fase
Passo #3Passo #3

80. +Gy .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
Espaço Físico
Espaço K
ESPAÇO K
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
+Gx-Gx 0
-Gy
Cada um dos pontos no espaço k (mostrados em amarelo) consiste na
soma do sinal de RM de todos os voxels no espaço da imagem
quando submetidos ao campo de gradiente correspondente.

81. ESPAÇO K
Espaço k Imagem
FT (FT-1)

82. Imagem CompletaImagem Completa Imagem de IntensidadeImagem de Intensidade Imagem de DetalhesImagem de Detalhes
Espaço k CompletoEspaço k Completo Centro do Espaço kCentro do Espaço k Bordas do Espaço kBordas do Espaço k

83. O SISTEMA DE RM
Bobina
de RF
Paciente
Equipamento de RM
Bobinas de
Gradiente
Magneto
Scanner
Cama do
Paciente

84. RM: CAMPO MAGNÉTICO PRINCIPAL
Estado da arte:
Sistemas clínicos: 0.1T – 3.0T
Sistemas de animais: 2.0T – 11.7TSistemas de animais: 2.0T – 11.7T
Curiosidades:
1 Tesla = 10000 Gauss
Campo magnético da terra ~ 0.5 Gauss

85. IMAGENS POR RM: ANATÔMICAS
Clinicamente utilizada em uma grande variedade de especialidades
Mama
Crânio
Abdômen
Coluna
Coração
A qualidade da imagem é geralmente descrita em termos da relação
sinal ruído, da resolução espacial e do contraste.

86. DP T2 DWI
IMAGENS POR RM: ANATÔMICAS
T1 MRA PWI

87. Mão Esquerda; Pé Esquerdo;
IMAGENS POR RM: FUNCIONAIS (TAREFAS MOTORAS)
Mão Direita; Pé Direito;

88. IMAGENS POR RM: FUNCIONAIS (CAFÉ E O CÉREBRO)

89. IMAGENS POR RM: APLICAÇÃO EM MODELOS ANIMAIS

90. Centro de Imagens e Espectroscopia
In Vivo por Ressonância Magnética
UNIVERSIDADE
DE SÃO PAULO
Instituto de Física de São Carlos
Fernando F. Paiva paiva@ifsc.usp.br
OBRIGADO!!!