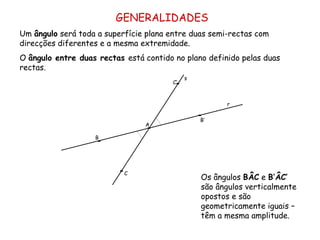
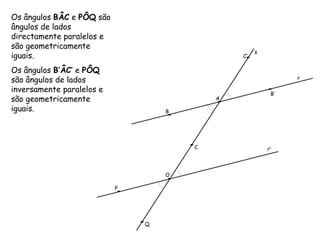
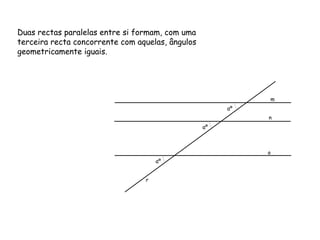
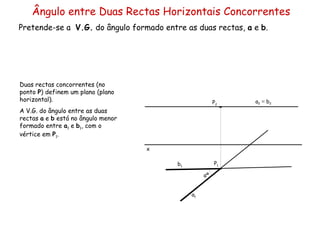
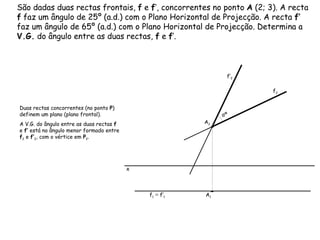
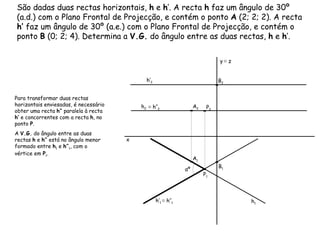
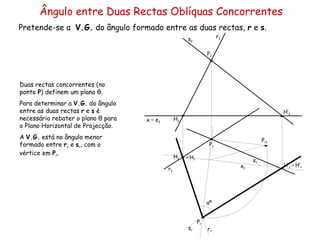
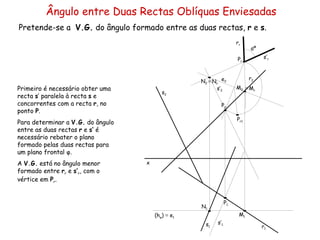
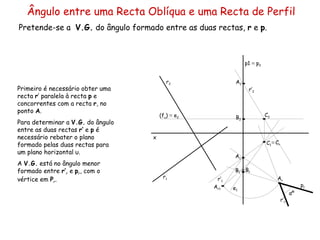
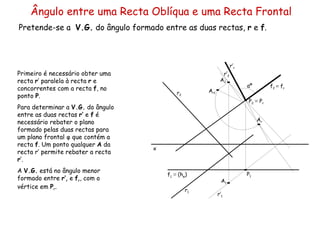
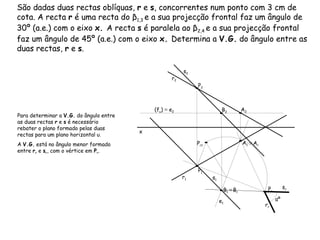
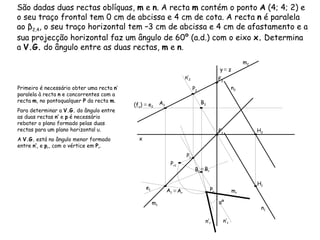
O documento discute vários tipos de ângulos entre duas retas em geometria descritiva. Explica como calcular a grandeza de ângulos entre retas paralelas, concorrentes, horizontais, frontais e oblíquas usando projeções auxiliares. Fornece exemplos passo a passo de como determinar a grandeza de ângulos entre diferentes combinações de retas.

1. GEOMETRIA DESCRITIVA A 11.º Ano Problemas Métricos Ângulos entre Duas Rectas © antónio de campos, 2010

2. GENERALIDADES Um ângulo será toda a superfície plana entre duas semi-rectas com direcções diferentes e a mesma extremidade. O ângulo entre duas rectas está contido no plano definido pelas duas rectas. s r A B B’ C C’ Os ângulos BÂC e B’ÂC’ são ângulos verticalmente opostos e são geometricamente iguais – têm a mesma amplitude.

3. s r A O ângulo entre duas rectas é sempre o menor ângulo por estas formado. O estdudo sobre ângulos trata da V.G. da sua amplitude, utilizando uma qualquer letra minúscula do alfabeto grego para representar o ângulo. αº αº

4. s r A B B’ C C’ r’ O P Q Os ângulos BÂC e PÔQ são ângulos de lados directamente paralelos e são geometricamente iguais. Os ângulos B’ÂC’ e PÔQ são ângulos de lados inversamente paralelos e são geometricamente iguais.

5. m n o r αº αº αº Duas rectas paralelas entre si formam, com uma terceira recta concorrente com aquelas, ângulos geometricamente iguais.

6. Ângulo entre Duas Rectas Horizontais Concorrentes Pretende-se a V.G. do ângulo formado entre as duas rectas, a e b . a 2 ≡ b 2 a 1 b 1 Duas rectas concorrentes (no ponto P ) definem um plano (plano horizontal). A V.G. do ângulo entre as duas rectas a e b está no ângulo menor formado entre a 1 e b 1 , com o vértice em P 1 . αº x P 1 P 2

7. Ângulo entre Duas Rectas Frontais Enviesadas Pretende-se a V.G. do ângulo formado entre as duas rectas, a e b . a 2 a 1 b 1 Para transformar duas rectas frontais enviesadas, é necessário obter uma recta b ’ paralela à recta b e concorrentes com a recta a , no ponto P . A V.G. do ângulo entre as duas rectas a e b’ está no ângulo menor formado entre a 2 e b’ 2 , com o vértice em P 2 . b 2 ≡ b’ 1 b’ 2 αº x P 1 P 2

8. São dadas duas rectas frontais, f e f ’, concorrentes no ponto A (2; 3). A recta f faz um ângulo de 25º (a.d.) com o Plano Horizontal de Projecção. A recta f’ faz um ângulo de 65º (a.d.) com o Plano Horizontal de Projecção. Determina a V.G. do ângulo entre as duas rectas, f e f ’. f 1 ≡ f’ 1 f 2 f’ 2 Duas rectas concorrentes (no ponto P ) definem um plano (plano frontal). A V.G. do ângulo entre as duas rectas f e f’ está no ângulo menor formado entre f 2 e f’ 2 , com o vértice em P 2 . αº x A 1 A 2

9. São dadas duas rectas horizontais, h e h ’. A recta h faz um ângulo de 30º (a.d.) com o Plano Frontal de Projecção, e contém o ponto A (2; 2; 2). A recta h’ faz um ângulo de 30º (a.e.) com o Plano Frontal de Projecção, e contém o ponto B (0; 2; 4). Determina a V.G. do ângulo entre as duas rectas, h e h ’. h 2 h 1 h’ 2 h’ 1 Para transformar duas rectas horizontais enviesadas, é necessário obter uma recta h’’ paralela à recta h’ e concorrentes com a recta h , no ponto P . A V.G. do ângulo entre as duas rectas h e h’’ está no ângulo menor formado entre h 1 e h’’ 1 , com o vértice em P 1 . ≡ h’’ 2 ≡ h’’ 1 αº x y ≡ z A 1 A 2 B 1 B 2 P 1 P 2

10. Ângulo entre Duas Rectas Oblíquas Concorrentes Pretende-se a V.G. do ângulo formado entre as duas rectas, r e s . r 1 r 2 s 2 s 1 Duas rectas concorrentes (no ponto P ) definem um plano θ. Para determinar a V.G. do ângulo entre as duas rectas r e s é necessário rebater o plano θ para o Plano Horizontal de Projecção. A V.G. está no ângulo menor formado entre r r e s r , com o vértice em P r . e 1 ≡ e 2 ≡ H r ≡ H’ r r r s r αº x P 1 P 2 H 1 H 2 H’ 1 H’ 2 P r1 P r

11. Ângulo entre Duas Rectas Oblíquas Enviesadas Pretende-se a V.G. do ângulo formado entre as duas rectas, r e s . r 2 s 2 s 1 r 1 Primeiro é necessário obter uma recta s ’ paralela à recta s e concorrentes com a recta r , no ponto P . Para determinar a V.G. do ângulo entre as duas rectas r e s’ é necessário rebater o plano formado pelas duas rectas para um plano frontal φ. A V.G. está no ângulo menor formado entre r r e s’ r , com o vértice em P r . s’ 1 s’ 2 (h φ ) ≡ e 1 e 2 ≡ M r ≡ N r αº s’ r r r x P 1 P 2 M 1 M 2 N 1 N 2 P r1 P r

12. Ângulo entre uma Recta Oblíqua e uma Recta de Perfil Pretende-se a V.G. do ângulo formado entre as duas rectas, r e p . p1 ≡ p 2 r 1 r 2 Primeiro é necessário obter uma recta r ’ paralela à recta p e concorrentes com a recta r , no ponto A . Para determinar a V.G. do ângulo entre as duas rectas r’ e p é necessário rebater o plano formado pelas duas rectas para um plano horizontal υ. A V.G. está no ângulo menor formado entre r’ r e p r , com o vértice em P r . r’ 1 r’ 2 (f υ ) ≡ e 2 ≡ B r ≡ C r e 1 p r r’ r αº x A 1 B 1 B 2 A 2 C 1 C 2 A r1 A r

13. Ângulo entre uma Recta Oblíqua e uma Recta Frontal Pretende-se a V.G. do ângulo formado entre as duas rectas, r e f . r 2 r 1 f 1 f 2 Primeiro é necessário obter uma recta r ’ paralela à recta r e concorrentes com a recta f , no ponto P . Para determinar a V.G. do ângulo entre as duas rectas r’ e f é necessário rebater o plano formado pelas duas rectas para um plano frontal φ que contém a recta f . Um ponto qualquer A da recta r’ permite rebater a recta r ’. A V.G. está no ângulo menor formado entre r’ r e f r , com o vértice em P r . r’ 1 r’ 2 ≡ (h φ ) ≡ f r ≡ P r r’ r αº x P 1 P 2 A 1 A 2 A r1 A r

14. São dadas duas rectas oblíquas, r e s , concorrentes num ponto com 3 cm de cota. A recta r é uma recta do β 1,3 e a sua projecção frontal faz um ângulo de 30º (a.e.) com o eixo x. A recta s é paralela ao β 2,4 e a sua projecção frontal faz um ângulo de 45º (a.e.) com o eixo x. Determina a V.G. do ângulo entre as duas rectas, r e s . r 2 r 1 s 2 s 1 Para determinar a V.G. do ângulo entre as duas rectas r e s é necessário rebater o plano formado pelas duas rectas para um plano horizontal υ. A V.G. está no ângulo menor formado entre r r e s r , com o vértice em P r . (f υ ) ≡ e 2 e 1 ≡ A r ≡ B r r r s r αº x P 1 P 2 A 1 A 2 B 1 B 2 P r1 P r

15. São dadas duas rectas oblíquas, m e n . A recta m contém o ponto A (4; 4; 2) e o seu traço frontal tem 0 cm de abcissa e 4 cm de cota. A recta n é paralela ao β 2,4 , o seu traço horizontal tem –3 cm de abcissa e 4 cm de afastamento e a sua projecção horizontal faz um ângulo de 60º (a.d.) com o eixo x. Determina a V.G. do ângulo entre as duas rectas, m e n . m 2 m 1 n 1 n 2 Primeiro é necessário obter uma recta n ’ paralela à recta n e concorrentes com a recta m , no pontoqualquer P da recta m . Para determinar a V.G. do ângulo entre as duas rectas n’ e p é necessário rebater o plano formado pelas duas rectas para um plano horizontal υ. A V.G. está no ângulo menor formado entre n’ r e p r , com o vértice em P r . n’ 1 n’ 2 (f υ ) ≡ e 2 e 1 ≡ A r ≡ B r m r n’ r αº x y ≡ z A 1 A 2 F 2 F 1 H 1 H 2 P 1 P 2 B 1 B 2 P r1 P r