O documento aborda a determinação de interseções entre retas e planos, o cálculo de ângulos entre direções de retas enviesadas, e a representação de sólidos geométricos, incluindo a construção de sombras projetadas. São apresentados dados específicos para resolver problemas de geometria descritiva, como a localização de pontos e a projeção de formas em diferentes planos. Além disso, inclui uma análise de um exame nacional de geometria com exemplos de aplicação dos conceitos discutidos.

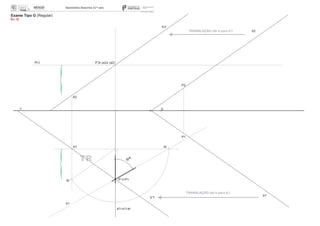
1. 1. Determine o ponto I, de interseção entre a reta a e o plano a.
Dados:
– a reta a é de perfil passante e contém o ponto A (0; –3; 5);
– o plano a está definido pelos pontos R (5; 0: 3) e S (8; 0; 0) e é perpendicular ao bissetor dos diedros
pares (b 2/4).
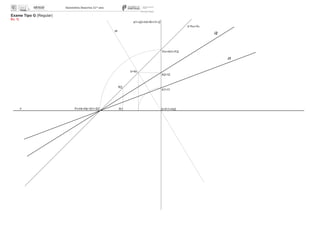
2. Determine a amplitude do ângulo (em projeções e V.G.) formado pelas direções das duas retas
enviesadas a e b.
Dados:
– a reta a é perpendicular ao plano frontal de projeção e tem 6cm de abcissa e 6cm de cota;
– a reta b pertence ao bissetor dos diedros ímpares (b 1/3), contém o ponto P (–3; 3; 3) e a sua projeção
horizontal faz um ângulo de 35º a.d. com o eixo x.
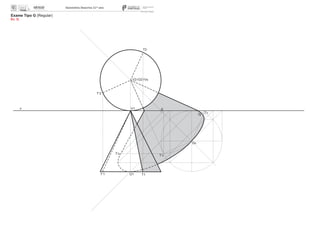
3. Represente pelas suas projeções um cone de revolução (reto), situado no 1º diedro, de acordo com os
dados abaixo apresentados.
Utilizando a direção luminosa convencional, determine a sombra própria do sólido e a sua sombra real
projetada nos planos de projeção.
Represente, a traço interrompido, as partes invisíveis da separatriz e do contorno da sombra projetada.
Identifique as áreas visíveis das sombras própria e projetada, preenchendo-as a tracejado ou com uma
mancha de grafite clara e uniforme.
(Se optar pelo tracejado, deverá fazê-lo com linhas paralelas ao eixo x, nas áreas de sombra própria, e com
linhas perpendiculares às respetivas projeções da direção luminosa, nas áreas de sombra projetada)
Dados:
– o vértice principal do sólido é o ponto V (4; 8; 4);
– a base do sólido está paralela ao plano frontal de projeção e tangente ao plano horizontal de projeção;
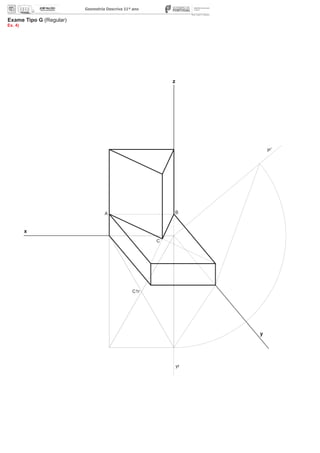
4. Construa uma representação axonométrica clinogonal cavaleira de um sólido composto por um
paralelepípedo e um prisma triangular regular (reto), sem sobreposição de sólidos.
Ponha em destaque, no desenho final, apenas o traçado das linhas visíveis do sólido resultante.
Dados:
Sistema axonométrico: axonometria clinogonal.
- a projeção axonométrica do eixo y faz um ângulo de 140º com a projeção do eixo z e um ângulo de 130º
com a projeção do eixo x;
- a inclinação das retas projetantes com o plano axonométrico é de 60º.
Aresta [AB]
– a aresta [AB] é comum a ambos os sólidos, sendo A(6; 0; 2) e B(0; 0; 2).
Prisma triangular regular (reto):
– as bases do prisma são triângulos equiláteros horizontais e a base [ABC] é a sua base de menor cota;
– o prisma mede 6cm de altura.
Paralelepípedo:
– as faces maiores do prisma são paralelas ao plano coordenado xy (horizontais);
– o vértice C do prisma triangular equilátero é o centro da face de maior cota do paralelepípedo.
EXAME NACIONAL GD TIPO – G (Regular)

2. x 0
Exame Tipo G (Regular)
Ex. 1)
ir ha fa
a1 a2 hq fq i1 i2
Ir Ar
Fi Hi Hir S1 S2
R2
R1
Fir Hi1 Fi2
Fi1 Hi2
A2 I2
ar
i2
A1 I1
i1

3. x 0
Exame Tipo G (Regular)
Ex. 2)
P’2 (e2) (a2)
a1 e1 ar
} A2
A1
Ar’
}
Ar
P’1 P’r
b2
b1
P2
P1
b’2
b’1
TR
b’r
TRANSLAÇÃO (de b para b’)
TRANSLAÇÃO (de b para b’)
(fa)
aº

4. x 0
Exame Tipo G (Regular)
Ex. 3)
V2 O2 Vs
T2
T’2
V1
O1 T1T’1
T’s
Ts
Tv
T’v
Ov

5. Exame Tipo G (Regular)
Ex. 4)
y
x
z
C1r
C
A B
yr
yr’