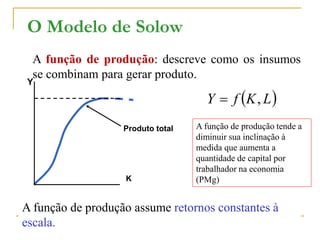
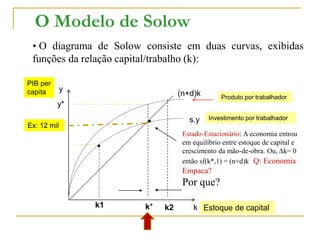
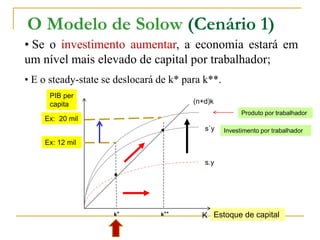
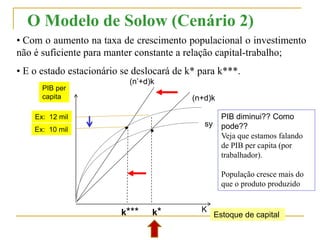
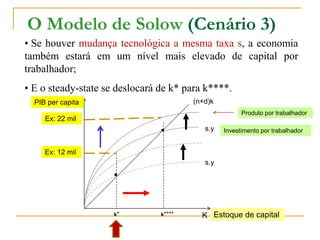
O documento descreve o Modelo de Solow de crescimento econômico, que explica como a poupança, o crescimento populacional e o progresso técnico afetam a taxa de crescimento do PIB ao longo do tempo. O modelo contém duas equações principais: a função de produção e a função de acumulação de capital. O modelo mostra que a economia tende a um estado estacionário de equilíbrio no longo prazo, onde o investimento iguala a depreciação do capital.

1. O Modelo de Solow
Alexandre Nunes de Almeida

2. O Modelo de Solow
 O modelo de crescimento econômico de SOLOW
(1956) explica como a poupança (capital), o aumento
da população e o progresso técnico influenciam a taxa
de crescimento do produto (PIB) no tempo.
 Assumimos que:
 Os países produzem e consomem apenas um único, e
homogêneo, produto;
 A tecnologia é dada (constante); mas podemos variar
e ver o que acontece
 Não há comércio internacional; T – G =0
 A taxa de participação da força de trabalho cresce a
uma taxa n igual ao crescimento da população

3. O Modelo de Solow
 O modelo de crescimento proposto por Solow
(1956) é construído em torno de duas equações
que definem:
 Uma função de produção: descreve como os
insumos (capital e trabalho) se combinam para
gerar uma unidade produto;
 Uma função de acumulação de capital

4. O Modelo de Solow
A função de produção: descreve como os insumos
se combinam para gerar produto.
A função de produção assume retornos constantes à
escala.
 LKfY ,
Produto total
K
Y
A função de produção tende a
diminuir sua inclinação à
medida que aumenta a
quantidade de capital por
trabalhador na economia
(PMg)

5. O Modelo de Solow
 Para simplificar, todas as variáveis da função de
produção são divididas pelo tamanho da força de
trabalho, L. Logo, teremos (cuidado com notação)
 Ou seja, a produção por trabalhador (per capita) é
função do capital por trabalhador também
 Simplificação para ilustrar o papel do capital no
crescimento econômico graficamente.
 Pode ser feito o inverso.
f(k,1)you 





1,
L
K
F=
L
Y

6. O Modelo de Solow
• A segunda equação fundamental do modelo de Solow descreve
a acumulação do capital ao longo do ano:
tt kdnysk  )(
• Δk = Variação anual do estoque da capital
• s.y = investimento (s=Savings=Investimento) que depende
da função de produção y=f(k,l). Se não produzir não tem
como poupar e portanto investir (0 < s < 1)
• d.k = depreciação do estoque de capital (Ex: 4% a.a.). (δ)
• nk = retorno do capital depende também da taxa de
crescimento da população (n). Por que? Afeta mão-de-
obra
∆𝑘 = 𝐾𝑡+1 − 𝐾𝑡

7. O Modelo de Solow
• A próxima figura ilustra a relação esperada entre
investimento, depreciação e investimento para
diferentes quantidades de k; Assim:
1. Quanto maior o estoque de capital maior também será
a depreciação. (NÃO TEM COMO EVITAR A
DEPRECIAÇAO SE VOCE ESTÁ USANDO)
2. Existe um nível de estoque de capital para o qual a
quantidade de investimento (parcela da produção sy) é
exatamente igual ao montante de depreciação (n+d)k.
3. É o chamado steady-state, ou estado estacionário do
capital ou também conhecido como equilíbrio de
longo prazo da economia

8. O Modelo de Solow
●
k2
s.y
(n+d)k
k*
Estado-Estacionário: A economia entrou
em equilíbrio entre estoque de capital e
crescimento da mão-de-obra. Ou, Δk= 0
então sf(k*,1) = (n+d)k Q: Economia
Empaca?
Por que?
k1
●
• O diagrama de Solow consiste em duas curvas, exibidas
funções da relação capital/trabalho (k):
k
y
Estoque de capital
y*
PIB per
capita
Produto por trabalhador
Investimento por trabalhador
Ex: 12 mil

9. O Modelo de Solow
 Note que:
 Se o estoque inicial de capital é inferior ao do
steady-state (estado estacionário), no ponto k1,
o investimento é maior que a taxa de
depreciação do capital.
 Ao longo do tempo, o estoque de capital cresce
juntamente com o produto, até aproximar-se do
estado estacionário (k*), ponto de equilíbrio

10. O Modelo de Solow
 Note que:
 Se o estoque de capital inicial é superior ao do
estado estacionário, no ponto k2, o investimento será
menor que a depreciação, o capital se deprecia mais
rapidamente do que é substituído
 Nesse caso, o estoque volta (Decisões) a aproximar-
se do steady-state, quando o investimento
novamente se iguala à depreciação.
 Atingido este ponto, o estoque de capital por
trabalhador (per capita) não aumenta nem diminui.

11. O Modelo de Solow
 Note que:
 A taxa de poupança não tem nenhum efeito sobre a taxa de
crescimento do produto por trabalhador. (Tem espaço continua
crescendo)
 Entretanto, a taxa de poupança determina o nível de produto por
trabalhador.(Até o ponto do retornos marginais decrescentes)
 Tudo o mais constante, portanto, os países com uma taxa de
poupança mais alta obterão um produto por trabalhador mais
elevado.
 Um aumento da taxa de poupança levará a um maior
crescimento do produto por trabalhador durante algum tempo,
mas não para sempre.

12. O Modelo de Solow (Cenário 1)
A. Imagine agora um AUMENTO na taxa de poupança
(savings, s que depende de f(k,1))
1. Ocorrerá um deslocamento para cima da curva s f(k).
2. Com o aumento da poupança, o investimento cresce,
porém, no início o estoque de capital por trabalhador
e a depreciação permanecem constantes.
3. O estoque de capital vai crescer gradualmente em
função do maior investimento, até que a economia
atinja um novo estado estacionário, k**.

13. O Modelo de Solow (Cenário 1)
 Imagine agora um AUMENTO na taxa de poupança
(Savings, S que depende de f(k))
1. Logo, nessa nova situação, o estoque de capital por
trabalhador e a produção serão maiores.
2. Assim, o modelo demonstra que no estado
estacionário a taxa de poupança é o principal
determinante do estoque de capital.
3. Portanto, com uma taxa de poupança maior o PIB
pode ser mais alto.
4. Essa diferença representa uma boa aproximação da
realidade ao comparar países pobres e ricos.

14. O Modelo de Solow (Cenário 1)
• Se o investimento aumentar, a economia estará em
um nível mais elevado de capital por trabalhador;
• E o steady-state se deslocará de k* para k**.
●
●
K
s.y
s`y
(n+d)k
k**k* Estoque de capital
Produto por trabalhador
Investimento por trabalhador
PIB per
capita
Ex: 12 mil
Ex: 20 mil

15. O Modelo de Solow (Cenário 2)
2. Vamos admitir agora que população e a força de
trabalho cresçam a uma taxa constante, n, MAS e
investimento (sy) permance constante.
1. O aumento do número de trabalhadores tende a diminuir o
estoque de capital por trabalhador, portanto tem efeito
contrário ao do investimento.
2. Como o número de trabalhadores está crescendo a uma
taxa n, o capital e o produto deveriam aumentar em ritmo
semelhante, mas não acontece.
3. Estamos falando de muita gente para pouca maquina
 Lembre-se da micro, produto marginal decrescente.

16. O Modelo de Solow (Cenário 2)
 Vamos admitir agora que população e a força de trabalho
cresçam a uma taxa constante, n.
4. Assim, esse crescimento demográfico oferece uma razão
adicional para explicar a desigualdade entre países, em
países que registram maiores taxas de crescimento da
população e da força de trabalho.
5. Crescimento do capital (junto com tecnologia) não
acompanha na mesma proporção.
6. A produção “encolhe”. Veja que estamos falando de
valores relativos. Por exemplo. PIB per capita.
População cresce mais do que o produto produzido

17. O Modelo de Solow (Cenário 2)
• Com o aumento na taxa de crescimento populacional o investimento
não é suficiente para manter constante a relação capital-trabalho;
• E o estado estacionário se deslocará de k* para k***.
K
sy
(n+d)k
k*k***
(n’+d)k
●●
Estoque de capital
PIB diminui?? Como
pode??
Veja que estamos falando
de PIB per capita (por
trabalhador).
População cresce mais do
que o produto produzido
PIB per
capita
Ex: 12 mil
Ex: 10 mil

18. O Modelo de Solow (Cenário 3)
• Se houver mudança tecnológica a mesma taxa s, a economia
também estará em um nível mais elevado de capital por
trabalhador;
• E o steady-state se deslocará de k* para k****.
●
●
K
s.y
s.y
(n+d)k
k****k* Estoque de capital
Produto por trabalhador
Investimento por trabalhador
PIB per capita
Ex: 12 mil
Ex: 22 mil