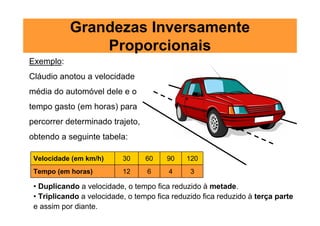
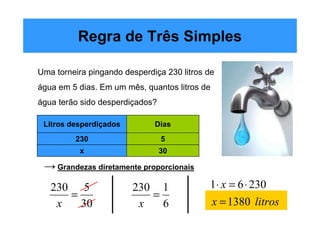
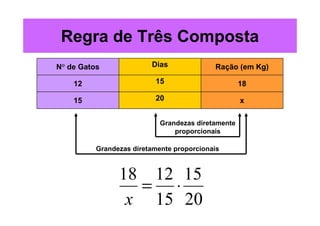
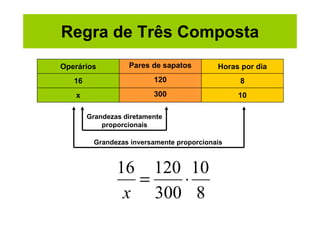
O documento apresenta exemplos de problemas resolvidos usando a regra de três, incluindo grandezas direta e inversamente proporcionais. Problemas envolvem preço de chocolates, tempo para realizar tarefas, quantidade de farinha para tortas, velocidade versus tempo para percorrer uma distância, desperdício de água, número de páginas em uma reimpressão, ração para gatos e produção de sapatos.

1. Aula 7 – 28/04/2011
Prof. Paulo Berndt

2. Regra de Três

3. Grandezas Proporcionais
Exemplo:
• O preço de uma barra de chocolate é → R$ 2,00
R$ 2,00.
• Se quisermos comprar duas barras de
→ R$ 4,00
chocolate, gastaremos R$ 4,00.
•Se quisermos comprar três barras de
chocolate, gastaremos R$ 6,00. → R$ 6,00
E assim por diante...
O número de chocolates comprados e o preço pago
por eles são grandezas diretamente proporcionais.

4. Grandezas Proporcionais
Exemplo:
• Em uma obra um operário realiza
→ 6 horas
determinada tarefa em 6 horas.
• Dois operários juntos, realizam a
→ 3 horas
mesma tarefa em 3 horas.
• Três operários juntos, realizam a
mesma tarefa em 2 horas. → 2 horas
E assim por diante...
O número de operários e o tempo gasto para realizar
a tarefa são grandezas inversamente proporcionais.

5. Grandezas Proporcionais
Será que a idade e a altura de uma pessoa são
grandezas proporcionais?
Vamos pensar um pouco:
Um homem de 80 anos tem
o quádruplo da altura de
um homem de 20 anos?
É claro que não!
Altura e idade são grandezas não proporcionais.

6. Grandezas Diretamente
Proporcionais
Exemplo: Para fazer uma torta de
morango, uma doceira utiliza 0,5 kg
de farinha. Quantos quilogramas de
farinha serão necessários para fazer
cinco tortas?
Vamos observar a tabela:
Número de tortas 1 2 3 4 5
Quantidade de farinha (em kg) 0,5 1 1,5 2 2,5
• Duplicando o n°de tortas, a quantidade de farinha fica duplicada.
• Triplicando o n°de tortas, a quantidade de farinha fica triplicada e
assim por diante.
Então, para fazer cinco tortas, serão necessários 2,5 kg de farinha.

7. Grandezas Inversamente
Proporcionais
Exemplo:
Cláudio anotou a velocidade
média do automóvel dele e o
tempo gasto (em horas) para
percorrer determinado trajeto,
obtendo a seguinte tabela:
Velocidade (em km/h) 30 60 90 120
Tempo (em horas) 12 6 4 3
• Duplicando a velocidade, o tempo fica reduzido à metade.
• Triplicando a velocidade, o tempo fica reduzido fica reduzido à terça parte
e assim por diante.

8. Regra de Três Simples
Uma torneira pingando desperdiça 230 litros de
água em 5 dias. Em um mês, quantos litros de
água terão sido desperdiçados?
Litros desperdiçados Dias
230 5
x 30
→ Grandezas diretamente proporcionais
230 5 230 1 1⋅ x = 6 ⋅ 230
= =
x 30 x 6 x = 1380 litros

9. Regra de Três Simples
Um livro de 270 páginas tem 45 linhas
por página. Ao reimprimi-lo, a editora
resolveu colocar 50 linhas por página.
Com quantas páginas ficou o livro?
N° de páginas N° de linhas por página
270 45
x 50
10 ⋅ x = 9 ⋅ 270
→ Grandezas inversamente proporcionais
2430
x=
270 50 270 10 10
= =
x 45 x 9 x = 243 páginas

10. Regra de Três Composta
Na alimentação de 12 gatos
durante 15 dias, consumiram-se
18 kg de ração. Para alimentar
15 gatos durante 20 dias,
quantos quilogramas de ração
serão necessários?
Gatos Dias Ração (em Kg)
12 15 18
15 20 x

11. Regra de Três Composta
N° de Gatos Dias Ração (em Kg)
12 15 18
15 20 x
Grandezas diretamente
proporcionais
Grandezas diretamente proporcionais
18 12 15
= ⋅
x 15 20

12. Regra de Três Composta
18 12 15 3 x = 5 ⋅18
= ⋅
x 15 20
3x = 90
18 12
= 90
x 20 x=
3
18 3
= x = 30 kg de ração
x 5

13. Regra de Três Composta
Numa fábrica de sapatos trabalham 16
operários que produzem em 8 horas de
serviço diário, 120 pares de calçados.
Desejando ampliar as instalações, o
dono da fábrica quer saber quantos
novos funcionários deverá contratar,
para que 300 pares de sapatos sejam
produzidos numa carga horária de 10
horas por dia.
Operários Pares de sapatos Horas por dia
16 120 8
x 300 10

14. Regra de Três Composta
Operários Pares de sapatos Horas por dia
16 120 8
x 300 10
Grandezas diretamente
proporcionais
Grandezas inversamente proporcionais
16 120 10
= ⋅
x 300 8

15. Regra de Três Composta
16 120 10 16 12
= ⋅ =
x 300 8 x 24
16 12 10 16 1
= ⋅ =
x 30 8 x 2
16 12 1 1 ⋅ x = 2 ⋅16
= ⋅
x 3 8 x = 32 operários
Como existem 16 operários na fábrica, o dono deve contratar
mais 16 funcionários, para que o número total seja 32.