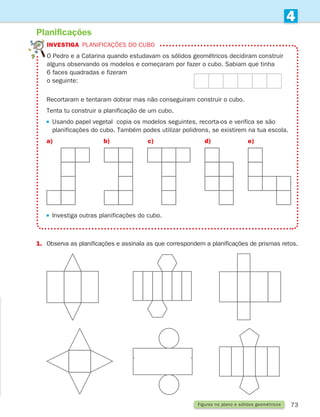
O documento apresenta um manual de matemática para o 4o ano de escolaridade. Inclui os nomes dos autores, da consultora pedagógica e da equipa técnica. Apresenta também os componentes do projeto, informações sobre a certificação do manual e os direitos de autor.

1. Dina Tavares, Fátima Gonçalves, Hugo Menino e Rita Cadima
Consultora pedagógica: Olga Seabra
Matemática
11,39 € IVA incluído
Conforme o novo
Acordo Ortográfico
da língua portuguesa
Matemática
Matemática
Componentes do projeto:
Manual do aluno
Fichas de avaliação (oferta ao aluno)
Caderno de atividades
Livromédia
4
ano
MANUAL CERTIFICADO pela Faculdade
de Ciências da Universidade de Lisboa,
nos termos da legislação em vigor
MANUAL CERTIFICADO
pela Faculdade de Ciências da Universidade de Lisboa
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
ano
C.
Produto
*213030202*
261287 CAPA.indd 1 13/02/17 12:09

2. O Projeto Desafios de Matemática
destina-se ao 4.o
ano de escolaridade
do 1.o
Ciclo do Ensino Básico.
EQUIPA TÉCNICA
Chefe de Equipa Técnica: Patrícia Boleto
Modelo Gráfico e Capa: Carla Julião
Ilustração da Capa: Nósnalinha
Ilustrações: Mafalda Duarte e Nósnalinha
Paginação: Christophe Marques, Leonor Ferreira,
Sérgio Alegria e Teresa Santos
Documentalista: Luísa Rocha
Revisão: Ana Abranches e Catarina Pereira
EDITOR
Armando Gonçalves
CONSULTORA PEDAGÓGICA
Olga Seabra — Mestre em Educação, na área de Supervisão
Pedagógica no Ensino da Matemática, pela Universidade do Minho
(Instituto de Educação e Psicologia). Docente do 2.º Ciclo do Ensino
Básico e formadora do novo Programa de Matemática
do Ensino Básico.
DIRETORA EDITORIAL
Sílvia Vasconcelos
A edição revista de acordo com as novas metas curriculares
é da responsabilidade de Dina Tavares, Fátima Gonçalves,
Hugo Menino e Rita Cadima.
© 2014
Rua Mário Castelhano, 40 – Queluz de Baixo
2734-502 Barcarena, Portugal
APOIO AO PROFESSOR
Tel.: 214 246 901
apoioaoprofessor@santillana.com
APOIO AO LIVREIRO
Tel.: 214 246 906
apoioaolivreiro@santillana.com
Internet: www.santillana.pt
Impressão e acabamento: Lidergraf
ISBN: 978-989-708-479-9
C. Produto: 213 030 202
2.a
Edição
4.a
Tiragem
Depósito Legal: 369968/14
A cópia ilegal viola os direitos dos autores.
Os prejudicados somos todos nós.
261287 CAPA.indd 2 13/02/17 12:10

3. Matemática
4
4
ano
261287 001-005.indd 1 30/05/14 17:48

4. 2
MODELO
DIDÁTICO
O teu manual organiza-se
em nove unidades.
Avaliação de diagnóstico
Atividades para recordares
os conteúdos do 3.º ano.
6
6
Avaliação de diagnóstico
Responde às questões no teu cadeRno diáRio.
7
7
Avaliação de diagnóstico
Responde às questões no teu cadeRno diáRio.
1. determina os números correspondentes às letras a, B, c, d, e e F.
Ficha n.o
1 Ficha n.o
2
1. desenha no teu caderno uma planta do teu quarto. compara a tua planta com as dos teus
colegas.
2. classifica cada uma das figuras geométricas quanto ao número de lados.
A
1200
B C D E F
400 500 600 700 800 900 1000 1100
A B C D E F G H
2. para cada uma das seguintes sequências determina uma possível regra de formação e,
de acordo com essa regra, escreve no teu caderno os cinco números seguintes.
a) 232 242 252
b) 405 425 445
c) 25 75 125
d) 927 827 727
3. copia as tabelas para o teu caderno e completa-as.
4 1 5 10
2 1 5 10
7 1 5 10
12 1 5 20
16 1 5 20
11 1 5 20
30 1 5 100
25 1 5 100
64 1 5 100
400 1 5 1000
750 1 5 1000
825 1 5 1000
4. observa a sequência de retângulos que se segue e determina uma possível
regra de formação.
Fig. 1 Fig. 2 Fig. 3 Fig. 4
a) de acordo com essa regra de formação, desenha no teu caderno o quinto retângulo
desta sequência.
b) de acordo com essa regra de formação, qual será a área, em quadrículas, do sexto
retângulo desta sequência? desenha-o no teu caderno.
c) copia para o teu caderno a tabela e completa-a, de acordo com essa regra de formação.
d) qual é a área da trigésima figura? explica o teu raciocínio.
número da figura 1 2 3 4 5 6 7 8 10 20
área em quadrículas 2 4 6 8
perímetro 6 8 10 12
3. observa os seguintes sólidos geométricos.
a) escreve no teu caderno o nome de cada um dos sólidos anteriores.
b) destes sólidos, indica:
um que tenha uma face triangular.
um que tenha uma face quadrada.
um que tenha uma face circular.
c) dos sólidos representados, indica:
um que tenha 8 vértices e 12 arestas;
um que tenha 6 vértices e 9 arestas;
um que tenha 5 vértices e 8 arestas.
4. calcula o resultado de cada uma das seguintes operações usando uma estratégia
de cálculo à tua escolha.
a) 345 1 230 b) 565 2 230 c) 231 1 149 d) 900 2 324
I
K
L
J
A
B
C
G
H
D
E
F
a B e
c d F G H
Abertura de unidade
Imagem, para explorar na sala
de aula, com uma situação
problemática que introduz
a unidade. Esta situação pode
desencadear uma discussão
em grupo que apela
à mobilização de conhecimentos
prévios dos alunos.
104 105
Calcular com números decimais
6
UNIDADE
Enquanto o pai abastece o carro, o Francisco e o irmão estão a olhar
para os preços dos combustíveis.
Qual é o combustível mais caro? E o mais barato?
Números racionais não negativos
a) Explica por palavras tuas a estratégia usada pelo Rodrigo.
b) Se cada um dos quatro ratinhos comesse 0,25 do queijo, quanto comeriam no total?
a) Quanto pagou cada uma das amigas pelo seu almoço?
b) Se a Joana almoçar todos os dias o mesmo, quanto gasta numa semana
(de segunda a sexta)?
2. O João e o Rodrigo estão a tentar resolver o seguinte problema:
«Quatro ratinhos comeram 0,15 de 1 queijo cada um. Quanto comeram no total?»
CalCuladora
Observa o desenho da página ao lado e, com a ajuda da calculadora, responde
às questões.
a) O rapaz abasteceu apenas 10 L de gasolina 95. Quanto pagou?
b) O camionista abasteceu 100 L de gasóleo. Quanto pagou?
c) O Sr. Gonçalves pagou 50 € de gasolina 98. Quantos litros comprou?
d) Se no dia seguinte todos os combustíveis sofressem um aumento de 0,05 €,
quais seriam os novos preços?
1. A Rita, a Joana e a Catarina foram almoçar juntas.
Eu calculei
mentalmente:
4 3 0,15
Pensei em 4 3 15
centésimas, dá 60
centésimas.
Ou seja, 0,60.
Eu calculei: 0,15
0,15
0,15
1 0,15
0,60
Rodrigo
João
Rita
Prato 6,60 €
Sumo 1,25 €
Doce 1,75 €
Joana
Prato 6,60 €
Água 0,50 €
Gelado 1,40 €
CataRina
Prato 6,60 €
Sumo 1,05 €
Fruta 1,55 €
Calculadora Atividade em que se
usa a calculadora como suporte na
exploração das relações numéricas.
Páginas de conteúdos
Os conteúdos são
explorados de diversas
formas e podes construir
a tua aprendizagem
página a página.
Área de exploração de um conceito
ou procedimento.
87
Números racionais não negativos
Frações em vários contextos
1. Na segunda-feira, o Pedro e mais quatro amigos dividiram, em partes iguais, uma piza
ao almoço. Quanto comeu cada um?
2. No dia seguinte, os cinco amigos decidiram comprar duas pizas para o almoço e dividi-las
em partes iguais. Que parte de piza comeu cada amigo?
3. O Rodolfo dividiu um chocolate em quatro partes iguais e comeu duas dessas partes.
Que porção do chocolate comeu?
4. Para o lanche na escola havia dois bolos do mesmo tamanho, um de chocolate e outro
de iogurte. O bolo de chocolate foi partilhado igualmente pela Inês, pela Ana e pelo Diogo;
o de iogurte foi partilhado igualmente pela Maria, pelo Tiago, pelo Rui e pela Joana.
a) Com que parte do seu bolo ficou cada uma das crianças?
b) Comeram todas a mesma quantidade de bolo? Explica como pensaste.
30
Algoritmo da multiplicação
Uma loja de artigos de informática fez
uma promoção de impressoras.
No primeiro dia vendeu 12 impressoras.
Quanto recebeu pela venda
das impressoras nesse dia?
A Maria escolheu usar o algoritmo
para calcular, mas calculou de duas
formas:
Discute com os teus colegas as formas de calcular da Maria.
2 3 9 5 18 (18 unidades). Registo
8 unidades e sobra 1 dezena.
2 3 4 5 8 (8 dezenas). Junto 1 dezena que
tinha sobrado e ponho 9.
1 3 9 5 9 (9 dezenas). Ponho 90.
1 3 4 5 4 (4 centenas). Ponho 4 centenas.
Uma forma Outra forma
4 9
3 1 2
9 8
1 4 9 0
5 8 8
4 9
3 1 2
1 8
8 0
9 0
1 4 0 0
5 8 8
1. Efetua as operações seguintes.
a) 36 3 8 c) 128 3 4 e) 93 3 16
b) 45 3 14 d) 62 3 27 f) 273 3 52
CALCULADORA PRODUtOs cURiOsOs
Usa a calculadora para obteres os resultados de:
1 3 999 4 3 999
2 3 999 5 3 999
3 3 999
Observa com atenção os produtos obtidos. O que verificas?
calcula mentalmente:
6 3 999 5 8 3 999 5
7 3 999 5 9 3 999 5
Operações com números naturais
Tarefas que possibilitam uma
exploração dos conteúdos a partir
da análise de situações reais.
261287 001-005.indd 2 30/05/14 17:48

5. 3
Resolução de problemas
Exploração dos conteúdos
a partir de situações da vida
real, com problemas para
aplicares e sistematizares
o que aprendeste.
Páginas de revisão
No fim de cada unidade,
as atividades de revisão
consolidam e reforçam
as tuas aprendizagens.
61
3
6. Uma empresa publicou no final do mês de outubro a informação relativa ao material
produzido e ao material vendido nesse mesmo mês.
Observa a tabela e o gráfico.
Tipo de roupa Quantidade produzida
Calças 120 000
Camisolas 132 500
Camisas 96 540
Bonés 89 450
112
102
96
88,5
60
40
20
0
Bonés
Tipo de roupa
Camisas
Camisolas
Calças
Número
de
peças
(em
milhares)
Vendas no mês de outubro (em milhares)
a) Que quantidade foi vendida de:
calças camisolas
camisas bonés
b) Qual é a diferença entre o número de camisas produzidas e vendidas?
c) Qual foi o tipo de roupa mais vendido? Que quantidade foi vendida?
d) A informação relativa à produção e às vendas foi apresentada de forma diferente.
Descreve a maneira como cada uma foi apresentada.
DESAFIO Um mês De DespOrTO
Todos os dias, o João pratica um só tipo de desporto. Observa a tabela relativa ao tipo
de desporto praticado em cada dia da semana durante um mês.
a) Quantos dias o João:
praticou futebol?
praticou natação à quinta-feira?
praticou atletismo ao sábado?
não praticou natação?
praticou futebol e natação?
b) O mês em que o João fez o registo poderá ter sido o de novembro? porquê?
c) Das seguintes afirmações, copia para o teu caderno apenas as verdadeiras:
Ao fim de semana, o João não praticou natação.
Aos domingos, o João praticou futebol ou atletismo.
2.ª-feira 3.ª-feira 4.ª-feira 5.ª-feira 6.ª-feira sábado Domingo
Natação 2 0 2 3 1 1 0
Futebol 2 3 1 2 2 2 3
Atletismo 0 1 2 0 2 1 1
51
2
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
5. Observa o conjunto de números seguinte.
Indica os elementos do conjunto que:
a) são divisores de 8;
b) são múltiplos de 5;
c) são divisores de 16 e de 24.
6. A Mara e o Diogo são irmãos e estão ambos doentes. Foram ao pediatra e ele
receitou-lhes medicamentos diferentes.
A Mara vai tomar um destes comprimidos
de 8 em 8 horas.
O Diogo vai tomar uma destas cápsulas
de 6 em 6 horas.
Quem termina primeiro o medicamento? Explica como chegaste à tua resposta.
7. Calcula:
a) 126 : 9 b) 761 : 36 c) 477 : 17
1
10 2 8
15
24 12
4 16
3 5
6
Autoavaliação É muito importante refletires
sobre o trabalho realizado em cada unidade e
identificares as tarefas em que sentiste menos
dificuldade e mais dificuldade.
25
1
investiga RegulaRidades no calendáRio
observa o calendário representado e a «cruz» assinalada a rosa.
10 MinUtOs
observa as igualdades.
usa a mesma estratégia de cálculo mental para calculares o resultado de cada uma
das seguintes operações:
a) 34 3 5 b) 16 3 25 c) 8 3 15 d) 24 3 15
3 2
: 2
4 3 25 5 2 3 50 5 1 3 100 5 100
observa agora os números assinalados no calendário. estes números situam-se junto
aos vértices de um quadrado de nove números.
investiga se, em relação
a estes números, é possível
encontrar alguma regularidade.
operações com números naturais
Dom. Seg. Ter. Qua. Qui. Sex. Sáb.
1 2 3 4 5 6.
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
Dom. Seg. Ter. Qua. Qui. Sex. Sáb.
1 2 3 4 5 6.
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
adiciona todos os números do interior
da «cruz». existirá alguma relação entre
a soma obtida e o número que está
no centro da «cruz»?
copia o calendário para o teu caderno
e pinta outras «cruzes». investiga,
em grupo, se há alguma regularidade
entre a soma de todos os números
de cada «cruz» e o número central.
126
4. No recreio, mede um comprimento de 10 metros
com um metro articulado. Marca as duas
extremidades com giz. Estica e corta um fio
que ligue os dois pontos marcados.
a) Qual é o comprimento, em decâmetros, do fio?
b) Faz uma estimativa do comprimento do recreio
da tua escola. Efetua a medição.
5. Em cada situação indica uma unidade de medida que usarias para efetuar a medição.
Estima as medidas e, de seguida, mede usando material adequado
(régua, metro articulado ou fio de 1 dam).
a) Copia a tabela para o teu caderno e completa-a.
Unidades de medida de comprimento
b) Compara as estimativas com as medidas obtidas.
6. Indica duas situações em que recorrerias ao quilómetro para efetuar medições.
Tal como o decâmetro, o hectómetro (hm) e o quilómetro (km) são unidades
de medida de comprimento maiores do que o metro.
1 hm 5 100 m 1 km 5 1000 m
O metro é a centésima parte do hectómetro. 1 m 5
1
100
hm 5 0,01 hm
O metro é a milésima parte do quilómetro. 1 m 5
1
1000
km 5 0,001 km
Não te esqueças!
Unidade
de medida
Estimativa Valor real
Espessura da moeda
de 1 euro
Altura de uma porta
Largura do teu livro
de Matemática
Comprimento de um
muro da tua escola
Figuras no plano e sólidos geométricos
Não te
esqueças!
Conceito
fundamental.
Investiga
Área na qual vais
poder investigar
e descobrir algumas
propriedades
matemáticas.
10 minutos
Atividade
de aplicação
de conteúdos
a desenvolver
num curto espaço
de tempo.
DESAFIO Área na
qual é proposto
um problema mais
desafiante,
envolvendo
processos com
um grau de
complexidade
superior. 139
8
Comprimento, massa, capacidade, área e volume
1. Considera os sólidos de A a H.
Visualização espacial
Observa o sólido e as respetivas vistas.
a) Copia a tabela seguinte para o teu caderno e completa-a com a letra do sólido
associado a cada combinação da vista de cima com a de frente. Vê o exemplo.
b) Determina o volume e a área dos sólidos C, D e H usando como unidades o
e o respectivamente. Identifica sólidos equivalentes.
Vista de cima
Vista
de frente
Sólido G
Vista de frente Vista de lado Vista de cima
Vista de cima
Vista de lado
Vista de frente
DESAFIO O CubO merGulHADO
O Alexandre mergulhou um cubo constituído por pequenos cubinhos ( ) numa lata
de tinta vermelha. Deixou secar e de seguida desmontou-o.
Observa as imagens.
Diz quantos cubos pequenos ( ) ficaram com:
— três faces pintadas; duas faces pintadas;
uma face pintada; nenhuma face pintada.
A H
b C D e F G
97
5
Números racionais não negativos
Ordenar números racionais
Jogo Jogo dos racioNais
Preparem 30 cartões e, com a ajuda do professor, escrevam um número racional
em cada cartão (frações, números inteiros e números decimais).
organizem equipas de cinco elementos (são necessárias pelo menos duas equipas)
e escolham um árbitro.
Regras do jogo:
cada equipa tira 5 cartões sem ver os números.
Quando o árbitro der sinal, cada equipa distribui um cartão por cada elemento
e depois devem alinhar-se de acordo com a ordem dos cartões.
ganha a equipa que estiver mais rapidamente alinhada.
Também podes jogar o jogo sentado à mesa com o teu parceiro, sendo que, assim,
cada um de vocês tem de ordenar os seus cinco cartões.
durante o Jogo dos racionais, o rafael sentiu algumas dificuldades. observa a sua
conversa com a Mara.
1. E tu, já percebeste? ordena cada um dos seguintes conjuntos de cartões.
a) b)
o meu cartão tem
o número 5…
E qual é maior?
o meu ou o teu?
Lê-se cinco unidades e três
décimas. o meu lê-se três
unidades e quarenta e cinco
centésimas.
começas por comparar a parte
inteira. o teu número é maior
porque tem mais unidades.
Exatamente: o Luís tem o
cartão com o número 5,7. Tem
as mesmas unidades, por isso
tens de comparar as décimas.
Já percebi. como
o número do Luís
tem sete décimas, ele
tem um número maior
do que o meu.
5,15 3,4 4,5
0,7 3,2
3,25 4,05 3,28
4,5 3,7
Jogo Atividade
a desenvolver
em grupo, em
que se trabalha
a Matemática
de forma
divertida.
261287 001-005.indd 3 30/05/14 17:48

6. 4
ÍNDICE
Página
Meses
REVISÃO
SETEMBRO/OUTUBRO
1
UNIDADE
Números naturais
Operações com números
naturais
Números naturais
Operações com números
naturais
Dezenas e centenas de milhar
Os milhões
Milhares de milhão e bilião
Adição e subtração
Múltiplos de um número natural
Tabuada do 11
Tabuada do 12
Multiplicação
Introdução ao algoritmo da multiplicação
Resolução de problemas
Algoritmo da multiplicação
Resolução de problemas
REVISÃO
NOVEMBRO
2
UNIDADE
REVISÃO
32
35
38
40
42
45
46
48
13
15
16
17
20
22
23
26
27
28
30
31
52
Números racionais não
negativos
Frações em vários contextos
Frações e percentagens
Frações e medida de áreas
Frações
Adicionar e subtrair frações
Multiplicar e dividir frações
Números decimais
Fração e representação decimal
Ordenar números racionais
A milésima
Estimar e calcular com números decimais
93
97
98
99
100
102
104
105
107
108
110
112
FEVEREIRO
5
UNIDADE
Conteúdos
Tópicos
Avaliação de diagnóstico 6
Operações com números
naturais
Divisão
Multiplicação e divisão
Calculando em cadeia
Divisores de um número natural
Divisão inteira
Resolução de problemas
Algoritmo da divisão
UM C D U
0
DM
7 0 0 0
Representação
e interpretação de dados
e situações aleatórias
Figuras no plano
e sólidos geométricos
Pictogramas
Gráfico de barras e gráfico de pontos
Diagrama de caule-e-folhas
Gráfico circular
Diagrama de Carroll
Frequências relativas
Resolução de problemas
Situações aleatórias
Sólidos geométricos
Prismas retos
Planificações
Círculo e circunferência
Raio e diâmetro
Noção de ângulo
Amplitude de um ângulo
Identificar e comparar ângulos
Retas paralelas e retas concorrentes
Simetrias de reflexão
Frisos
REVISÃO
55
56
58
59
60
61
62
65
71
72
73
74
75
77
78
79
84
86
88
90
68
REVISÃO
DEZEMBRO
3
UNIDADE
JANEIRO
4
UNIDADE
Tipo de alimentação
Saudável
Não saudável
261287 001-005.indd 4 30/05/14 17:48

7. 5
Página
Meses
Números racionais não
negativos
Regularidades
Calcular com números decimais
Multiplicar por 0,1, por 0,01 e por 0,001
Multiplicar e estimar com números decimais
Algoritmo da multiplicação com números decimais
Divisão com números decimais
Dividir por 0,1, por 0,01 e por 0,001
Algoritmo da divisão com números decimais
Resolução de problemas
Quociente da divisão inteira, quociente e dízima
Algoritmo da divisão com números decimais
para o cálculo aproximado de quocientes
Sequências e regularidades
Regularidades numéricas
Contagens visuais. Traduzir contagens visuais por
expressões numéricas
Padrões de repetição
Padrões de crescimento
REVISÃO
REVISÃO
MARÇO
JUNHO
Abril
MAIO
6
UNIDADE
9
UNIDADE
7
UNIDADE
8
UNIDADE
Comprimento,
massa, capacidade,
área e volume
Figuras no plano
e sólidos geométricos
Comprimento,
massa, capacidade,
área e volume
Volume
Visualização espacial
Comparação e estimativa de volumes
Unidades de medida de volume
Volume de um paralelepípedo
Volume
Unidades de medida de capacidade
Massa
Relação entre volume/capacidade
e entre massa/capacidade
Resolução de problemas
REVISÃO
REVISÃO
115
117
118
120
122
123
124
126
128
129
167
168
169
170
172
130
174
151
153
154
155
156
158
159
160
161
162
148
164
Conteúdos
Tópicos
Números e operações Medida
Geometria Organização e tratamento de dados
Autoavaliação 176
Comprimento
Unidades de medida de comprimento
Resolução de problemas
Área
Unidades de medida de área
Medidas agrárias
Área de um retângulo
Pavimentações
Visualização
136
137
139
140
143
145
146
133
134
261287 001-005.indd 5 30/05/14 17:48

8. 6
6
Avaliação de diagnóstico
Responde às questões no teu caderno diário.
1. Determina aproximadamente os números correspondentes às letras A, B, C, D, E e F.
Ficha n.o
1
A
1200
B C D E F
400 500 600 700 800 900 1000 1100
2. Para cada uma das seguintes sequências determina uma possível regra de formação e,
de acordo com essa regra, escreve no teu caderno os cinco números seguintes.
a) 232 242 252
b) 405 425 445
c) 25 75 125
d) 927 827 727
3. Completa as tabelas.
4 1 5 10
2 1 5 10
7 1 5 10
12 1 5 20
16 1 5 20
11 1 5 20
30 1 5 100
25 1 5 100
64 1 5 100
400 1 5 1000
750 1 5 1000
825 1 5 1000
4. Observa a sequência de retângulos que se segue e determina uma possível
regra de formação.
Fig. 1 Fig. 2 Fig. 3 Fig. 4
a) De acordo com essa regra de formação, desenha o quinto retângulo desta sequência.
b) De acordo com essa regra de formação, qual será a área, em quadrículas, do sexto
retângulo desta sequência? Desenha-o no teu caderno.
c) Completa a tabela, de acordo com essa regra de formação.
d) Qual é a área da trigésima figura? Explica o teu raciocínio.
Número da figura 1 2 3 4 5 6 7 8 10 20
Área (em quadrículas) 2 4 6 8
Perímetro (lado da quadrícula) 6 8 10 12
261287 006-011.indd 6 30/05/14 17:47

9. 7
7
Avaliação de diagnóstico
Responde às questões no teu caderno diário.
Ficha n.o
2
1. Desenha no teu caderno uma planta do teu quarto. Compara a tua planta com as dos teus
colegas.
2. Classifica cada uma das figuras geométricas quanto ao número de lados.
A B C D E F G H
3. Observa os seguintes sólidos geométricos.
a) Escreve no teu caderno o nome de cada um dos sólidos anteriores.
b) Destes sólidos, indica:
um que tenha uma face triangular.
um que tenha uma face quadrada.
um que tenha uma face circular.
c) Dos sólidos representados, indica:
um que tenha 8 vértices e 12 arestas.
um que tenha 6 vértices e 9 arestas.
um que tenha 5 vértices e 8 arestas.
4. Calcula o resultado de cada uma das seguintes operações usando uma estratégia
de cálculo à tua escolha.
a) 345 1 230 b) 565 2 230 c) 231 1 149 d) 900 2 324
I
K
L
J
A
B
C
G
H
D
E
F
A B E
C D F G H
261287 006-011.indd 7 30/05/14 17:47

10. 8
8
Avaliação de diagnóstico
Responde às questões no teu caderno diário.
Ficha n.o
3
1. A Joana foi à frutaria.
a)
Se comprasse 10 quilos de laranjas,
quanto pagaria? E se comprasse
10 quilos de maçãs?
b) Se comprasse 2 quilos de laranjas
e 2 quilos de maçãs, quanto pagaria?
c) A Joana acabou por comprar só uvas
e figos. Pagou com uma nota de 5
euros e recebeu de troco uma moeda
de 1 euro, uma moeda de 50 cêntimos
e uma de 5 cêntimos. Quanto custou
a fruta?
a)
b)
c)
d)
e)
f)
3. Qual é a fração que corresponde à parte pintada de cada figura?
2.
O João, o Miguel e o Tomás foram almoçar juntos a casa do Tomás.
a) Dividiram uma piza igualmente pelos três.
Que parte de piza comeu cada um?
b) Depois do almoço, o irmão do Tomás juntou-se
aos amigos para brincarem com berlindes.
Divide igualmente os berlindes pelos quatro
amigos. Com quantos berlindes ficará cada um?
261287 006-011.indd 8 30/05/14 17:47

11. 9
9
Avaliação de diagnóstico
Responde às questões no teu caderno diário.
a)
Faz uma estimativa, em centímetros, do perímetro de cada figura e regista
os valores no teu caderno.
b) Utiliza uma régua para medires o perímetro de cada figura e compara o resultado
com a estimativa que fizeste na alínea anterior.
c) Desenha no teu caderno uma figura cujo perímetro seja igual ao da figura C.
2. O Sr. Aníbal aproveitou a feira anual
para vender alguns dos seus animais.
a)
Vendeu 230 das suas 456 galinhas.
Com quantas galinhas ficou?
b)
Vendeu metade das suas 46 vacas.
Quantas vacas vendeu?
c)
Vendeu 65 porcos e ficou com 54.
Quantos porcos tinha inicialmente?
d)
Vendeu 135 coelhos a 3 € cada.
Quanto rendeu a venda
dos coelhos?
3. Completa o esquema.
Ficha n.o
4
1. Observa as figuras seguintes.
5
3 100
: 3
: 2
: 100
3 10
3 1000
3 2
3 3
: 1000
: 10
A B C
261287 006-011.indd 9 30/05/14 17:47

12. 10
10
Avaliação de diagnóstico
Responde às questões no teu caderno diário.
1. Descobre os números e regista-os na tabela.
Ficha n.o
5
2. A Beatriz tem duas saias, uma azul e outra vermelha, e três camisolas, uma amarela, uma
branca e outra vermelha, para vestir à sua boneca. De quantas formas diferentes pode
vestir a boneca?
Número Estou entre Sou múltiplo de Sou múltiplo de Sou o número
A 10 e 20 3 5
B 20 e 30 6 8
C 70 e 90 10 4
D 40 e 50 3 7
E 90 e 110 4 5
3. Desenha quatro relógios iguais a este e marca em cada
um a hora a que:
te levantas de manhã;
chegas à escola;
sais da escola;
vais dormir.
4. A Matilde está a juntar moedas para ir comprar gomas.
Tem consigo 2,45 €.
a) A mãe deu-lhe mais 1,35 €. Com quanto ficou?
b) Comprou 20 gomas a 10 cêntimos cada
e 15 gomas a 5 cêntimos cada.
Quanto dinheiro lhe sobrou?
261287 006-011.indd 10 30/05/14 17:47

13. 11
11
Avaliação de diagnóstico
Responde às questões no teu caderno diário.
1. Observa o gráfico seguinte, onde estão registadas as espécies dos animais
de estimação dos alunos da turma do Miguel.
Ficha n.o
6
0
Cão Coelho
Espécies dos animais de estimação
Gato Hamster
Número
de
animais
15
10
5
Espécies dos animais de estimação dos alunos da turma do Miguel
a) Quantos gatos têm ao todo os meninos desta turma?
b) Pensando apenas nestes animais, qual é a espécie mais frequente?
c) Se todos os meninos trouxessem os seus animais para a escola, quantos animais
seriam ao todo?
2.
O Rodrigo e a Lara colocaram dentro de um saco preto
quatro bolas vermelhas, uma bola amarela e uma bola azul.
a) Se tirarem uma bola do saco, quais são as possíveis
cores que a bola pode ter?
b) O Rodrigo vai tirar uma bola. Qual é a cor mais provável?
Porquê?
c) O Rodrigo tirou uma bola amarela e agora a Lara vai retirar uma bola.
Quais são as cores possíveis para essa próxima bola?
3. A professora Isabel está a preparar 3 mesas para o lanche especial do primeiro dia
de aulas. Ela tem consigo 24 pacotes de sumo, 9 bolos de iogurte e 7 bolos
de chocolate. Tenta fazer um esquema no teu caderno de modo a dividires igualmente
os sumos e os bolos de cada tipo pelas três mesas. Foi possível colocar as mesmas
quantidades em cada mesa? Explica o teu raciocínio.
261287 006-011.indd 11 30/05/14 17:47

14. 12
1
UNIDADE
A nova turma do Miguel está a fazer uma pesquisa sobre
dinossauros na biblioteca. Conheces algumas características
destes animais?
Miguel, diz aqui que
alguns dinossauros
herbívoros podiam atingir
30 m de comprimento
e 70 000 kg de peso.
Sim, e diz também que
os dinossauros terão
desaparecido há cerca
de 65 milhões de anos.
Eram enormes!
Milhões de anos?
261287 012-033.indd 12 30/05/14 17:49

15. 13
15 000 25 000
22 500 32 500
20 000 18 000
15 000 30 000
9000 11 000
1.
Na reta numérica anterior, posiciona os números seguintes usando as letras respetivas.
a) A — 15 000 C — 45 000 E — 62 500
B — 92 000 D — 79 000 F — 21 500
b) Ordena os números anteriores por ordem crescente.
c) Escreve por extenso o número representado pela letra E.
2.
Para cada uma das seguintes sequências determina uma possível regra de formação e,
de acordo com essa regra, escreve os quatro números seguintes.
Dezenas e centenas de milhar
Repara no número que representa o peso daquele dinossauro em quilogramas.
Observa as representações seguintes.
Classe dos milhares Classe das unidades
C D U C D U
7 0 0 0 0
0 10 000 20 000 30 000 40 000 50 000 60 000 70 000 80 000 90 000 100 000
UM C D U
0
DM
7 0 0 0
Números naturais
261287 012-033.indd 13 30/05/14 17:49

16. 10 MINUTOS
Os cientistas estimaram
a velocidade média que o famoso
dinossauro Tyrannosaurus rex
podia atingir. A partir das pistas
seguintes, descobre a sua
velocidade (em km/h).
É um número de dois algarismos.
Não é ímpar.
O algarismo das unidades
é o dobro do das dezenas.
A soma dos algarismos é 12.
14
3.
Observa a seguinte reta numérica.
70 000 80 000 90 000 100 000 110 000 120 000 130 000 140 000 150 000
A B C D E F
CM DM UM C D U Decomposição Escrita por extenso
1 5 4 2 0 0
100 000 + 50 000 + 4000 +
200
Cento e cinquenta e quatro mil
e duzentos
5 1 0 3 0 5
20 000 + 700
Noventa e três mil e trezentos
2500 5250 13 000 50 000 125 000 100
1000
10 000
100 000
1
Números naturais
5. Calcula.
Faz corresponder a cada um dos números indicados em baixo uma das posições
assinaladas por uma letra na reta numérica.
105 000 — 86 000 — 135 000 —
119 000 — 99 000 — 143 000 —
4.
Completa a tabela seguinte, de acordo com o exemplo.
Foto: LTShears
Dezenas e centenas de milhar
261287 012-033.indd 14 30/05/14 17:49

17. 15
1
Os milhões
Classe dos milhões Classe dos milhares Classe das unidades
C D U C D U C D U
6 5 0 0 0 0 0 0
Números naturais
a)
Usando algarismos, escreve os valores das estimativas do início
do período em que cada uma destas espécies de dinossauros habitou a Terra.
b) Identifica aquela que viveu há mais tempo e aquela que viveu há menos tempo.
1.
Observa a tabela seguinte, com informações sobre alguns dinossauros famosos.
Investiga números grandes
Lê o diálogo entre o Guilherme e a Joana.
Nós temos 9 anos.
Já vivemos mais
de 1 milhão de horas!
Não acredito! Era preciso
viver mais de 100 anos para
viver 1 milhão de horas.
Investiga e verifica quem tem razão: se o Guilherme ou se a Joana.
Estimativa do início do período em que habitaram a Terra
Tyrannosaurus rex
Há 67 milhões
de anos.
Oviraptor
Há 80 milhões
de anos.
Brachiosaurus
Há 150 milhões
de anos.
Triceratops
Há 68 milhões
de anos.
A Filipa referiu um número muito grande, quando disse que os dinossauros terão
desaparecido há 65 milhões de anos. Para representar esse número, precisamos de uma
outra classe: a classe dos milhões.
Utilizando regras análogas às utilizadas para a contagem até ao milhão, poderás prosseguir
a contagem indefinidamente.
Marcin Floryan Marcin Floryan
Marcin Floryan
261287 012-033.indd 15 30/05/14 17:49

18. 16 Operações com números naturais
Milhares de milhão e bilião
O nosso planeta ter-se-á formado há cerca de 4 500 000 000 de anos. Em Portugal dizemos
que a Terra tem 4,5 mil milhões de anos. Contudo, no Brasil diz-se que a Terra tem 4,5
biliões de anos. Porque será que isto acontece?
Vejamos a seguinte tabela:
1.
Completa a tabela, de acordo com o exemplo.
Portugal (e outros
países da Europa)
Brasil (e EUA)
1000 mil mil
1 000 000 milhão milhão
1 000 000 000 mil milhões bilião/bilhão (billion)
1 000 000 000 000 bilião trilião
314 012 300 000 1 10 000 1 4000 1 10 1 2
1 701 430
9 950 900
52 075 100
5 340 000 000
Em alguns países há diferenças na leitura dos números a partir da classe dos milhões.
2.
Completa com ., , ou 5.
a) Cento e quarenta e um mil e cem 1 410 100
b) Duzentos e cinquenta mil, cento e doze 250 112
c) Doze milhões e trezentos e vinte mil 12 032 000
d) Dois mil quatrocentos e cinco milhões 2 450 000 000
3.
Indica a ordem de cada um dos algarismos coloridos nos números seguintes.
a) 351 420 b) 2 345 000 c) 150 300 000
4.
Escreve, por extenso, a leitura dos seguintes números.
a) 21 007
b) 17 450 073
c) 2 000 000 000
261287 012-033.indd 16 30/05/14 17:49

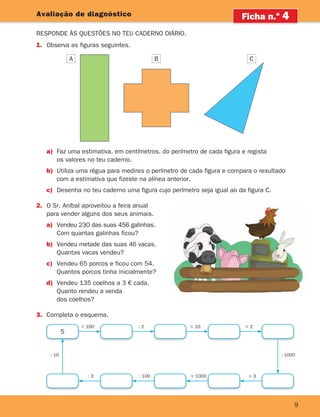
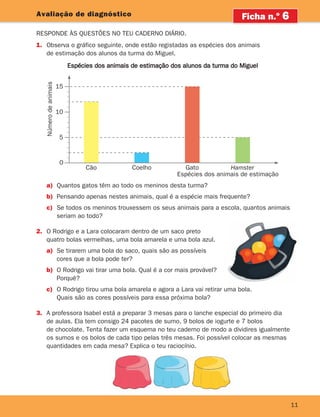
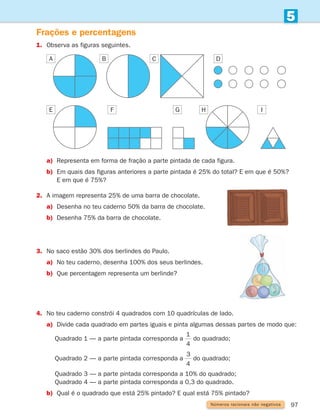
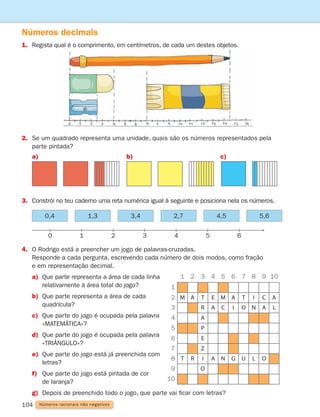
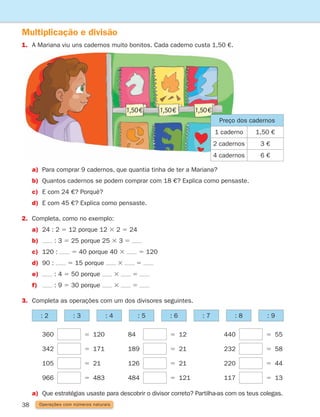
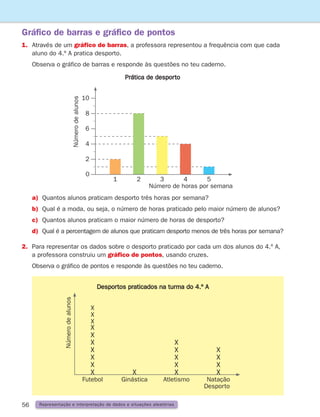
19. 17
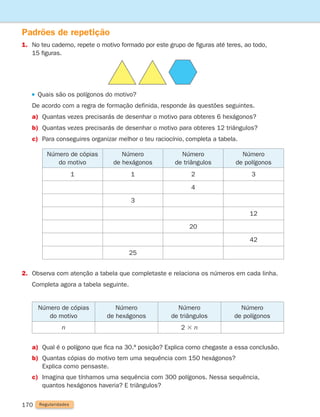
1
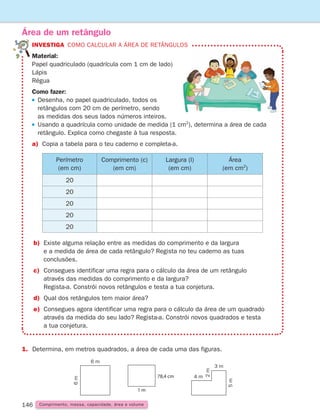
Adição e subtração
1. Descobre quais são os números escondidos e escreve-os nos quadrados.
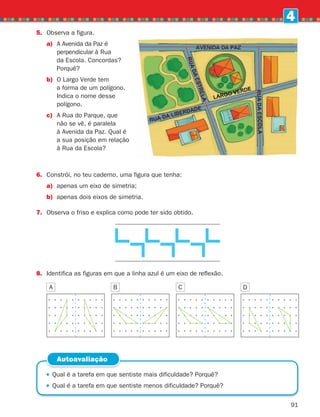
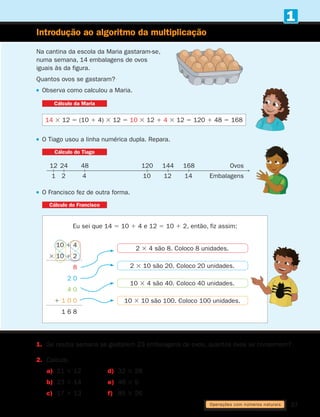
a) 80 1 5 120 c) ] 55 5 145 e) 1 0,5 5 3,5
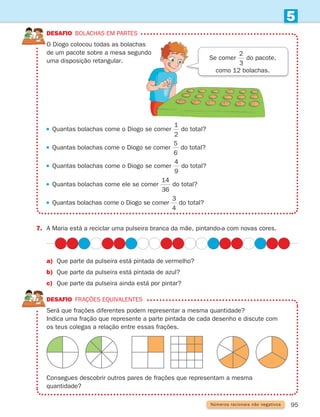
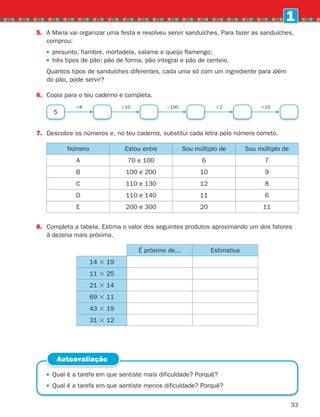
b) 1 90 5 150 d) 195 ] 5 150 f) 12 ] 5 9,5
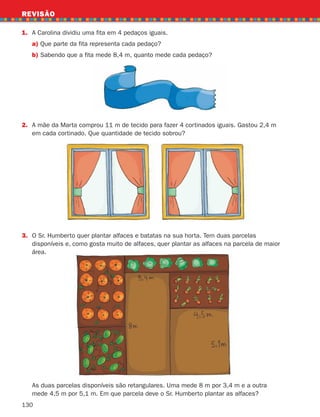
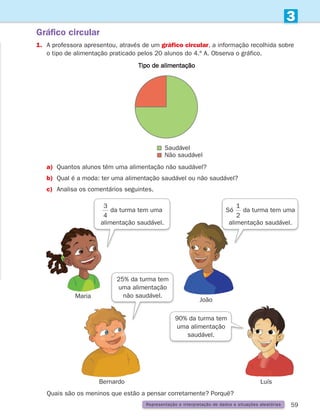
2.
A Joana andou pela primeira vez de autocarro este verão. Sentou-se ao fundo para ver
quem entrava e quem saía.
a)
Entraram inicialmente 47 passageiros. Na primeira paragem saíram 17 e entraram
12. Na segunda paragem saíram 9 e entraram 11. Quantos passageiros chegaram
à terceira e última paragem?
b)
Se o conta-quilómetros do autocarro marcava 12 781 quilómetros no início do percurso
e 12 849 quilómetros no final, qual foi a distância percorrida pelo autocarro?
c)
Quanto marcaria o conta-quilómetros se o autocarro andasse mais 1 quilómetro?
E mais 10 quilómetros? E mais 200 quilómetros?
3.
Copia para o teu caderno e coloca no o algarismo correto.
a) 3 7
1 2 4
4 9
b)
2 7
1 3
6 9
c) 9 6
1 6
2 1 1
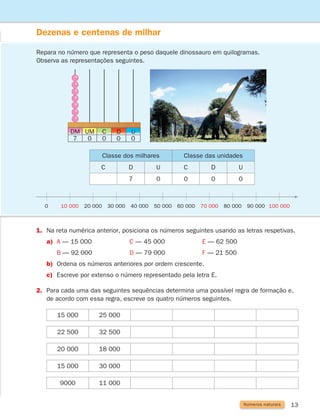
Operações com números naturais
261287 012-033.indd 17 30/05/14 17:49

20. CALCULADORA Vamos investigar diferenças
tarefa 1
Escolhe três algarismos diferentes.
Podes começar, por exemplo, por estes:
18
Maior número: 642
642 2 246 5 396
Menor número: 246
Escreve o maior número e o menor número, que podem ser formados por estes
três algarismos.
Calcula, com a calculadora, a diferença entre o maior número e o menor número
e regista-a.
Com os algarismos obtidos, volta a formar o maior número e o menor número
e calcula a diferença.
Repete o processo sucessivamente. O que verificas?
Escolhe agora outros três algarismos diferentes e repete o procedimento.
Que regularidades parecem existir?
Experimenta em mais conjuntos de três algarismos.
tarefa 2
Experimenta agora utilizar quatro algarismos diferentes.
Que regularidades consegues encontrar?
Experimenta em mais conjuntos de quatro algarismos.
Partilha as tuas descobertas: elabora um cartaz em que expliques o que
descobriste e apresenta-o à turma numa «conferência matemática».
2 6
4
Adição e subtração
Operações com números naturais
10 MINUTOS
Calcula mentalmente o resultado de cada uma das operações seguintes.
390 1 110 720 1 180 225 1 175
420 1 220 950 1 500 1500 1 300
261287 012-033.indd 18 30/05/14 17:49

21. 19
a)
Faz uma estimativa dos resultados de cada uma das operações anteriores,
arredondando cada número à centena mais próxima.
b)
Calcula o valor exato do resultado de cada uma das
operações anteriores.
5.
O pai do Diogo nasceu a 25 de outubro de 1977.
Qual é a sua idade?
a)
O Diogo nasceu a 15 de janeiro e tem 9 anos.
Que idade tinha o seu pai quando ele nasceu?
6.
Observa a tabela com os dados de uma visita de estudo dos alunos de uma escola
ao Oceanário de Lisboa.
1
4.
Observa as seguintes operações.
234 1 89 339 2 97 684 1 321 592 2 289
Hora
de saída
Hora
de chegada
Número
de crianças
Número
de adultos
Número
de lugares
de cada
autocarro
Preço
do aluguer
de cada
autocarro
8h 15 17h 30 163 14 55 290 €
22
Ana
Anotaram a data da maratona. Seco de raiva, coloco no colo caviar e doces.
101
osso
555
saias
12 521 370 000 073
DESAFIO Palíndromos e capicuas
Observa com atenção os números, palavras e frases seguintes.
O que têm em comum?
Escreve no teu caderno outros números que sejam capicuas e descobre uma
palavra que seja um palíndromo.
Investiga, com recurso à Internet, um pouco mais sobre palíndromos e capicuas
e escreve um pequeno relatório sobre este tema, em que exponhas as tuas
principais descobertas.
a)
Formula dois problemas diferentes usando esta informação.
Operações com números naturais
261287 012-033.indd 19 30/05/14 17:49

22. 20 Números naturais
Múltiplos de um número natural
1.
Observa a tabela da centena.
a)
O que podes afirmar sobre a disposição
dos números da tabela?
Discute as tuas descobertas com os teus colegas
de grupo e descreve no teu caderno
as regularidades que encontraram.
b)
Usa uma tabela igual a esta e procede
da seguinte forma:
Pinta da mesma cor todos os números que
são múltiplos de 4, ou seja, começa no 4
e vai pintando todos os números de 4 em 4.
Pinta de outra cor todos os números que são múltiplos de 8, ou seja,
começa no 8 e vai pintando todos os números de 8 em 8.
Há números que ficaram pintados com duas cores. Quais são?
Explica por que razão terá isto acontecido.
O que descobriste sobre os múltiplos de 4 e de 8?
2.
Usa a tabela da centena para investigares as relações entre os múltiplos de 3
e os múltiplos de 6. Podes usar um procedimento semelhante ao que seguiste
na tarefa anterior.
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
Vamos olhar para
os números da tabela
da centena.
Que regularidades
consegues descobrir?
261287 012-033.indd 20 30/05/14 17:49

23. 21
Números naturais
1
3. Observa as retas numéricas.
a)
Completa.
30 42 18 9 20 14 45 22 44
Regista aqueles que são múltiplos de:
a) 4: d) 9:
b) 5: e) 11:
c) 6: f) 15:
5. Descobre um intruso nos conjuntos de números seguintes. Justifica a tua resposta.
A B
15
45
60
105
55
75
0
30
14
0
42
70
84
21
35
29
b)
Obtiveste os múltiplos de 2 e de 3 inferiores a 20. Indica os números que são
simultaneamente múltiplos de 2 e de 3.
4.
Observa os números.
10 MINUTOS
Usando quatro vezes o algarismo 6 e uma ou mais das operações que conheces,
descobre uma forma de obter o número 12.
8x2
7x2
6x2
5x2
4x2
3x2
2x2
4
1x2
2
+2
9x2
1x3
3
2x3
261287 012-033.indd 21 30/05/14 17:49

24. Jogo Bingo das tabuadas
Vais precisar de um cartão de jogo, como o da figura.
O professor irá ler, lentamente e em voz alta, algumas
operações:
5 3 9, 7 3 3, 11 3 4, 8 3 8, …
Se o resultado de alguma dessas operações se encontrar no
teu cartão, deves assinalar o número em causa. Quem primeiro
conseguir assinalar todos os números contidos no cartão deve dizer:
«Bingo», e é vencedor.
22
1.
Para fazer a tabuada do 11, o Diogo utilizou os resultados das tabuadas do 1 e do 10,
que já conhecia. Observa o seu registo.
Tabuada do 11
Operações com números naturais
28 81 56
27 48 30
63 72 12
a)
Completa a tabela.
b)
Observa com atenção os produtos da tabuada do 11.
Que regularidades encontras?
2.
Regista no teu caderno todos os múltiplos de 11, menores do que 180.
3. Calcula os resultados das operações seguintes.
a) 3 3 11 c) 6 3 11 e) 10 3 11 g) 24 3 11
b) 5 3 11 d) 9 3 11 f) 12 3 11 h) 100 3 11
Para descobrir
3 3 11,
decomponho o 11 em 10 1 1
e faço
3 3 10 1 3 3 1 5 30 1 3 5 33
3 10 1 11
1 10 1 11
2 20 2 22
3 30 3 33
4
5
6
7
8
9
10
11
12
261287 012-033.indd 22 30/05/14 17:49

25. 23
1
1.
No casamento do tio da Francisca, as mesas dos convidados eram circulares.
Em cada mesa sentaram-se 12 convidados, como ilustra a figura.
a) Quantas pessoas se sentam em redor de 2 mesas?
b) E em redor de 4 mesas?
c) E em redor de 3 mesas?
d) E em redor de 10 mesas?
e) E em redor de 5 mesas?
f) Determina ainda quantas pessoas se sentam à volta de 6, 7, 8, 9, 11 e 12 mesas.
Partilha com os colegas as estratégias que usaste.
2.
Os resultados que obtiveste no exercício anterior são os produtos da tabuada do 12.
Escreve-os.
3. Completa, de modo a obteres uma afirmação verdadeira.
a) 3 9 é um número compreendido entre 40 e 50.
b) 3 6 é um número compreendido entre 45 e 52.
c) 11 3 é um número compreendido entre 32 e 40.
d) 3 12 é um número compreendido entre 90 e 100.
e) 3 12 é um número compreendido entre 115 e 130.
Partilha com os teus colegas as estratégias que usaste.
Operações com números naturais
Tabuada do 12
261287 012-033.indd 23 30/05/14 17:49

26. 10 MINUTOS
Para cada uma das seguintes sequências, determina uma possível regra de formação
e, de acordo com essa regra, escreve os cinco números seguintes.
120, 132, 144, , , , ,
348, 336, 324, , , , ,
374, 398, 422, , , , ,
24
Completa a tabela.
O que podes afirmar sobre os números da tabela? Discute as tuas descobertas
com os teus colegas de grupo e descreve no teu caderno as regularidades que
descobriram.
Usa uma tabela igual a esta e assinala com lápis de cor os múltiplos de 6.
Que regularidades observas?
Investiga o que acontecerá com outros múltiplos.
investiga tabela 12 3 12
Observa a tabela de números seguinte.
1 2 3 4 5 6 7 8 9 10 11 12
2 4 6 8 10 12 14 16 18 20 22 24
3 6 9 12 15 18 21 24 27 30 33 36
4 8 12 16 20 24 28 32 36 48
5 10 20
6 18 24 30 48 66
7 21 42 49 63 84
8 32 48 64 96
9 72
10
11
12
Operações com números naturais
261287 012-033.indd 24 30/05/14 17:49

27. 25
1
investiga Regularidades no calendário
Observa o calendário representado e a «cruz» assinalada a rosa.
10 MINUTOS
Observa as igualdades.
Usa a mesma estratégia de cálculo mental para calculares o resultado de cada uma
das operações seguintes.
a) 34 3 5 b) 16 3 25 c) 8 3 15 d) 24 3 15
3 2
: 2
4 3 25 5 2 3 50 5 1 3 100 5 100
Observa agora os números assinalados no calendário. Estes números situam-se nos
vértices de um quadrado de nove números.
Investiga se, em relação
a estes números, é possível
encontrar alguma regularidade.
Operações com números naturais
Dom. Seg. Ter. Qua. Qui. Sex. Sáb.
1 2 3 4 5 6.
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
Dom. Seg. Ter. Qua. Qui. Sex. Sáb.
1 2 3 4 5 6.
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
Adiciona todos os números do interior
da «cruz». Existirá alguma relação entre
a soma obtida e o número que está
no centro da «cruz»?
Copia o calendário para o teu caderno
e pinta outras «cruzes». Investiga,
em grupo, se há alguma regularidade
entre a soma de todos os números
de cada «cruz» e o número central.
261287 012-033.indd 25 30/05/14 17:49

28. 26
Multiplicação
A mãe da Beatriz vai comprar 5 molduras ovais para
pendurar na parede da sala. Quer saber quanto gastará,
aproximadamente.
Pensou assim: «5 3 19 é próximo de 5 3 20, então, vou
gastar pouco menos de 100 euros.»
1.
Completa a tabela. Estima o valor de cada um dos seguintes produtos aproximando
um dos fatores à dezena mais próxima, tal como no exemplo.
Calcula os resultados das operações usando uma destas estratégias.
a) 5 3 18 b) 6 3 13 c) 12 3 22 d) 19 3 4
É próximo de... Estimativa
5 3 19 5 3 20 100
7 3 19 7 3
29 3 10 3 10
18 3 40
78 3 20
61 3 19
2. Observa as diferentes estratégias utilizadas para calcular rapidamente 7 3 28.
7 3 28
Operações com números naturais
Pensei em sete vezes
25, que dá 175.
Depois precisei de sete
vezes 3, ou seja 21.
Por isso, a resposta
é 175 1 21 5 196.
Calculei 7 3 30,
que é 210.
Depois retirei
sete vezes 2, ou seja,
14, o que dá 196.
7 3 20 é 140
e 7 3 8 é 56
140 1 56 5 196
261287 012-033.indd 26 30/05/14 17:49

29. 27
1
Introdução ao algoritmo da multiplicação
Na cantina da escola da Maria gastaram-se,
numa semana, 14 embalagens de ovos
iguais às da figura.
Quantos ovos se gastaram?
Observa como calculou a Maria.
O Tiago usou a linha numérica dupla. Repara.
O Francisco fez de outra forma.
14 3 12 5 (10 1 4) 3 12 5 10 3 12 1 4 3 12 5 120 1 48 5 168
Cálculo da Maria
Cálculo da Maria
Cálculo do Tiago
Cálculo do Tiago
Cálculo do Francisco
Cálculo do Francisco
Eu sei que 14 5 10 1 4 e 12 5 10 1 2, então, fiz assim:
2 3 4 são 8. Coloco 8 unidades.
2 3 10 são 20. Coloco 20 unidades.
10 3 4 são 40. Coloco 40 unidades.
10 3 10 são 100. Coloco 100 unidades.
10 1 4
3 10 1 2
8
2 0
4 0
1 1 0 0
1 6 8
1. Se noutra semana se gastarem 23 embalagens de ovos, quantos ovos se consomem?
2. Calcula.
a) 21 3 12 d) 32 3 28
b) 23 3 14 e) 46 3 5
c) 17 3 13 f) 85 3 26
1
12
2
24
4
48
10
120
12
144
14
168
Embalagens
Ovos
Operações com números naturais
261287 012-033.indd 27 30/05/14 17:49

30. RESOLUÇÃO DE PROBLEMAS
DESAFIO As compras do Francisco
O Francisco foi ao supermercado com os pais comprar
iogurtes. Escolheram alguns iogurtes em embalagens
de 4 e outros em embalagens de 6. Compraram
7 embalagens, num total de 32 iogurtes.
Quantas embalagens de cada tipo compraram?
28
1.
O Sr. Manuel vende várias espécies de plantas
para transplantar. Um dia, levou para o mercado
15 tabuleiros de pepineiros iguais aos
da figura representada ao lado. Quantas
plantas levou?
2.
Os pais da Matilde estão a decorar
a sua sala. Precisam de 13 rolos de papel
de parede. O papel de parede que
escolheram custa 32 € por rolo.
Quanto vão gastar com o papel de parede?
3.
O João foi almoçar com os seus pais a um restaurante que tinha vários tipos
de ementas.
Quantos almoços diferentes, incluindo apenas uma sopa e um prato, pode o João fazer?
Operações com números naturais
Uma sopa à escolha
(legumes, feijão ou canja)
Um prato à escolha
(frango, salmão, vitela
ou omeleta)
261287 012-033.indd 28 30/05/14 17:49

31. 1
29
4.
Uma família foi acampar durante uma semana. Observa o preçário do parque
de campismo.
Formula um problema com base na informação da tabela. Troca o teu problema com
o de um colega teu e resolve o problema dele.
DESAFIO Coberturas de gelado
Observa a figura seguinte.
Na geladaria da Margarida, há cinco ingredientes diferentes para pôr por cima
do gelado.
O Tiago queria decorar o seu gelado com dois ingredientes diferentes. Com quantas
combinações diferentes pode decorar o gelado?
Operações com números naturais
Preços (dia)
Adulto
Criança
Tenda
Carro
Caravana
4 €
2 €
5 €
2,5 €
9 €
1 € 1,50 € 1,20 € 1 €
1,20 €
Pepitas de chocolate
Raspa de amêndoa
Nozes
Doce de morango
Chantilly
261287 012-033.indd 29 30/05/14 17:49

32. 30
Algoritmo da multiplicação
Uma loja de artigos de informática fez
uma promoção de impressoras.
No primeiro dia vendeu 12 impressoras.
Quanto recebeu pela venda
das impressoras nesse dia?
A Maria escolheu usar o algoritmo
para calcular, mas calculou de duas
formas:
Discute com os teus colegas as formas de calcular da Maria.
2 3 9 5 18 (18 unidades). Registo
8 unidades e sobra 1 dezena.
2 3 4 5 8 (8 dezenas). Junto 1 dezena que
tinha sobrado e ponho 9.
1 3 9 5 9 (9 dezenas). Ponho 90.
1 3 4 5 4 (4 centenas). Ponho 4 centenas.
Uma forma Outra forma
4 9
3 1 2
9 8
1 4 9 0
5 8 8
4 9
3 1 2
1 8
8 0
9 0
1 4 0 0
5 8 8
1. Efetua as operações seguintes.
a) 36 3 8 c) 128 3 4 e) 93 3 16
b) 45 3 14 d) 62 3 27 f) 273 3 52
CALCULADORA produtos curiosos
Usa a calculadora para obteres os resultados de:
1 3 999 4 3 999
2 3 999 5 3 999
3 3 999
Observa com atenção os produtos obtidos. O que verificas?
Calcula mentalmente:
6 3 999 5 8 3 999 5
7 3 999 5 9 3 999 5
Operações com números naturais
261287 012-033.indd 30 30/05/14 17:49

33. 31
RESOLUÇÃO DE PROBLEMAS
1
1.
Após uma viagem do comboio Intercidades do Porto para Lisboa, o revisor reparou que não
anotara quantos passageiros tinham entrado no Porto. Em baixo estão os seus registos.
CALCULADORA o maior e o menor produto
Usa a calculadora e descobre o maior e o menor produto.
No teu caderno coloca, sem repetires, os algarismos 1, 2, 3, 4 e 5 nos quadrados,
de forma a obteres:
o maior produto:
o menor produto:
Experimenta com outros conjuntos de cinco algarismos.
Existirá alguma regra para obter o maior produto? E para obter o menor produto?
3
a) Descobre quantas pessoas entraram no Porto.
b)
Dos passageiros que entraram em Aveiro, 18 vão para Santarém. Se o bilhete
Aveiro-Santarém custa 23 €, quanto pagaram esses passageiros no total?
c) Formula outro problema com os dados da tabela.
2.
Um chuveiro normal de duche gasta aproximadamente 13 litros de água por minuto.
O João toma todos os dias um duche de 15 minutos.
Quantos litros de água poupa numa semana se, em cada dia, demorar apenas 10
minutos no duche?
3
Operações com números naturais
Estações Entraram Saíram
Porto ? 0
Aveiro 27 12
Coimbra 45 24
Pombal 14 5
Santarém 25 22
Lisboa 0 208
261287 012-033.indd 31 30/05/14 17:49

34. 32
REVISÃO
1. Calcula mentalmente o resultado de cada uma das operações seguintes.
2.
O pai do Guilherme quer vedar
o seu terreno com rede.
Observa a planta do terreno.
Cada quadrado pequeno representa
um pilar.
a)
Quantos metros de rede são
necessários?
b)
Se cada metro de rede custar 21 €
e cada pilar custar 14 €, quanto vai
gastar o pai do Guilherme?
3. Observa a seguinte reta numérica:
a)
Faz a correspondência entre cada um dos números indicados em baixo e a posição
assinalada por uma letra na reta numérica.
154 000 — 212 000 —
197 000 — 218 000 —
4.
A avó da Francisca nasceu a 1 de janeiro de 1948 e casou-se em 1971. A mãe
da Francisca nasceu quando a avó tinha 24 anos.
35 metros
37 metros
9 metros
14
metros
26
metros
420 1 170 14 3 10 22 3 5 2000 2 1350
59 3 100 2500 2 2199 445 1 355 500 2 389
4000 2 3280 18 3 20 10 500 2 7500 8 3 1000
A avó nasceu A avó casou-se
1948 1971
a) Que idade tem agora a avó da Francisca?
b) Quantos anos tinha quando se casou?
c) Em que ano nasceu a mãe da Francisca?
d) A avó da Francisca tinha 55 anos quando a Francisca nasceu.
Em que ano nasceu a Francisca?
A B C D
150 000 160 000 170 000 180 000 190 000 200 000 210 000 220 000 230 000
261287 012-033.indd 32 30/05/14 17:49

35. 33
1
5.
A Maria vai organizar uma festa e resolveu servir sanduíches. Para fazer as sanduíches,
comprou:
presunto, fiambre, mortadela, salame e queijo flamengo;
três tipos de pão: pão de forma, pão integral e pão de centeio.
Quantos tipos de sanduíches diferentes, cada uma só com um ingrediente para além
do pão, pode servir?
6. Copia para o teu caderno e completa.
7.
Descobre os números e, no teu caderno, substitui cada letra pelo número correto.
8.
Completa a tabela. Estima o valor dos seguintes produtos aproximando um dos fatores
à dezena mais próxima.
Número Estou entre Sou múltiplo de Sou múltiplo de
A 70 e 100 6 7
B 100 e 200 10 9
C 110 e 130 12 8
D 110 e 140 11 6
E 200 e 300 20 11
5
38 2150
310 310
32
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
É próximo de... Estimativa
14 3 19
11 3 25
21 3 14
69 3 11
43 3 19
31 3 12
261287 012-033.indd 33 30/05/14 17:49

36. 34
2
UNIDADE
A escola da Mara organizou uma visita de estudo. Vão 243 pessoas
(alunos, professores e funcionários). Os autocarros disponíveis têm
50 lugares. Quantos autocarros são necessários? Explica como
chegaste à tua resposta.
261287 034-053.indd 34 30/05/14 17:50

37. 35
Divisão
1.
Os professores prepararam uma surpresa para os 228 alunos. Durante a viagem vão
distribuir rebuçados!
a)
Os rebuçados que escolheram são vendidos em embalagens de 20.
Quantas embalagens têm de comprar para distribuir um rebuçado a cada menino?
Explica como pensaste.
b)
Fazendo esta distribuição, sobra algum rebuçado?
c)
Quantas embalagens terão de comprar se quiserem distribuir dois rebuçados a cada
menino? Explica como chegaste à tua resposta.
2.
A viagem demorou cerca de 4 horas, no percurso de ida e volta. Sabendo que cada
autocarro percorreu 340 km, quantos quilómetros fez, em média, por hora?
10 MINUTOS
Observa as igualdades.
Usa a mesma estratégia de cálculo mental para resolveres as operações seguintes.
48 : 4 52 : 4 80 : 16 120 : 8
: 2
: 2
24 : 4 5 12 : 2 5 6 : 1 5 6
Operações com números naturais
261287 034-053.indd 35 30/05/14 17:50

38. 36
3.
O pai do Tiago quer comprar uma televisão nova. Foi a uma loja e na montra viu dois
modelos diferentes.
Compara os preços dos dois modelos. Quantos LCD's poderás comprar com o valor
de um LED?
4.
Na escola do Gonçalo, o professor de música vai ensaiar um coro para cantar na festa
de Natal. Estão inscritos 41 alunos de toda a escola. O professor quer organizar
os alunos por filas. Cada fila deverá ter 9 alunos.
a) Quantas filas de 9 alunos poderão ser formadas?
b)
Os restantes alunos ficarão à frente. Quantos alunos colocará o professor de música
à frente?
c)
Na plateia organizaram-se as 180 cadeiras disponíveis em 15 filas com o mesmo
número de cadeiras. Quantas cadeiras tem cada fila?
Operações com números naturais
Divisão
261287 034-053.indd 36 30/05/14 17:50

39. 37
2
5. Observa a planta da sala de aula da Maria.
Na planta, a Maria só desenhou alguns mosaicos, junto do lado maior. Contudo, viu
que o chão está coberto com 280 mosaicos quadrados. Quantos mosaicos estão junto
do lado menor? Explica como pensaste.
6.
Numa festa estavam 4 rapazes e algumas raparigas.
Todos os rapazes dançaram com todas as raparigas
e formaram no total 12 pares diferentes. Quantas
raparigas eram?
Operações com números naturais
10 MINUTOS
Calcula mentalmente.
14 : 2
14 3 0,5
28 : 2
28 3 0,5
56 : 2
56 3 0,5
22 : 2
22 3 0,5
44 : 2
44 3 0,5
88 : 2
88 3 0,5
261287 034-053.indd 37 30/05/14 17:50

40. 38
Multiplicação e divisão
Operações com números naturais
1.
A Mariana viu uns cadernos muito bonitos. Cada caderno custa 1,50 €.
a)
Para comprar 9 cadernos, que quantia tinha de ter a Mariana?
b)
Quantos cadernos se podem comprar com 18 €? Explica como pensaste.
c)
E com 24 €? Porquê?
d)
E com 45 €? Explica como pensaste.
2. Completa, como no exemplo:
a) 24 : 2 5 12 porque 12 3 2 5 24
b) : 3 5 25 porque 25 3 3 5
c) 120 : 5 40 porque 40 3 5 120
d) 90 : 5 15 porque 3 5
e) : 4 5 50 porque 3 5
f) : 9 5 30 porque 3 5
3. Completa as operações com um dos divisores seguintes.
: 2 : 3 : 4 : 5 : 6 : 7 : 8 : 9
360 5 120 84 5 12 440 5 55
342 5 171 189 5 21 232 5 58
105 5 21 126 5 21 220 5 44
966 5 483 484 5 121 117 5 13
a)
Que estratégias usaste para descobrir o divisor correto? Partilha-as com os teus colegas.
1,50€ 1,50€ 1,50€
Preço dos cadernos
1 caderno 1,50 €
2 cadernos 3 €
4 cadernos 6 €
261287 034-053.indd 38 30/05/14 17:50

41. 39
2
Operações com números naturais
4.
Na frutaria da D. Maria, as laranjas vão ser expostas para venda em caixas idênticas
à da figura.
a) Com 36 laranjas, quantas caixas se enchem?
b) E com 72 laranjas?
c) E com 90 laranjas?
d) E se forem 18 laranjas?
e) E se forem 135 laranjas?
Nesta situação, o número de laranjas por
caixa é sempre o mesmo, mas o número
total de laranjas varia.
f)
Encontras alguma relação entre o número de laranjas a arrumar e a quantidade
de caixas necessária para o fazer?
5.
Para arrumar melhor a fruta, a D. Maria escolheu comprar caixas com capacidade para
4, 8 e 16 laranjas.
10 MINUTOS
Calcula mentalmente, usando a estratégia do exemplo:
490 : 5 5 490 : 10 3 2 5 49 3 2 5 98
450 : 5
340 : 5
650 : 5
760 : 5
a)
Para um total de 144 laranjas, quantas caixas vão ser necessárias:
se usarmos apenas caixas de 4 laranjas?
se usarmos apenas caixas de 8 laranjas?
se usarmos apenas caixas de 16 laranjas?
Nesta situação, o número de laranjas a distribuir é sempre o mesmo, mas
o tamanho das caixas muda.
b)
Como podes relacionar a quantidade de laranjas que cada caixa pode levar com
a quantidade de caixas necessária para distribuir as 144 laranjas?
261287 034-053.indd 39 30/05/14 17:50

42. 40
Calculando em cadeia
1. Copia para o teu caderno e calcula em cadeia.
Operações com números naturais
4 : 2 5
8 : 2 5
16 : 2 5
32 : 2 5
64 : 2 5
128 : 2 5
8 : 4 5
16 : 4 5
32 : 4 5
64 : 4 5
128 : 4 5
256 : 4 5
64 : 2 5
64 : 4 5
64 : 8 5
64 : 16 5
64 : 32 5
64 : 64 5
400 : 5 5
200 : 5 5
100 : 5 5
50 : 5 5
25 : 5 5
400 : 10 5
200 : 10 5
100 : 10 5
50 : 10 5
25 : 10 5
80 : 40 5
80 : 20 5
80 : 10 5
80 : 5 5
80 : 2,5 5
120 : 4 5
200 : 4 5
260 : 4 5
44 : 4 5
38 : 4 5
90 : 4 5
320 : 4 5
420 : 4 5
620 : 4 5
900 : 4 5
2200 : 4 5
2440 : 4 5
Discute com os teus colegas as estratégias que utilizaste.
2. Calcula em cadeia.
Discute com os teus colegas as estratégias que utilizaste.
3. Como posso calcular rapidamente 84 : 4? Observa como pensou o Tiago.
Calcula o resultado de cada uma das operações utilizando a mesma estratégia.
84 : 4 5 ?
Sei que metade de 84 é 42.
E metade de 42 é 21, então,
fiz: 84 : 2 5 42; 42 : 2 5 21
261287 034-053.indd 40 30/05/14 17:50

43. 41
2
Discute com os teus colegas como terá calculado a Joana metade de 650.
Sabendo que 500 : 2 5 250, calcula rapidamente 590 : 2.
Explica como pensaste.
Calcula mentalmente.
340 : 2 850 : 2 982 : 2
Operações com números naturais
10 MINUTOS
Para cada uma das seguintes sequências determina uma possível regra de formação e,
de acordo com essa regra, escreve os três números seguintes.
160 80 40
240 120 60
3,2 1,6 0,8
4,8 2,4 1,2
14,4 7,2 3,6
4. Calcula mentalmente.
284 : 2
390 : 2
550 : 2
4600 : 4
720 : 4
1200 : 10
790 : 10
2500 : 100
35 000 : 1000
150 3 10
27 3 100
48 3 1000
investiga decompor para dividir
A Joana pensou numa estratégia diferente para fazer alguns cálculos.
Repara no que ela está a pensar.
Para calcular a metade de 650,
pensei:
na metade de 600;
na metade de 50…
261287 034-053.indd 41 30/05/14 17:50

44. 42
Divisores de um número natural
O João ofereceu à sua mãe 12 túlipas vermelhas,
no seu aniversário. Mais tarde, ficou a pensar
nas várias formas de distribuir as túlipas por jarras,
se a mãe colocasse o mesmo número de túlipas
em cada jarra.
O João achava que existiam várias
soluções.
1. Agora, responde.
a)
Quantas formas diferentes de distribuir as túlipas encontrou o João?
b)
Porque não registou ele a hipótese de distribuir as túlipas por 5 jarras?
Explica como pensaste.
c)
E porque não registou a possibilidade de as pôr em 7 jarras?
Primeiro verificou que podia repartir as 12 túlipas por 12 jarras e assim ficava uma
túlipa em cada jarra.
Depois pensou na hipótese de colocar 2 túlipas em cada jarra e viu que era possível.
Então, para não se esquecer de nenhuma hipótese, resolveu organizar uma tabela.
Número de túlipas Número de jarras
Número de túlipas
em cada jarra
12 12 12 : 12 5 1
12 6 12 : 6 5 2
12 4 12 : 4 5 3
12 3 12 : 3 5 4
12 2 12 : 2 5 6
12 1 12 : 1 5 12
12 3 1 5 12
6 3 2 5 12
4 3 3 5 12
3 3 4 5 12
2 3 6 5 12
1 3 12 5 12
Não te esqueças!
O 12 só pode ser dividido, com quociente inteiro e resto zero, por 12, 6, 4, 3, 2
ou 1; então, dizemos que estes números são divisores de 12, ou que dividem 12.
Repara que podes encontrar os divisores de 12 escrevendo o 12 como produto
de 2 fatores.
Números naturais
261287 034-053.indd 42 30/05/14 17:50

45. 43
2
2. Indica todos os divisores de:
a) 5 c) 8 e) 10
b) 16 d) 21 f) 75
3.
Uma caixa tem 30 palitos. Vamos imaginar que queremos usá-los todos para representar
lados de polígonos. Diz se conseguimos formar:
a) só triângulos; d) só hexágonos;
b) só quadrados; e) só heptágonos.
c) só pentágonos;
4.
Como podemos embalar 45 bombons de modo que fique o mesmo número de bombons
em cada embalagem?
5.
Das afirmações seguintes, indica as que são verdadeiras e as que são falsas.
Justifica, em cada caso, a tua opção.
a) O número 2 é divisor de todos os números pares.
b) O número 3 é divisor de todos os números ímpares.
c) Existe um número que é divisor de todos os números.
d) Qualquer número diferente de 1 tem, pelo menos, dois divisores.
6. Que número sou eu?
Sou um número ímpar de 3 algarismos.
O meu algarismo das dezenas é um divisor par de 6.
A soma dos meus algarismos das unidades e das dezenas é 5.
O meu algarismo das centenas é divisor de qualquer número.
DESAFIO Dividindo maçãs
Descobre quantas maçãs tem o Gonçalo,
sabendo que:
tem menos de 30 maçãs;
se as dividir igualmente por 5 sacos,
sobram 2 maçãs;
se as dividir igualmente por 8 sacos,
sobram 6 maçãs.
Números naturais
261287 034-053.indd 43 30/05/14 17:50

46. investiga Relações entre múltiplos e divisores
44
A Joana quer saber se os divisores de 6 também dividem os múltiplos de 6.
Investiga tu também.
Encontra agora os divisores de 8. Verifica se esses divisores dividem os múltiplos de 8.
Testa as tuas descobertas com outros números e escreve-as.
A Joana ficou muito entusiasmada com as suas descobertas e decidiu investigar
se existe alguma relação entre os múltiplos de um número e os múltiplos dos seus
divisores.
Em grupo, volta a registar os primeiros seis múltiplos de 6.
Calcula agora os primeiros seis múltiplos de cada um dos divisores de 6 e circunda
os que são múltiplos de 6. O que observas?
Investiga agora com os múltiplos e divisores de 8, 9 e 10.
A Joana está a investigar os divisores e os múltiplos de 6.
O 6 só tem quatro
divisores, que são:
1, 2, 3 e 6. Mas tem muitos
múltiplos!
6, 12, 18, 24, 30, 36, …
10 MINUTOS
Em cada caso, regista a resposta correta: A, B, C ou D.
É divisor de 16:
A — 3 B — 6 C — 8 D — 32
É divisor de 45:
A — 10 B — 15 C — 25 D — 90
Não é divisor de 18:
A — 1 B — 3 C — 6 D — 12
Números naturais
Divisores de um número natural
261287 034-053.indd 44 30/05/14 17:50

47. 45
2
Operações com números naturais
Divisão inteira
A Filipa foi brincar com as suas três melhores amigas e levou um saco com 25 rebuçados.
Se distribuir os rebuçados igualmente entre ela e as amigas, com quantos rebuçados fica
cada uma?
O João pensou assim:
1. Observa e completa, como no exemplo.
Não te esqueças!
Numa divisão inteira, o dividendo (D) é igual ao produto do divisor (d) pelo quociente
(q) mais o resto (r).
D 5 d 3 q 1 r
Dividendo Divisor Quociente Resto
51 5 10 1
46 5 9 ?
53 10 ? ?
82 4 ? ?
? 20 11 0
2.
A empresa da D. Mariana faz lembranças para vários tipos de festas. Para
uma encomenda, teve de cortar 145 tiras de fita com 5 cm de comprimento.
No rolo só ficaram 75 cm de fita. Quanto media no total a fita?
Tenho de repartir 25 por 4:
25 : 4
Sei que 6 3 4 5 24, então, cada
uma fica com 6 rebuçados
e sobra 1 rebuçado:
25 5 6 3 4 1 1
10 MINUTOS
Completa.
125 : 5 25 3 7 5 105 80 : 5 20
12 3 5 60 : 6 5 15 3 11 5 198
261287 034-053.indd 45 30/05/14 17:50

48. RESOLUÇÃO DE PROBLEMAS
46
1.
Observa as imagens seguintes. Os livros têm todos o mesmo preço e as canetas têm
todas o mesmo preço.
Operações com números naturais
4
1
a) Se a mãe da Rita quiser comprar 6 canetas iguais às deles, quanto terá de pagar?
b) Qual foi o preço de cada livro?
c) Explica como chegaste às tuas respostas.
2.
Copia a figura para o teu caderno e coloca os números 6, 12, 15, 24, 41, 72, 90 e 246
nos setores vazios do decágono, de modo que, dados dois quaisquer números opostos,
o quociente entre o maior e o menor seja 6.
3.
Uma fotocopiadora tira 50 cópias por minuto. A D. Elsa tem de fotocopiar uma ficha
de trabalho com 3 páginas para 5 turmas da escola. Sabendo que cada turma tem
25 alunos, conseguirá a D. Elsa fazer as cópias em 10 minutos?
a) Explica como pensaste.
A Rita pagou 25 €
por 3 livros e 2 canetas.
O João comprou 3 livros
e 1 caneta iguais aos dela
e pagou 23 €.
261287 034-053.indd 46 30/05/14 17:50

49. 2
47
Operações com números naturais
Sabendo que tem de cobrir um retângulo de 60 cm por 45 cm, qual dos valores a seguir
indicados poderá ser a medida do lado dos quadrados?
4 cm 5 cm 6 cm 7 cm
Explica como chegaste à tua resposta.
5.
O João queria saber a altura de água do poço do seu avô. Pendurou um balde na corda
que estava presa à manivela e observou que por cada volta da manivela o balde descia
50 cm no interior do poço.
Iniciando com a corda totalmente enrolada,
verificou ainda que o balde atingia a superfície
da água depois de dar 6 voltas à manivela
e que chegava ao fundo ao fim de 14 voltas.
a)
Que altura de água existia no poço?
b)
Explica como chegaste à tua resposta.
4.
A mãe da Joana gosta muito de fazer bricolagem e comprou um bonito tabuleiro de chá,
que gostaria de cobrir com um padrão de quadrados pretos e brancos alternados.
6.
O cão da Gabriela come 150 g de ração por dia. Os pais da Gabriela
compram a ração em embalagens de 1 kg. Quantas embalagens terão
de comprar para o mês de novembro de modo a garantir que não falta ração
para alimentar o cão?
Explica como pensaste e partilha a tua estratégia com os teus colegas.
261287 034-053.indd 47 30/05/14 17:50

50. 48
Algoritmo da divisão
A Joana fez 9 anos e convidou 24 amigos para a sua festa de aniversário.
A mãe da Joana comprou 152 balões e deu o mesmo número de balões a cada um deles.
Quantos balões deu a cada amigo? Sobraram balões?
Observa como o Francisco pensou para encontrar a resposta.
Operações com números naturais
10 MINUTOS
Calcula em cadeia mentalmente.
Se são 24 amigos, vou tentar
descobrir qual é o número que
multiplicando por 24 dá um
produto próximo de 152.
1. Calcula:
a) 184 : 61 b) 298 : 72 c) 115 : 55 d) 132 : 31
1 3 12 4 3 12
10 3 12 8 3 12
5 3 12 7 3 12
2 3 12 9 3 12
1 3 23 4 3 23
10 3 23 8 3 23
5 3 23 7 3 23
2 3 23 9 3 23
1 3 15 4 3 15
10 3 15 8 3 15
5 3 15 7 3 15
2 3 15 9 3 15
1 3 24 5 24
2 3 24 5 48
3 3 24 5 72
4 3 24 5 96
5 3 24 5 120
6 3 24 5 144
D£escobrı $q†e |å |m˜åe $∂e† |å |cadå $amigo 6 $bal∏Ƨ.
1 5 2
2 1 4 4
8
24
6
S∞obraµ
8 $bal∏Ƨ.
261287 034-053.indd 48 30/05/14 17:50

51. 49
2
Operações com números naturais
O Sr. Afonso colheu este ano 913 kg de batatas. Calcula quantos sacos poderá encher
sabendo que cada um leva 35 kg.
Observa com atenção a resolução do Miguel.
2. Calcula:
a) 144 : 13 c) 326 : 27 e) 549 : 32
b) 768 : 63 d) 947 : 43 f) 1395 : 87
3.
Os 169 alunos de uma escola vão ver uma peça de teatro. Só foi possível alugar uma carrinha
de 14 lugares. Quantas viagens tem de fazer a carrinha para levar todos os alunos ao teatro?
9 1 3
2 7 0 0
2 1 3
2 1 7 5
3 8
2 3 5
3
913 ≈ 35
3 5
2 0
1 5
1 1
2 6
1 3 35 5 35 (¢Ë $poucø)
10 3 35 5 350
100 3 35 5 3500 (¢Ë muitø)
20 3 35 5 700 ($dobrø $∂ 10 3 35)
5 3 35 5 175 (µeta∂ $∂ 10 3 35)
N∞úµerø $∂ $saco§ $q† $ø S∞®. A∞fonsø vaı
¢encˇe®.
S∞obraµ 3 $k˙ $∂ $batata§.
10 MINUTOS
Resolve os números-cruzados seguintes.
Horizontais
A — 128 : 4; 3 3 25
B — Divisor de 8; 200 : 100; 50 : 10
C — 500 : 4
D — Divisor de 32; 88 : 4
E — 2,5 3 10; 150 : 3
Verticais
A — 340 : 10; divisor de 12 e 24
B — Múltiplo de 2; 3 3 55
C — 110 : 5
D — Divisor de 7; 1050 : 2
E — 550 : 10; quinta parte de 100
A B C D E
A
B
C
D
E
261287 034-053.indd 49 30/05/14 17:50

52. 50 Operações com números naturais
Algoritmo da divisão
No aviário do Sr. João produziram-se 518 ovos num dia. Quantas embalagens de 12 ovos
foi possível encher?
Repara como pensou o Tiago.
518 : 12
518
2 48
3
12
4
1. Calcula:
a) 375 : 12 5 b) 483 : 23 5 c) 182 : 25 5 d) 236 : 75 5
Reparti 51 dezenas por 12.
51 : 12 é próximo de 4, porque 4 3 12 5 48
Retiro as 48 dezenas. Sobram 3 dezenas.
Para continuar, baixei o 8, obtendo, assim,
38 unidades (38 ovos que ainda falta repartir).
38 : 12 é próximo de 3, porque 3 3 12 5 36
Retirando as 36 unidades restam 2 unidades.
518
2 48
38
2 36
2
12
43
Produziram-se 43 embalagens de ovos e sobraram 2 ovos.
10 MINUTOS
Em cada linha, pinta os retângulos dos números que são divisores do número destacado.
6 1 2 3 4 5 6 7 8 9
11 1 2 3 4 5 6 7 8 9
25 1 2 3 4 5 6 7 8 9
32 1 2 3 4 5 6 7 8 9
49 1 2 3 4 5 6 7 8 9
261287 034-053.indd 50 30/05/14 17:50

53. 51
2
Operações com números naturais
Uma fábrica produziu 1469 lâmpadas iguais. Sabendo que as lâmpadas foram embaladas
em conjuntos de 34, quantas embalagens se fizeram?
Observa como pensou a Beatriz.
1469 : 34
1. Calcula:
a) 582 : 7 5 b) 307 : 71 5 c) 1883 : 81 5 d) 1751 : 49 5
2.
A avó do João dividiu 492 euros pelos seus 12 netos. O neto João juntou 9 euros
à sua parte e utilizou o dinheiro para comprar o maior número possível de CD de jogos.
Sabendo que cada CD custou 15 euros, quanto dinheiro lhe sobrou?
Comecei por repartir 146 dezenas por 34.
Pensei: Em 14 quantas vezes há 3?
Há 4. Porque 4 3 3 5 12.
Coloquei 4 e fiz 4 3 34. Retiro as 136 dezenas.
Sobram 10 dezenas.
Baixei o 9 e pensei:
Em 10 quantas vezes há 3?
Há 3, porque 3 3 3 5 9.
Coloquei 3 e fiz 3 3 34.
Retirando as 102 unidades
sobram 7 unidades.
1469 34
1469
2 136
10
34
4
1469
2 136
109
2 102
7
34
43
Fizeram-se 43 embalagens e sobraram 7 lâmpadas.
261287 034-053.indd 51 30/05/14 17:50

54. 52
REVISÃO
Certo dia a professora comprou alguns e disse
à turma: «Comprei caixas de lápis e verifiquei
que são 192 lápis.»
a)
Sabendo que cada caixa traz 6 lápis, quantas
caixas comprou?
b)
Se cada caixa trouxesse 12 lápis, quantas caixas
seriam?
c)
Se fossem 24 lápis em cada caixa, quantas caixas
teríamos?
1. Completa:
a) 80 : 4 5 c) : 5 5 6 e) : 15 5 3
b) 3 6 5 30 d) : 4 5 30 f) 300 : 5 75
2.
Na sala da Filipa havia falta de lápis de cor.
Futsal Futebol Andebol Voleibol
Equipas de 5 Equipas de 11 Equipas de 7 Equipas de 6
Para cada uma das modalidades, refere quantas equipas se podem formar e quantos
alunos ficam suplentes.
4.
A turma do João está a forrar cubos que
construíram em cartão. Para forrar 20 cubos
foram necessárias 12 folhas de papel
autocolante. Quantas faces podem ser forradas
com uma folha?
Explica como pensaste.
3. Numa escola, os 84 alunos do 3.º e 4.º anos vão realizar vários torneios desportivos.
261287 034-053.indd 52 30/05/14 17:50

55. 53
2
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
5. Observa o conjunto de números seguinte.
Indica os elementos do conjunto que:
a) são divisores de 8;
b) são múltiplos de 5;
c) são divisores de 16 e de 24.
6.
A Mara e o Diogo são irmãos e estão ambos doentes. Foram ao pediatra e ele
receitou-lhes medicamentos diferentes.
A Mara vai tomar um destes comprimidos
de 8 em 8 horas.
O Diogo vai tomar uma destas cápsulas
de 6 em 6 horas.
Sabendo que ambos vão tomar até ao fim as embalagens apresentadas, quem termina
primeiro o medicamento? Explica como chegaste à tua resposta.
7. Calcula:
a) 126 : 9 b) 761 : 36 c) 477 : 17
1
10 2 8
15
24 12
4 16
3 5
6
261287 034-053.indd 53 30/05/14 17:50

56. 54
3
UNIDADE
Copia a tabela de frequências absolutas para o teu caderno e completa-a.
Representa a informação através de um gráfico à tua escolha.
Que outro gráfico poderias ter usado?
Se a professora pretender escolher à sorte um representante da turma,
entre os alunos, é mais provável ser um rapaz ou uma rapariga? Porquê?
A professora Fátima pretende saber mais sobre a atividade física praticada
pelos seus alunos. Para tal elaborou um questionário.
Depois de os alunos terem respondido fez uma tabela de frequências absolutas.
Questionário «Atividade Física»
Idade: anos
Sexo: F M
Peso: kg
Altura: cm
Normalmente fazes uma
alimentação saudável?
Sim Não
Qual é o desporto que praticas?
Quantas horas, por semana,
praticas esse desporto?
1 2 3
4 5
Sexo Contagem
Frequência absoluta
(Número de alunos)
Feminino (F) IIII IIII II
Masculino (M) IIII III
261287 054-069.indd 54 30/05/14 17:51

57. 55
Pictogramas
Representação e interpretação de dados e situações aleatórias
1.
Para que a professora Fátima possa observar
os dados e tirar conclusões sobre a atividade
física dos seus alunos da turma A do 4.º ano,
ela terá de efetuar contagens, organizar
os dados em tabelas de frequências
e apresentar os dados através de gráficos.
Estás preparado(a) para ajudar a professora
Fátima nesta tarefa?
Através da tabela de frequências seguinte,
a professora pretende construir um pictograma
para representar as idades dos alunos.
a) Completa a tabela de frequências.
Idades Contagem Frequência absoluta
8 II
9 IIII I
10 IIII IIII
11 II
Idades Legenda: 5 2 alunos
8
9
10
11
b)
Usa o quadriculado do teu caderno para construíres o pictograma seguinte
e considera que cada vale 2 alunos. Pensa num título para o pictograma.
c)
Qual é a idade mais frequente?
d)
Quantos alunos têm uma idade superior ou igual a 10 anos?
e)
Elabora duas perguntas que possam ser respondidas com a informação
do pictograma. Responde às perguntas que elaboraste no teu caderno.
261287 054-069.indd 55 30/05/14 17:52

58. 56
Gráfico de barras e gráfico de pontos
Representação e interpretação de dados e situações aleatórias
1.
Através de um gráfico de barras, a professora representou a frequência com que cada
aluno do 4.º A pratica desporto.
Observa o gráfico de barras e responde às questões no teu caderno.
a) Quantos alunos praticam desporto três horas por semana?
b) Qual é a moda, ou seja, o número de horas praticado pelo maior número de alunos?
c) Quantos alunos praticam o maior número de horas de desporto?
d)
Qual é a percentagem de alunos que praticam desporto menos de três horas por semana?
2.
Para representar os dados sobre o desporto praticado por cada um dos alunos do 4.º A,
a professora construiu um gráfico de pontos, usando cruzes.
Observa o gráfico de pontos e responde às questões no teu caderno.
0
2
Número de horas por semana
5
4
3
1
Número
de
alunos
10
8
6
4
2
Prática de desporto
Ginástica
Desporto
Natação
Atletismo
Futebol
Número
de
alunos
Desportos praticados na turma do 4.º A
X X
X
X
X
X
X
X
X
X X
X X
X
X X
X
X X
X
261287 054-069.indd 56 30/05/14 17:52

59. 57
3
Representação e interpretação de dados e situações aleatórias
a) Qual é o desporto praticado pelo maior número de alunos?
b) Há mais alunos a praticar atletismo ou a praticar natação?
c)
Completa, no teu caderno:
1
2
da turma pratica .
1
4
da turma pratica .
d)
Elabora duas questões que possam ser respondidas com base no gráfico.
e)
Representa a mesma informação através de outro tipo de gráfico à tua escolha.
f)
Indica algumas das conclusões que podes tirar relativamente ao tipo de desporto
praticado pelos alunos desta turma.
g)
Com base na informação disponível nos dois gráficos da página ao lado, é possível
afirmar que todos os praticantes de futebol praticam esta modalidade apenas à
terça-feira e à quinta-feira? Explica como pensaste.
3.
Para representar os pesos dos alunos do 4.º A, a professora recorreu novamente
a um gráfico de pontos.
Os pesos dos alunos, em quilogramas, são os seguintes:
38, 35, 29, 41, 36, 30, 31, 33, 38, 27, 29, 33, 27, 22, 41, 42, 38, 40, 25, 34
Como os valores são bastante distintos, o gráfico de pontos toma o seguinte
aspeto:
a) Qual é o maior peso observado? E o menor?
b) Há algum valor que tenha sido registado um maior número de vezes?
c)
Regista no teu caderno se as afirmações seguintes são verdadeiras (V) ou falsas (F).
50% dos alunos tem peso maior do que 30 kg.
1
4
dos alunos tem peso menor do que 30 kg.
Há mais alunos com peso inferior a 25 kg do que alunos com peso superior
a 40 kg.
20
0 25 35 45
30 40
Peso dos alunos
Peso (em kg)
Número
de
alunos
261287 054-069.indd 57 30/05/14 17:52

60. 58
Diagrama de caule-e-folhas
Representação e interpretação de dados e situações aleatórias
Na turma do 4.º A da professora Fátima, as alturas, em centímetros, também variam
de aluno para aluno. Os resultados obtidos foram:
148 132 142 150 141 128 134 126 127 145
135 138 147 129 142 138 135 138 125 137
Para fazer a análise da distribuição de alturas, a professora construiu um diagrama
de caule-e-folhas:
1.º Passo: Definiu os caules com os algarismos
das dezenas e das centenas que compõem cada
uma das medidas observadas, ordenando-os na
vertical, e desenhou um traço vertical.
2.º Passo: Foi registando, um a um, cada
número da tabela, dispondo o algarismo das
unidades (folhas) no caule correspondente. Por
exemplo, escreveu 8 à direita do caule 14, 2 à
direita do caule 13, e assim sucessivamente.
3.º Passo: Ordenou cada linha, por ordem crescente.
12 5 6 7 8 9
13 2 4 5 5 7 8 8 8
14 1 2 2 5 7 8
15 0
Caules Folhas
12 8 6 7 9 5
13 2 4 5 8 8 5 8 7
14 8 2 1 5 7 2
15 0
12
13
14
15
1.
Observa o diagrama anterior e responde às questões.
a)
Há mais alunos com altura maior do que 130 cm e menor do que 140 cm ou alunos
com altura maior do que 140 cm e menor do que 150 cm?
b) Qual é a altura do aluno mais baixo da turma? E do aluno mais alto?
c)
Há alunos com alturas iguais? Se sim, menciona-as.
d)
No início do ano letivo, a professora Fátima já tinha recolhido a informação sobre
as alturas dos alunos. Parece-te provável que os resultados obtidos agora tenham
sido os mesmos? Porquê?
e)
Seria adequado representar esta informação através de um gráfico de barras?
Explica como pensaste.
261287 054-069.indd 58 30/05/14 17:52

61. 59
3
Gráfico circular
Representação e interpretação de dados e situações aleatórias
1.
A professora apresentou, através de um gráfico circular, a informação recolhida sobre
o tipo de alimentação praticado pelos 20 alunos do 4.º A. Observa o gráfico.
Tipo de alimentação
Saudável
Não saudável
a) Quantos alunos têm uma alimentação não saudável?
b) Qual é a moda: ter uma alimentação saudável ou não saudável?
c) Analisa os comentários seguintes.
1
2
3
4
da turma tem uma
alimentação saudável.
Só
1
2
3
4
da turma tem uma
alimentação saudável.
25% da turma tem
uma alimentação
não saudável.
90% da turma tem
uma alimentação
saudável.
Quais são os meninos que estão a pensar corretamente? Porquê?
Maria
João
Bernardo Luís
261287 054-069.indd 59 30/05/14 17:52

62. 60
Diagrama de Carroll
Representação e interpretação de dados e situações aleatórias
1.
Para estudar se havia diferenças entre o tipo de alimentação seguido pelos rapazes
e pelas raparigas, a professora elaborou um diagrama de Carroll.
Alimentação
Género Saudável Não saudável
Raparigas 7 5
Rapazes 8 0
Com base no diagrama, responde às questões.
a) Quantos alunos responderam ao inquérito?
b) Indica o número de:
rapazes que não têm uma alimentação saudável;
crianças que têm uma alimentação não saudável.
c)
Há diferenças entre a alimentação das raparigas e dos rapazes desta turma? Se sim,
descreve-as e explica o teu raciocínio.
d)
A Maria e o Tiago, alunos da turma A, observaram o diagrama e conversaram sobre
os resultados.
Quem tem razão? Com esta informação, será possível tirar conclusões sobre
a alimentação de todos os alunos da escola? Ou apenas sobre a alimentação
dos alunos da turma A?
Pensa e discute a tua opinião com os teus colegas.
Muitas crianças da nossa
sala têm uma alimentação
saudável.
Mas não sei
se as crianças
das outras turmas
também têm.
261287 054-069.indd 60 30/05/14 17:52

63. 61
Frequências relativas
1.
Observa as cores dos 10 clipes representados.
a) Completa a tabela.
Representação e interpretação de dados e situações aleatórias
Cor
Frequência
absoluta
Frequência
relativa
Azul 3
10
3
Amarela
Verde
Vermelha
N.º de golos N.º de jogos
Frequência
relativa
0 5
1 3
2 4
3 8
b) Qual é a moda?
c) Qual é a percentagem de clipes que não são verdes?
2.
O Nuno todas as sextas-feiras joga futebol com os amigos. Com o registo do número
de golos marcados por jogo, ele construiu a tabela seguinte.
a) Completa a tabela.
b)
Qual é a frequência relativa dos
jogos em que não houve golos?
c)
O João afirmou que nos
primeiros 5 jogos não houve
golos. Observando apenas
a tabela, terá ele informação
suficiente para afirmar isso?
A frequência relativa
de uma categoria
é o quociente entre
a frequência absoluta
e o número total
de dados.
Não te esqueças!
3
261287 054-069.indd 61 30/05/14 17:52

64. RESOLUÇÃO DE PROBLEMAS
62
a)
Quantas flores representa cada ?
b)
Quantas flores tem o seu jardim?
c)
Regista no teu caderno duas afirmações verdadeiras usando a informação dada pelo
pictograma.
1.
Nas faturas de eletricidade recebidas
mensalmente por cada família portuguesa,
é apresentado um gráfico circular com
as fontes de energia que permitiram
a produção de eletricidade desse mês.
Observa o gráfico referente ao mês de abril
de 2010 e responde às questões.
a)
Com a ajuda da tua professora, pesquisa um pouco sobre como é produzida
a eletricidade. Procura saber um pouco mais sobre os tipos de energias renováveis
que Portugal produz.
b) Qual é a fonte de energia que mais contribuiu para a produção de eletricidade?
c)
Qual é a fonte de energia que produziu exatamente
1
4
do total?
d)
Através do gráfico consegues identificar todas as fontes de energia?
e)
Pede a um adulto uma fatura de eletricidade e vê se também apresenta a informação
sobre as fontes de energia através de um gráfico circular. Se sim, compara este
gráfico de abril de 2010 com o dessa fatura e verifica se há algumas diferenças.
Descreve-as no teu caderno.
2.
A mãe da Joana gosta muito de flores. Tem no seu jardim rosas, cravos, túlipas e jarros.
Observa o pictograma, que representa as flores do jardim da mãe da Joana. A Joana
sabe que a sua mãe tem 180 túlipas.
Flores do jardim
Rosas
Cravos
Túlipas
Jarros
Cogeração e
microprodução
P: 13,9%
Outras:
4,8%
Eólica:
25,0%
Nuclear:
3,5%
Hídrica:
27,3%
Gás natural:
14,9%
Hídrica PRE: 7,2%
Carvão: 3,4%
Fontes de energia
A eletricidade faturada foi produzida a partir das
seguintes fontes de energia
Representação e interpretação de dados e situações aleatórias
261287 054-069.indd 62 30/05/14 17:52

65. 3
63
DESAFIO um mês de desporto
Todos os dias, o João pratica um só tipo de desporto. Observa a tabela relativa
ao número de vezes em que cada desporto foi praticado, durante um mês.
a) Quantos dias é que o João:
praticou futebol? não praticou natação?
praticou natação à quinta-feira? praticou futebol e natação?
praticou atletismo ao sábado?
b) O mês em que o João fez o registo poderá ter sido o de novembro? Porquê?
c) Das seguintes afirmações, copia para o teu caderno apenas as verdadeiras:
Ao fim de semana, o João não praticou natação.
Aos domingos, o João praticou futebol ou atletismo.
2.ª-feira 3.ª-feira 4.ª-feira 5.ª-feira 6.ª-feira Sábado Domingo
Natação 2 0 2 3 1 1 0
Futebol 2 3 1 2 2 2 3
Atletismo 0 1 2 0 2 1 1
Representação e interpretação de dados e situações aleatórias
3.
Observa o gráfico, que representa a produção de uma fábrica de puzzles. O gráfico
mostra a produção de segunda-feira a quinta-feira.
a)
Quantos puzzles foram produzidos na segunda-feira?
b)
Em que dia se registou maior produção? Quantos puzzles foram produzidos nesse dia?
4.
No gráfico da tarefa 3, ainda é desconhecida a produção de sexta-feira. No entanto,
no final da semana a empresa tem de entregar uma encomenda de 1000 puzzles.
a)
Quantos puzzles terão de produzir na sexta-feira?
b)
Quantos puzzles deveriam ter produzido por dia, se produzissem sempre a mesma
quantidade diária?
c)
Com base nas duas respostas anteriores, parece-te provável que a empresa consiga
fazer a entrega completa?
200
150
100
50
0
5.ª-feira
Dias da semana
4.ª-feira
3.ª-feira
2.ª-feira
Produção de puzzles
Número
de
puzzles
261287 054-069.indd 63 30/05/14 17:52

66. RESOLUÇÃO DE PROBLEMAS
64
DESAFIO Parque de bicicletas
Para organizar uma prova de ciclismo, o Miguel e o Pedro resolveram fazer um inquérito
aos seus colegas da turma. Na tabela, estão os resultados obtidos.
a) Quantas bicicletas existem na turma? E quantas são de montanha?
b) Qual é o tipo de bicicleta mais comum? E o tipo de guiador?
c)
Quantas bicicletas têm menos de 13 velocidades?
d)
Por que razão há mais de 32 respostas nos «acessórios»?
e)
Constrói um gráfico de barras referente à cor das bicicletas.
INVESTIGA LEITURAS PREFERIDAS
Com os teus colegas, faz um estudo sobre o género de leitura preferido pelos alunos
da tua turma (aventura, ficção, poesia, ciências, BD, …). Depois de todos os alunos
registarem a sua preferência no quadro:
constrói uma tabela de frequências com a informação recolhida;
representa a informação através de um gráfico que consideres adequado;
explica como se designa esse gráfico e quais são as
razões da sua escolha.
Num pequeno texto com cinco linhas descreve
sucintamente as preferências da tua turma relativamente
ao género de leitura.
Tipo de bicicleta
Número
de velocidades
Cor da bicicleta
Tipo de guiador
Acessórios
10
12 9 11
(?)
14
8
5
7
25
8
6
12
4
5
16
Preta
Menos de 6 De 10 a 12 Mais de 12
Montanha
Resultados
A
Para-lamas
Corrida
B
Luzes
BMX
C
Bomba
Outros
Outros
Cantil
4
Prateada
5
Vermelha
6
Azul
7
Outras
Representação e interpretação de dados e situações aleatórias
261287 054-069.indd 64 30/05/14 17:52

67. 65
Todos os dias ouvimos comentários sobre:
Acontecimentos em que há a certeza de que vão ocorrer — acontecimentos certos.
3
Representação e interpretação de dados e situações aleatórias
Situações aleatórias
Acontecimentos que podem ocorrer ou não — acontecimentos possíveis ou prováveis.
Destas situações, umas são mais prováveis do que outras.
Acontecimentos que nunca ocorrem — acontecimentos impossíveis.
Hoje é provável que chova,
está bastante vento e frio.
Se lançar um dado, a face voltada para cima terá
um número de pintas igual a 1, 2, 3, 4, 5 ou 6.
É provável que, tal como
hoje, amanhã esteja sol.
É muito provável que o João
ganhe.
Por exemplo, sair 7 pintas no lançamento
de um dado.
Não te esqueças!
0% 50% 100%
Acontecimento
pouco provável
Acontecimento
impossível
Acontecimento
muito provável
Acontecimento
certo
261287 054-069.indd 65 30/05/14 17:52

68. 66
3.
Com base na tabela da tarefa 2. d), responde às questões.
a)
Saiu alguma vez uma bola castanha?
b)
Que cores saíram menos vezes? E mais vezes?
c)
O que podes concluir? Compara os resultados com os dos teus colegas.
4.
A Maria e o João querem fazer um jogo com a roleta.
a)
Eles fizeram algumas afirmações. Sublinha as que consideras verdadeiras.
É muito provável sair um múltiplo de 8.
É mais provável sair um múltiplo de 3
do que sair um número ímpar.
É igualmente provável sair um número par
ou sair um número ímpar.
Sair um número maior do que 8
é um acontecimento impossível.
1.
Discute com os teus colegas os acontecimentos seguintes e classifica cada um deles
como «impossível», «pouco provável», «muito provável» ou «certo».
Na serra da Estrela, vai nevar no inverno.
A Guarda vai atingir temperaturas de 50 ºC no inverno.
Jogar um dado e sair um número inferior a 7.
Tirar uma pastilha de um saco só com rebuçados.
Para a semana, a Joana vai ganhar no Euromilhões.
2.
Coloca num saco bolas iguais exceto na cor: duas bolas verdes, uma azul e uma vermelha,
tal como no saco da figura.
a)
Se retirasses, à sorte, uma bola do saco,
qual seria a cor mais provável dessa bola? Porquê?
b)
Tirar uma bola cor de laranja é um acontecimento possível?
c)
Retira do saco uma bola à sorte e regista a sua cor. Volta
a colocar a bola no saco. Repete esta experiência vinte
vezes.
d)
Completa a tabela com as cores que observaste.
Representação e interpretação de dados e situações aleatórias
Situações aleatórias
Cor da bola Número de vezes que saiu
Vermelha
Verde
Azul
261287 054-069.indd 66 30/05/14 17:52

69. 67
3
Representação e interpretação de dados e situações aleatórias
b)
O jogo consiste em jogar a roleta duas vezes e registar os dois números que saíram.
A Maria ganha se a soma dos números registados for par e o João ganha se a soma for
ímpar.
Quem achas que tem maior probabilidade de ganhar?
Para descobrires se tens razão, completa a tabela seguinte com todas as possibilidades
que podem ocorrer.
1 1 2 3 4 5 6 7 8
1 2 3
2 3 4
3 4
4
5
6
7
8
O que podes concluir?
INVESTIGA bolas numeradas
Observa a imagem.
Dois irmãos, o António e a Maria, receberam um puzzle e decidiram fazer um jogo
para ver quem brincaria com o puzzle primeiro.
Cada um deles vai colocar as suas quatro bolas no seu saco e, sem olhar, retirar uma.
Combinaram as seguintes regras:
Será este jogo justo?
Estuda, com recurso a uma tabela, todas as possibilidades que podem ocorrer.
Eu brinco primeiro
se o produto dos dois
números for par.
E eu brinco primeiro
se o produto dos dois
números for ímpar.
261287 054-069.indd 67 30/05/14 17:52

70. 68
1.
Numa turma registou-se, durante uma semana, o número de crianças que chegaram
à escola acompanhadas pelos avós.
REVISÃO
Crianças acompanhadas pelos avós
2.ª-feira
3.ª-feira
4.ª-feira
5.ª-feira
6.ª-feira 5 2 crianças
Associa corretamente:
Acontecimentos Classificação
Obter um cartão com número inferior a 10. Acontecimento muito provável
Obter um cartão com número inferior a 1. Acontecimento impossível
Obter um cartão com o número 1. Acontecimento certo
Obter um cartão com número superior a 2. Acontecimento pouco provável
a) Quantas crianças chegaram à escola acompanhadas pelos avós na segunda-feira?
b)
Em que dias chegaram menos crianças à escola acompanhadas pelos avós?
c)
Com base no pictograma, poderemos concluir que, durante todo o ano, é à segunda-
-feira que os avós mais acompanham os netos na ida para a escola? Explica como
pensaste.
d)
Elabora um gráfico de barras relativo ao número de crianças que chegaram à escola
acompanhadas pelos avós, nesta semana.
2.
A Joana colocou numa mesa nove cartões numerados de 1 a 9, voltados para baixo.
Ela vai tirar um cartão à sorte.
261287 054-069.indd 68 30/05/14 17:52

71. 69
3
3.
O gráfico seguinte, retirado de uma fatura da EDP, mostra a faturação mensal,
em euros, correspondente ao consumo de energia elétrica, ao longo do ano de 2009,
em casa de uma família.
48
24
0
J F M A M J J A S O N D
Gráfico de faturação (euros)
Meses
Faturação
(em
euros)
a) Indica o mês em que se registou maior consumo.
b)
No mês de julho o consumo de eletricidade desta família baixou significativamente.
Sugere uma possível razão para explicar esta descida.
c)
Supondo que o gasto médio diário é de 1,21 euros, qual é o gasto mensal (30 dias)
previsto para esta família?
d)
A partir da observação do gráfico, escreve duas frases sobre o consumo
de eletricidade desta família.
4.
A Maria recebeu uma caixa de rebuçados embrulhados em papéis com cores diferentes:
amarelos, verdes e vermelhos. Observa a imagem.
a)
Se a Maria tirar à sorte um rebuçado
da caixa, qual é a cor mais provável?
E a menos provável? Explica como
pensaste.
b)
Será possível sair um rebuçado embrulhado
em papel cor-de-rosa? Porquê?
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
261287 054-069.indd 69 30/05/14 17:52

72. 70
4
UNIDADE
Observa a cidade e regista o nome de:
sólidos que pareçam:
— poliedros;
— não poliedros.
figuras geométricas que pareçam:
— polígonos;
— não polígonos.
261287 070-091.indd 70 30/05/14 17:53

73. 71
Sólidos geométricos
Figuras no plano e sólidos geométricos
1.
Na figura, palhinhas ligadas com plasticina representam as arestas de dois prismas e os
lados de um pentágono.
O cubo e os outros paralelepípedos são prismas.
Quando as bases de um prisma são retângulos, dizemos que o prisma é um
paralelepípedo. Quando as 6 faces são retângulos, dizemos que é um
paralelepípedo retângulo.
Quando as faces de um prisma são todas quadrados, dizemos também que
o prisma é um cubo.
Não te esqueças!
a)
Completa a tabela.
Prisma
triangular
Prisma
quadrangular
Prisma
pentagonal
Prisma
hexagonal
Polígono da base
N.º de faces 5 6 7 8
N.º de arestas 9 12
N.º de vértices 6 8
b)
Descobre qual é a relação que existe entre:
o número de lados do polígono da base e o número de faces de cada prisma;
o número de lados do polígono da base e o número de arestas de cada prisma;
o número de lados do polígono da base e o número de vértices de cada prisma.
2.
Quais são os números de faces, de arestas e de vértices de um cubo?
E de um paralelepípedo?
261287 070-091.indd 71 30/05/14 17:53

74. 72 Figuras no plano e sólidos geométricos
Prismas retos
1. Estes poliedros são prismas retos. Repara no que têm em comum.
a)
Completa as frases de acordo com as características dos prismas retos, utilizando
as palavras do quadro.
Repara que decompondo o cubo e o paralelepípedo retângulo, como mostra a figura,
se obtém, em cada caso, dois prismas triangulares retos.
A
D
B
E
C
F
As arestas laterais têm
o mesmo
e são
As bases são
geometricamente iguais situadas
em planos
As faces laterais são
retângulos
comprimento
paralelas
polígonos
paralelos
b)
Escreve o nome de todos os prismas retos representados em 1.
A B C
D E F
261287 070-091.indd 72 30/05/14 17:53

75. 73
4
Figuras no plano e sólidos geométricos
Planificações
1. Observa as planificações e assinala as que correspondem a planificações de prismas retos.
INVESTIGA Planificações do cubo
O Pedro e a Catarina quando estudavam os sólidos geométricos decidiram construir
alguns observando os modelos e começaram por fazer o cubo. Sabiam que tinha
6 faces quadradas e fizeram
o seguinte:
Recortaram e tentaram dobrar mas não conseguiram construir o cubo.
Tenta tu construir a planificação de um cubo.
Usando papel vegetal copia os modelos seguintes, recorta-os e verifica se são
planificações do cubo. Também podes utilizar polidrons, se existirem na tua escola.
a) b) c) d) e)
Investiga outras planificações do cubo.
261287 070-091.indd 73 30/05/14 17:53

76. 74 Figuras no plano e sólidos geométricos
1. Responde:
a) Se te perguntassem o que é uma circunferência, o que dirias?
b) Como defines «círculo»?
c)
Observa a tua sala de aula. Dá exemplos de objetos em forma de círculo
ou de circunferência.
Círculo e circunferência
A Maria e a Marta estão a fazer desenhos usando latas.
Desenho da Maria Desenho da Marta
Maria Marta
A Maria desenhou uma circunferência e a Marta desenhou um círculo.
Os nossos desenhos
são iguais.
Não concordo. Tu desenhaste
só o contorno e eu desenhei
o contorno e o interior.
261287 070-091.indd 74 30/05/14 17:53

77. 75
4
Figuras no plano e sólidos geométricos
Raio e diâmetro
João Pedro
Essa distância chama-se raio e é igual
ao comprimento do fio que o jardineiro
José usou. Cada segmento de reta que
una um ponto da circunferência com
o centro também se chama raio.
O jardineiro José está a construir um canteiro com a forma de um círculo.
Repara que colocou uma estaca e usou um fio esticado para construir uma circunferência.
O jardineiro José usando fio azul esticado uniu dois pontos da circunferência passando pelo
centro. O comprimento desse fio é o dobro do raio e chama-se diâmetro. Cada segmento
que una dois pontos opostos da circunferência também se chama diâmetro.
Todos os pontos da
circunferência estão à mesma
distância da estaca (centro).
261287 070-091.indd 75 30/05/14 17:53

78. 76
1.
Observa os três círculos apresentados na figura e, no teu caderno, constrói e completa
a tabela.
Figuras no plano e sólidos geométricos
Raio e diâmetro
A
0 15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
B C
2.
Para desenhar círculos e circunferências, podemos
utilizar o compasso.
Abre o teu compasso com uma abertura de 2 cm.
Mantendo essa abertura desenha uma circunferência
no teu caderno.
a)
A medida da abertura do compasso corresponde à medida do raio ou do diâmetro?
b) Faz medições e verifica a tua resposta.
DESAFIO circunferências
Qual é o diâmetro da circunferência maior representada na figura?
Explica o teu raciocínio.
3 cm
6 cm
Círculo Raio Diâmetro
A
B
C
261287 070-091.indd 76 30/05/14 17:53

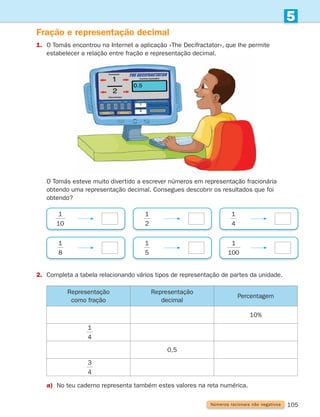
79. 77
4
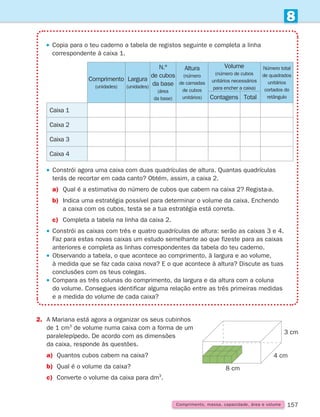
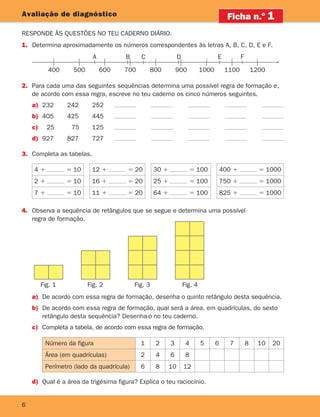
Figuras no plano e sólidos geométricos
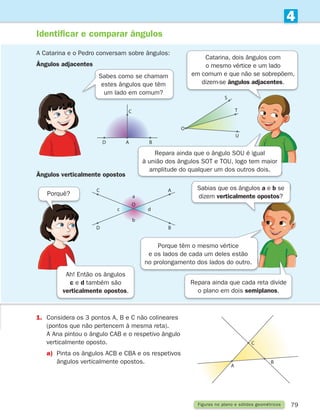
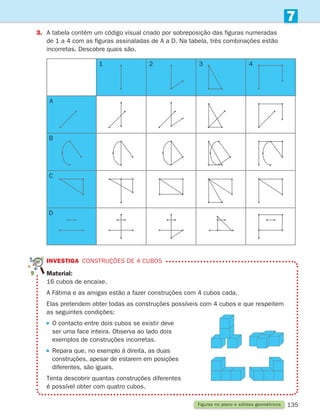
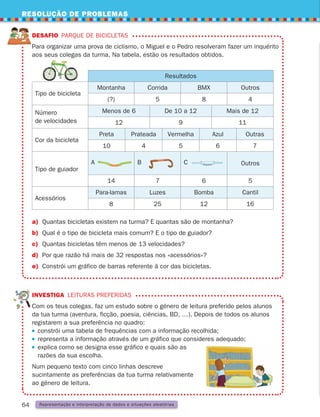
Noção de ângulo
Observa os ponteiros dos relógios.
Tomando como referência o centro do relógio, as direcções dos ponteiros formam um ângulo.
Quando são 2 horas, 3 horas e 4 horas, os ponteiros formam ângulos diferentes.
Um ângulo (convexo ou côncavo) é uma região limitada
por duas semirretas que têm a mesma origem.
As semirretas são os lados do ângulo, e a origem
dos lados é o vértice.
Não te esqueças!
Podemos observar dois tipos de ângulos.
Nas imagens estão assinalados a vermelho alguns ângulos. Identifica, na tua sala de aula,
ângulos nos objetos e diz se são ângulos convexos ou côncavos.
O ângulo convexo AOB é o conjunto de pontos pertencentes às semirretas
situadas entre O
?
A e O
?
B (semirretas com origem em O que intersetam
o segmento de reta [AB]).
O ângulo côncavo BOA é o complementar do ângulo convexo AOB unido
com as semirretas O
?
A e O
?
B.
Não te esqueças!
A
B
O
Ângulo convexo Ângulo côncavo
Lado
Lado
Vértice
A
B
O
261287 070-091.indd 77 30/05/14 17:53

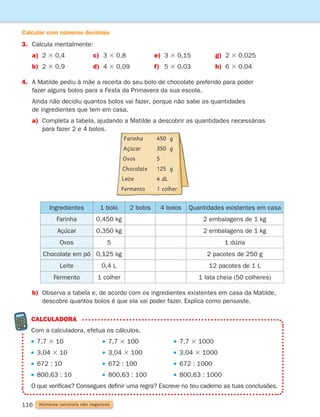
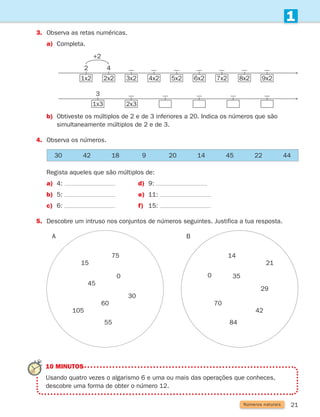
80. 78 Figuras no plano e sólidos geométricos
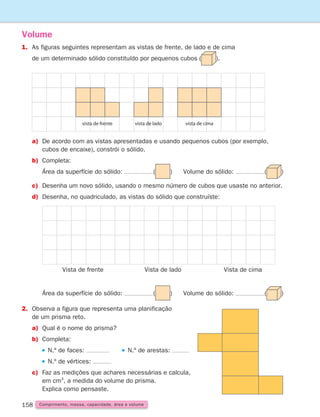
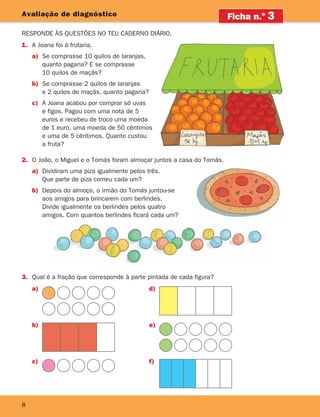
Amplitude de um ângulo
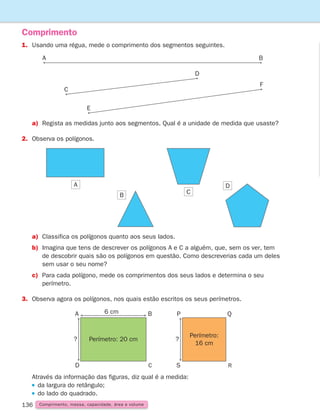
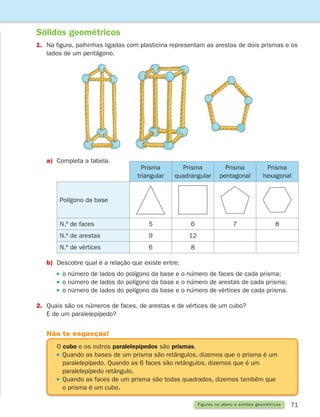
1. Usando papel vegetal copia o ângulo a e sobrepõe-no aos ângulos b, c, e d.
Descobre quais os que se podem sobrepor.
Diz-se que dois ângulos têm a mesma amplitude quando se podem sobrepor.
Quando dois ângulos têm a mesma amplitude dizem-se congruentes
ou geometricamente iguais.
Não te esqueças!
a
b
c
d
Outro modo de verificarmos se dois ângulos são geometricamente iguais é fixando pontos
nos seus lados e medindo distâncias.
Usando a régua, verifica que:
[BA] tem o mesmo comprimento que [ED]
[BC] tem o mesmo comprimento que [EF]
[AC] tem o mesmo comprimento que [DF]
Vais poder concluir que os ângulos a e b são iguais.
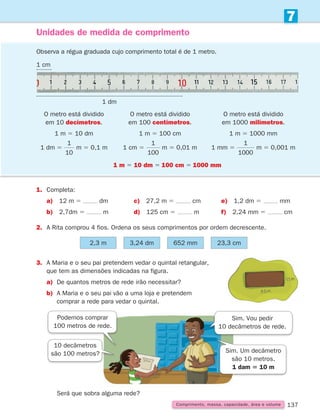
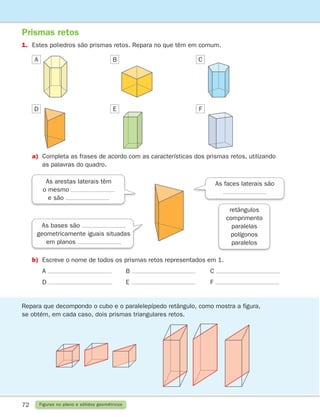
2.
Verifica se os seguintes pares de ângulos são iguais.
a) b)
b
a
B
a C
A
E
b F
D
b
a
261287 070-091.indd 78 30/05/14 17:53

81. 79
4
Figuras no plano e sólidos geométricos
1.
Considera os 3 pontos A, B e C não colineares
(pontos que não pertencem à mesma reta).
A Ana pintou o ângulo CAB e o respetivo ângulo
verticalmente oposto.
a)
Pinta os ângulos ACB e CBA e os respetivos
ângulos verticalmente opostos.
A
C
B
D
O
U
T
S
D B
C
a
b
O
c d
A
B
C
A
Identificar e comparar ângulos
A Catarina e o Pedro conversam sobre ângulos:
Ângulos adjacentes
Ângulos verticalmente opostos
Sabes como se chamam
estes ângulos que têm
um lado em comum?
Ah! Então os ângulos
c e d também são
verticalmente opostos.
Porquê?
Sabias que os ângulos a e b se
dizem verticalmente opostos?
Porque têm o mesmo vértice
e os lados de cada um deles estão
no prolongamento dos lados do outro.
Repara ainda que cada reta divide
o plano em dois semiplanos.
Repara ainda que o ângulo SOU é igual
à união dos ângulos SOT e TOU, logo tem maior
amplitude do qualquer um dos outros dois.
Catarina, dois ângulos com
o mesmo vértice e um lado
em comum e que não se sobrepõem,
dizem-se ângulos adjacentes.
261287 070-091.indd 79 30/05/14 17:53

82. 80 Figuras no plano e sólidos geométricos
1.
Constrói um medidor de ângulos.
Dobra um círculo em quatro partes iguais.
Desdobra e abre o papel. Deves ver, no centro, quatro ângulos retos. Cada um deles
tem uma amplitude de 90º. As dobras formam retas perpendiculares.
Volta a dobrar o círculo pelas mesmas marcas e depois dobra ao meio mais uma vez.
Desdobra o círculo e poderás observar oito ângulos, cada um com 45º.
2. Usa o teu medidor de ângulos.
a)
Descobre os ângulos que têm amplitude maior, menor ou igual a 90º e regista essas
observações no teu caderno.
b)
Decompõe os ângulos de amplitude maior do que 90º em dois ângulos adjacentes,
tendo um deles 90º.
A B C
D E
F
Os polígonos que têm os lados iguais e os ângulos iguais chamam-se polígonos regulares.
Não te esqueças!
Repara nos ângulos dos polígonos.
triângulo
equilátero
quadrado pentágono
regular
hexágono
regular
heptágono
regular
octógono
regular
Identificar e comparar ângulos
261287 070-091.indd 80 30/05/14 17:53

83. 81
4
Figuras no plano e sólidos geométricos
Descrição Amplitude Classificação Ângulo
Menos do que um
quarto de volta
Maior do que 0º
e menor do que 90º
Ângulo agudo
Um quarto de volta Igual a 90º Ângulo reto
Mais do que um
quarto de volta
Maior do que 90º
e menor do que 180º
Ângulo obtuso
Meia volta Igual a 180º Ângulo raso
Uma volta completa Igual a 360º Ângulo giro
Os lados do ângulo
coincidem
Igual a 0º Ângulo nulo
O
A
B
O
A
B
O
A
B
O
A B
O A B
O A B
c)
Classifica os ângulos da alínea a) com base na tabela.
3.
O transferidor é um instrumento que te permite medir a amplitude de um ângulo.
Observa.
a)
Completa as afirmações seguintes.
O ângulo com vértice em O e formado pelas semirretas OE O
e D
o o mede 60º.
É um ângulo
O ângulo com vértice em O e formado pelas semirretas e
OA OD
o o mede 120º.
É um ângulo
E A
B
C
D
O
261287 070-091.indd 81 30/05/14 17:53

84. 82 Figuras no plano e sólidos geométricos
Identificar e comparar ângulos
Com o transferidor, mede as amplitudes dos ângulos internos de cada quadrilátero
e compara os resultados com as tuas estimativas.
Para cada quadrilátero, calcula também a soma das amplitudes dos seus 4 ângulos
internos. Para apoiar o teu trabalho, podes completar a tabela seguinte.
Repara que dos quadriláteros anteriores apenas o retângulo tem os 4 ângulos retos.
INVESTIGA ângulos
Observa estes quadriláteros, estima as amplitudes
dos seus ângulos internos e assinala-as nas imagens.
O que podes concluir?
Nome do polígono
N.º de ângulos
internos
Amplitude
dos ângulos
Soma das amplitudes
dos ângulos internos
R 4 90º, 90º, 90º, 90º
T
L
P
a
d
b
c
e
g
f
h
i j
k
l
m n
o
p
L
P
T
R
261287 070-091.indd 82 30/05/14 17:53

85. 83
4
Figuras no plano e sólidos geométricos
1.
Analisa os seguintes triângulos.
A B C
D
a)
Completa:
Triângulo tem um ângulo reto Triângulo retângulo
Triângulos e todos os seus ângulos são agudos Triângulo acutângulo
Triângulo tem um ângulo obtuso Triângulo obtusângulo
b) Investiga o que acontece com a soma das amplitudes dos ângulos de um triângulo.
2.
Dois polígonos são geometricamente iguais se tiverem lados e ângulos iguais.
Verifica se os seguintes pares de polígonos são geometricamente iguais.
A B
D
C
261287 070-091.indd 83 30/05/14 17:53

86. 84 Figuras no plano e sólidos geométricos
Retas paralelas e retas concorrentes
Dobra uma folha quadrada, de modo a ficar dividida em quatro partes geometricamente
iguais, como mostra a figura. Podes dobrar ao meio e novamente ao meio. Observa os
vincos.
Dobra outra folha quadrada unindo lados ou unindo vértices, como mostram as figuras
seguintes. Observa os vincos.
Num plano, duas retas que não se intersetam
chamam-se paralelas.
Não te esqueças!
Num plano, duas retas concorrentes que formam ângulos retos são retas
perpendiculares.
Não te esqueças!
Num plano, duas retas que se intersetam num ponto chamam-se concorrentes.
Se se intersetam em dois pontos, então coincidem e dizem-se coincidentes.
Não te esqueças!
Retas paralelas Retas não paralelas
261287 070-091.indd 84 30/05/14 17:53

87. 85
1.
Observa os polígonos e classifica as afirmações como verdadeiras ou falsas.
4
Figuras no plano e sólidos geométricos
2.
Observa o mapa.
Na figura A, há dois pares de lados
paralelos.
Na figura C, o segmento de reta GE
é perpendicular a GH.
A figura D tem dois lados paralelos.
O triângulo tem um ângulo reto
e dois agudos.
A soma dos ângulos internos
do quadrado é 180º.
a) Refere duas ruas que sejam paralelas.
b)
Dá exemplos de ruas que sejam perpendiculares.
c)
A Avenida 24 e a Rua 20 são paralelas?
d)
A Rua 34, que não se vê no mapa, é paralela à Rua 26. Também será paralela
à Avenida 24?
e)
As Ruas 36 e 38 (não representadas na planta) são perpendiculares à Rua 33.
Podes dizer se são paralelas ou perpendiculares entre si?
f)
Baseando-te no mapa, formula questões para colocares aos teus colegas.
E F
H G
A
C
B
D
261287 070-091.indd 85 30/05/14 17:53

88. 86 Figuras no plano e sólidos geométricos
Simetrias de reflexão
Nas imagens, a linha azul divide as figuras em duas partes. Quando pões um espelho sobre
essa linha, a parte que fica em frente ao espelho, juntamente com o seu reflexo, «forma»
uma figura igual à inicial. Se dobrares a figura por essa linha, as duas partes da figura são
coincidentes.
1.
Pega numa folha quadrada e dobra-a ao meio. Desdobra-o e marca a linha de dobragem.
Essa linha é um eixo de simetria da figura.
a)
No quadrado, está marcado um eixo de simetria. Encontra todos os seus eixos
de simetria e desenha-os com cores diferentes.
Dizemos que a linha azul é um eixo de simetria, ou eixo de reflexão.
b) Investiga o número de eixos de simetria de outras figuras e regista as conclusões
na seguinte tabela.
c)
Marca eixos de simetria no círculo.
Figuras Número de lados Número de eixos de simetria
Quadrado 4
Triângulo equilátero
Pentágono regular
Hexágono regular
Retângulo
261287 070-091.indd 86 30/05/14 17:53

89. 87
4
Figuras no plano e sólidos geométricos
2.
Observa e responde às questões.
a)
Em que figura a linha verde é um eixo de simetria? Verifica a tua resposta com
um espelho ou mira.
b)
Encontra, nas figuras, eixos de simetria que não estejam assinalados.
3.
Os desenhos estão incompletos. Completa-os de modo que cada reta tracejada seja
um eixo de simetria da figura completa.
DESAFIO eixos de simetria
As figuras representam as faces de um dado.
Qual é o número de eixos de simetria de cada figura? Utiliza um espelho ou uma mira
para te ajudar.
A B C D E F
A B C D
A B
C D
261287 070-091.indd 87 30/05/14 17:53

90. 88
1. Vamos construir partes de frisos usando a figura seguinte.
Figuras no plano e sólidos geométricos
Frisos
a)
No friso 1, o motivo desloca-se para a direita. Desenha o 4.º elemento.
Friso 1
Friso 1
Friso 2
Friso 2
Friso 3
Friso 3
b)
No friso 2, o motivo reflete-se segundo um eixo vertical. Desenha o 3.º e o 4.º
elementos do friso. Podes utilizar um espelho ou uma mira.
c)
No friso 3, o motivo desloca-se para a direita e depois reflete-se segundo um eixo
horizontal. Desenha o 4.º elemento.
espelho espelho
261287 070-091.indd 88 30/05/14 17:53

91. 89
4
Figuras no plano e sólidos geométricos
d)
No friso 4, imaginando pontos fixos (X), rodamos meia volta o modelo. Desenha o
elemento seguinte.
Friso 4
Friso 4
2.
Experimenta construir frisos utilizando como motivo o trapézio.
a)
Constrói um friso usando reflexões sucessivas.
b)
Constrói um friso usando translações sucessivas.
c)
O que verificas acerca da posição das figuras nos dois frisos?
3.
Podes experimentar fazer um friso com a letra A. Recorre à:
a)
reflexão (usando um espelho ou mira);
b)
translação (deslocando a figura).
4.
Experimenta com a letra B. Achas que vai acontecer o mesmo que aconteceu com a letra A?
5. Investiga simetrias com outras letras ou palavras como, por exemplo, a palavra «ovo».
No friso 1, o motivo sofreu uma translação, deslocando-se 6 quadrículas
para a direita.
No friso 2, o motivo sofreu uma reflexão segundo um eixo vertical.
No friso 3, deslocámos o motivo 6 quadrículas para a direita (translação)
e em seguida fez-se uma reflexão segundo um eixo horizontal. Realizámos
uma reflexão deslizante.
No friso 4, rodámos o motivo meia volta (180º). Fizemos uma rotação de 180º.
Não te esqueças!
261287 070-091.indd 89 30/05/14 17:53

92. 90
1.
Pega num círculo (construído em papel) e dobra-o ao meio de modo que as duas partes
sejam congruentes.
Abre o círculo e, com um lápis de cor azul, marca a linha do vinco como mostra
a figura. Dobra-o de novo de modo a obteres outra linha e marca-a com a cor verde.
REVISÃO
a)
Assinala o centro do círculo.
b) Como se designam as linhas traçadas?
c)
Marca um raio a vermelho.
d)
Traça um segmento de reta que tenha por extremos dois pontos da circunferência
mas que não passe pelo centro. Ao segmento de reta traçado poderemos chamar
diâmetro?
2.
Observa as figuras e diz se as afirmações são verdadeiras ou falsas.
As figuras são polígonos.
O triângulo tem dois lados perpendiculares.
O paralelogramo só tem ângulos agudos.
O paralelogramo tem lados paralelos.
3.
Desenha, no teu caderno, um polígono que tenha apenas três ângulos internos: dois
ângulos agudos e um ângulo reto.
Qual é o nome da figura que desenhaste?
4. Marca os eixos de simetria na figura seguinte.
261287 070-091.indd 90 30/05/14 17:53

93. 91
4
5.
Observa a figura.
a)
A Avenida da Paz é
perpendicular à Rua
da Escola. Concordas?
Porquê?
b)
O Largo Verde tem
a forma de um polígono.
Indica o nome desse
polígono.
c)
A Rua do Parque, que
não se vê, é paralela
à Avenida da Paz. Qual é
a sua posição em relação
à Rua da Escola?
6.
Constrói, no teu caderno, uma figura que tenha:
a)
apenas um eixo de simetria;
b)
apenas dois eixos de simetria.
7.
Observa o friso e explica como pode ter sido obtido.
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
8. Identifica as figuras em que a linha azul é um eixo de reflexão.
A C
B D
261287 070-091.indd 91 30/05/14 17:53

94. 92
5
UNIDADE
A Mara e os colegas estão a jogar ao Jogo dos Racionais, em que cada
equipa tem de ordenar os seus cinco cartões com números racionais.
A equipa da Mara já terminou. Os seus estão bem ordenados?
261287 092-113.indd 92 30/05/14 17:54

95. 93
Números racionais não negativos
Frações em vários contextos
1.
Na segunda-feira, o Pedro e mais quatro amigos dividiram, em partes iguais, uma piza
ao almoço. Quanto coube a cada um?
2.
No dia seguinte, os cinco amigos decidiram comprar duas pizas para o almoço e dividi-las
em partes iguais. Que porção de piza coube a cada amigo?
3.
O Rodolfo dividiu um chocolate em quatro partes iguais e comeu duas dessas partes.
Que porção do chocolate comeu?
4.
Para o lanche na escola havia dois bolos do mesmo tamanho, um de chocolate e outro
de iogurte. O bolo de chocolate foi partilhado igualmente pela Inês, pela Ana e pelo Diogo;
o de iogurte foi partilhado igualmente pela Maria, pelo Tiago, pelo Rui e pela Joana.
a) Com que parte do seu bolo ficou cada uma das crianças?
b) Comeram todas a mesma quantidade de bolo? Explica como pensaste.
261287 092-113.indd 93 30/05/14 17:54

96. 94 Números racionais não negativos
5. Observa os círculos seguintes.
Carla Sara
A Carla poderá ter razão no que diz? Porquê?
DESAFIO Metades de chocolates
A Carla comeu metade de um chocolate e a Sara comeu metade de outro chocolate.
Lê os comentários das duas.
Não é verdade, comeste
exatamente a mesma
quantidade de chocolate
que eu.
Comi mais
chocolate
do que tu.
a) Escreve uma fração que represente a parte pintada em cada círculo.
b) Compara as frações que escreveste e ordena-as por ordem crescente.
6.
No domingo à tarde a Bruna e as três primas tinham cinco maçãs iguais para o lanche.
Todas gostam muito de maçã e decidiram reparti-las igualmente pelas quatro.
Que quantidade de maçã comeu cada uma?
a)
Depois de comerem as maçãs, decidiram repartir seis barrinhas de cereais iguais
pelas quatro. Que quantidade de barra de cereais comeu cada uma?
A B C D E
Frações em vários contextos
261287 092-113.indd 94 30/05/14 17:54

97. 95
5
Números racionais não negativos
7.
A Maria está a reciclar uma pulseira branca da mãe, pintando-a com novas cores.
DESAFIO Bolachas em partes
O Diogo colocou todas as bolachas
de um pacote sobre a mesa segundo
uma disposição retangular.
DESAFIO Frações equivalentes
Será que frações diferentes podem representar a mesma quantidade?
Indica uma fração que represente a parte pintada de cada desenho e discute com
os teus colegas a relação entre essas frações.
a)
Que parte da pulseira está pintada de vermelho?
b)
Que parte da pulseira está pintada de azul?
c)
Que parte da pulseira ainda está por pintar?
Consegues descobrir outros pares de frações que representam a mesma
quantidade?
Se comer
1
3
2
3
do pacote,
como 12 bolachas.
Quantas bolachas come o Diogo se comer
1
2
5
6
4
9
14
36
3
4
do total?
Quantas bolachas come o Diogo se comer
1
2
5
6
4
9
14
36
3
4
do total?
Quantas bolachas come o Diogo se comer
1
2
5
6
4
9
14
36
3
4
do total?
Quantas bolachas come ele se comer
1
2
5
6
4
9
14
36
3
4
do total?
Quantas bolachas come o Diogo se comer
1
2
5
6
4
9
14
36
3
4
do total?
261287 092-113.indd 95 30/05/14 17:54

98. 96 Números racionais não negativos
8.
A família do Bruno vai para a sua casa de férias,
que fica a uma distância de 240 km.
a)
À hora de almoço já fizeram
1
3
2
3
da viagem. Quantos quilómetros
já percorreram? Quanto falta ainda?
9.
Desenha no teu caderno 12 lápis.
a)
Pinta-os pela seguinte ordem e com
as cores indicadas:
de vermelho, metade dos lápis;
de azul, um terço dos lápis que
sobram;
de verde, metade dos lápis que
sobram;
de amarelo, os restantes lápis.
b)
Quantos lápis pintaste de cada cor?
DESAFIO o agricultor e o azeite
O Sr. Ricardo, no ano passado, obteve 600 litros de azeite. Sabemos que:
deu metade do azeite, em partes iguais, aos seus cinco filhos;
do restante, guardou dois terços para seu consumo próprio;
vendeu o azeite que sobrou, a 3,5 € cada litro.
a) Quantos litros de azeite deu a cada filho?
b) Quantos litros de azeite vendeu?
c) Quanto dinheiro apurou o agricultor com a venda do azeite?
b)
O Bruno decidiu levar
1
5
da sua
coleção de 30 DVD. Quantos DVD levou?
Frações em vários contextos
261287 092-113.indd 96 30/05/14 17:54

99. 97
5
Números racionais não negativos
Frações e percentagens
1.
Observa as figuras seguintes.
a) Representa em forma de fração a parte pintada de cada figura.
b)
Em quais das figuras anteriores a parte pintada é 25% do total? E em que é 50%?
E em que é 75%?
2. A imagem representa 25% de uma barra de chocolate.
a) Desenha no teu caderno 50% da barra de chocolate.
b) Desenha 75% da barra de chocolate.
A
E F G H I
B C D
3. No saco estão 30% dos berlindes do Paulo.
a) No teu caderno, desenha 100% dos seus berlindes.
b) Que percentagem representa um berlinde?
4. No teu caderno constrói 4 quadrados com 10 quadrículas de lado.
a)
Divide cada quadrado em partes iguais e pinta algumas dessas partes de modo que:
Quadrado 1 — a parte pintada corresponda a
1
4
do quadrado;
Quadrado 2 — a parte pintada corresponda a
3
4
do quadrado;
Quadrado 3 — a parte pintada corresponda a 10% do quadrado;
Quadrado 4 — a parte pintada corresponda a 0,3 do quadrado.
b) Qual é o quadrado que está 25% pintado? E qual está 75% pintado?
261287 092-113.indd 97 30/05/14 17:54

100. 98 Números racionais não negativos
Frações e medida de áreas
1.
Os blocos-padrão têm várias figuras:
Paralelogramos azuis
Trapézios vermelhos
Hexágonos amarelos
Triângulos verdes
Quadrados cor
de laranja
Paralelogramos
castanhos
Manipula e compara as várias figuras e responde, no teu caderno, às questões
sobre as áreas.
a) Se a área de medir
1
2
1
3
1
6
, qual é a figura cuja área mede 1?
b) Se a área de medir
1
2
1
3
1
6
, qual é a figura cuja área mede 1?
c) Se a área de medir
1
2
1
3
1
6
, qual é a figura cuja área mede 1?
d) Se a área de medir
1
2
1
3
1
6
, qual é a figura cuja área mede 1?
e) Se a área de medir
1
2
1
3
1
6
, qual é a figura cuja área mede 1?
f) Se a área de medir
1
2
1
3
1
6
, qual é a figura cuja área mede 3?
g) Se a soma das áreas das figuras e for 1, quanto mede
a área de ?
h) Se a soma das áreas das figuras e for 1, quanto é a soma
das áreas das figuras e ?
261287 092-113.indd 98 30/05/14 17:54

101. 99
5
Números racionais não negativos
Frações
1.
Completa:
a)
2:3
3
2
1
5 5 3 b) :
4
5
5
4
1
5 5 5 3
2.
Observa a piza, que está dividida em 8 fatias.
Verifica que
8
2
da piza é equivalente a
1
4
da piza.
a)
Desenha uma nova piza e divide-a
em 10 fatias. Verifica que
10
4
é equivalente
a
5
2
da piza.
3.
Determina uma fração equivalente a
20
12
com termos respetivamente menores.
4.
Completa as igualdades:
a)
8
2
4
=
1
8
4
=
20
12 3
=
5
10
6
=
b)
3
25
15
=
5
3
40
=
5
3 18
=
30 6
40
=
c)
100
230
10
=
12
100
120
=
3
50
30
=
240
130
24
=
Pretende-se dividir 2 chocolates por 4 crianças.
Observa as seguintes representações:
Repara que 2 : 4 5
1 1
4
1
4
1 5 1 5
2 4 4
2 3
5 2 3
1 1
4
1
4
1 5 1 5
2 4 4
2 3
.
1 1
4
1
4
1 5 1 5
2 4 4
2 3
é o quociente da divisão de 2 por 4, porque 4 3
1 1
4
1
4
1 5 1 5
2 4 4
2 3
5 2.
1 1
4
1
4
1 5 1 5
2 4 4
2 3
2 3
1 1
4
1
4
1 5 1 5
2 4 4
2 3
261287 092-113.indd 99 30/05/14 17:54

102. 100 Números racionais não negativos
Adicionar e subtrair frações
1.
Lê com atenção e resolve.
a)
A Matilde está a olhar para a tarte que sobrou do almoço. Que parte da tarte sobrou?
b)
Também sobrou parte da torta de chocolate. Que parte da torta sobrou?
0 1
2. Observa a reta numérica com a unidade dividida em cinco partes iguais.
Constrói geometricamente os resultados das seguintes operações e representa cada um
deles na forma de fração:
a)
5
6 2
5
6
5
2
1
5
- b)
5
6 2
5
6
5
2
1
5
-
3. Completa:
a)
1
5
1
5
1
5
1 1
2
1
2
1
1 1 1 5 1 5 1 1 5
1
3
1
5 6
2
6
2
2
3
1 5 b)
1
5
1
5
1
5
1 1
2
1
2
1
1 1 1 5 1 5 1 1 5
1
3
1
5 6
2
6
2
2
3
1 5 c)
1
5
1
5
1
5
1 1
2
1
2
1
1 1 1 5 1 5 1 1 5
1
3
1
5 6
2
6
2
2
3
1 5 d)
1
5
1
5
1
5
1 1
2
1
2
1
1 1 1 5 1 5 1 1 5
1
3
1
5 6
2
6
2
2
3
1 5
4. Escreve
5
3
1
3
como soma de parcelas todas iguais a
5
3
1
3
.
261287 092-113.indd 100 30/05/14 17:54

103. 101
5
Números racionais não negativos
5. Faz como a Daniela para calcular
a)
1 0
3
1 1 1
6
1
3
2
5
2
10
3
10
4
0
b)
1 0
3
1 1 1
6
1
3
2
5
2
10
3
10
4
0
c)
1 0
3
1 1 1
6
1
3
2
5
2
10
3
10
4
0
6. Responde:
a) O João comeu
5
1
de chocolate. Quanto sobrou?
b) Mais tarde, comeu mais
10
1
de chocolate.
Que parte do chocolate comeu no total?
7.
O irmão do Rafael está a cortar a relva do jardim.
Já cortou
8
3
da relva, que parte ainda falta?
Observa como é que a Daniela está a adicionar frações.
1 1
4
1
4
1 5 1 5
2 4 4
2 3
1 5 1 5
5
2
10
3
10
4
10
3
10
7
Como tenho um meio
e um quarto, vou ter de
passar tudo para quartos
para poder adicionar.
Agora, como quero adicionar 1 5 1
5
2
10
3
10
4
1
3
com
1 5 1 5
5
2
10
3
10
4
10
3
10
7
, tenho de encontrar
uma fração equivalente a 1 5 1 5
5
2
10
3
10
4
10
3
que
tenha denominador 10.
261287 092-113.indd 101 30/05/14 17:54

104. 102 Números racionais não negativos
Multiplicar e dividir frações
1.
A Sara dividiu um chocolate em barrinhas, como se mostra na figura. Completa as frases.
Cada barrinha é
20
do chocolate.
Se a Sara comer três barrinhas,
vai comer
20
do chocolate.
Se a Sara comer meia barrinha,
vai comer
20
do chocolate.
2.
A D. Cristina gastou numa semana
7
2
de uma embalagem de detergente.
Se continuar a gastar a mesma quantidade por semana, quanto
gastará em três semanas?
3. Completa:
a)
1
1 1 5
3
2 2
1
2
1
2
1
2
3 5 d)
5
2
1 1 1 5
4
5
2
5
2
5
2
5
2
3 5
b)
3
1
3
1
1 5
2
3
1
3 5 e)
5
4
1
3 5
c)
3
1
2 2
3
1
3 5 3 5 f)
5
2
3 3
5
2
3 5 3 5
4. Completa:
a)
2
3
4
3
2 4
3
3 5
3
5 c)
3
5
2
5
2
3 5
3
5
b)
3
2
5
3
2 5
3
3 5
3
5 d)
4
1
6
4
3 5
3
5
5. Completa:
a)
1
3 5 3 5 3 5
3
3
1
5
5
6
6
2
10
10
3
3 5 b)
1
3 5 3 5 3 5
3
3
1
5
5
6
6
2
10
10
3
3 5 c)
1
3 5 3 5 3 5
3
3
1
5
5
6
6
2
10
10
3
3 5 d)
1
3 5 3 5 3 5
3
3
1
5
5
6
6
2
10
10
3
3 5
261287 092-113.indd 102 30/05/14 17:54

105. 103
5
Números racionais não negativos
0 1
0 1
6.
A mãe do Diogo comprou uma piza que vinha
dividida em quartos. Antes de a colocar na mesa,
dividiu cada quarto de piza em 3 fatias.
Cada nova fatia que parte é da piza?
1
: 5
4
3
7.
Observa o segmento dividido em terços.
a) Divide um segmento de comprimento
1
3
em dois segmentos iguais.
De quantos destes novos segmentos precisas para preencher o segmento
unidade?
Qual é a medida de comprimento de cada um?
b) Completa a igualdade:
1 1
?
?
: 5
3
5
3
2
3 2
8.
Observa o segmento dividido em quartos.
a) Divide um segmento de comprimento
1
4
em três segmentos iguais.
De quantos destes novos segmentos precisas para preencher o segmento
unidade?
Qual é a medida de comprimento de cada um?
b) Completa a igualdade:
4
1
3
4
1
: 5
3
5
9.
Completa:
a) :
5
1
2= b) :
3
1
4= c) :
10
1
2= d) :
10
1
4=
261287 092-113.indd 103 30/05/14 17:54

106. 104 Números racionais não negativos
Números decimais
1.
Regista qual é o comprimento, em centímetros, de cada um destes objetos.
4. O Rodrigo está a preencher um jogo de palavras-cruzadas.
Responde a cada pergunta, escrevendo cada número de dois modos, como fração
e em representação decimal.
a)
Que parte representa a área de cada linha
relativamente à área total do jogo?
b)
Que parte representa a área de cada
quadrícula?
c)
Que parte do jogo é ocupada pela palavra
«MATEMÁTICA»?
d)
Que parte do jogo é ocupada pela palavra
«TRIÂNGULO»?
e)
Que parte do jogo está já preenchida com
letras?
f)
Que parte do jogo está pintada de cor
de laranja?
g)
Depois de preenchido todo o jogo, que parte vai ficar com letras?
M A T E M A T I C
T R A N G U L O
A
R
A
P
E
Z
I
O
A C I O N A L
1
1 2 3 4 5 6 7 9
8 10
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6
2.
Se um quadrado representa uma unidade, quais são os números representados pela
parte pintada?
3. Constrói no teu caderno uma reta numérica igual à seguinte e posiciona nela os números.
a) b) c)
0,4 1,3 3,4 4,5
2,7 5,6
261287 092-113.indd 104 30/05/14 17:54

107. 105
5
Números racionais não negativos
Fração e representação decimal
1.
O Tomás encontrou na Internet a aplicação «The Decifractator», que lhe permite
estabelecer a relação entre fração e representação decimal.
O Tomás esteve muito divertido a escrever números em representação fracionária
obtendo uma representação decimal. Consegues descobrir os resultados que foi
obtendo?
2.
Completa a tabela relacionando vários tipos de representação de partes da unidade.
a) No teu caderno representa também estes valores na reta numérica.
Representação
como fração
Representação
decimal
Percentagem
10%
0,5
1
4
3
4
1
10
1
2
1
4
1
8
1
5
1
100
261287 092-113.indd 105 30/05/14 17:55

108. investiga frações decimais
Fração e representação decimal
106 Números racionais não negativos
investiga fração e representação decimal
Procura na Internet o «The Decifractator» (escreve no motor de busca
«The Decifractator») e faz como o Tomás, escolhendo os teus próprios números.
Será que consegues transformar numa fração um número que esteja escrito
na representação decimal?
Experimenta, discute com os teus colegas e regista as tuas conclusões.
Oh, que giro. São precisamente essas
frações que eu uso quando quero
transformar numa fração um número
escrito na representação decimal.
3.
Após alguns minutos, o Tomás decidiu utilizar a aplicação «The Decifractator» de um
modo diferente. Pensava num número em representação decimal e tentava descobrir
uma fração que o representasse. Queres tentar?
0,4 0,3 0,7
0,25 0,32 0,234
?
?
?
?
?
?
?
?
?
?
?
?
As frações que têm como
denominador 10, 100,
1000, … chamam-se
frações decimais.
261287 092-113.indd 106 30/05/14 17:55

109. 107
5
Números racionais não negativos
Ordenar números racionais
Jogo Jogo dos racionais
Preparem 30 cartões e, com a ajuda do professor, escrevam um número racional
em cada cartão (frações, números inteiros e números decimais).
Organizem equipas de cinco elementos (são necessárias pelo menos duas equipas)
e escolham um árbitro.
Regras do jogo:
Cada equipa tira 5 cartões sem ver os números.
Quando o árbitro der sinal, cada equipa distribui um cartão por cada elemento
e depois devem alinhar-se de acordo com a ordem dos cartões.
Ganha a equipa que estiver mais rapidamente alinhada.
Também podes jogar o jogo sentado à mesa com o teu parceiro, sendo que, assim,
cada um de vocês tem de ordenar os seus cinco cartões.
Durante o Jogo dos Racionais, o Rafael sentiu algumas dificuldades. Observa a sua
conversa com a Mara.
1. E tu, já percebeste? Ordena cada um dos seguintes conjuntos de cartões.
a) b)
O meu cartão tem
o número 5…
E qual é maior?
O meu ou o teu?
Lê-se cinco unidades e três
décimas. O meu lê-se três
unidades e quarenta e cinco
centésimas.
Começas por comparar a parte
inteira. O teu número é maior
porque tem mais unidades.
Exatamente: o Luís tem o
cartão com o número 5,7. Tem
as mesmas unidades, por isso
tens de comparar as décimas.
Já percebi. Como
o número do Luís
tem sete décimas, ele
tem um número maior
do que o meu.
5,15 3,4 4,5
0,7 3,2
3,25 4,05 3,28
4,5 3,7
261287 092-113.indd 107 30/05/14 17:55

110. 108 Números racionais não negativos
A milésima
Observa a conversa entre o Ricardo e a Cláudia.
Aquilo que a Cláudia está a dizer corresponde a uma decomposição do número do seguinte
modo:
3,275 5 3 1 0,2 1 0,07 1 0,005
Sim! Nasceu com
três quilos, duzentos
e setenta e cinco
gramas.
Hum… Também podes dizer que nasceu
com três quilos e duas décimas, sete
centésimas e cinco milésimas de quilo.
O teu mano já nasceu?
Decomposição U d c m Leitura
4,067 5 4 1 0,06 1 0,007 4 0 6 7
Quatro unidades, seis centésimas
e sete milésimas
3,432 5 1 1 1
5 1 1 1 5 3 1 1
5 1 1 1
Sete unidades, seis décimas, quatro
centésimas e três milésimas
5 3 1 0,1 1 0,02 1 0,005
5 9 1 0,4 1 0,007
10 MINUTOS
Qual é o valor do 5 em cada caso?
a) 35,43 b) 567,46 c) 12,59 d) 342,05 e) 250,32 f) 123,345
1.
Completa a tabela seguinte.
261287 092-113.indd 108 30/05/14 17:55

111. 109
5
Números racionais não negativos
2. Escreve por ordem crescente.
3,3 0,3 3,03 0,003 0,03 3,303 3,033
3.
De entre os números maiores do que 3,4 e menores do que 3,5 que estão neste
conjunto, escolhe o que tem maior algarismo das centésimas e escreve-o no teu
caderno.
CALCULADORa
Que número deves adicionar a 2,346 para obteres:
a) 2,349 b) 2,446 c) 2,358 d) 3,349 e) 4,447 f) 8,888
Que número deves subtrair a 6,798 para obteres:
a) 6,790 b) 6,700 c) 4,700 d) 3,790 e) 6,708 f) 6,688
6. Continua estas sequências de números, de acordo com a regra.
1 0,005
1 0,025
1 0,005
1 0,025
…
…
1,001
1,001
1,006
1,026
5. Refere:
a) um número entre 4,1 e 4,2;
b) dois números entre 3,25 e 3,26;
c) três números entre 8,75 e 9,75.
4.
De entre os números maiores do que 7,75 e menores do que 7,76 que estão neste
conjunto, escolhe o que tem o algarismo das milésimas igual ao das décimas
e escreve-o no teu caderno.
3,45
3,48
3,51
3,59
7,747
7,758
7,751
7,757
261287 092-113.indd 109 30/05/14 17:55

112. 110 Números racionais não negativos
Estimar e calcular com números decimais
1.
Observa a tabela de preços de uma esplanada.
4. Calcula mentalmente trocando e agrupando as parcelas da forma que for mais fácil.
a) 12,4 1 4 1 3,6 c) 23, 2 1 3,5 1 4,8 1 3,5
b) 43,1 1 2,5 1 3,9 d) 3,45 1 2,3 1 3,55
5. Escreve os números escondidos.
a) 3,4 1 5 4,6 c) 2 2,5 5 5 e) 1 0,25 5 3,75
b) 1 2,6 5 8,9 d) 4,1 2 5 3,5 f) 4,5 2 5 2,25
6.
Completa os quadrados mágicos seguintes. A soma obtida em cada linha, em cada
coluna e nas diagonais tem de ser a mesma.
1,5 1 0,5
1,25 1 1,75
2,4 1 1,6
2,65 1 0,25
3,9 1 1,1
3,9 2 1,1
3,3 1 2,2
7,25 2 2,15
0,2 0,9
0,5
0,1
1,2
1
0,4 0,8
Se comeres uma sanduíche e uma bebida, qual é o lanche mais caro? Qual é o lanche
mais barato? Justifica a tua resposta.
2.
Se comprares 4 cadernos a 1,99 € cada, quanto vais pagar? E se comprares 5 canetas
a 0,49 € cada uma?
3. Calcula mentalmente:
Sanduíche de manteiga 0,80 €
Sanduíche de fiambre 1,25 €
Sanduíche mista 1,50 €
Sumo 1,05 €
Água 0,75 €
261287 092-113.indd 110 30/05/14 17:55

113. 111
5
Números racionais não negativos
7.
A Ana vai comprar pão à padaria.
a)
Se só tiver uma moeda
de 0,50 €, pode comprar
5 pães brancos?
b)
Se só tiver uma moeda de 1 €,
pode comprar 6 pães integrais?
c)
Com uma nota de 5 €, quantos
pães com chouriço pode
comprar?
8.
O Tiago também vai à padaria. Tem no bolso moedas de 0,20 €, 0,10 €, 0,05 €
e 0,02 €.
a)
De quantas formas diferentes pode pagar um pão branco sem receber troco? Regista
todas as hipóteses no teu caderno.
b)
Como pode pagar se decidir comprar 2 pães brancos? Regista todas as formas
de pagamento possíveis sem receber troco.
9.
Ajuda a mãe do Miguel a poupar algum dinheiro nas compras do supermercado.
O que fica mais económico?
a)
Quatro bolos de 50 g a 0,90 € cada um
ou um bolo de 200 g a 3,5 €?
b)
Duas embalagens de 125 g de manteiga
a 0,85 € cada uma ou uma embalagem
de 250 g a 1,45 €?
c) Uma embalagem de 250 mL
de champô a 2,49 € ou uma
embalagem de 400 mL a 4,35 €?
d)
Um conjunto de 4 garrafas de água
de 1,5 L a 1,15 € ou um garrafão
de 5 L a 0,99 €?
Padaria
Pão caseiro 1,25 €
Pão branco 0,12 €
Pão integral 0,15 €
Pão de água 0,20 €
Pão com chouriço 1,50 €
261287 092-113.indd 111 30/05/14 17:55

114. 112
REVISÃO
1.
A Bruna recebeu no Natal uma caixa de bombons. Observa a figura.
a)
Ela e a família comeram alguns. Que parte do total comeram?
Que parte falta comer?
3.
Quais são os números da reta numérica que correspondem às letras?
4.
Para cada uma das seguintes sequências, determina uma possível regra de formação e,
de acordo com essa regra, escreve os 3 números seguintes.
a)
0 0,7 1,4 2,1 2,8 3,5
b)
0,6 1,3 2,0 2,7 3,4 4,1
c)
5 6,2 7,4 8,6 9,8 11
A B C D E F
0 3
2
1
2.
Quatro amigos estão a dividir em partes iguais três pizas do mesmo tamanho
ao almoço. Que parte de piza come cada amigo?
b)
Quando chegou à escola, a Bruna verificou
que a sua amiga Rita também tinha
recebido uma caixa de chocolates igual.
Que parte é que a Rita já tinha comido?
Que parte é que ainda lhe faltava comer?
c)
O irmão da Bruna recebeu uma caixa de bombons diferente, com 18 bombons.
Se ele comer um terço, quantos bombons come? Quantos sobram?
261287 092-113.indd 112 30/05/14 17:55

115. 113
5
5.
Observa o tangram e relaciona duas a duas
as áreas das diferentes peças do jogo.
«Um triângulo grande tem área igual
à de quatro triângulos pequenos.»
«Um triângulo pequeno tem
1
4
da área
de um triângulo grande.»
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
1,2 0,2 0,3 0,7 0,7
1,2
2,5
5,5
6.
Completa estas pirâmides de números, sabendo que cada número é a soma dos dois
que estão por baixo.
a) Completa a tabela.
Unidade de medida
Triângulo
pequeno
Triângulo
médio
Triângulo
grande
Área total
do jogo
Peça
Triângulo grande 4
Triângulo médio
Quadrado
Paralelogramo
Triângulo pequeno
1
4
1
4
261287 092-113.indd 113 30/05/14 17:55

116. 114
6
UNIDADE
Enquanto o pai abastece o carro, o Francisco e o irmão estão a olhar
para os preços dos combustíveis.
Qual é o combustível mais caro? E o mais barato?
261287 114-131.indd 114 30/05/14 17:56

117. 115
Calcular com números decimais
Números racionais não negativos
a) Explica por palavras tuas a estratégia usada pelo Rodrigo.
b) Se cada um dos quatro ratinhos comesse 0,25 do queijo, quanto comeriam no total?
a) Quanto pagou cada uma das amigas pelo seu almoço?
b)
Se a Joana almoçar todos os dias o mesmo, quanto gasta numa semana
(de segunda a sexta)?
2. O João e o Rodrigo estão a tentar resolver o seguinte problema:
«Quatro ratinhos comeram 0,15 de 1 queijo cada um. Quanto comeram no total?»
Calculadora
Observa o desenho da página ao lado e, com a ajuda da calculadora, responde
às questões.
a) O rapaz da moto abasteceu apenas 10 L de gasolina 95. Quanto pagou?
b) O camionista abasteceu 100 L de gasóleo. Quanto pagou?
c) O Sr. Gonçalves pagou 50 € de gasolina 98. Quantos litros comprou?
d)
Se no dia seguinte todos os combustíveis sofressem um aumento de 0,05 €,
por litro, quais seriam os novos preços?
1. A Rita, a Joana e a Catarina foram almoçar juntas.
Eu calculei
mentalmente:
4 3 0,15
Pensei em 4 3 15
centésimas, dá 60
centésimas.
Ou seja, 0,60.
Eu calculei: 0,15
0,15
0,15
1 0,15
0,60
Rodrigo
João
Rita
Prato 6,60 €
Sumo 1,25 €
Doce 1,75 €
Joana
Prato 6,60 €
Água 0,50 €
Gelado 1,40 €
Catarina
Prato 6,60 €
Sumo 1,05 €
Fruta 1,55 €
261287 114-131.indd 115 30/05/14 17:56

118. 116 Números racionais não negativos
3. Calcula mentalmente:
a)
2 3 0,4 c)
3 3 0,8 e)
3 3 0,15 g)
2 3 0,025
b)
2 3 0,9 d)
4 3 0,09 f)
5 3 0,03 h)
6 3 0,04
4.
A Matilde pediu à mãe a receita do seu bolo de chocolate preferido para poder
fazer alguns bolos para a Festa da Primavera da sua escola.
Ainda não decidiu quantos bolos vai fazer, porque não sabe as quantidades
de ingredientes que tem em casa.
a)
Completa a tabela, ajudando a Matilde a descobrir as quantidades necessárias
para fazer 2 e 4 bolos.
Ingredientes 1 bolo 2 bolos 4 bolos Quantidades existentes em casa
Farinha 0,450 kg 2 embalagens de 1 kg
Açúcar 0,350 kg 2 embalagens de 1 kg
Ovos 5 1 dúzia
Chocolate em pó 0,125 kg 2 pacotes de 250 g
Leite 0,4 L 12 pacotes de 1 L
Fermento 1 colher 1 lata cheia (50 colheres)
b)
Observa a tabela e, de acordo com os ingredientes existentes em casa da Matilde,
descobre quantos bolos é que ela vai poder fazer. Explica como pensaste.
calculadora
Com a calculadora, efetua os cálculos.
7,7 3 10 7,7 3 100 7,7 3 1000
3,04 3 10 3,04 3 100 3,04 3 1000
672 : 10 672 : 100 672 : 1000
800,63 : 10 800,63 : 100 800,63 : 1000
O que verificas? Consegues definir uma regra? Escreve no teu caderno as tuas conclusões.
Farinha 450 g
Açúcar 350 g
Ovos 5
Chocolate 125 g
Leite 4 dL
Fermento 1 colher
Calcular com números decimais
261287 114-131.indd 116 30/05/14 17:56

119. 117
6
1. Completa:
Multiplicar por 0,1, por 0,01 e por 0,001
3 ?
3100 :10
30,1 30,01
3100
25 ?
30,1 :10
3100 310
30,01
2.
O Miguel já gastou um décimo da sua mesada de 25 €. Quanto dinheiro é que ainda tem?
Números racionais não negativos
3 3 0,1
17 3 0,1
374 3 0,1
4,5 3 0,1
3 : 10
17 : 10
374 : 10
4,5 : 10
3 3 0,01
17 3 0,01
374 3 0,01
4,5 3 0,01
3 : 100
17 : 100
374 : 100
4,5 : 100
3 3 0,001
17 3 0,001
374 3 0,001
4,5 3 0,001
3 : 1000
17 : 1000
374 : 1000
4,5 : 1000
investiga
Com a calculadora efetua os cálculos.
a)
O que verificas? Consegues definir uma regra?
Escreve no teu caderno as tuas conclusões.
b)
O que verificas? Consegues definir uma regra?
Escreve no teu caderno as tuas conclusões.
c)
O que verificas? Consegues definir uma regra?
Escreve no teu caderno as tuas conclusões.
132 ?
30,1 :10
3100 310
30,01
0,15 ?
3100 30,01
:10 30,1
31000
261287 114-131.indd 117 30/05/14 17:56

120. 118
Multiplicar e estimar com números decimais
1. Copia a tabela para o teu caderno e completa-a.
3 0,1 0,2 0,01 0,02 0,001
125
2500
45
2. Na sua retrosaria, o Sr. Manuel está a conferir as vendas do dia.
a)
Vendeu 0,25 de um rolo de fio azul que media
140 m. Que quantidade de fio azul vendeu?
b)
Vendeu 0,1 de um rolo de fio vermelho que media
245 m. Que quantidade de fio vermelho vendeu?
c)
Vendeu 50 m de um rolo de fio verde que media
150 m. Que fração do rolo de fio verde vendeu?
3.
A Margarida comprou 5 cadernos a 3,99 € cada. Quanto dinheiro gastou?
4. Calcula mentalmente:
a) o preço de 4 chocolates que custam 0,95 € cada;
b) o preço de 2,5 kg de maçãs que custam 0,80 € o quilo;
c) o preço de 0,75 m de um tecido que custa 6 € o metro;
d) o número de garrafas de 1,5 L necessário para encher um depósito de 6 litros.
5.
O Miguel levou um pacote de bolachas para o recreio.
Ficou com metade das bolachas para si, deu
1
4
das
bolachas ao Afonso e deu as restantes ao Diogo.
a) Que parte das bolachas comeu o Diogo?
b)
Sabendo que o pacote tinha 20 bolachas, quantas
bolachas comeu cada um dos amigos?
6. Em cada caso, qual está mais perto de 10?
a) 0,1 3 1005 , 0,1 3 12 ou 0,1 3 108 ?
b) 0,1 3 105 , 107 : 10 ou 0,1 3 102 ?
c) 0,1 3 105 , 1 : 0,1 ou 0,01 3 1002 ?
Números racionais não negativos
261287 114-131.indd 118 30/05/14 17:56

121. 119
6
7. A Leonor saiu de casa com os 35 euros que recebeu pelo seu aniversário.
Fatores
Números inteiros
mais próximos
Estimativa Produto exato
4,12 3 7,9 4 3 8 32 32,548
0,9 3 43,2
8,04 3 5,8 8 3 6
454,3 3 10,1
34,2 3 19,8 680
6,234 3 2,987
Números racionais não negativos
10 MINUTOS
Em cada conjunto identifica o maior número e circunda-o.
1,7
0,995 1,625
1,288
2,345
2,302 1,9
2,73
a)
Gastou 20% do seu dinheiro num livro. Quanto custou o livro?
b)
Depois de comprar o livro, viu numa montra uma saia que estava em promoção com
um desconto de 30%. Sabendo que a saia tinha um preço inicial de 40 €, qual era
o novo preço da saia? A Leonor ainda tinha dinheiro suficiente para a comprar?
8.
Observa a tabela e faz uma estimativa de cada produto arredondando aos números
inteiros mais próximos dos fatores. Depois, com a calculadora, efetua
a operação e regista o produto exato.
A B
261287 114-131.indd 119 30/05/14 17:56

122. 120
Algoritmo da multiplicação com números decimais
A Mafalda, o Diogo, a Lara e o Afonso comeram 4 fatias de um bolo que estava dividido em
dez fatias iguais. O bolo inteiro pesava 872 g e os amigos estão curiosos por saber quanto
pesavam as suas quatro fatias.
Os amigos ficaram surpreendidos com a ideia da Mafalda, porque nunca tinham usado
o algoritmo para multiplicar números decimais. Ela explicou como fazer.
1.
Percebeste como fez a Mafalda? No teu caderno, efetua as seguintes operações usando
o algoritmo explicado pela Mafalda.
a) 45 3 1,2
b) 2,5 3 3,7
É muito fácil. Em primeiro
lugar, efetuamos a operação,
como já sabemos fazer.
Depois, temos de colocar
no produto a vírgula de modo
que o número de casas decimais
seja a soma dos números
de casas decimais dos fatores.
Neste caso, é só uma.
Números racionais não negativos
Como cada fatia é uma
décima do bolo, temos de
saber quanto é 0,4 de 872 g.
Isso é fácil. Uma décima
pesa 87,2 g. Só temos
de calcular 4 3 87,2.
Ou, então, podemos
usar o algoritmo
para calcular quanto
é 0,4 3 872.
8 7 2
30,4
3 4 8, 8
261287 114-131.indd 120 30/05/14 17:56

123. 121
6
2.
Um hipermercado está a fazer promoção de embalagens de 0,33 L de sumo de laranja.
a) Quantos litros de sumo há em cada conjunto de 24 garrafas?
b) Se cada garrafa custa 1,25 €, qual é o preço da embalagem inteira?
c)
Considerando a promoção «Se levar uma embalagem inteira só paga 0,8 do seu
preço», quanto se paga por uma embalagem inteira?
3. A família do Miguel consome 1,2 L de leite por dia.
a)
Quantos litros consome durante o mês de março?
b)
Se cada litro custa 0,60 €, quanto gasta para comprar
o leite necessário para o mês de março?
Números racionais não negativos
4.
A mãe da Catarina foi às compras à frutaria perto de sua casa.
a)
Comprou 2,5 kg de laranjas a 1,20 €/kg e 1,5 kg de maçãs a 0,80 €/kg. Quanto
gastou em fruta?
b)
Comprou também 5 kg de batatas a 0,65 €/kg e 0,5 kg de cebolas a 0,70 €/kg.
Quanto gastou no total?
DESAFIO a pintura do quarto
O Fernando pediu ao pai para pintar de azul uma das paredes do seu quarto.
Efetuou medições para saber que quantidade de tinta tinha de comprar.
a) A parede tem 3,5 m de largura por 3 m de altura. Qual é a área total a pintar?
b)
Para as várias demãos são necessários 0,2 L de tinta por cada metro quadrado.
Que quantidade de tinta é necessário comprar?
c)
No supermercado havia dois tipos de tinta azul.
Observa a figura e ajuda o Fernando a escolher
a opção mais económica.
Explica como pensaste.
261287 114-131.indd 121 30/05/14 17:56

124. 122
Divisão com números decimais
1.
Uma formiga percorreu 9,6 metros em 3 minutos sempre à mesma velocidade.
Que distância percorreu em cada minuto?
2.
Um caracol percorreu 0,36 metros em 3 minutos sempre à mesma velocidade.
Que distância percorreu em cada minuto?
3.
O Bruno tem um mealheiro cheio de moedas de 0,50 € e quer ir comprar um boné que
custa 2,5 €. De quantas moedas vai precisar?
4.
A Maria quer encher a máquina de água, que está vazia e tem um depósito de 2 L, mas
só tem garrafas de 0,25 L. De quantas garrafas vai precisar?
Números racionais não negativos
10 MINUTOS
Calcula mentalmente:
a) 0,4 : 4 c) 0,4 : 2 e) 0,06 : 6 g) 0,24 : 2
b) 7,5 : 3 d) 2,5 : 5 f) 4,8 : 4 h) 3,6 : 3
261287 114-131.indd 122 30/05/14 17:56

125. 123
6
1.
A Maria preparou 2 L de gelatina de morango
que quer distribuir por tacinhas. Cada taça
leva 0,1 L. De quantas taças vai precisar?
Dividir por 0,1, por 0,01 e por 0,001
2.
O Tomás está a alinhar lápis de cera
em cima da mesa da sala a toda
a sua largura. A mesa mede 1,2 m
de largura e os lápis medem 0,1 m.
Quantos lápis vai conseguir alinhar?
Números racionais não negativos
3 : 0,1
17 : 0,1
374 : 0,1
4,5 : 0,1
3 3 10
17 3 10
374 3 10
4,5 3 10
3 : 0,01
17 : 0,01
374 : 0,01
4,5 : 0,01
3 3 100
17 3 100
374 3 100
4,5 3 100
3 : 0,001
17 : 0,001
374 : 0,001
4,5 : 0,001
3 3 1000
17 3 1000
374 3 1000
4,5 3 1000
investiga
Com a calculadora, efetua os cálculos seguintes.
a)
O que verificas? Consegues
definir uma regra?
Escreve no teu caderno
as tuas conclusões.
b) Efetua agora:
O que verificas? Consegues
definir uma regra?
Escreve no teu caderno
as tuas conclusões.
c) Efetua agora:
O que verificas? Consegues
definir uma regra?
Escreve no teu caderno
as tuas conclusões.
261287 114-131.indd 123 30/05/14 17:56

126. 124
Algoritmo da divisão com números decimais
A Joana está a ajudar o avô a calcular quantas garrafas tem de comprar para engarrafar
o azeite produzido este ano.
Repara no modo como a Joana usou o algoritmo.
4 6 5
2 3 7 5
9 0
2 7 5
1 5
2 1 5
0
0,7 5
5 0 0
1 0 0
2 0
6 2 0
10 3 0,75 5 7,5 (¢Ë $poucø)
100 3 0,75 5 75 (¢Ë $poucø)
1000 3 0,75 5 750 (¢Ë muitø)
500 3 0,75 5 375
20 3 0,75 5 15
Calculou os múltiplos
de 0,75 necessários
para efetuar a divisão.
1.
O avô da Joana tem ainda 48 L de um azeite de casta especial que quer engarrafar
em garrafas de 0,40 L. Consegues também usar o algoritmo da divisão para saber
quantas garrafas destas é que ele vai necessitar de comprar?
Números racionais não negativos
Joana, tenho aqui 75 L de azeite
suave que quero engarrafar em
garrafas de 0,5 L. Quantas garrafas
destas tenho de comprar?
Vou querer engarrafar
os 465 L de azeite normal
em garrafas de 0,75 L.
De quantas garrafas
de 0,75 L preciso?
Esse cálculo é difícil. Não tenho calculadora,
mas vou usar o algoritmo da divisão.
Tenho de dividir 465 por 0,75…
Precisas de 620 garrafas de 0,75 L.
Avô, eu consigo
calcular mentalmente:
2 garrafas dão para
1 L, por isso,
150 garrafas vão dar
para os 75 L.
261287 114-131.indd 124 30/05/14 17:56

127. 125
6
A Mariana comprou 2,5 metros de fio de pesca para fazer pulseiras de missangas.
Para cada pulseira necessita de 0,22 metros de fio. Quantas pulseiras pode fazer?
Repara no modo como a Mariana usou o algoritmo da divisão para descobrir quantas
pulseiras ia poder fazer.
2. Calcula mentalmente em cadeia e escreve os resultados das operações.
10 3 3,2 5 10 3 1,7 5 10 3 0,72 5
100 3 3,2 5 100 3 1,7 5 20 3 0,72 5
50 3 3,2 5 1000 3 1,7 5 40 3 0,72 5
20 3 3,2 5 500 3 1,7 5 100 3 0,72 5
3. No teu caderno, efetua as operações seguintes.
a) 13 : 0,6 b) 3,5 : 0,2
A Mariana teve o cuidado
de colocar o dividendo
e o divisor com o mesmo
número de casas decimais.
2,5 0
2 2,2 0
0,3 0
2 0,2 2
0,0 8
0,2 2
1 0
1
1 1
10 3 0,22 5 2,20
Números racionais não negativos
Consigo fazer 11 pulseiras
e ainda sobram 8 cm de fio.
Depois de fazer as primeiras pulseiras, a Mariana decidiu comprar mais 4,5 m de fio
de pesca. Quantas pulseiras vai conseguir fazer com este novo fio?
261287 114-131.indd 125 30/05/14 17:56

128. RESOLUÇÃO DE PROBLEMAS
126
1.
A D. Cremilde preparou 3,5 kg de doce de abóbora,
que quer distribuir por frascos de vidro.
Se colocar 250 g em cada frasco, de quantos
frascos vai precisar?
2.
A Susana comprou uma tira autocolante para decorar a sua casa de banho.
A tira é formada por quadrados, todos do mesmo tamanho, e mantém sempre
o mesmo padrão com quadrados azuis e verdes, tal como mostra a figura.
A tira completa tem 4 m de comprimento.
a) Quantos quadrados verdes e quantos quadrados azuis tem a tira completa?
b) Qual é a área de cada quadrado?
3.
Os pais do Manuel ganham 1600 € por mês e gastam 20% desse valor na prestação
da casa. Quanto é a prestação da casa?
4.
A Matilde foi com a mãe comprar
o equipamento para as aulas
de Educação Física. Repara nos preços
que as peças que compraram tinham
antes dos saldos.
Fato de treino: 49,90 €
Sapatilhas: 30 €
Camisola: 12 €
Números racionais não negativos
a) O fato de treino estava com um desconto de 50%. Quanto custou?
b) As sapatilhas tiveram um desconto de 10%. Qual foi o preço final?
c) Pagaram por cada camisola 6 €. Qual foi o desconto das camisolas?
d)
Compraram duas camisolas, um fato de treino, umas sapatilhas e um par de meias
que custou 2,50 €. Quanto gastaram no total?
0,16 m
261287 114-131.indd 126 30/05/14 17:56

129. 6
Comprimento da varanda
Pai 10 passos
Hugo 20 passos
Comprimento do canteiro de rosas
Pai 5 passos
Hugo 10 passos
Largura do canteiro de rosas
Pai 1 passo
Hugo 2 passos
127
a) A varanda tem 8 m de comprimento. Quanto mede um passo do pai?
b) Qual é a área, em metros quadrados, do canteiro de rosas?
c)
O Hugo mediu a largura do portão da garagem e contou 8 passos. Qual é a largura
do portão em metros?
d)
O terreno da casa tem 20 m de comprimento. O Hugo vai medi-lo em quantos passos?
6. Observa a tabela de preços da oficina.
5.
O Hugo e o pai estão a medir com passos várias
distâncias no quintal. Observa os seus registos.
a) Calcula mentalmente:
o preço de 4 pneus 145;
o preço de 4 pneus 155.
b) Para efetuar a mudança de óleo, há dois tipos de óleo disponíveis:
Óleo A (dá para 15 000 km): 45, 90 €.
Óleo B (dá para 10 000 km): 35, 90 €.
Tendo em conta apenas as indicações dadas, qual é a compra mais vantajosa?
c)
O pai da Carolina escolheu o óleo A e decidiu trocar os dois pneus da frente
de tamanho 145. Quanto gastou no total (óleo, mão de obra na mudança de óleo
e pneus)?
d)
Inventa um problema que envolva a ida do pai do Tiago com o seu carro a esta
oficina e resolve-o.
Números racionais não negativos
Mudança de óleo
12,5 €
Pneu 145
59,90 €
Pneu 155
69,90 €
261287 114-131.indd 127 30/05/14 17:56

130. 128
Quociente da divisão inteira, quociente e dízima
Observa o diálogo entre a Maria e o João sobre a operação 7 : 3
1. A partir da análise do diálogo anterior, responde às questões seguintes.
a) Indica o quociente de 17 por 5 e o quociente da divisão inteira de 17 por 5;
b) Indica o quociente de 25 por 3 e o quociente da divisão inteira de 25 por 3;
c) Indica o quociente de 12 por 3 e o quociente da divisão inteira de 12 por 3.
Vamos voltar ao
3
7
Podemos obter uma dízima que é uma aproximação de
3
7
.
Já sabemos que a dizíma terá uma parte inteira igual a 2, porque 2 é o quociente da divisão
inteira de 7 por 3.
Para obter uma aproximação às centésimas, faz-se 7,00 : 3.
700
10
10
1
3
233
7,00
10
10
0,01
3
2,33
2. Observa o número
7
25
.
a) Indica o quociente da divisão inteira de 25 por 7.
b) Determina na forma de dízima o quociente de 25 por 7 com aproximação às centésimas.
Números racionais não negativos
Sim, como a divisão inteira
tem resto, o quociente da
divisão exata é o número
3
7
Quanto é o quociente
da divisão inteira
de 7 por 3?
Hum… O quociente da
divisão inteira de 7 por
3 é 2 (com resto 1).
2,33 é uma aproximação
às centésimas de
3
7
261287 114-131.indd 128 30/05/14 17:56

131. 129
6
Calcula o quociente, aproximado
às centésimas, de 7,3 por 0,6.
Ao terminar o algoritmo, colocam-se as vírgulas de tal modo que o número de casas
decimais do quociente seja igual à diferença entre o número de casas decimais
do dividendo e do divisor. O número de casas decimais do resto será igual ao número
de casas decimais do dividendo.
1. Calcula o quociente, aproximado às centésimas, de 5,2 por 0,3.
2.
Representa na forma de dízima os seguintes números racionais, utilizando o algoritmo
da divisão:
a)
25
55
20
37
b)
25
55
20
37
3.
Numa turma de 21 alunos, registou-se o número de irmãos de cada aluno numa tabela
de frequências.
Números racionais não negativos
Algoritmo da divisão com números decimais para o cálculo
aproximado de quocientes
Acrescentam-se tantos zeros
no dividendo quantos
os necessários para que
a diferença entre o número
de casas decimais do dividendo
e do divisor seja dois
(aproximação às centésimas).
Número
de irmãos
Frequência
absoluta
Frequência
relativa
0 3
2
3
1
1 9
2 7
3 1
4 1
a) Identifica a moda.
b) Completa a tabela de frequências relativas.
c)
Calcula as frequências relativas da distribuição do número de irmãos,
em percentagem arredondada às décimas.
12,16 é uma aproximação às centésimas
do quociente de 7,3 por 0,6. O resto é 0,004.
7,300
13
100
40
0,004
0,6
12,16
261287 114-131.indd 129 30/05/14 17:56

132. 130
REVISÃO
1. A Carolina dividiu uma fita em 4 pedaços iguais.
a) Que parte da fita representa cada pedaço?
b)
Sabendo que a fita mede 8,4 m, quanto mede cada pedaço?
2.
A mãe da Marta comprou 11 m de tecido para fazer 4 cortinados iguais. Gastou 2,4 m
em cada cortinado. Que quantidade de tecido sobrou?
3.
O Sr. Humberto quer plantar alfaces e batatas na sua horta. Tem duas parcelas
disponíveis e, como gosta muito de alfaces, quer plantar as alfaces na parcela de maior
área.
As duas parcelas disponíveis são retangulares. Uma mede 8 m por 3,4 m e a outra
mede 4,5 m por 5,1 m. Em que parcela deve o Sr. Humberto plantar as alfaces?
261287 114-131.indd 130 30/05/14 17:56

133. 131
6
4. Copia para o teu caderno e completa:
5 ? ?
?
? ?
: 0,1
2 1 3,4 3 3 0,5 1,5 3 3 8 3 1,1
0,25 3 4 1,5 3 6 2,03 1 0,07 2,5 : 5 1,2 3 3
3,1 3 2
3 : 10 1,1 3 4 11 : 2 15 : 2 2,5 3 2 3,1 3 3
4,2 2 2 20 : 8 2,3 3 3 0,1 3 48
7 3 0,1 2,1 1 4,1 30 : 4 28 : 10 2,3 1 3,7 7,1 1 0,6
40 3 0,1 2,5 3 2
13 : 2 7,5 : 3 0,1 3 82 0,91 3 10 26 : 4 0,5 3 5 33 3 0,1 0,75 3 4 5,7 1 1,3 10 : 4
: 0,01
: 10 : 0,1
: 10
34 ? ?
?
? ?
: 0,01 : 0,1
: 1000 310
: 0,1
5. Calcula mentalmente:
a) o preço de 5 chocolates, que custam 0,99 € cada;
b) o preço de 3 borrachas, que custam 0,49 € cada;
c) o preço de 4 kg de batatas, que custam 0,45 € o quilo;
d) o preço de 3 kg de laranjas, que estão a 0,90 € o quilo;
e) o preço de 0,75 kg de nozes, que estão a 4 € o quilo.
6.
O Afonso está a tentar decifrar uma
mensagem que encontrou na primeira
página de um livro que requisitou na
biblioteca. Ele tem de decifrar letra por
letra recorrendo à tabela. Queres tentar
decifrar a mensagem?
Escreve as letras por cima do resultado
respetivo.
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0 B C O A T R D G H J
1 L K U G X S L Y E F
2 U V P F O A V H I R
3 I A J T L U O F H P
4 D Y R H P T K F A N
5 A M V U E E Q I X I
6 O J E D O M O W A R
7 C W L I V N Q S Q F
8 U L T Q L U H P E E
9 I E H S K P F A N K
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
E
261287 114-131.indd 131 30/05/14 17:56

134. 132
7
UNIDADE
Observa a imagem.
Qual é o comprimento e a largura do pátio da escola?
Determina o perímetro do pátio.
Quantos quadrados coloridos serão necessários para pavimentar
todo o pátio?
A Rafaela e os seus
amigos estão
a pavimentar o chão
do pátio da escola
com quadrados
de cartão coloridos
com 1 m de lado.
261287 132-149.indd 132 30/05/14 17:57

135. 133
Pavimentações
Figuras no plano e sólidos geométricos
Utilizando polígonos podemos construir partes de pavimentações.
Pavimentar é revestir o plano sem deixar espaços vazios e sem fazer sobreposições.
INVESTIGA vamos descobrir pavimentações
Utilizando blocos-padrão constrói partes de pavimentações:
com paralelogramos; com triângulos e quadrados; com figuras à tua escolha.
1. Só alguns polígonos regulares permitem uma pavimentação do plano. Assinala-os.
Triângulo equilátero Quadrado Pentágono regular Hexágono regular
2. Observa as seguintes pavimentações.
a) Transforma a pavimentação hexagonal numa pavimentação com triângulos equiláteros.
b ) Transforma a pavimentação triangular numa pavimentação com hexágonos.
3. Observa as seguintes pavimentações.
a) Transforma a pavimentação retangular numa pavimentação com triângulos.
b) Transforma a pavimentação triangular numa pavimentação com retângulos.
Qual destas pavimentações usa apenas polígonos regulares?
261287 132-149.indd 133 30/05/14 17:57

136. 134 Figuras no plano e sólidos geométricos
Visualização
1. Usa um geoplano 5 3 5.
a) Constrói um quadrado de lado 1, como mostra a figura.
Quantos quadrados iguais ao da figura consegues representar
no geoplano?
10 MINUTOS
Com pauzinhos de igual tamanho, a Catarina construiu 3 quadrados,
como mostra a figura.
Movendo apenas dois pauzinhos na construção, transforma-a
noutra em que figurem apenas 2 quadrados.
b) Constrói agora quadrados de lado 2, como mostra a figura.
Quantos quadrados de lado 2 consegues obter?
c)
Faz um estudo semelhante
para quadrados de lado 3
e 4. Copia a tabela para
o teu caderno e regista
as tuas descobertas.
d) Constrói um quadrado com:
8 pregos na fronteira e 5 pregos no interior;
4 pregos na fronteira e 1 no interior;
4 pregos na fronteira e 4 no interior.
2. Quantos triângulos e quantos quadriláteros consegues ver na figura?
Lado do quadrado 1 2 3 4
Número de quadrados
possíveis de construir
261287 132-149.indd 134 30/05/14 17:57

137. 135
7
3.
A tabela contém um código visual criado por sobreposição das figuras numeradas
de 1 a 4 com as figuras assinaladas de A a D. Na tabela, três combinações estão
incorretas. Descobre quais são.
INVESTIGA construções de 4 cubos
Material:
16 cubos de encaixe.
A Fátima e as amigas estão a fazer construções com 4 cubos cada.
Elas pretendem obter todas as construções possíveis com 4 cubos e que respeitem
as seguintes condições:
O contacto entre dois cubos se existir deve
ser uma face inteira. Observa ao lado dois
exemplos de construções incorretas.
Repara que, no exemplo à direita, as duas
construções, apesar de estarem em posições
diferentes, são iguais.
Tenta descobrir quantas construções diferentes
é possível obter com quatro cubos.
Figuras no plano e sólidos geométricos
1
A
B
C
D
2 3 4
261287 132-149.indd 135 30/05/14 17:57

138. 136
1. Usando uma régua, mede o comprimento dos segmentos seguintes.
Comprimento
a)
Regista as medidas junto aos segmentos. Qual é a unidade de medida que usaste?
2. Observa os polígonos.
a) Classifica os polígonos quanto aos seus lados.
b) Imagina que tens de descrever os polígonos A e C a alguém, que, sem os ver, tem
de descobrir quais são os polígonos em questão. Como descreverias cada um deles
sem usar o seu nome?
c) Para cada polígono, mede os comprimentos dos seus lados e determina o seu
perímetro.
3. Observa agora os polígonos, nos quais estão escritos os seus perímetros.
Através da informação das figuras, diz qual é a medida:
da largura do retângulo;
do lado do quadrado.
Perímetro:
16 cm
P
?
Q
R
S
6 cm
Perímetro: 20 cm
A
?
B
C
D
A B
C
D
F
E
A
C
B
D
Comprimento, massa, capacidade, área e volume
261287 132-149.indd 136 30/05/14 17:57

139. 137
Unidades de medida de comprimento
1. Completa:
a) 12 m 5 dm c) 27,2 m 5 cm e) 1,2 dm 5 mm
b) 2,7dm 5 m d) 125 cm 5 m f) 2,24 mm 5 cm
2. A Rita comprou 4 fios. Ordena os seus comprimentos por ordem decrescente.
Observa a régua graduada cujo comprimento total é de 1 metro.
O metro está dividido
em 10 decímetros.
1 m 5 10 dm
1 dm 5
1
10
m 5 0,1 m
1 m 5 10 dm 5 100 cm 5 1000 mm
O metro está dividido
em 100 centímetros.
1 m 5 100 cm
1 cm 5
1
100
m 5 0,01 m
O metro está dividido
em 1000 milímetros.
1 m 5 1000 mm
1 mm 5
1
1000
m 5 0,001 m
2,3 m 3,24 dm 652 mm 23,3 cm
3.
A Maria e o seu pai pretendem vedar o quintal retangular,
que tem as dimensões indicadas na figura.
a) De quantos metros de rede irão necessitar?
b)
A Maria e o seu pai vão a uma loja e pretendem
comprar a rede para vedar o quintal.
Podemos comprar
100 metros de rede.
Sim. Vou pedir
10 decâmetros de rede.
10 decâmetros
são 100 metros? Sim. Um decâmetro
são 10 metros.
1 dam 5 10 m
Será que sobra alguma rede?
1 cm
1 dm
Comprimento, massa, capacidade, área e volume
7
261287 132-149.indd 137 30/05/14 17:57

140. 138
4. No recreio, mede um comprimento de 10 metros
com um metro articulado. Marca as duas
extremidades com giz. Estica e corta um fio
que ligue os dois pontos marcados.
a)
Qual é o comprimento, em decâmetros, do fio?
b)
Faz uma estimativa do comprimento do recreio
da tua escola. Efetua a medição.
5. Em cada situação indica uma unidade de medida que usarias para efetuar a medição.
Estima as medidas e, de seguida, mede usando material adequado
(régua, metro articulado ou fio de 1 dam).
a) Completa a tabela.
Unidades de medida de comprimento
b) Compara as estimativas com as medidas obtidas.
6. Indica duas situações em que recorrerias ao quilómetro para efetuar medições.
Tal como o decâmetro, o hectómetro (hm) e o quilómetro (km) são unidades
de medida de comprimento maiores do que o metro.
1 hm 5 100 m 1 km 5 1000 m
O metro é a centésima parte do hectómetro. 1 m 5
1
100
hm 5 0,01 hm
O metro é a milésima parte do quilómetro. 1 m 5
1
1000
km 5 0,001 km
Não te esqueças!
Unidade
de medida
Estimativa Valor real
Espessura da moeda
de 1 euro
Altura de uma porta
Largura do teu livro
de Matemática
Comprimento de um
muro da tua escola
Comprimento, massa, capacidade, área e volume
261287 132-149.indd 138 30/05/14 17:57

141. RESOLUÇÃO DE PROBLEMAS
7
139
1.
A Rafaela construiu duas caixas de papel com as formas de um cubo e de um prisma
triangular. Para as decorar, cobriu as arestas das caixas com fita verde.
A aresta da caixa cúbica é de 20 cm.
Na outra caixa, cada aresta das faces
triangulares mede 16 cm e as restantes
medem 30 cm cada.
a)
De quantos centímetros de fita
necessitou a Rafaela para cobrir
as arestas de ambas as caixas?
b) Se cada metro de fita custou
30 cêntimos, quanto gastou
a Rafaela? Explica a tua resposta.
2.
A Maria ofereceu um presente ao seu pai.
O presente, em forma de cubo com 25 cm de lado,
foi embrulhado em papel colorido. Para o tornar
mais bonito, a Maria comprou uma fita azul por
3 euros e colocou-a à volta, como mostra a figura.
Para o laço, ela gastou 50 cm de fita.
A partir da informação dada, formula dois
problemas e pede a um colega para os resolver.
Discute com ele a sua resolução.
3. Todos os dias o Luís faz uma caminhada de 200 metros à volta de um lago.
As suas passadas têm cerca de 40 cm.
a)
Quantas passadas tem o Luís de dar para contornar o lago?
b) Ele demora aproximadamente 4 minutos a contornar o lago. Quantos metros
percorre, em média, por minuto?
c) Numa das suas caminhadas, o Luís parou ao fim de 50 m. Que parte do trajeto
ficou por percorrer?
DESAFIO A vedação
O pai do Nélson vai vedar dois lados paralelos do seu quintal quadrado.
Para fixar a rede, colocou em cada lado 10 postes
com distâncias fixas de 2 metros entre si.
a) Qual é o perímetro do quintal?
b) Quantos metros de rede é necessário comprar?
c) Se o pai do Nélson colocar 6 metros de rede por dia, de quantos
dias necessitará para vedar os 2 lados do seu quintal?
25 cm
Comprimento, massa, capacidade, área e volume
261287 132-149.indd 139 30/05/14 17:57

142. 140
1. Constrói, num geoplano 5 3 5, quatro figuras equivalentes, ou seja, figuras com a mesma
área. Regista-as em papel ponteado e indica a sua área, usando como unidade de medida
1 quadrícula.
Área
2. Constrói os três polígonos no teu geoplano e, de seguida, regista-os em papel ponteado.
Usando uma estratégia semelhante à do Nuno, determina a área de cada um deles.
Cálculo de áreas por decomposição de figuras
O Nuno construiu no seu geoplano quatro figuras equivalentes de área 1 quadrícula.
Observa os seus registos.
Geoplano
do Nuno
Cálculo de áreas por enquadramento
Observa agora a estratégia usada pelo Nuno para determinar a área da figura seguinte.
Comprimento, massa, capacidade, área e volume
Registo
em papel
ponteado
A = 1
A = 1
A = 1
1
2
1
2
1
2
1
2
A = 1
Metade
do retângulo
de área 2.
Geoplano
do Nuno
Registo
em papel
ponteado
1
1 1
1 2
A=3
261287 132-149.indd 140 30/05/14 17:57

143. 141
3. Constrói as figuras seguintes no
teu geoplano. Desenha-as no papel
ponteado e determina a área de cada
uma. Explica o teu raciocínio.
4. Constrói novas figuras no teu geoplano. Depois de as desenhares no papel ponteado,
determina a sua área.
5. Em cada alínea, circunda o menor comprimento.
a) 0,82 m 8,1 dm 802 mm 82,5 cm
b) 1,2 km 1022 m 102 dam 100,2 dam
DESAFIO SEQUÊNCIA DE QUADRADOS
Observa a sequência de quadrados construídos em papel quadriculado, em que,
de cada termo para o seguinte, o lado aumenta uma unidade.
a)
Determina o perímetro de cada figura usando como unidade de medida o lado
da quadrícula.
Calcula agora as áreas usando a como unidade de área.
Completa a tabela seguinte.
b) Continuando a sequência, descobre qual é o perímetro da figura E.
c)
Qual é a área do quinto quadrado?
d) Identifica a relação existente entre a medida do lado e a área de cada quadrado.
Explica o teu raciocínio.
Figura A B C D
Perímetro
Área
7
Comprimento, massa, capacidade, área e volume
A B C D
261287 132-149.indd 141 30/05/14 17:57

144. 142
INVESTIGA Áreas com o tangram
Material:
Tangram e espelho
Como podes obter o quadrado, o paralelogramo
e o triângulo médio a partir dos triângulos pequenos?
—
O que podes concluir acerca da área das figuras
obtidas?
Utilizando todas as peças do tangram, constrói um
retângulo.
Qual é a medida de área do quadrado inicial, usando
como unidade de medida:
— o triângulo pequeno;
— o paralelogramo;
— o triângulo grande.
Refere uma figura cuja área possa ser tomada como unidade de medida de modo
que o triângulo grande tenha 2 unidades de área.
É possível construir quadrados
de oito modos diferentes.
Na figura, estão dois exemplos
representados em papel ponteado.
— Tenta descobrir outros 6 modos de construir quadrados.
—
Considerando como unidade de área o triângulo pequeno, agrupa os quadrados
obtidos de acordo com a medida da sua área. Quantos grupos se formaram?
Utilizando um espelho e um triângulo pequeno, faz experiências para veres que
peças do tangram consegues obter.
—
Experimenta agora com o quadrado e depois com o paralelogramo.
Com o espelho, descobre quantos eixos de simetria tem cada peça do tangram.
Área
10 MINUTOS
Faz duas construções a teu gosto com as peças do tangram.
Calcula a sua área, usando como unidade de medida o triângulo pequeno.
Comprimento, massa, capacidade, área e volume
261287 132-149.indd 142 30/05/14 17:57

145. 143
1.
O quadrado que vês desenhado
mede 1 dm de lado e está dividido
em quadrados mais pequenos.
Unidades de medida de área
O cm2
é a área de um quadrado com 1 cm de lado.
Observa como a Maria e a Teresa determinaram a área da figura.
Maria: Cada quadrado tem 1 cm2
e a figura é composta por 6 quadrados.
A área é de 6 3 1 cm2
, ou seja, 6 cm2
.
Teresa:
A figura tem 2 linhas e cada linha tem 3 quadrados
com 1 cm2
.
A área é de 2 3 3 cm2
, ou seja, 6 cm2
.
1
cm2
1 cm
1 cm
a)
Quanto mede o lado de cada
quadrado mais pequeno?
b)
Qual é a área do quadrado,
em cm2
?
c)
Quantos cm2
há no dm2
?
d)
Que parte do dm2
é o cm2
?
2. Constrói com os teus colegas vários quadrados em cartolina com 1 dm2
de área. Afixem-nos
na parede da sala de aula, de modo a construírem um quadrado com 1 m de lado.
7
Comprimento, massa, capacidade, área e volume
a) Quantos dm2
há no m2
?
b) Que parte do m2
é o dm2
?
3.
Qual é a unidade de medida que usarias para determinar a área:
a) de uma folha de papel; c) da superfície da tua borracha;
b) do tampo da secretária do professor; d) da tua sala de aula.
Um quadrado com 1 dm
de lado tem 1 dm2
de área.
Não te esqueças!
Um quadrado com 1 m de lado tem 1 m2
de área.
Não te esqueças!
1 cm
1 cm
1
cm2
261287 132-149.indd 143 30/05/14 17:57

146. 144 Comprimento, massa, capacidade, área e volume
Unidades de medida de área
O casal Matias pretende comprar um terreno para a construção de uma moradia.
Depois de consultarem a página dos classificados, selecionaram os anúncios seguintes:
Terreno A Terreno B
1. Converte:
a) 230 m2
5 cm2
c) 1,35 hm2
5 m2
b) 65 cm2
5 dm2
d) 12,4 dm2
5 dam2
2.
O chão do pátio da escola vai ser pintado de verde e a fachada
principal vai ser pintada de branco. Cada litro de tinta
(verde ou branca) dá para pintar 10 m2
.
a)
Qual é a cor da tinta mais necessária?
Explica como pensaste.
b)
Quantos litros de tinta de cada cor necessitam
de comprar?
c) Cada litro de tinta branca custa 5 € e cada litro de tinta
verde custa 6 €.
Quanto dinheiro irá gastar a escola com a compra da tinta?
Para comparar as medidas das áreas dos dois terrenos, cada um pensou de forma diferente.
Ele converteu 2,5 dam2
em m2
:
E ela fez o seguinte registo:
Ambos concluíram que o terreno A era maior.
km2
hm2
dam2
m2
dm2
cm2
mm2
2 5 0
2,5 dam2
5 250 m2
km2
hm2
dam2
m2
dm2
cm2
mm2
3 0 0
300 m2
5 3 dam2
90 m2
2,44 dam2
261287 132-149.indd 144 30/05/14 17:57

147. 145
7
Comprimento, massa, capacidade, área e volume
Medidas agrárias
O are, palavra derivada de «área», é uma medida agrária e equivale ao decâmetro quadrado.
1 a 5 1 dam2
1. Converte nas unidades indicadas.
a) 15 dam2
5 a b) 20 hm2
5 a c) 1200 m2
5 a
Vês o meu quintal?! Eu e o meu pai
estivemos a medir e descobrimos
que tem 100 m2
.
Muito bem.
Tem 1 are de área.
As outras duas medidas agrárias são:
miriare hectare are centiare
1 ma 1 ha 1 a 1 ca
1 km2
1 hm2
1 dam2
1 m2
2. Quantos hectares tem um terreno com 13 450 m2
?
centiare (centi 1 are)
100 vezes menor do que o are
1 ca 5 1 m2
miriare (miria 1 are)
10 000 vezes maior do que o are
1 ma 5 1 km2
Repara na unidade usada no título do jornal.
Usaram o hectare (hecto + are), que é a medida agrária
mais comum para a medição de terrenos agrícolas.
Observa:
hectare (hecto+are) é 100 vezes maior
do que o are.
1 ha 5 1 hm2
5 10 000 m2
10 m 10
m
261287 132-149.indd 145 30/05/14 17:57

148. 146
1. Determina, em metros quadrados, a área de cada uma das figuras.
Área de um retângulo
INVESTIGA como calcular a área de retângulos
Material:
Papel quadriculado (quadrícula com 1 cm de lado)
Lápis
Régua
Como fazer:
Desenha, no papel quadriculado, todos os
retângulos com 20 cm de perímetro, sendo
as medidas dos seus lados números inteiros.
Usando a quadrícula como unidade de medida (1 cm2
), determina a área de cada
retângulo. Explica como chegaste à tua resposta.
a) Copia a tabela para o teu caderno e completa-a.
Perímetro
(em cm)
Comprimento (c)
(em cm)
Largura (l)
(em cm)
Área
(em cm2
)
20
20
20
20
20
b) Existe alguma relação entre as medidas do comprimento e da largura
e a medida de área de cada retângulo? Regista no teu caderno as tuas
conclusões.
c) Consegues identificar uma regra para o cálculo da área de um retângulo
através das medidas do comprimento e da largura?
Regista-a. Constrói novos retângulos e testa a tua conjetura.
d) Qual dos retângulos tem maior área?
e) Consegues agora identificar uma regra para o cálculo da área de um quadrado
através da medida do seu lado? Regista-a. Constrói novos quadrados e testa
a tua conjetura.
Comprimento, massa, capacidade, área e volume
6 m
6
m
8 m
3
m
3 m
4 m
2
m
5
m
6 m
6
m
8 m
3
m
3 m
4 m
2
m
5
m
1 m
78,4 cm
261287 132-149.indd 146 30/05/14 17:57

149. 147
2. Observa o painel e responde às questões.
a)
Relativamente à área do painel, qual é a região
cuja área é:
50%
1
6
2
24
25%
b) Qual é a área de cada região, usando como unidade de medida ?
3.
O terreno do Sr. Joaquim mede 560 m2
de área
e tem de comprimento 40 m. Quanto mede a largura
do terreno?
DESAFIO quintal da Joana
A Joana pretende determinar a área de todos
os canteiros do seu quintal. Como vês na figura
ao lado, o quintal é constituído por:
dois canteiros, B e D, ambos com a forma
de um quadrado;
dois canteiros, A e C, ambos retangulares.
Depois de algumas medições, a Joana registou
na figura a área de três canteiros.
Conseguirá a Joana determinar a área do canteiro C sem efetuar mais medições?
Se sim, calcula-a e explica o teu raciocínio.
DESAFIO Tabuleiro de xadrez
O António, jogador de xadrez, possui um tabuleiro
constituído por pequenos quadrados brancos
e pretos.
No seu tabuleiro, cada quadrado mede 4 cm
de lado.
a)
Qual é a área do tabuleiro excluindo
as margens?
b)
Qual é a área ocupada pelos quadrados
brancos?
c) Que relação existe entre as duas medidas?
7
Comprimento, massa, capacidade, área e volume
A
28 m2
C
B
16 m2
D
9 m2
261287 132-149.indd 147 30/05/14 17:57

150. 148
1. Para cada caso escolhe a medida que te parece mais plausível.
a) Comprimento de uma mesa (em cm): 1,5 ou 15 ou 150
b) Espessura de um espelho (em mm): 0,3 ou 3 ou 30
c) Distância entre Porto e Lisboa (em km): 314 ou 31,4 ou 3,14
d) Comprimento de uma sala de aula (em dam): 12 ou 1,2 ou 120
2.
A D. Rosa quer pavimentar um caminho com 9 m de comprimento e 150 cm de largura.
REVISÃO
a)
Qual é o perímetro do passeio?
b)
Qual é a sua área?
c) Conseguirá a D. Rosa pavimentar exatamente o passeio com mosaicos retangulares
de 30 cm por 50 cm? Explica como pensaste.
3.
O Filipe pretende desenhar um retângulo com 12 cm2
de área, e quer que os
comprimentos dos seus lados, em centímetros, sejam números inteiros.
a)
Haverá apenas uma possibilidade? Averigua fazendo construções no papel
quadriculado de 1 cm de lado.
b) Determina os seus perímetros. O que podes concluir?
4.
Uma piscina retangular possui 1200 m2
de área. A piscina tem várias pistas com
3 m de largura cada uma. O comprimento da piscina é de 50 m.
a) Qual é a largura da piscina?
b) Quantas pistas tem a piscina?
c) Se optassem por construir as pistas com 6 m de largura, quantas seria possível
construir?
5. Completa:
a) 2 km 5 m c) 34 cm 5 m e) 77,6 mm 5 m
b) 3 m2
5 cm2
d) 3 dm2
5 m2
f) 150 cm2
5 m2
9 m
150 cm 50 cm
30 cm
261287 132-149.indd 148 30/05/14 17:57

151. 149
7
6. No teu geoplano representa, para cada uma das alíneas seguintes, uma figura que
obedeça a cada condição. Depois, reproduz essas figuras no papel ponteado.
a)
Um triângulo com um ângulo reto e nenhum prego no interior.
b)
Dois polígonos diferentes com o mesmo perímetro.
c)
Dois polígonos diferentes com a mesma área.
d)
Um polígono com oito pregos na fronteira, um no interior, todos os lados com
o mesmo comprimento e os lados opostos paralelos.
7.
Observa os polígonos seguintes.
a)
Determina a área de cada figura em .
b) Copia para o teu caderno e traça com um lápis de cor os eixos de simetria de cada
figura.
8.
Uma das paredes da sala da Beatriz foi coberta
com um papel liso.
As dimensões estão registadas na figura.
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
a)
Quantos cm2
de papel foram necessários para cobrir a parede?
b)
Um rolo de papel mede 6 m2
. Só se vendem rolos inteiros. Quantos rolos foram
necessários para cobrir a parede?
A B C
7 m
480 cm
300 cm
1,8 m
261287 132-149.indd 149 30/05/14 17:57

152. 150
8
UNIDADE
Para a festa, a professora vai preparar um bolo de bolacha para
24 crianças.
Quem é que está encarregado de levar o açúcar?
Qual é a quantidade de margarina que a Inês tem de levar para
a escola?
Quantos ovos são necessários?
A Bruna vai levar para a escola um termo com 1 litro de café.
Será suficiente?
Para a festa de final de ano, a turma da Maria está a organizar um lanche.
Hoje a professora está a definir quem irá trazer para a escola cada um
dos ingredientes necessários para o bolo de bolacha.
Bolo de bolacha (para 6 pessoas)
Ingredientes:
150 g de açúcar — Ana
250 g de margarina — Inês
4 ovos — Marcelo
250 g de bolacha — Nuno
1 cL de café — Bruna
261287 150-165.indd 150 30/05/14 17:58

153. 151
Volume
Comprimento, massa, capacidade, área e volume
INVESTIGA Esferas de plasticina
Material:
3 copos iguais e transparentes
Água
3 porções de plasticina com tamanhos
diferentes
Marcador
Como fazer:
Dispõe os 3 copos em fila na tua mesa
e coloca uma porção igual de água em
cada um deles (o nível da água deve corresponder aproximadamente ao meio
do copo). Com o marcador, marca o nível de água nos 3 copos.
Constrói 3 esferas de plasticina de tamanhos diferentes. Introduz
cada uma num copo diferente.
Com o marcador, regista novamente o nível de água em cada um dos copos.
— Depois de teres introduzido as esferas de plasticina nos copos, o que observaste?
— Consegues encontrar uma razão para a subida do nível da água?
—
Por que razão há diferenças entre os 3 copos?
Regista no teu caderno as conclusões obtidas.
Retira as esferas de dentro dos copos. Ordena-as de acordo com a quantidade
de espaço que ocupam.
Com plasticina, faz duas novas construções que, na tua opinião, ocupem a mesma
quantidade de espaço, ou seja, tenham o mesmo volume. De que forma podes
averiguar se ambas ocupam o mesmo espaço?
1.
A Diana tem berlindes de dois tipos (A e B). Após colocar a mesma quantidade de água
em copos iguais, ela mergulhou um conjunto de 10 berlindes do tipo A num copo e um
conjunto de 5 berlindes do tipo B noutro. Observa as imagens.
a)
Compara a quantidade de espaço ocupada pelos dois conjuntos de berlindes.
b)
Qual é o tipo de berlinde que tem maior volume? Explica como chegaste à tua
resposta.
Tipo A Tipo B
261287 150-165.indd 151 30/05/14 17:58

154. 152 Comprimento, massa, capacidade, área e volume
2. Coloca na tua mesa de trabalho 8 cubos de encaixe de aresta 1.
a)
Com todos os cubos, constrói sólidos com formas diferentes.
b) Os sólidos têm o mesmo volume? Porquê?
Volume
c)
Constrói dois sólidos não equivalentes. Determina os seus volumes.
3.
Observa os sólidos seguintes.
a)
Usando o como
unidade de volume, determina o volume de cada sólido.
b)
Para calcular o volume de dois dos sólidos, o Hugo apresentou as expressões que se
seguem. Completa com a letra que identifica cada sólido:
Dois sólidos que ocupam a mesma quantidade de espaço são sólidos equivalentes.
Neste caso, o volume de cada sólido é 8 unidades cúbicas .
Não te esqueças!
d) Determina a área da superfície dos sólidos B e C usando como unidade de área.
Área da superfície de um sólido
A área da superfície de um sólido é a soma das áreas das faces
desse sólido.
A Ana e o Ivo determinaram a área do sólido A, usando como
unidade de área cada quadradinho ( ).
Ana: A área total das 3 faces visíveis é 16 e a área total das 3 faces
não visíveis é 16 . A área da superfície do sólido A é de 32 .
Ivo: As áreas de cada face são: frente: 4 atrás: 4 cima: 6
baixo: 6 direita: 6 esquerda: 6 .
A área da superfície do sólido A é de 32 (4 1 4 1 6 1 6 1 6 1 6).
Não te esqueças!
4
6
6
A B C
c) Para cada sólido, explica porque podes calcular o volume usando a expressão anterior.
Sólido A
Volume do sólido : (2 3 3) 3 2 Volume do sólido : 3 3 3 1 2
261287 150-165.indd 152 30/05/14 17:58

155. 153
8
Comprimento, massa, capacidade, área e volume
1.
Considera os sólidos de A a H.
Visualização espacial
Observa o sólido e as respetivas vistas.
a)
Completa a tabela seguinte com a letra do sólido que corresponde a cada
combinação da vista de cima com a vista de frente. Vê o exemplo.
b) Determina o volume e a área da superfície dos sólidos C, D e H usando como
unidades o e o , respetivamente. Identifica sólidos equivalentes.
Vista de cima
Vista
de frente
Sólido G
Vista de frente Vista de lado Vista de cima
Vista de cima
Vista de lado
Vista de frente
DESAFIO O cubo mergulhado
O Alexandre mergulhou um cubo constituído por pequenos cubinhos ( ) numa lata
de tinta vermelha. Deixou secar e de seguida desmontou-o.
Observa as imagens.
Diz quantos cubos pequenos ( ) ficaram com:
—
três faces pintadas; duas faces pintadas;
uma face pintada; nenhuma face pintada.
A H
B C D E F G
261287 150-165.indd 153 30/05/14 17:58

156. 154
1. Observa a sequência de figuras.
Comparação e estimativa de volumes
a) Completa a tabela.
b) Determina uma possível regra de formação e, de acordo com essa regra, determina
o volume, em , da próxima figura desta sequência.
c)
Se usasses as peças da tabela, para construíres os sólidos, precisarias do mesmo
número de peças? Completa a tabela.
d) Explica por que razão os números em cada coluna não são todos iguais.
e) Relaciona as medidas de volume dos sólidos com as unidades de medida usadas.
DESAFIO Encaixotando cubos
Depois de brincar com os seus cubos, a Joana guarda-os em caixas.
Se colocar 7 cubos em cada caixa, sobram 3 cubos.
Se colocar 8 cubos em cada caixa, sobra apenas um 1 cubo.
Quantos cubos poderá ter a Joana? Explica como pensaste.
Comprimento, massa, capacidade, área e volume
A B C
A B C
Volume em
Área da superfície em 32
A B C
Unidade
de volume
1 cubo
2 cubos
Meio cubo
261287 150-165.indd 154 30/05/14 17:58

157. 155
8
1.
Supõe agora que fazes a construção de um cubo com 1 m
de aresta, tal como o da figura.
O volume do cubo é 1 m3
.
a) Quantos decímetros cúbicos tem o cubo?
b) Copia para o teu caderno e completa:
1m3
5 dm3
2.
Completa:
a) 1200 cm3
5 dm3
c) 5 m3
5 dm3
b) 5500 dm3
5 m3
d) 0,350 m3
5 dm3
3.
Observa o exemplo seguinte.
Unidades de medida de volume
A Mariana construiu uma representação de um cubo
com 1 dm de lado. Constrói também uma.
Numa cartolina desenha 6 quadrados de 1 dm2
de área. Recorta-os e, com fita-cola, une-os de forma
a formar um cubo.
O volume do cubo é 1 dm3
.
É um cubo com 1 dm de aresta.
Observa o comentário da Mariana.
Portanto: 1 dm3
5 1000 cm3
Comprimento, massa, capacidade, área e volume
1 dm3
1 m
Cada aresta está dividida
em 10 cm.
Na base do cubo é possível
dispor 100 cubos de 1 cm3
.
Como o cubo leva
10 camadas de cubinhos
iguais à base, o cubo leva
1000 cubinhos de 1 cm3
.
A imagem está reduzida.
1 dm3
1 m
Converte 4230 dm3
em dam3
.
km3
hm3
dam3
m3
dm3
cm3
mm3
2 3 5 0 0
23,5 dam3
5 23 500 m3
261287 150-165.indd 155 30/05/14 17:58

158. 156 Comprimento, massa, capacidade, área e volume
Volume de um paralelepípedo
1.
Observa a sequência de cubos com 1 cm, 2 cm e 3 cm de arestas, e assim sucessivamente.
a) Completa a tabela.
Aresta (em cm) 1 2 3 4
Volume (em cm3
)
Estratégia
de cálculo
2 3 2 3 2
Total 8
b)
Identifica a relação existente entre a medida da aresta e o volume de cada cubo.
Explica o teu raciocínio.
c)
Através da relação encontrada determina o volume do cubo com 12 cm de aresta.
INVESTIGA Construindo caixas sem tampa
Material:
5 folhas de papel quadriculado com quadrículas de 2 cm de lado; cerca de 50 cubos
com 2 cm de aresta; tesoura; fita-cola
Como fazer:
Recorta as folhas de papel quadriculado de modo a obteres retângulos
de 9 por 11 quadrículas. Quantas quadrículas tem cada retângulo?
Num retângulo, corta uma quadrícula em cada canto e dobra as bandas de modo
a formar uma caixa. Cola as arestas com fita-cola. Obtiveste a caixa 1.
a)
Quantos cubos cabem dentro da caixa?
Regista a tua estimativa.
b)
É necessário enchê-la com cubos para o saber?
Se não é necessário, que estratégia podes usar?
c) Testa a tua estratégia enchendo a caixa com cubos.
Compara o resultado com a tua estimativa.
caixa 1
261287 150-165.indd 156 30/05/14 17:58

159. 157
Comprimento, massa, capacidade, área e volume
8
Constrói agora uma caixa com duas quadrículas de altura. Quantas quadrículas
terás de recortar em cada canto? Obtém, assim, a caixa 2.
a)
Qual é a estimativa do número de cubos que cabem na caixa 2? Regista-a.
b)
Indica uma estratégia possível para determinar o volume da caixa. Enchendo
a caixa com os cubos, testa se a tua estratégia está correta.
c)
Completa a tabela na linha da caixa 2.
Constrói as caixas com três e quatro quadrículas de altura: serão as caixas 3 e 4.
Faz para estas novas caixas um estudo semelhante ao que fizeste para as caixas
anteriores e completa as linhas correspondentes da tabela do teu caderno.
Observando a tabela, o que acontece ao comprimento, à largura e ao volume,
à medida que se faz cada caixa nova? E o que acontece à altura? Discute as tuas
conclusões com os teus colegas.
Compara as três colunas do comprimento, da largura e da altura com a coluna
do volume. Consegues identificar alguma relação entre as três primeiras medidas
e a medida do volume de cada caixa?
Comprimento
(unidades)
Largura
(unidades)
N.º
de cubos
da base
(área
da base)
Altura
(número
de camadas
de cubos
unitários)
Volume
(número de cubos
unitários necessários
para encher a caixa)
Número total
de quadrados
unitários
cortados do
retângulo
Contagens Total
Caixa 1
Caixa 2
Caixa 3
Caixa 4
Copia para o teu caderno a tabela de registos seguinte e completa a linha
correspondente à caixa 1.
8 cm
4 cm
3 cm
2.
A Mariana está agora a organizar os seus cubinhos
de 1 cm3
de volume numa caixa com a forma de um
paralelepípedo. De acordo com as dimensões
da caixa, responde às questões.
a) Quantos cubos cabem na caixa?
b) Qual é o volume da caixa?
c) Converte o volume da caixa para dm3
.
261287 150-165.indd 157 30/05/14 17:58

160. 158 Comprimento, massa, capacidade, área e volume
1.
As figuras seguintes representam as vistas de frente, de lado e de cima
de um determinado sólido constituído por pequenos cubos ( ).
Volume
vista de frente vista de lado vista de cima
Vista de frente Vista de lado Vista de cima
a) De acordo com as vistas apresentadas e usando pequenos cubos (por exemplo,
cubos de encaixe), constrói o sólido.
b) Completa:
Área da superfície do sólido: ( ) Volume do sólido: ( )
c) Desenha um novo sólido, usando o mesmo número de cubos que usaste no anterior.
d) Desenha, no quadriculado, as vistas do sólido que construíste:
Área da superfície do sólido: ( ) Volume do sólido: ( )
2.
Observa a figura que representa uma planificação
de um prisma reto.
a)
Qual é o nome do prisma?
b) Completa:
N.º de faces: N.º de arestas:
N.º de vértices:
c) Faz as medições que achares necessárias e calcula,
em cm3
, a medida do volume do prisma.
Explica como pensaste.
261287 150-165.indd 158 30/05/14 17:58

161. 159
Comprimento, massa, capacidade, área e volume
8
1.
Observa os recipientes e lê as frases com atenção.
Unidades de medida de capacidade
A capacidade do balde é tripla
da capacidade do jarro.
A capacidade da caneca é um quinto
da capacidade do jarro.
A capacidade da caneca é o dobro
da capacidade do copo.
a)
Constrói um gráfico de barras com a informação relativa à capacidade de cada
recipiente.
b) Quantos copos de água são necessários para encher o balde?
A unidade principal de medida de capacidade é o litro (L).
Outras unidades de medida de capacidade são:
o decilitro (dL), o centilitro(cL) e o mililitro(mL);
1 L 5 10 dL 1 L 5 100 cL 1 L 5 1000 mL
o decalitro (daL), o hectolitro (hL) e o quilolitro (kL).
1 L 5 0,1 daL 1 L 5 0,01 hL 1 L 5 0,001 kL
Não te esqueças!
2.
Observa a tabela seguinte, em que se regista a informação relativa ao consumo de água
numa empresa durante uma semana.
a)
Em que dia da semana se consumiu menos água? E mais água?
b)
Qual é a diferença, em centilitros, entre a 2.ª-feira e a 4.ª-feira?
c)
Sabendo que a empresa paga por cada litro de água 0,25 euros,
calcula quanto gastou a empresa no consumo de água nesta
semana.
Dia da
semana
2.ª-feira 3.ª-feira 4.ª-feira 5.ª-feira 6.ª-feira Sábado Domingo
Consumo 31 L 23 L 21 L 14 L 20 L 23 dL 34 dL
261287 150-165.indd 159 30/05/14 17:59

162. 160 Comprimento, massa, capacidade, área e volume
Massa
A unidade de medida principal de massa é o quilograma (kg).
Outras unidades de medida de massa são:
o grama (g) 1 kg 5 1000 g
o miligrama (mg) 1 g 5 1000 mg
a tonelada (ton) 1 ton 5 1000 kg
Outras unidades de medida menos usadas (submúltiplos do quilograma) são:
o decagrama (dag) e o hectograma (hg) — superiores ao grama
1 kg 5 100 dag 1 kg 5 10 hg
o decigrama (dg) e o centigrama (cg) — inferiores ao grama
1 g 5 10 dg 1 g 5 100 cg
1.
Observa as balanças.
Indica a unidade de medida (ton, kg, g) em que te parece que o peso de cada um
dos objetos representados foi medido.
2.
Completa com os símbolos ,, ., 5.
a) 500 g 450 g c)
1
4
kg 250 g
b) 750 g 0,5 kg d) 1000 g
3
4
kg
10 MINUTOS
Coloca por ordem crescente de peso:
0,75 kg 720 g 748,5 g 727 400 mg
B C
Algodão
261287 150-165.indd 160 30/05/14 17:59

163. 161
Comprimento, massa, capacidade, área e volume
8
1.
A Márcia tem um tanque cúbico vazio com 2 m de lado interno.
a) Se ela pretender encher o tanque, de quantos litros de água necessitará?
b) Se o tanque vazio pesar 20 kg, quanto pesa o tanque cheio de água?
2. Circunda a opção correta.
A capacidade de um cubo com 8 cm de aresta é:
inferior a 1 dm3
superior a 1 dm3
igual a 1 dm3
Relação entre volume/capacidade e entre massa/capacidade
INVESTIGA Capacidade de uma caixa cúbica
Material:
Cubo com 1 dm de aresta (construído anteriormente)
Pacote de sumo de 1 L
Arroz
Água
Como fazer:
Compara a caixa cúbica com o pacote de sumo e faz uma estimativa da capacidade
da caixa.
Enche a caixa com arroz. Quantos dm3
de arroz leva a caixa?
Despeja o arroz da caixa para o pacote de sumo. O que aconteceu?
— Quantos litros de arroz leva o pacote de sumo?
—
Quantos litros de arroz leva a caixa cúbica, ou seja, qual é a capacidade em litros
de uma caixa com 1 dm de lado?
10 MINUTOS
Com 10 L de água, quantos recipientes é possível encher, se cada um tiver de volume
interno, aproximadamente:
a) 1 dm3
b)
1
2
dm3
c) 2 dm3
d) 10 dm3
O litro é a capacidade de um recipiente com 1 dm3
de volume interno.
1 dm3
5 1 L
1 m3
5 1000 L
Não te esqueças!
Com a ajuda de uma balança, determina o peso do pacote vazio de sumo.
Enche o pacote de sumo com água e pesa-o novamente.
Quanto pesa 1 litro de água? Explica como pensaste.
261287 150-165.indd 161 30/05/14 17:59

164. RESOLUÇÃO DE PROBLEMAS
162
162 Comprimento, massa, capacidade, área e volume
1.
Um fabricante de bolas de ténis organiza-as, para venda,
em caixas cúbicas com 8 cm de lado. Como a figura ao lado
mostra, as bolas estão todas encostadas umas às outras.
A caixa possui uma faixa verde que passa pelo centro
de cada face lateral da caixa.
a) Quantas bolas cabem em cada caixa?
b) Qual é, em cm3
, o volume da caixa?
c)
Se a caixa tivesse o triplo do comprimento,
quantas bolas caberiam na caixa?
Explica como pensaste.
d)
Observa a planificação seguinte da caixa
cúbica. Desenha, com um lápis, uma linha que
corresponda à faixa verde representada nas faces
laterais.
e) Completa:
Comprimento da faixa: cm.
Área da base: cm2
.
2.
O Sr. Telmo, com a colheita de uvas do ano passado,
produziu 1800 litros de vinho
branco e pretende agora engarrafar
3
2
dessa produção.
a)
Que quantidade de vinho, em litros, pretende
engarrafar?
b)
Se ele utilizar garrafas com capacidade
de 0,5 litros, de quantas garrafas necessitará?
c)
Se as garrafas tiverem o dobro
da capacidade, de quantas garrafas
necessitaria?
d)
Completa a seguinte tabela
e investiga a relação que existe entre
o número de garrafas necessárias
e a capacidade de cada garrafa.
base
Capacidade
de cada garrafa
N.º de garrafas
necessárias
0,5 L
1 L
2 L
4 L
3.
Considera um recipiente cúbico de metal com 0,5 m de lado.
a)
O volume do recipiente é: 1,25 dm3
1,5 dm3
125 dm3
125 m3
b)
Qual é a quantidade máxima de água, em litros, que se pode armazenar no
recipiente?
261287 150-165.indd 162 30/05/14 17:59

165. 8
163
163
4.
A Rafaela foi à frutaria comprar nêsperas. Observa a imagem seguinte.
a) No teu caderno, completa a tabela relativa à relação peso/preço na compra
de nêsperas.
b)
A Rafaela comprou 2,5 kg de nêsperas. Quanto pagou?
c) Depois, voltou à frutaria e pagou por um saco de nêsperas 6 €.
Quantos quilogramas de nêsperas comprou?
5.
O Sr. Fernando faz transportes com a sua
carrinha. O peso máximo que a carrinha pode
transportar é 6 toneladas.
a)
Se pretender levar ao cliente A uma carrinha
de sacos de cimento de 40 kg cada, quantos
sacos poderá carregar?
b)
Se, para o cliente B, ele levar sacos de cimento
de 25 kg, quantos sacos poderá levar?
c)
Observa os preços de cada saco. Se se pretende
comprar uma grande quantidade de cimento, qual
é o tipo de saco mais económico? Explica o teu
raciocínio.
6.
A Maria comprou 1 kg de massa e 250 g de fiambre.
Observa a imagem.
a) Quanto pagou a Maria pelas suas compras?
b)
A família da Maria come 50 g de fiambre por dia.
Para quantos dias dará a quantidade de fiambre
que a Maria comprou?
Peso (em kg) 1 2 4 5 10
Preço (em euros)
0,90 € 8 €/kg
Comprimento, massa, capacidade, área e volume
261287 150-165.indd 163 30/05/14 17:59

166. 164
a) Qual é a diferença de peso entre a mochila mais pesada e a mais leve?
b) Quanto pesam, em gramas, as mochilas do Pedro e do Bernardo juntas?
c) Faz uma estimativa do peso total das 4 mochilas. Comenta a razoabilidade dessa
estimativa.
2.
Observa os recipientes. Seleciona a opção que te parece aceitável
para a capacidade:
a) da lata: 33 cL ou 1 cL ou 8 dL
b) da garrafa: 2 L ou 0,5 L ou 50 hL
c) do garrafão: 50 dL ou 10 dL ou 1 L
3.
O Sr. Mário produziu no ano passado 1575 L de azeite.
a)
Se o armazenar em vasilhas de 50 L, de quantas
vasilhas necessitará?
b)
Se engarrafar 80 garrafões de 5 L e vender cada litro a 4 €, quanto receberá?
4. Observa as balanças e responde às questões.
a)
Se todas as maçãs pesam aproximadamente o mesmo, quanto pesa cada maçã?
E 6 maçãs?
b)
Se cada quilograma
de maçãs custar
1,20 €, quanto
custam 6 maçãs?
c)
Se cada ananás pesa
o quádruplo de cada
pera, quantas peras
é necessário colocar
no prato da direita para equilibrar a balança?
d) Se cada pera pesa 200 g, quanto pesa um ananás?
1. Observa o peso de cada uma das mochilas de 4 amigos.
REVISÃO
1,2 kg 0,9 kg 2,2 kg 1800 g
261287 150-165.indd 164 30/05/14 17:59

167. 165
8
6.
O Sr. Santos embala computadores portáteis em caixas com 1 m3
de volume.
Cada caixa leva 120 portáteis. Hoje ele tem 8 caixas para transportar.
a)
Qual é o volume das 8 caixas?
b)
Sabendo que as caixas estão todas cheias, qual é a quantidade
de computadores portáteis embalada?
c)
Conseguirá o Sr. Santos transportar todas as caixas num só contentor com 3 m de
comprimento, 1 m de altura e 2 m de largura? Explica como chegaste à tua resposta.
d)
Quais são as dimensões do contentor se ele pretender transportar 15 caixas sem
que o contentor fique com espaços vazios? Haverá apenas uma hipótese? Explica
como chegaste à tua resposta.
7.
A Inês fez alguns bolos de laranja para a sua festa de aniversário.
a)
Para fazer cada bolo de laranja, a Inês precisa de 2 dL de leite.
Como usou 1,6 L de leite, quantos bolos de laranja fez?
b)
Se cada bolo levou
1
4
kg de farinha, de quantos
quilogramas necessitou a Inês para fazer todos os bolos de laranja?
8. Observa as seguintes medidas de massa:
500 g 2 kg 100 g 10 g 5 kg
Associa a cada objeto, a medida que poderá corresponder ao seu peso.
A B C D
5. Calcula o volume das duas caixas representadas.
A
B
3 m
2 m
5 m
2 m
3,2 m
41 dm
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
261287 150-165.indd 165 30/05/14 17:59

168. 166
9
UNIDADE
Reproduz esta calçada utilizando blocos-padrão.
Cria outros motivos com este material.
261287 166-176.indd 166 30/05/14 18:00

169. 167
No teu caderno, de acordo com essa regra, continua a sequência para o lado esquerdo,
desenhando seis figuras.
3.
Observando a sequência pensa numa possível regra de formação e, de acordo com essa
regra, completa a sequência no teu caderno.
Sequências e regularidades
1.
Imagina que te pediam para construíres uma sequência, repetindo o seguinte grupo
de polígonos, sucessivamente, por esta ordem.
a) Continua-o, no teu caderno, até teres 20 figuras.
b)
De acordo com a regra de formação da sequência, substitui cada polígono por uma
letra (ao mesmo polígono corresponde a mesma letra), até teres 20 letras. Podes
começar assim:
A A
2. Observa a sequência e determina uma possível regra de formação.
4.
Para a sequência seguinte determina uma possível regra de formação e, de acordo com
essa regra, escreve os três números seguintes.
Compara a tua sequência com as dos teus colegas.
1 2 4
Regularidades
261287 166-176.indd 167 30/05/14 18:00

170. 168
Regularidades numéricas
1.
Observa as sequências numéricas e, para cada uma, pensa numa possível regra utilizada
para a construir.
a)
Em cada sequência, escreve os quatro números seguintes,
de acordo com essa regra.
Regularidades
b) No final, compara as tuas respostas com as dos teus colegas.
2.
Pensa numa regra e, de acordo com ela, constrói uma sequência com quatro números.
Troca com o teu colega e, enquanto ele tenta descobrir a regra em que pensaste, tenta
descobrir a dele.
3. Observa o triângulo de Pascal.
a)
Regista algumas das regularidades que consegues
encontrar.
b)
Soma os números adjacentes de cada linha
e descobre se existe alguma regularidade.
c)
Copia para o teu caderno e completa
o que falta.
1
1 1
1
2
1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
4.
Observa a sequência e determina uma possível regra de formação; de acordo com essa
regra, escreve os cinco termos seguintes.
1 1 2 2 1 3 3 1 4
23 34 45 56 67
90 81 72 63 54
130 115 100 85 70
51 49 47 45 43
22 25 24 27 26
261287 166-176.indd 168 30/05/14 18:00

171. 169
9
Contagens visuais.
Traduzir contagens visuais por expressões numéricas
1. Observa as bolas de ténis. Quantas são?
Regularidades
a)
Observando as imagens iguais a esta, descobre diferentes modos de contar as bolas
de ténis e escreve as respetivas expressões numéricas.
b)
Se ainda não encontraste, no arranjo de bolas de ténis, uma forma de contagem
correspondente à expressão numérica (3 3 5) 1 (2 3 4) 1 (2 3 1), tenta encontrá-la.
2. Encontra uma expressão numérica que represente o número de azulejos brancos.
Eu posso contar
utilizando a expressão
numérica:
(4 3 4) 1 (3 3 3)
3. Observa as flores no canteiro.
a) Quantas flores tem o canteiro?
b)
Escreve expressões numéricas
que traduzam diferentes formas
de contar.
261287 166-176.indd 169 30/05/14 18:00

172. 170
Padrões de repetição
1.
No teu caderno, repete o motivo formado por este grupo de figuras até teres, ao todo,
15 figuras.
Quais são os polígonos do motivo?
De acordo com a regra de formação definida, responde às questões seguintes.
a)
Quantas vezes precisarás de desenhar o motivo para obteres 6 hexágonos?
b)
Quantas vezes precisarás de desenhar o motivo para obteres 12 triângulos?
c)
Para conseguires organizar melhor o teu raciocínio, completa a tabela.
Número de cópias
do motivo
Número
de hexágonos
Número
de triângulos
Número
de polígonos
1 1 2 3
4
3
12
20
42
25
2.
Observa com atenção a tabela que completaste e relaciona os números em cada linha.
Completa agora a tabela seguinte.
Número de cópias
do motivo
Número
de hexágonos
Número
de triângulos
Número
de polígonos
n 2 3 n
a)
Qual é o polígono que fica na 30.ª posição? Explica como chegaste a essa conclusão.
b)
Quantas cópias do motivo tem uma sequência com 150 hexágonos?
Explica como pensaste.
c)
Imagina que tínhamos uma sequência com 300 polígonos. Nessa sequência,
quantos hexágonos haveria? E triângulos?
Regularidades
261287 166-176.indd 170 30/05/14 18:00

173. 171
9
3.
Na escola da Marta, costumam organizar a festa da Gala da Primavera no Auditório
Municipal. Para fazer um friso no auditório onde se realizou a Gala da Primavera,
utilizaram-se grupos de duas margaridas, uma rosa e uma túlipa.
Sabendo que precisaram de 280 grupos como este, diz de quantas margaridas, rosas e
túlipas necessitaram. Explica como chegaste à tua resposta.
DESAFIO As flores do auditório
As margaridas estão na 1.ª e 2.ª posições, a rosa na 3.ª posição e a túlipa na 4.ª
posição. Continuando a sequência, diz qual é a flor que ficará na 12.ª, 20.ª, 35.ª
e na 100.ª posições. Explica o teu raciocínio.
A primeira túlipa da sequência está na 4.ª posição. Continuando a sequência, em
que posições vais encontrar túlipas?
4.
Observa a seguinte sequência, em que se repetem sucessivamente os objectos: caderno, cola,
caderno, lápis, por esta ordem. De acordo com esta regra responde às questões seguintes.
a)
Em que posições estão os cadernos?
b)
Poderá um caderno estar na 14.ª posição? Explica a tua resposta.
c)
Regista as posições dos tubos de cola. Encontras alguma regularidade?
d)
Substitui cada objeto por uma letra e cria um padrão de repetição até teres 20 letras.
e) Utilizando as imagens deste padrão (caderno, lápis, cola), constrói padrões do tipo:
A A B C
A B C A
Regularidades
261287 166-176.indd 171 30/05/14 18:00

174. investiga Mais palhinhas
Qual é o número de palhinhas necessário para construir um «comboio» formado por
10 quadrados encostados lado a lado?
Será que conseguimos saber o número de palhinhas necessário para a construção
de um «comboio» com qualquer número de quadrados?
172
Padrões de crescimento
1.
Observa a sequência seguinte, construída com palhinhas de igual comprimento.
Os termos de ordem par obtêm-se justapondo um triângulo na posição indicada a azul,
e os termos de ordem ímpar obtêm-se justapondo um triângulo na posição indicada
a vermelho. De acordo com esta regra, responde às questões seguintes.
2. Observa a sequência e determina uma possível regra de formação.
a)
Determina o número de palhinhas, o número de triângulos e o perímetro (considera
o tamanho da palhinha como a unidade) para os «comboios» 4, 5, 6, 7, 8 e 9.
Para organizares o teu raciocínio, podes utilizar uma tabela como a seguinte.
Número do «comboio» 1 2 3
Número de triângulos
Número de palhinhas
Perímetro
b)
Determina o perímetro de um «comboio» com 20 triângulos. Como chegaste a esse
resultado?
a)
Desenha a 4.ª figura da sequência e explica como pensaste para a construir.
b)
Indica, sem construíres as figuras, quantos quadrados serão necessários para
construir a 5.ª e a 6.ª figuras, de acordo com essa regra. Explica como pensaste.
Regularidades
«Comboio» 1 «Comboio» 2 «Comboio» 3
A B C
261287 166-176.indd 172 30/05/14 18:00

175. 173
9
DESAFIO Os pátios
O Sr. Sebastião está a desenhar pátios para uma urbanização. Cada pátio tem uma
área quadrada no centro para jardim. Ele está a utilizar quadrículas castanhas para
representar o jardim e quadrículas brancas para representar os contornos de cada pátio.
As figuras representam os três pátios mais pequenos de uma sequência.
Determina possíveis regras de formação, para calcular o número de quadrículas
brancas e o número de quadrículas castanhas de qualquer pátio.
De acordo com essas regras, quantas quadrículas de cada cor vai o Sr. Sebastião usar
para desenhar o pátio n.º 5?
Se utilizares 36 quadrículas castanhas, quantas quadrículas brancas terás de usar?
Regularidades
Pátio 1 Pátio 2 Pátio 3
3.
Observa a sequência e determina uma possível regra de formação. De acordo com essa
regra, responde, no teu caderno, às seguintes questões.
a)
Tomando como unidade de medida a área de um quadrado, indica a área de cada
uma das figuras.
b) Descobre uma forma de saberes a área da 10.ª figura sem a desenhares.
Discute-a com os teus colegas.
4.
O Pedro e o Diogo estiveram a fazer construções com tampas de garrafas, formando
uma sequência. Determina uma possível regra de formação e, de acordo com essa regra,
responde no teu caderno, às questões seguintes.
a)
Conta o número de tampas de cada
uma das figuras e indica o número
de tampas necessário para eles
construírem a 4.ª e a 5.ª figuras.
b)
Explica a sequência de números
que obténs.
C
B
A
Fig. 4
Fig. 3
Fig. 2
Fig. 1
261287 166-176.indd 173 30/05/14 18:00

176. 174
REVISÃO
1.
Na tabela dos 100 números apresentada, há números que estão pintados.
a) Encontra uma regularidade nos números que estão pintados e descreve-a.
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
34 40
30
b)
Colorindo tabelas de 100 números, descreve os padrões que encontras, seguindo
as regras de construção apresentadas.
Regras de construção:
Números com um 7.
Números que são múltiplos de 5.
Números que têm os dígitos iguais.
Números que são divisíveis por 2.
Números cuja soma dos algarismos é 9.
2.
Na tabela apresentada ao lado, descobre
uma possível regularidade e completa-a
de acordo com essa regularidade.
3.
Para cada sequência, determina uma possível regra de formação e, de acordo com essa
regra, escreve os três números seguintes.
a) 14 — 19 — 24 — 29 b) 15 — 18 — 20 — 23 — 25 — 28
261287 166-176.indd 174 30/05/14 18:00

177. 175
9
4.
A sequência seguinte obtém-se pela repetição das figuras «boné, esfera, estrela», por
esta ordem.
Qual é a tarefa em que sentiste mais dificuldade? Porquê?
Qual é a tarefa em que sentiste menos dificuldade? Porquê?
Autoavaliação
a)
De acordo com essa regra, desenha as figuras a colocar em cada espaço.
b) Com estas figuras, define uma nova sequência e descreve a sua regra de formação.
5.
Observa a sequência e determina uma possível regra de formação. De acordo com essa
regra, responde, no teu caderno, às questões seguintes.
a) Descreve o processo de construção de cada um dos termos.
b) Constrói o 4.º e o 5.º termos.
c) Achas que poderá haver algum termo com 50 bolinhas? Porquê?
4.
Observa as três primeiras figuras de uma sequência e determina uma possível regra de
formação. De acordo com essa regra, responde, no teu caderno, às seguintes questões.
a)
De quantos quadrados necessitaste para construir cada uma das figuras?
b) Desenha a 4.ª figura.
c)
Consegues prever quantos quadrados são necessários para construíres a 6.ª figura?
Explica como pensaste.
261287 166-176.indd 175 30/05/14 18:00

178. 176
Autoavaliação
Regista nesta grelha a tua autoavaliação.
Sugestão: Muitas vezes Algumas vezes Poucas vezes
Itens 1.º P. 2.º P. 3.º P.
Fui assíduo e pontual.
Mantive o meu material organizado e com boa
apresentação.
Adquiri métodos de trabalho.
Cooperei no trabalho em equipa.
Revelei espírito de entreajuda.
Aceitei opiniões e estratégias diferentes das minhas.
Discuti com o grupo estratégias e resultados.
Comuniquei à turma ideias matemáticas.
Compreendi e apliquei novas aprendizagens.
Desenvolvi o meu cálculo mental.
Compreendi quais os dados importantes para a resolução
de problemas.
Usei estratégias adequadas na resolução de problemas.
Desenvolvi o meu raciocínio na resolução de problemas.
Partilhei com a turma os meus raciocínios
e as minhas estratégias.
261287 166-176.indd 176 30/05/14 18:00