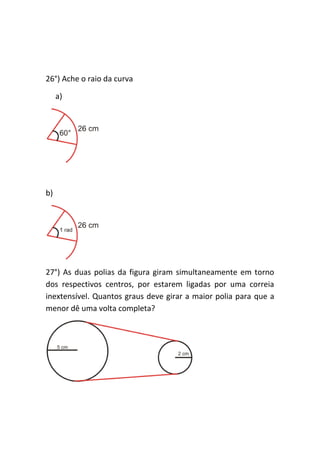
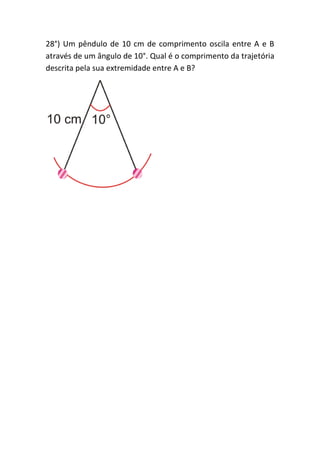
Este documento apresenta uma lista de exercícios sobre trigonometria, incluindo a conversão entre graus e radianos, cálculo de comprimentos de arcos e ângulos centrais de circunferências. Os exercícios envolvem tópicos como relação entre arco e ângulo central, cálculo de comprimentos de arcos, conversão entre sistemas de medida de ângulos e problemas geométricos envolvendo circunferências.

1. Trigonometria
Lista de Exercícios 01
1°) Transforme 225° em radianos.
2°) Transforme em radianos:
a) 210°
b) 270°
c) 315°
d) 240°
e) 300°
f) 330°
3°) Transforme em graus.
4°) A seguir temos medidas de arcos em radianos, transforme-os
em graus.
a)
b)
c)
d)
e)
f)

2. g)
h)
i)
j)
5°) Um arco de circunferência mede 40 cm e o raio de
circunferência mede 5 cm. Calcular a medida do arco em
radianos.
6°)
7°) Um grau se divide em 60’ (60 minutos) e um minuto se divide
em 60’’ ( 60 segundos). Por exemplo, um arco de medida 30’ é
um arco de 0,5°. Transforme em radianos o seguintes arcos:
a) 22°30’
b) 41°10’21’’
8°) Converta em graus o arco 1 rad.

3. 9°) Escreva em radianos as medidas dos arcos x e y tais que
x – y = 15° e x + y = rad.
10°) Escreva em graus as medidas dos arcos x, y e z tais que
x + y + z = 13°, x + y + 2z = e x + 2y + z =
Nos exercícios que seguem adote , quando for
necessário.
11°) Seja 10 cm o raio de uma circunferência. Calcule seu
comprimento.
12°)
13°) Uma circunferência tem perímetro de 100 m. Determine seu
raio.
14°) Exprima em radianos
a) 30°
b) 45°
c) 60°
d) 90°

4. e) 15°
f) 75°
g) 225°
h) 300°
i) 240°
15°) Escreva os valores dos arcos abaixo em graus
a)
b)
c)
d)
e)
16°) Coloque em ordem crescente os ângulos abaixo:
, 50°, , , 90°
17°) Nos casos apresentados abaixo, determine o comprimento
aproximado de um arco de , tomado de uma circunferência
de raio:

5. 18°) Em cada caso, determine o comprimento aproximado de
um arco de 45°, tomado sobre uma circunferência de raio:
a) 1 m
b) 2 m
c) 0,4 m
d) 11 m
e) 5 m
19°)
20°) Calcule o ângulo entre os ponteiros do relógio às 4 horas e
20 minutos.
21°) Calcule, em cada caso, o menor ângulo formado entre os
dois ponteiros de um relógio que marca:
a) 4h 10 min
b) 2h 50 min
22°) Na figura, qual o percurso mais curto sobre as
semicircunferências: AMB ou ADCEB?

6. 23°) São dados dois arcos: o primeiro, α, de medida rad,
tomado sobre uma circunferência de 3 cm de raio; o segundo, β,
de medida 60°, em uma circunferência de 4 cm de raio. Compare
os respectivos comprimentos e .
24°) Escreva em graus e em radianos as medidas dos ângulos
centrais formados na figura abaixo.
25°) Uma moto percorre 78,5 m de uma curva, descrevendo arco
de 45°. Determine o raio da curva.

7. 26°) Ache o raio da curva
a)
b)
27°) As duas polias da figura giram simultaneamente em torno
dos respectivos centros, por estarem ligadas por uma correia
inextensível. Quantos graus deve girar a maior polia para que a
menor dê uma volta completa?

8. 28°) Um pêndulo de 10 cm de comprimento oscila entre A e B
através de um ângulo de 10°. Qual é o comprimento da trajetória
descrita pela sua extremidade entre A e B?